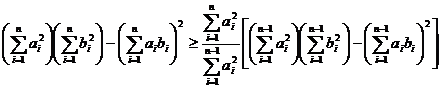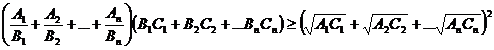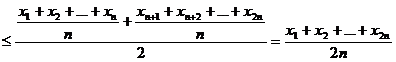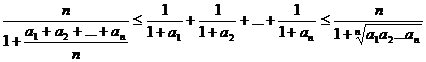Inegalitati - idei
si metode
Cartea prezinta metodele de
baza pentru demonstrarea
inegalitatilor:
- Reducerea
- Substituirea
- Exploatarea trinomului de gradul
doi
- Spargerea
- Folosirea simetriei
- Normarea
- Intercalarea
- Exploatarea ordinii (inegalitati
Cebisev)
- Deconditionarea
- Apelul la identitati
- Reducerea la absurd
- Coborarea
- Inductia
- Metoda Sturm
- Limitele
- Exploatarea monotoniei
- Exploatarea convexitatii
- Cvasi-liniarizarea
- Demonstrarea
inegalitatilor integrale
Voi
prezenta in continuare cateva paragrafe ale cartii care mi s-au
parut mai interesante, desi alegerea a fost foarte greu de
facut.
Capitolul 3. Exploatarea
trinomului de gradul al doilea
Principiul trinomului
Demonstratie a inegalitatii CBS
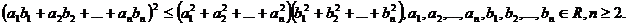 In cazul in care pentru macar un
In cazul in care pentru macar un  avem
avem  , consideram functia de gradul doi cu coeficientul
dominant pozitiv
, consideram functia de gradul doi cu coeficientul
dominant pozitiv
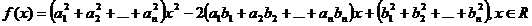
Inegalitatea
CBS este echivalenta cu 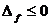 . Pentru demonstrarea ei e suficient sa dovedim ca
. Pentru demonstrarea ei e suficient sa dovedim ca 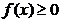 pentru orice
pentru orice 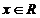 . Observam ca
. Observam ca
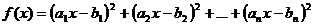 .
.
Pentru
a avea egalitate in CBS, deci pentru a avea 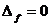 , este obligatoriu sa existe un
, este obligatoriu sa existe un 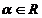 pentru care
pentru care 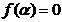 , aceasta insemnand ca sistemul
, aceasta insemnand ca sistemul
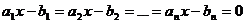 ,
,
cu
singura necunoscuta x, are solutie, adica n-uplele 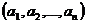 si
si  sunt
proportionale.
sunt
proportionale.
3.5. Apelul la valoarea de extrem
Pentru demonstrarea unor inegalitati putem apela la extremul
functiei de grad doi.
Daca 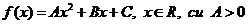 avem
avem
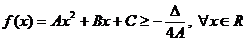
inegalitate
verificata cu egal pentru 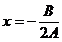 .
.
Fie
inegalitatea
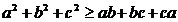 ,
,
punem 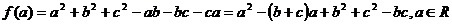 .
.
Cum 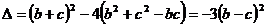 , inegalitatea (*) devine
, inegalitatea (*) devine
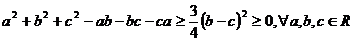
Revenim
la inegalitatea CBS
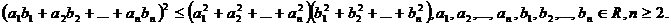 Punem
Punem 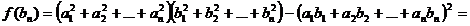
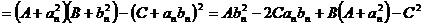 ,
,
unde 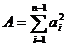 ,
, 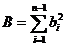 ,
, 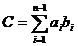 .
.
Cum
A>0 inegalitatea (*) devine
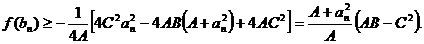
Obtinem
astfel
(**) 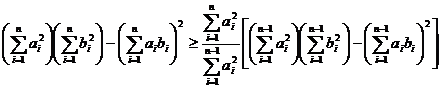
Inegalitate care se poate folosi pentru a demonstra inegalitatea CBS prin
inductie.
Capitolul 7.
Intercalarea
7.7. Trucul CBS
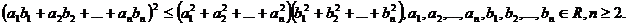 Pentru inegalitati de genul
Pentru inegalitati de genul
(*) 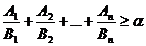 , unde
, unde 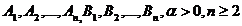 ,
,
putem
incerca o intercalare care foloseste un mic "truc" care consta in
esenta in inmultirea inegalitatii date cu o suma de termeni
pozitivi astfel incat expresia din membrul stang sa fie antrenata
intr-o inegalitate CBS.
Pentru 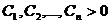 avem, conform CBS,
avem, conform CBS,
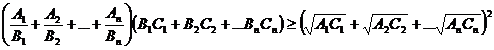
Acum
este suficient sa fie adevarata inegalitatea:
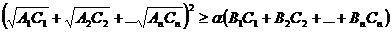
pentru
ca si inegalitatea (*) sa fie adevarata. Deci ( ?) T (*) ceea ce inseamna ca e posibil
ca inegalitatea (*) sa fie adevarata fara ca inegalitatea
( ?) sa fie adevarata. In aceasta consta si
slabiciunea acestei metode. Avantajul ei consta in faptul ca
inegalitatea ( ?) ne scapa de numitorii din (*) si cu o
buna alegere a numerelor  si de radicalii
din ( ?). Morala este ca aceasta schema de intercalare
merita incercata pentru inegalitati ce folosesc numitori
incomozi.
si de radicalii
din ( ?). Morala este ca aceasta schema de intercalare
merita incercata pentru inegalitati ce folosesc numitori
incomozi.
Exemple:
1. 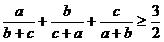 2.
2. 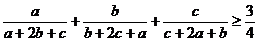 , a,b,c>0
, a,b,c>0
Capitolul 13.
Inductia
13.4 Inductia Cauchy
Principiul
de inductie Cauchy
Fie
P(n) un predicat peste N.
Daca P(2) este adevarata,
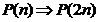 pentru orice
pentru orice 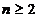 si
si
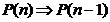 pentru orice
pentru orice 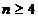
atunci P(n) este adevarata pentru orice 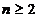 .
.
Avantajul inductiei Cauchy in
comparatie cu inductia standard consta in faptul ca adesea in cazul unei
inegalitati se poate trece mai usor de la cazul n la cazul 2n decat la cazul
n+1. Apoi "coborarea" de la cazul n la cazul n-1 ar trebui sa s efaca relativ
usor, prin particularizare.
Pentru a demonstra inegalitatea
mediilor
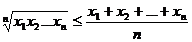
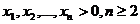 ,
,
prin
inductie Cauchy, consideram predicatul
P(n):
"pentru orice 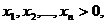
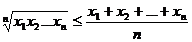 ,
,
inegalitate
verificata cu egal daca si numai daca 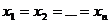 ."
."
P(2) este
adevarata deoarece pentru orice 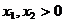 avem
avem
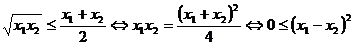 .
.
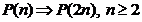
Pentru 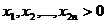 avem
avem
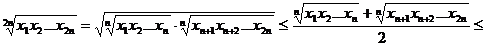
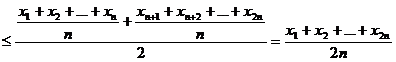
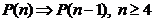
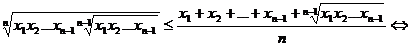
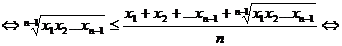
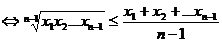
Exemple
- Inegalitatea lui Huygens
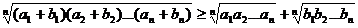 ,
,
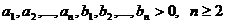
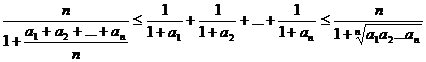
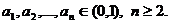
Capitolul 8. Exploatarea ordinii
8.1. Doua teoreme de maximizare
Teorema A. Fie 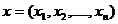 si
si 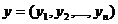 n-uple de numere
reale,
n-uple de numere
reale, 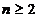
Daca x si y
sunt la fel ordonate, atunci, dintre toate sumele 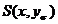 , cea maxima corespunde permutarii identice, adica:
, cea maxima corespunde permutarii identice, adica:
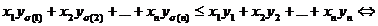
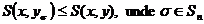
In cazul in
care x si y sunt invers ordonate, atunci, din toate sumele 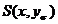 cea minima corespunde
permutarii identice, adica
cea minima corespunde
permutarii identice, adica
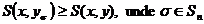
Folosind Teorema A autorul da o foarte frumoasa
demonstratie ("o perla") pentru inegalitatea mediilor
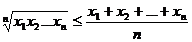
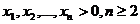
Notam 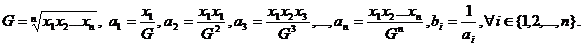
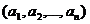 si
si 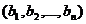 sunt strict invers
ordonate si atunci, din teorema A avem:
sunt strict invers
ordonate si atunci, din teorema A avem:
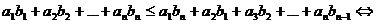
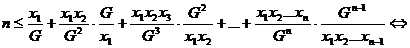
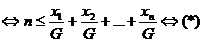
Inegalitarea se verifica cu egal daca si
numai daca
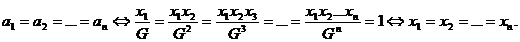
profesor Nicolae Stipeanu