CALCULABILITATE
SI COMPLEXITATE - GRAFURI
Teoria complexitatii
Teoria complexitatii (complexity theory) se ocupa
cu studiul lucrurilor care se pot calcula atunci cand resursele pe care le avem
la dispozitie sunt limitate. Resursele fundamentale in teoria
traditionala erau:
Timpul
disponibil pentru executia unui program;
Spatiul
sau cantitatea de memorie disponibila pentru a stoca date.
dar dezvoltarile mai recente au aratat ca alte
genuri de resurse au un impact foarte important asupra lucrurilor care se pot
calcula, cum ar fi:
Aleatorismul,
sau cantitatea de biti aleatori pe care-i avem la
dispozitie;
Paralelismul,
sau numarul de elemente de procesare care pot opera in
paralel;
Interactiunea,
sau numarul de mesaje schimbate intre doua
entitati care calculeaza;
Sfaturi de la un oracol:
chiar daca nu stim sa rezolvam o anumita
problema, daca presupunem ca cineva vine si ne da
raspunsul, exista apoi in continuare probleme grele?
Dintr-un anumit punct de vedere, teoria complexitatii
este exact opusul teoriei algoritmilor, care probabil partea cea mai
dezvoltata a informaticii teoretice: daca teoria algoritmilor ia o problema
si ofera o solutie a problemei in limitele unor resurse, teoria
complexitatii incearca sa arate cand resursele sunt insuficiente
pentru a rezolva o anumita problema. Teoria complexitatii
ofera astfel demonstratii ca anumite lucruri nu pot fi
facute, pe cand teoria algoritmilor arata cum lucrurile pot fi
facute.
De exemplu, atunci cand invatam un algoritm de
sortare ca quicksort, demonstram ca problema sortarii a n
numere se poate rezolva in timp proportional cu n log n.
Stim deci ca sortarea se poate face in timp cel mult n log n,
sau mai putin.
Pe de alta parte, teoria complexitatii ne
arata ca pentru a sorta n numere oarecare ne trebuie cel
putin timp n log n, si ca este imposibil
sa sortam mai repede, daca nu avem informatii suplimentare
despre valorile de sortat.
Combinand aceste doua rezultate, deducem ca problema
sortarii are complexitatea exact n log n, pentru ca:
Avem un algoritm de timp n log n;
Am demonstrat ca nu se poate mai bine de atat.
Aceasta stare de fapt este una extrem de fericita,
si din pacate foarte rara: pentru majoritatea problemelor pe
care le cunoastem, exista o distanta mare intre cea mai
buna posibilitate de rezolvare pe care o cunoastem si limita
inferioara cea mai ridicata pe care o putem demonstra. Situatia
este ca in figura 1.
|
|
|
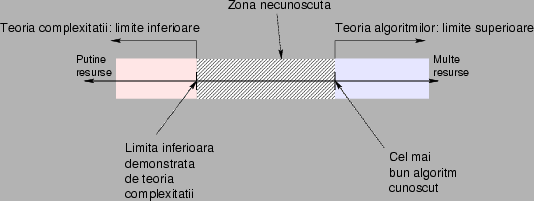
Figura 1: Existenta unui algoritm pentru a
rezolva o problema ofera o limita superioara pentru
complexitatea problemei: in regiunea albastra, din dreapta, putem
rezolva problema. Teoria complexitatii gaseste limite
inferioare: daca ne plasam in regiunea rosie, cu certitudine
problema este insolvabila. Foarte adesea, intre cele doua regiuni
exista o zona (hasurata cu negru) despre care nu putem
spune nimic. Din pacate, aceasta zona este adesea foarte mare
ca intindere.
|
Chiar pentru probleme aparent banale, complexitatea minima
este adesea necunoscuta. De exemplu, algoritmul cel mai bun cunoscut
pentru a inmulti doua numere de n cifre are complexitatea n
log log n, dar limita inferioara oferita de teoria
complexitatii este de n. Algoritmul invatat in
scoala primara pentru inmultire are complexitatea n2.
Nimeni nu stie cat de jos poate fi impinsa aceasta limita,
dar teoria complexitatii ne garanteaza ca nu mai jos de n
(de fapt in cazul de fata nu e nevoie de nici o teorie pentru a ne
spune asta: in timp mai putin de n nu poti nici macar
sa citesti toate cifrele numerelor de inmultit).
Pentru foarte multe probleme importante, distanta intre limitele
inferioara si superioara cunoscute este enorma: de exemplu
pentru problema satisfiabilitatii, careia i-am consacrat
ultimele mele doua articole, limita superioara este o functie
exponentiala (2n) iar cea inferioara este una
polinomiala (nk), pentru un k constant, independent de
problema.
Intr-un anume sens, teoria complexitatii are o
sarcina mult mai grea decat cea a algoritmilor: teoria algoritmilor
demonstreaza propozitii de genul: "exista un algoritm de
complexitate n log n care inmulteste doua numere".
Acest lucru este de obicei facut chiar construind acel algoritm. Pe de
alta parte, teoria complexitatii trebuie sa demonstreze
teoreme de genul "Nu exista nici un algoritm care rezolva
aceasta problema in mai putin de n log n pasi".
Ori asa ceva este nu se poate demonstra in mod direct: exista un
numar infinit de algoritmi, deci nu putem pur si simplu sa-i
verificam pe toti.
Modele de calcul si resurse
Am tot mentionat tot felul de limite (ex. n2), dar
nu am spus ce inseamna acestea. Atat teoria complexitatii, cat
si teoria algoritmilor, masoara complexitatea in acelasi
fel, si anume asimptotic. Asta inseamna ca
masuram numarul de operatii facute ca o functie
de cantitatea de date care ne este oferita spre prelucrare, si
ca impingem aceasta cantitate spre infinit. Atunci complexitatea este
exprimata ca o functie pe multimea numerelor naturale: pentru
fiecare marime de intrare, avem o complexitate. Daca putem avea mai
multe date de intrare cu aceeasi marime (de exemplu, cand sortam
putem avea mai multi vectori de lungime n), atunci complexitatea
pentru intrarea n este luata ca fiind maximumul dintre toate
valorile: max(|i|=n) f(i), unde f este complexitatea si
i sunt datele de intrare (simbolul | | reprezinta marimea
datelor).
Decidabilitate
Un loc aparte in studiul complexitatii il au
masinile care dau totdeauna un raspuns "da" sau "nu". Cu alte
cuvinte, limbajul de iesire are doar doua elemente. Spunem despre
astfel de masini ca decid un limbaj: limbajul decis este
format din cuvintele de la intrare pentru care masina raspunde "da". Toate
problemele pentru care asteptam un raspuns "da" sau "nu" se
numesc ca atare probleme de decizie; problema SAT, a
satifiabilitatii, este un exemplu de problema de decizie.
Problemele de decizie sunt o subclasa foarte interesanta
a tuturor problemelor, pentru ca adesea putem enunta orice
problema ca o colectie de probleme de decizie. Aceasta
notiune a fost prezentata in cazut problemei SAT ca "autoreducere".
Ideea este insa destul de simpla.
De exemplu, sa consideram problema "care sunt factorii
primi ai numarului n?". Putem reduce aceasta problema la mai
multe probleme de decizie, care ne dau exact aceeasi informatie: "este
2 un factor prim al lui n", "este 3 " etc. Daca stim
raspunsurile la toate aceste probleme de decizie, putem obtine
raspunsul si la problema initiala.
Masina Turing
Am clarificat cum arata datele; cum masuram
insa resursele consumate? Consumate de fapt de cine?
Ne trebuie un model precis de calcul. Cel mai folosit este un
model propus in anii treizeci de marele matematician englez Alan Turing:
masina Turing. Masina Turing este un calculator redus la esente,
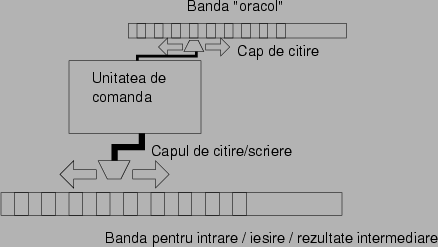
abstractizat. Masina Turing (figura 2) este compusa din
urmatoarele piese:
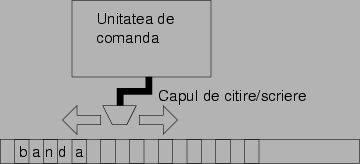
Figura 2: Masina Turing este un model de
calcul abstract propus de matematicianul Alan Turing. Ea consta dintr-o
banda infinita, pe care pot fi scrise simboluri, un cap de
scriere-citire, care poate fi plimbat pe suprafata benzii, si o
unitate de control, care cuprinde un numar finit de reguli care
indica masinii ce sa faca la fiecare miscare in
functie de litera curenta de pe banda si starea in care masina
se afla. In pofida simplitatii ei, masina Turing poate
calcula orice poate fi calculat cu cele mai performante supercomputere.
O banda infinita de hartie cu
patratele; in fiecare patratel se poate scrie
exact un caracter din alfabetul nostru; banda este initial plina cu "spatii",
mai putin partea de la inceput, unde este scris sirul cu datele de
intrare;
Un cap de citire-scriere, care se poate misca deasupra
benzii, la stanga sau la dreapta;
O unitate de control, care contine un numar finit de
reguli. Unitatea de control este la fiecare moment dat intr-o stare;
starile posibile sunt fixate dinainte, si sunt in numar finit.
Fiecare regula are forma urmatoare:
Daca
sunt in starea Q1;
sub capul de citire este litera X;
atunci:
trec in starea Q2;
scriu pe banda litera Y;
mut capul de citire/scriere in directia D.
Si asta-i tot! Un algoritm de calcul este descris de o astfel
de masina, prin toate starile posibile, si toate aceste
reguli, numite reguli de tranzitie, care indica cum se trece
de la o stare la alta.
Orice alte modele de calcul care au fost propuse de-a lungul
timpului, au fost dovedite a fi mai putin expresive, sau tot atat de
expresive cat masina Turing. Nimeni nu a fost in stare, pana acum,
sa zica: "eu cred ca de fapt masina Turing e prea
limitata; iata care zic eu ca sunt operatiile elementare pe
care le avem la dispozitie, din care ar trebui sa exprimam orice
algoritm", si sa ofere ceva care sa fie construibil, si
care sa poata face lucruri pe care masina Turing nu le poate
face.
Din cauza asta logicianul Alonzo Church a emis ipoteza ca
masina Turing este modelul cel mai general de calcul care poate fi propus;
acest enunt, care nu este demonstrabil in sens matematic, se numeste "Teza
lui Church". Acesta este un postulat asupra caruia trebuie sa
cadem de acord inainte de a putea conversa orice lucru privitor la teoria
complexitatii.
Daca avem un model de calcul, putem defini foarte precis ce
intelegem prin complexitate:
Timpul de calcul
pentru un sir dat la intrare, este numarul de
mutari facut de masina Turing inainte de a intra in starea "terminat";
Spatiul
consumat pentru un sir de intrare, este numarul de
casute de pe banda pe care algoritmul le foloseste in
timpul executiei sale.
Clase de complexitate robuste
Cand spun ca masina Turing este la fel de puternica
ca orice alt model de calcul, nu inseamna ca poate calcula la fel de
repede ca orice alt model de calcul, ci ca poate calcula aceleasi
lucruri.
Putem sa ne imaginam tot felul de modificari minore
ale masinii Turing, care o vor face sa poata rezolva anumite
probleme mai repede. De exemplu, putem sa ne imaginam ca
masina are dreptul sa mute capul la orice casuta
dintr-o singura miscare, fara sa aiba nevoie
sa mearga pas cu pas; atunci banda s-ar comporta mai
asemanator cu o memorie RAM obisnuita.
Atunci cum de putem discuta despre complexitate, daca timpul
de rezolvare depinde de modelul de executie?
Aici teoria complexitatii se desparte de teoria
algoritmilor; teoria algoritmilor foloseste de regula modelul RAM
pentru a evalua complexitatea unui algoritm. Teoria complexitatii
face niste diviziuni mai grosolane.
Si anume, exista niste clase de complexitate care
sunt complet invariante la variatele definitii ale masinii Turing:
ca are doua capete de acces la banda, ca poate sari
oriunde, complexitatea ramane aceeasi. O astfel de clasa de
complexitate este clasa tuturor problemelor care se pot rezolva in timp
polinomial, o alta este cea a tuturor problemelor care se pot rezolva in
spatiu polinomial etc. Aceste clase de complexitate sunt numite "robuste",
pentru ca definitia lor nu depinde de modelul de masina.
Acest lucru se poate demonstra aratand ca o masina de un
anumit model poate simula pe cele diferite fara a cheltui prea multe
resurse suplimentare.
Teoria complexitatii mai decreteaza si ca
toate problemele care se pot rezolva in timp polinomial sunt rezolvabile, iar
toate cele care au nevoie de mai mult timp sunt intractabile. Aceasta
definitie este in general adevarata din punct de vedere practic,
dar trebuie luata cu un graunte de sare: cateodata un algoritm n3
este inacceptabil, daca problema este prea mare, altadata unul
de timp chiar exponential este tolerabil, daca masina cu care-l
rulam este foarte rapida. Din punct de vedere teoretic,
separatia insa este perfect acceptabila, pentru ca
intotdeauna ne gandim la probleme pentru care marimea datelor de intrare
tinde spre infinit.
As vrea sa mai fac o observatie foarte
importanta: o problema este foarte strans legata de limbajul in
care o exprimam. Iata un exemplu: sa consideram problema
inmultirii a doua numere. Daca limbajul in care lucram
exprima numerele in baza 2 (sau orice alta baza mai mare de 2),
atunci se cunosc algoritmi de complexitate n log n pentru a face
inmultirea. Pe de alta parte, daca insistam sa scriem
numerele in baza 1 (adica numarul 5 este reprezentat de cinci "betisoare",
ca la clasa I), atunci, in mod evident, complexitatea inmultirii a
doua numere de lungime totala n este n2: chiar rezultatul
inmultirii lui n cu n este scris cu n2 betisoare,
deci nu are cum sa ne ia mai putin timp, pentru ca trebuie
sa scriem rezultatul!
Si mai spectaculoasa este diferenta pentru
algoritmul care verifica daca un numar este prim: daca
limbajul de intrare exprima numerele in baza 2, cel mai bun algoritm
cunoscut are complexitatea 2n, exponentiala, dar daca
scriem numerele in baza 1, complexitatea este n2. Acest lucru se intampla
pentru ca un numar scris in baza 1 este mult mai lung decat scris in
baza 2 n este scris in baza 2 cu log n cifre).
calculabilitate
O intrebare pe care un matematician si-o pune imediat este:
are vreo importanta cate resurse dam unei masini Turing? Nu
cumva totul se poate calcula cu aceeasi cantitate de resurse?
Exista niste teoreme deosebit de interesante din acest
punct de vedere. O teorema arata ca daca dam unei
masini mai mult timp (sau spatiu), atunci ea poate efectua lucruri pe
care nici una din masinile care au mai putin timp nu le poate
efectua. Aceasta teorema se numeste "teorema gaurii" (gap
theorem), pentru ca arata ca intre feluritele clase de
complexitate exista diferente: clasa limbajelor care se pot decide in
timp n3 este diferita de clasa limbajelor care se pot decide in
timp n4.
Enuntul teoremei este de fapt destul de incalcit, si se
bazeaza pe niste detalii tehnice, pe care o sa le trec sub
tacere. Demonstratia este insa relativ simpla, si se
bazeaza pe o tehnica ades folosita in teoria
complexitatii, numita diagonalizare. Aceasta
tehnica a fost folosita in demonstratia lui Cantor, pentru a
arata ca numerele reale nu sunt numarabile.
Ideea de baza este urmatoarea: masina cu mai multe
resurse isi poate permite sa faca orice face masina cu mai
putine resurse, iar dupa aceea sa mai si prelucreze
rezultatul. Cu alte cuvinte, putem construi o masina cu resurse mai
multe, care da un rezultat diferit de orice masina mai
simpla. Rezulta ca masina cu mai multe resurse calculeaza o
functie diferita de toate celelalte!
Numerabilitate
Teorema gaurii se bazeaza in mod explicit pe faptul
ca nu exista prea multe masini Turing! Din moment ce fiecare
masina Turing poate fi descrisa printr-un sir de caractere
finit, inseamna ca putem enumera toate masinile Turing.
Exista astfel un numar numarabil de masini Turing (deci cu
mult mai putine decat exista numere reale!).
O consecinta interesanta a acestui fapt este
ca calculatoarele nu pot manipula numerele reale. Exista mai
multe numere reale decat algoritmi posibili! Limbajele care opereaza cu
numere reale, de fapt manipuleaza niste aproximari cu cateva
zeci sau zecimale ale acestora. Nu putem face mai bine de atat nici daca
operam cu reprezentari simbolice ale numerelor reale (vom putea
manipula unele numere reale, dar nu pe toate; vor exista intotdeauna
operatii cu numere reale care nu sunt calculabile).
Exista si alte consecinte interesante ale acestui
fapt. De exemplu, pute privi masinile Turing ca pe niste aparate care
calculeaza functii de la numerele naturale (N) la N. Ei bine,
exista 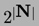 astfel
de functii, adica puterea continuului (adica tot atatea cat numere
reale). Dar masinile Turing sunt doar in numar de
astfel
de functii, adica puterea continuului (adica tot atatea cat numere
reale). Dar masinile Turing sunt doar in numar de  ,
deci mult mai putine. Asta inseamna ca exista o
sumedenie de functii N
,
deci mult mai putine. Asta inseamna ca exista o
sumedenie de functii N 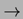 N
care nu se pot calcula cu calculatoarele!
N
care nu se pot calcula cu calculatoarele!
Ce daca, veti spune, poate toate functiile care ne
intereseaza in practica se pot de fapt calcula. Vom vedea de fapt
ca exista functii extrem de importante care nu sunt
calculabile, oricat de multe resurse am pune la bataie!
Semi-decidabilitate
Dupa cum am vazut, exista probleme pentru care nu
putem niciodata calcula raspunsul.
Putem insa identifica printre problemele indecidabile o
submultime, a problemelor semi-decidabile, acele probleme pentru care
putem calcula "jumatate" de raspuns: putem raspunde intotdeauna
corect cand suntem intrebati de o instanta "da", dar cand suntem
intrebati de o instanta "nu" s-ar putea sa dam
raspunsul corect, sau s-ar putea sa nu terminam niciodata
de calculat.
Problema opririi este de fapt o problema semi-decidabila:
daca ni se da o masina M si un sir x pentru care
masina se opreste, vom fi capabili sa descoperim acest lucru simuland
functionarea masinii M cu intrarea x pana atinge starea
finala. Daca M insa nu se opreste cand primeste pe x,
nici simularea nu se va termina niciodata.
Oracole
O intrebare interesanta este urmatoarea: sunt tot felul
de probleme indecidabile; dar sunt cumva unele dintre ele mai grele decat
altele? Poate sa para ciudat ca intrebam astfel de lucruri
despre probleme pe care oricum nu le putem rezolva, dar raspunsul este
si mai surprinzator.
Contextul matematic pentru a formula aceste intrebari este
numit al "oracolelor". Putem gasi o interpretare filozofica
interesanta pentru acest gen de constructii: sa zicem ca
facem un pact cu diavolul, care ne va raspunde corect la anumite
intrebari nedecidabile. De pilda, ne va da intotdeauna raspunsul
corect la intrebari despre oprirea unei masini Turing. Vedeti,
raspunsul exista, orice masina fie se
opreste, fie nu se opreste, ceea ce nu exista este o metoda
de a calcula raspunsul. Sa zicem ca Mefistofel
insa ne poate da raspunsul, folosind puterile sale supranaturale.
Vom vedea ca notiunea de oracol este foarte utila
nu numai atunci cand vrem raspunsuri la intrebari nedecidabile, ci
si atunci cand vrem raspunsuri la intrebari pentru care nu avem
destule resurse. Mai multe despre asta in partea a doua a acestui articol, in
numarul viitor al revistei.
Matematic, un oracol este o a doua banda pentru masina
noastra, pe care sunt scrise dinainte raspunsurile (corecte!) la
intrebarile pe care masina le pune (vedeti figura 4).
Figura
4:
Masini cu Oracole: un oracol este o anumita functie pe care
masina nu o poate calcula, dar de care se poate folosi. Matematic
modelam oracolul printr-o banda infinita, pe care sunt dinainte
scrise raspunsurile corecte la toate intrebarile pe care masina
le-ar putea pune. In general ne intereseaza sa vedem ce ar putea face
in mod suplimentar o masina Turing daca ar putea raspunde unor
anumite intrebari (dar nu oricarei intrebari); atunci o
echipam cu un oracol care stie toate raspunsurile la
intrebarile in chestiune.
Ierarhia
aritmetica
Daca avem un oracol, mai exista lucruri pe care nu le
putem calcula? Exista alte intrebari la care nu putem raspunde?
Ei bine, da. Exista intrebari care sunt in continuare
ne-decidabile. De exemplu, intrebarea "este limbajul acceptat de masina M
finit" nu poate fi elucidata nici in prezenta unui oracol pentru
problema opririi.
Dar daca presupunem ca avem un oracol care ne
raspunde si la aceasta intrebare? Mai exista si
altceva care nu se poate calcula? Din nou, raspunsul este "da": de exemplu
nu putem raspunde nici acum la intrebarea "este limbajul acceptat de
masina M co-finit" (adica sirurile ne-acceptate sunt in
numar finit).
Si asa mai departe: exista o ierarhie infinita
masini de oracole din ce in ce mai puternice, care pot raspunde la
aceste intrebari, dar care sunt neputincioase in fata unor
intrebari mai complicate. Aceasta ierarhie de probleme ne-decidabile
se numeste ierarhia aritmetica.
Teoria clasica a
complexitatii
Voi reaminti ca teoria complexitatii discuta
despre ceea ce se poate calcula si nu se poate calcula atunci cand avem
anumite resurse la dispozitie. Teoria calculabilitatii
discuta cazul extrem al lucrurilor care nu se pot calcula deloc, chiar
daca avem la dispozitie o cantitate infinita de resurse. In mod
surprinzator, exista foarte multe lucruri care nu se pot calcula,
asa cum am aratat in articolul anterior.
Pentru a putea discuta precis despre ce se poate calcula, teoria
complexitatii opereaza cu niste modele matematice ale
masinilor de calcul, descrise sub forma unor automate simple, care
comunica cu lumea exterioara folosind niste benzi pe care sunt
scrise litere, si care au o unitate de control cu un numar finit de
reguli, care indica automatului care este pasul urmator de facut
in fiecare circumstanta.
Modelul cel mai ades folosit este cel al masinii Turing,
numite in cinstea marelui matematician englez, Alan Turing. Turing a fost unul
dintre pionierii acestei teorii; el este insa mai cunoscut prin activitatea
lui din al doilea razboi mondial, cand a contribuit la spargerea
cifrurilor masinii Enigma, care cripta comunicatiile Germaniei
naziste. Munca lui Turing a permis aliatilor sa intercepteze
informatii foarte importante despre miscarile masinii de razboi
germane.
Turing era un matematician de exceptie, care studiase la
Princeton cu Albert Einstein, si colaborase cu John von Neumann,
parintele american al calculatoarelor. In cinstea sa, cel mai important
premiu care recunoaste contributiile in domeniul informaticii,
decernat anual de prestigioasa asociatie ACM (Association for Computing
Machinery), este numit premiul Turing.
In mod interesant, desi masina Turing este un mecanism
foarte "primitiv", nimeni nu a reusit sa sugereze un model de calcul
mai puternic. In masura in care functionarea neuronilor din creierul
uman este cea descrisa de neurofiziologi, creierul insusi poate fi
simulat cu o masina Turing (dar exista mult mai multe
necunoscute decat certitudini in ceea ce priveste functionarea
creierului). Daca acceptam aceasta ipoteza (numita
si teza lui Church), putem privi rezultatele teoriei
complexitatii ca pe niste reguli universale, care privesc toate "aparatele"
care proceseaza informatie in univers.
Sa ne mai amintim ca obiectele procesate de masinile
Turing sunt limbaje, adica multimi de cuvinte. O masina
Turing primeste la intrare un cuvant dintr-un anumit limbaj, si
produce la iesire un cuvant dintr-un alt limbaj, care este raspunsul
asteptat. Daca raspunsurile sunt doar "da" sau "nu" (adica
un singur bit), atunci spunem ca masina Turing decide limbajul format
din toate cuvintele pentru care raspunsul este "da".
Putem considera ca parinte al teoriei complexitatii
pe marele matematician german David Hilbert (1862 - 1943). Hilbert a incercat sa
fundamenteze matematica pe baze axiomatice; el a recunoscut faptul ca
intre logica si matematica exista o relatie foarte stransa;
el a observat ca demonstrarea oricarei probleme din matematica
se poate reduce la verificarea satisfiabilitatii unei formule din
calculul predicativ.
Hilbert vedea ca incununare a matematicii producerea unui algoritm
care ar putea sa rezolve problema satisfiabilitatii, care ar
putea fi atunci folosit pentru a demonstra in mod mecanic orice teorema.
Teorema lui Gödel si teorema lui
Turing
Visele lui Hilbert au fost insa spulberate de matematicianul
Kurt Gödel si faimoasa sa teorema de incompletitudine. Gödel a
aratat ca un algoritm de decizie pentru satisfiabilitate nu
exista, pentru orice sistem axiomatic care este suficient de
cuprinzator pentru a descrie multimea numerelor naturale si
operatiile aritmetice pe ea. Daca operam cu structuri mai
simple, ca algebra booleana, introdusa in articolul nostru despre
satisfiabilitate, problema este decidabila; daca insa structura
matematica este suficient de bogata, (si multimea numerelor
naturale este in definitiv o structura foarte simpla, fara
de care cu greu putem vorbi de matematica evoluata), exista
propozitii adevarate care nu pot fi demonstrate matematic.
O alta problema fundamentala, propusa de
Hilbert, era de a verifica daca un sistem dat de axiome este consistent
sau nu (cu alte cuvinte, daca axiomele nu se contrazic intre ele). De
exemplu, stim din liceu ca axioma paralelelor a lui Euclid, din
geometria plana, este independenta de celelalte axiome ale
geometriei, si ca putem construi geometrii in care aceasta
axioma este adevarata, precum si geometrii perfect coerente
in care axioma este falsa. Hilbert isi dorea posibilitatea de a
verifica daca nu cumva un sistem ales de axiome se contrazice pe sine. A
doua teorema de incompletitudine a lui Gödel a sfarimat si acest
vis al lui Hilbert, demonstrand ca este imposibil de demonstrat
consistenta unui sistem de axiome rationand doar in interiorul
sistemului (cu alte cuvinte, nu putem demonstra consistenta axiomelor
pornind doar de la acele axiome); daca vrem sa facem acest lucru,
trebuie sa rationam intr-un sistem mai cuprinzator decat
cel studiat. Avem astfel o reducere infinita, pentru ca putem pune
apoi chestiunea consistentei sistemului mai cuprinzator etc.
Teorema lui Cook si
NP-completitudinea
Cu timpul oamenii s-au obisnuit cu ideea ca sunt lucruri care
nu se pot calcula. Despre cele care se puteau calcula insa erau
convinsi ca sunt la indemana. Teoria complexitatii
insa a aratat ca fiecare problema are o complexitate
inerenta; anumite probleme se pot rezolva repede, altele mai greu.
Exista probleme care au o complexitate exponentiala: daca
cresti datele de intrare cu o constanta, timpul de calcul se
dubleaza. Astfel de probleme devin foarte repede intractabile: daca
crestem problema de 100 de ori, complexitatea creste de 2100
ori, depasind astfel varsta estimata a universului! Chiar
daca incepeam sa calculam la Big Bang, astazi tot n-am fi
terminat!
Teorema lui Cook, demonstrata in 1971, a turnat si mai
mult gaz peste foc: exista foarte multe probleme care au solutii
simple, si usor de verificat (adica putem verifica foarte
eficient daca o pretinsa solutie este corecta), dar pentru
care nimeni nu stie cum sa gaseasca o solutie
suficient de rapid!
Din acel moment, problema centrala a teoriei
complexitatii s-a mutat in aceasta zona: am renuntat
sa mai rezolvam problemele inerent grele, putem oare macar
rezolva acest gen de probleme, ale caror solutii se pot verifica
usor? Aceste probleme formeaza o clasa numita NP, despre care vom vorbi mai mult in
cuprinsul acestui articol. Intrebarea centrala a teoriei
complexitatii este daca P=NP. (P este clasa problemelor pe care
le putem rezolva rapid.)
S-au publicat mai multe demonstratii eronate ale ambelor
asertiuni: P=NP si P 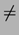 NP. Deocamdata raspunsul ramane
un mister. Teoreticienii au atacat problema din tot felul de perspective, incercand
sa demonstreze ca pentru problemele din NP sunt necesare strict mai multe resurse decat pentru cele din P; atunci am sti ca cele
doua clase sunt diferite. Desigur, doar existenta unei diferente
intre cele doua clase nu este totul pentru practicieni, daca nu
stim si cat de mare este aceasta diferenta. Tot ce
stim este ca NP este
cuprinsa intre P si EXP; P este clasa problemelor cu o complexitate polinomiala, iar EXP cea a problemelor cu complexitate
exponentiala; intre aceste doua clase exista o sumedenie de
clase intermediare, de exemplu cea a problemelor cvasi-polinomiale, care sunt
mai mari decat cele polinomiale, dar mai mici decat cele exponentiale (de
exemplu functia nlog n). Chiar un rezultat care ar separa NP de EXP ar fi grozav, pentru ca ne-ar da solutii pentru
problemele din NP mai bune decat
cunoastem la ora actuala.
NP. Deocamdata raspunsul ramane
un mister. Teoreticienii au atacat problema din tot felul de perspective, incercand
sa demonstreze ca pentru problemele din NP sunt necesare strict mai multe resurse decat pentru cele din P; atunci am sti ca cele
doua clase sunt diferite. Desigur, doar existenta unei diferente
intre cele doua clase nu este totul pentru practicieni, daca nu
stim si cat de mare este aceasta diferenta. Tot ce
stim este ca NP este
cuprinsa intre P si EXP; P este clasa problemelor cu o complexitate polinomiala, iar EXP cea a problemelor cu complexitate
exponentiala; intre aceste doua clase exista o sumedenie de
clase intermediare, de exemplu cea a problemelor cvasi-polinomiale, care sunt
mai mari decat cele polinomiale, dar mai mici decat cele exponentiale (de
exemplu functia nlog n). Chiar un rezultat care ar separa NP de EXP ar fi grozav, pentru ca ne-ar da solutii pentru
problemele din NP mai bune decat
cunoastem la ora actuala.
Teoreticienii aveau practic doua scule fundamentale in
repertoriu pentru a rationa despre complexitate: diagonalizarea si
simularea, ambele prezentate pe scurt in prima parte a acestui articol, in
numarul anterior al revistei.
Simularea se foloseste de faptul ca o masina
Turing adesea se poate comporta ca o alta masina Turing, "simulindu-i"
executia. Aceasta tehnica se numeste in viata de zi cu
zi "interpretare", si este exact ceea ce se intampla cu limbajele
interpretate: BASIC, Lisp etc.: interpretorul de BASIC simuleaza
executia programelor scrise in BASIC.
Diagonalizarea este o tehnica foarte ingenioasa pentru a
arata ca un obiect nu este intr-o multime, pentru ca este
diferit de fiecare obiect din multime printr-o anumita
trasatura.
Teoreticienii au incercat sa demonstreze ca P 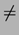 NP aratand ca masinile
din NP sunt diferite de toate masinile
din P. Dar aceste incercari
au fost brusc curmate de un rezultat socant.
NP aratand ca masinile
din NP sunt diferite de toate masinile
din P. Dar aceste incercari
au fost brusc curmate de un rezultat socant.
Clase de complexitate importante
Deocamdata punem deoparte notiunea de reducere, si
discutam clasele de complexitate cele mai importante studiate. Pentru
fiecare din aceste clase se cunosc probleme complete. Vom prezenta clasele in
ordinea crescatoare a complexitatii lor; cel mai adesea
insa relatia reala intre clase consecutive este
necunoscuta.
Spatiu
constant
Prima clasa interesanta de complexitate este cea a
masinilor care folosesc o cantitate fixa de spatiu pentru
a-si face calculele, care cantitate este independenta de marimea
datelor de intrare. Chiar cand datele de intrare tind la infinit, masina
foloseste la fel de putin spatiu.
Un fapt interesant despre aceasta clasa este ca, de
fapt, daca dai unei masini spatiu constant, nu are ce face cu
el: exista o alta masina care face acelasi lucru
fara nici un fel de spatiu suplimentar. Exista un nume special
pentru masinile Turing care nu folosesc nici un fel de spatiu pe banda
(in afara de a citi sirul de la intrare): ele se numesc automate
finite.
Toate limbajele care se pot decide in spatiu constant se
numesc limbaje regulate. Aceste limbaje sunt extrem de importante in
practica; exista o seama intreaga de medii de programare
care manipuleaza limbaje regulate. Programe si interpretoare faimoase
care manipuleaza limbaje regulate sunt Perl, Lex, grep, awk, sed etc. Perl
este de pilda limbajul preferat pentru a scrie extensii pentru serverele
de web de pe Internet.
Limbajele regulate sunt atat de utile pentru ca se
demonstreaza ca ele pot fi acceptate in timp linear: cu alte cuvinte
pentru orice limbaj regulat exista o masina Turing care decide
un cuvant de lungime n in timp O(n). Acest timp este practic cel mai mic timp
posibil, pentru ca in mai putin de O(n) nu putem nici macar citi
toate literele de la intrare!
Un exemplu de limbaj regulat ne-trivial: adunarea. Daca
primim trei numere, a, b, c, scrise intretesut pe banda (adica o
cifra de la a, una de la b, una de la c, atunci putem verifica folosind un
automat finit daca c = a+b.
Spatiu logaritmic
O clasa foarte interesanta de complexitate este cea a
limbajelor care pot fi acceptate folosind spatiu logaritmic in lungimea cuvantului
de intrare. Pentru orice cuvant de lungime n masina foloseste nu mai
mult de O(log n) celule de memorie pentru a procesa cuvantul.
Clasa aceasta se noteaza cu L, de la Logaritm. Se arata ca aceasta clasa
este strict mai cuprinzatoare decat cea a limbajelor regulate: exista
limbaje ne-regulate in L.
De ce folosim tocmai logaritmul? In spatiu logaritmic
masina poate manipula un numar finit de contoare a
caror valoare este cuprinsa intre 1 si n (fiecare contor are log
n cifre). Putem spune deci ca clasa L este cea a masinilor care au nevoie doar sa
tina minte cateva pozitii din sirul de intrare, si
nimic mai mult.
Ce putem face in spatiu logaritmic? O multime de
lucruri! De pilda putem inmulti doua numere: folosim contoare
pentru a parcurge numerele de inmultit, si pentru a face adunarea de
la dreapta la stanga.
O alta problema foarte importanta pe care o putem
rezolva doar in spatiu logaritmic este de a calcula valoarea unei formule booleene,
atunci cand cunoastem valorile tuturor variabilelor care o compun.
Timp polinomial
Cea mai folosita clasa de complexitate este cea a
timpului polinomial, notata cu P.
Putem defini foarte precis P
matematic folosind urmatoarea notatie TIME(f(n))= clasa problemelor
care se pot decide in timp f(n). Atunci 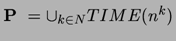 .
.
Se arata imediat ca orice se poate calcula in
spatiu logaritmic, nu are niciodata nevoie de mai mult decat timp
polinomial, sau altfel spus, 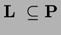 .
.
Practic toti algoritmii eficace invatati in
scoala sunt din clasa P;
teoreticienii considera ca daca o problema nu este in P, atunci nu poate fi rezolvata
practic, pentru ca resursele cerute sunt prea multe. De exemplu, programarea
lineara, algoritmul Gauss-Seidel de inversare a unei matrici, sau
algoritmul care calculeaza iesirea unui circuit combinational cand
intrarea este data, sunt toti algoritmi de timp polinomial.
De fapt ultima problema este chiar P-completa, vis-a-vis de reduceri in spatiu logaritmic.
Deci orice alta problema din P
se poate reduce la problema evaluarii unui circuit boolean! Observati
ca evaluarea unui circuit boolean este mai dificila decat a unei
formule booleene, desi orice formula boolean poate fi scrisa ca
un circuit.
Relatia exacta dintre L si P nu este
cunoscuta; nu se stie daca L este strict inclusa in P sau cele doua clase sunt de fapt egale. Daca cineva ar
gasi o metoda de a rezolva problema valorii unui circuit boolean
folosind un algoritm din L,
atunci am demonstra automat ca L
= P, datorita
completitudinii problemei.
Aceasta intrebare este foarte importanta pentru
practica, pentru ca algoritmii din L pot fi asimilati cu algoritmii care se pot executa foarte
eficient pe o masina masiv paralela. Chestiunea L = P se poate deci interpreta ca intrebarea: "poate orice algoritm
din P fi executat foarte
eficient in paralel?".
Spatiu polinomial
In general este usor de vazut ca daca o
problema are nevoie de timp t atunci nu consuma mai mult de
spatiu t, pentru ca in fiecare unitate de timp poate consuma cel mult
o unitate noua de spatiu. Daca notam cu PSPACE clasa problemelor care
consuma spatiu polinomial in marimea datelor de intrare, atunci
avem deci imediat P 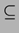 PSPACE.
PSPACE.
Ce putem rezolva avand la dispozitie spatiu polinomial?
Ei bine, putem rezolva toate jocurile cu informatie perfecta. Mai
mult decat atat, aceste probleme sunt PSPACE-complete
vis-a-vis de reduceri in timp polinomial. Ce sunt jocurile cu informatie
perfecta? Sunt toate jocurile gen Go sau dame pe table de marime n x
n (aceasta este marimea datelor de intrare). As spune sah, dar
este destul de greu de generalizat sah-ul pentru table arbitrar de mari.
Asa cum stim din teoria jocurilor (sau daca nu
stim, va spun eu), orice joc de acest gen are o strategie
perfecta pentru fiecare jucator, care obtine cel mai bun
rezultat, independent de miscarile celuilalt. Problema de a afla
daca primul la mutare poate castiga mereu este cea a jocurilor cu
informatie perfecta.
In mod surprinzator (sau poate v-ati obisnuit cu
aceste intrebari nerezolvate, si vi se pare naturala
ignoranta noastra in acest domeniu), nimeni nu stie daca P= PSPACE. Ceea ce stim cu siguranta este ca L 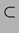 PSPACE este o incluziune stricta.
PSPACE este o incluziune stricta.
Interesant, anumite probleme practice foarte utile sunt de
asemenea PSPACE-complete; de
exemplu problemele de planificare care apar in inteligenta
artificiala, cum ar fi programarea traseului unui robot. O alta
problema importanta care este completa pentru PSPACE este problema pe care o intalnesc
cei care scriu compilatoare atunci cand analizeaza un program cu pointeri
pentru un limbaj ca C, care permite crearea de pointeri catre
functii: determinarea la compilare a informatiei "points-to", care
spune spre care obiecte un pointer poate arata, este si ea
completa pentru PSPACE.
Timp
exponential
Desi nu am aratat cum, acelasi gen de
demonstratie care arata ca L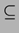 P poate fi folosit pentru a
arata ca PSPACE
P poate fi folosit pentru a
arata ca PSPACE 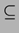 EXP. EXP este definita ca fiind clasa tuturor problemelor care se
rezolva in timp exponential:
EXP. EXP este definita ca fiind clasa tuturor problemelor care se
rezolva in timp exponential: 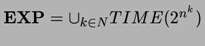 .
.
Nu avem habar daca incluziunea PSPACE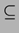 EXP este stricta sau nu.
EXP este stricta sau nu.
Spatiu exponential
Daca putem folosi timp exponential, putem folosi si
spatiu exponential. Aceasta clasa monstruoasa este
putin intalnita in practica, desi exista probleme
practice care pot fi plasate aici.
Dincolo de spatiu exponential
Exista si clase de complexitate mai mari decat acestea.
Vom prezenta o astfel de clasa in ultima parte a acestui text, intr-un
numar ulterior, cand discutam despre complexitatea de decizie a
feluritelor teorii logice.
Complexitatea nedeterminista;
masini alternante
Modelul de masina cu care am lucrat pana acum este
destul de realist, in sensul ca pare imediat construibil in practica.
Singura ciudatenie abstracta au fost oracolele.
Dar asa cum modelul ezoteric al oracolelor, desi
ne-implementabil, a fost de o enorma importanta
metodologica, permitandu-ne sa tragem niste concluzii
foarte importante, teoreticienii au mai elaborat doua variatiuni la
modelul masinilor Turing, care se dovedesc extrem de importante in
practica.
Modelele pe care le voi introduce acum pot fi simulate cu
masini Turing obisnuite, cu o pierdere oarecare de eficacitate. Dar
prezenta acestor masini ne permite sa facem niste diviziuni
mai fine in interiorul feluritelor clase de complexitate, si sa punem
niste intrebari foarte importante.
Masini nedeterministe
Va reamintiti ca definitia masinii Turing
spunea exact ce trebuie sa faca automatul in fiecare stare, in
functie de simbolul de pe banda. Ei bine, acum vom permite o oarecare
ambiguitate: masina noastra va avea posibilitatea sa faca
nu una, ci mai multe miscari la un moment dat.
Trebuie sa redefinim conceptul de acceptare: inainte
masina accepta daca secventa ei de stari parcurse se
termina cu o stare anumita, numita "acceptare". Dar acum, cand
masina poate urma mai multe trasee, care este criteriul de acceptare? Vom
spune ca masina accepta atunci exista cel putin o
carare care duce la o acceptare.
Figura 6 arata cum stau lucrurile cu astfel de
masini.
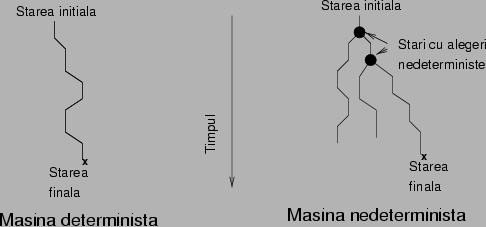
Figura 6: O masina determinista, de
indata ce are un sir pe banda de intrare, are o traiectorie
fixata in spatiul starilor: putem spune oricand in ce stare
masina se va afla. Prin contrast, masinile nedeterministe se pot afla
in stari cu mai multi succesori, in care pot alege traiectoria. O
masina determinista accepta daca cel putin o
traiectorie a ei accepta.
Intuitiv putem sa ne imaginam astfel de masini in
doua feluri; alegeti-l pe cel preferat:
Putem sa ne imaginam ca masina atinge astfel
de puncte de decizie cu posibilitati multiple de executie,
si atunci pur si simplu ghiceste pe care carare s-o ia.
Daca exista o secventa de ghiciri bune, masina va
accepta. Aceasta perspectiva este adesea folosita, iar
masinile de acest gen se numesc "nedeterministe", pentru ca
comportamentul lor nu mai poate fi descris dinainte precis.
Un alt model de reprezentare foloseste fire (threads) de
executie multiple: ne putem imagina ca masina noastra poate
executa in paralel un numar nelimitat de fire de executie. Atunci cand
masina atinge un punct de alegere nedeterminista, creeaza cate
un fir de executie separat pentru a explora fiecare posibilitate. Aceste
fire se vor executa apoi perfect in paralel, iar primul care va gasi
solutia va termina intregul proces de calcul.
Masinile nedeterministe le generalizeaza pe cele
deterministe; par de asemenea mai puternice: e clar ca orice problema
care se poate executa in timp determinist T se poate executa si in timp
nedeterminist T, pentru ca orice masina determinista este un caz
particular de masina nedeterminista.
Apar astfel clasele de complexitate prefixate cu litera N: NL, NP, NPSPACE, NEXP. De asemenea, o clasa nedeterminista este mai
slaba decat clasa determinista superioara: avem ierarhia: 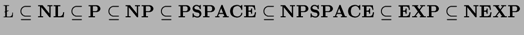 . Despre majoritatea incluziunilor din acest
lant nu stim daca sunt stricte.
. Despre majoritatea incluziunilor din acest
lant nu stim daca sunt stricte.
Un singur rezultat pozitiv lumineaza aceste incertitudini: in
mod surprinzator in 1970 Savitch a demonstrat ca PSPACE = NPSPACE, deci nedeterminismul nu ajuta cu nimic puterea
computationala pentru acest gen de probleme.
In plus mai stim adesea ca anumite incluziuni intre
clase distante sunt stricte: de exemplu avem teoreme de genul "fie L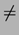 P, fie P
P, fie P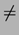 PSPACE", sau, mai simplu spus,
PSPACE", sau, mai simplu spus, 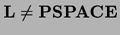 .
.
Asa cum am mai mentionat, clasa asupra careia s-au
aplecat cei mai multi cercetatori este NP. Articolele mele anterioare aratau ca problema
satisfiabilitatii booleene ("are un circuit boolean intrari
pentru care iesire este 1") este completa pentru NP vis-a-vis de reduceri polinomiale.
O sa mentionez in final o problema completa
pentru NEXP: jocul de poker
generalizat in trei adversari (jocuri in mai multe persoane, cu aleatorism
si informatie ascunsa).
Clase complementare
O intrebare naturala este: daca putem generaliza
masina Turing sa aiba astfel de stari in care poate face o
alegere, nu putem crea si niste stari speciale in care orice
alegere sa trebuiasca sa duca la o stare acceptoare? In
modelul paralel, cu fire de executie, cerem ca toate firele
lansate in paralel sa termine cu succes, si nu unul singur dintre
ele.
Vom distinge deci doua tipuri de stari: starile existentiale:
cel putin o carare care iese din ele trebuie sa duca la o
acceptare (acestea sunt starile din masinile nedeterministe,
introduse mai sus), si starile universale: toate
cararile plecand din acea stare trebuie sa duca la o
acceptare.
Intr-adevar, aceste masini recunosc alte clase de
limbaje. O masina care are doar stari universale recunoaste
anumite clase de limbaje interesante. Se poate arata ca aceste
limbaje sunt complementele limbajelor acceptate de masinile
nedeterministe, de aceea numele lor se prefixeaza cu "Co". De exemplu,
avem clasa limbajelor CoL, care
pot fi acceptate de o masina cu stari universale in spatiu
logaritmic. Avem CoNP, limbajele
care pot fi acceptate de masinile polinomiale cu stari universale.
Din nou, masinile perfect deterministe sunt un caz particular
de masini cu stari universale, in care in fiecare stare avem o
singura decizie posibila. De aici rezulta imediat o serie de
incluziuni: 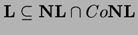 ,
, 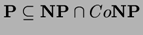 etc.
etc.
Ca sa fim mai concreti, sa vedem o problema
care este in CoNP. Problema este
foarte interesanta: daca am doua harti, sunt ele ne-izomorfe?
Adica, oricum as asocia tarile dintr-una cu
tarile din cealalta, nu voi obtine niciodata
aceeasi relatie de vecinatate (daca sunteti familiari
cu terminologia grafurilor, aceasta este de fapt problema non-izomorfismului
grafurilor).
Aceasta problema este in CoNP, pentru ca vreau sa verific ca orice
permutare a unei harti este diferita de cealalta. Putem
deci construi o masina cu o stare universala, din care se
exploreaza in paralel toate permutarile posibile.
Vedeti, problema cealalta, a izomorfismului grafurilor
este in NP: "sunt doua
grafuri izomorfe?" se poate rezolva in timp nedeterminist polinomial.
Complementul acestei probleme este insa in CoNP. E interesant de observat ca adesea o problema nu
este la fel de grea ca problema complementara. De pilda, e usor
sa demonstrezi ca nu a plouat peste noapte: strazile sunt
uscate. Dar daca strazile sunt ude, nu poti sa stii
daca nu cumva au spalat strada. Un lucru si complementul lui nu
sunt la fel de usor de demonstrat.
De fapt aici nu am exprimat decat o credinta:
relatia dintre clasele de complexitate si complementele lor este cel
mai adesea necunoscuta; singurul rezultat concret este dat teorema Immerman-Szelepcsényi,
din 1988, care arata ca NL =
CoNL.
Intrebarea NP = CoNP este o intrebare cu consecinte
foarte importante pentru practica; daca aceste clase sunt egale (ceea
ce lumea crede foarte putin probabil), atunci exista
demonstratii scurte pentru non-izomorfismul grafurilor: poti scrie o
dovada sumara ca doua grafuri nu sunt identice.





