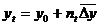Seriile dinamice in econometrie

Seriile dinamice in econometrie

Un sir de valori pe care le inregistreaza la momente sau intervale de timp succesive o anumita caracteristica statistica la o unitate sau o colectivitate statistica reprezinta o serie dinamica (sau cronologica).  

Prin studierea seriilor dinamice se studiaza variatia in timp a unui fenomen evidentiindu-se cresterile sau descresterile de nivel, modificarile de structura. In functie de scopul urmarit, exista mai multe metode de observare si analiza a acestor serii [51,pag.128]:

Pentru a stabili nivelul si modificarea de nivel, in timp, a unui fenomen se folosesc indicatorii de nivel, exprimati in marimi absolute, relative sau medii;

Pentru a determina variatia de la o perioada la alta si influenta factorilor se foloseste metoda indicilor dinamicii fenomenelor;

Pentru estimarea tendintai (trendului), a oscilatiilor sezoniere si a variatiilor aleatoare se foloseste metoda de analiza a componentelor;

Pentru extrapolarea trendului se folosesc metode de prognoza statistica.

Din punct de vedere econometric, aceste serii ajuta la dezvaluirea unor regularitati intr-un proces evolutiv, ceea ce inseamna un pas inainte spre specificarea precisa a unor variabile care actioneaza in timp, reprezentand totodata "masura artificiala" a unor variabile necuantificabile dar care sunt elemente ale mecanismului economic studiat.

In cadrul econometriei se urmaresc, in determinarea trendului trei tendinte:

Trendul direct, ce se refera la anumite fenomene ce nu pot fi nemijlocit specificate;

Trendul ca factor auxiliar in functii in care nu toti factorii care actioneaza asupra unui proces pot fi explicitati;

Trendul care face separare analitica a acelor factori care sunt specificati dar nu sunt in acelasi timp cuantificabili.

Majoritatea seriilor dinamice intalnite in economie au o tendinta de lunga durata, peste care, acolo unde este cazul se suprapun componente ce contin modificari:

Ciclice reprezentate de oscilatii in jurul tendintei generale, oscilatii care au o anumita periodicitate in manifestare;

Sezoniere, generate de actiunea unor factori sezonieri, care apar de obicei pe parcursul unui an. Aceste oscilatii se produc sub influenta unor factori naturali - climatici (productia agricola) sau cu caracter social (concedii, sarbatori, traditii), lungimea lor fiind de regula constanta;

Accidentale, care apar datorita unor factori intamplatori, cu actiune imprevizibila. Se manifesta sub forma unor abateri de la ceea ce este sistematic in evolutia fenomenului analizat. Erorile de observare a datelor se inscriu tot in aceasta categorie.

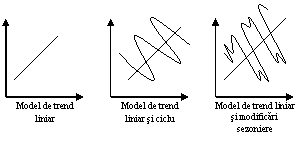
- Fig.3.6 -

In functie de aceste componente, prezentam schematic cateva modele de evolutii in dinamica (fig.3.6).

Metoda de determinare si analiza a trendului

Deoarece sistemul de indicatori ai unei serii dinamice nu este suficient pentru a releva schimbarile care au loc in fiecare an, cele datorate unei miscari de durata (chiar cu tendinta seculara), cele cu oscilatii nesistematice sau cele ciclice (care pot fi periodice sau neperiodice) este necesar sa apelam la modelarea acestora. In general agregarea celor patru componente ale unei serii dinamice: trendul (T), componenta ciclica (C), componenta sezoniera (S) si componenta aleatoare (E) se face prin combinarea acestora fie ca model aditiv (fig.3.7) de combinare a componentelor unei serii dinamice T = C + S + E,

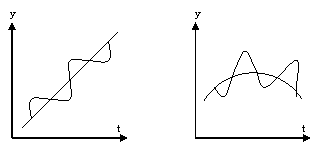
Model aditiv de combinare a componentelor unei serii dinamice

- Fig.3.7 -

fie ca model multiplicativ T = C · S · E (fig.3.8) de combinare a componentelor unei serii dinamice

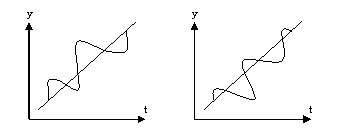
Model multiplicativ de combinare a componentelor unei serii dinamice

- Fig.3.8 -

In practica, insa, aceasta analiza nu urmeaza intotdeauna un anumit model si atunci trebuie ales un model care sa aproximeze cel mai bine evolutia reala a fenomenului studiat. Cunoasterea tendintei, a legii de evolutie a procesului economic studiat nu este insa posibila decat prin masurarea actiunii fiecarei categorii de factori implicati.

In sens larg, a determina trendul unei serii dinamice sau a ajusta o astfel de serie inseamna a inlocui termenii sai y_i, 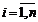cu termenii y_i^* ai unei serii teoretice, y_i^* fiind obtinuti prin metode de cuantificare si eliminare a abaterilor provocate de factori cu caracter periodic si aleator.

Analiza acestor serii de date statistice pentru elaborarea studiilor previzionale porneste de la inceput de la ipotezele formulate de stiintele economice, pentru ca din datele respective nu rezulta de cele mai multe ori daca intre fenomene exista sau nu o legatura cauzala sau de asociere. Daca dependenta dintre date a fost admisa, trebuie stabilita forma acestei dependente, adica descrierea legaturii dintre fiecare valoare a variabilei dependente si fiecare valoare a variabilei sau variabilelor interdependente ale seriilor de date statistice. Conceptul de ajustare porneste de la ipoteza ca legatura poate fi descrisa dar nu neaparat si explicata [A]. Functia econometrica ce formalizeaza matematic legatura dintre doua variabile genereaza, pentru variabila dependenta, o noua serie de date y_i^*. Descrierea cu suficienta precizie a formei legaturii dintre variabile presupune cunoasterea unor serii de date statistice suficient de lungi, ceea ce de multe ori este greu de asigurat. Subliniem ca in calcule nu se urmareste stabilirea unor corelatii exacte ci a unora convenabile, cu abateri minime fata de datele reale, iar rezultatele obtinute cu ajutorul functiilor econometrice trebuie neaparat asociate si cu alte metode de analiza sau cercetare prospectiva, atat pentru compararea rezultatelor cat si pentru sporirea gradului de siguranta.

Metoda folosita frecvent pentru elaborarea studiilor previzionale prin "prelungirea tendintelor trecute ale variabilelor", care se bazeaza pe cunoasterea relatiilor cauzale este metoda extrapolarii. "Extrapolarea transporta in mod simplist trecutul spre viitor" [15,pag234]. Exista doua modalitati de aplicare a acestei metode: extrapolarea mecanica si extrapolarea euristica si mai multe procedee de extrapolare: extrapolarea analitica; extrapolarea prin curbe infasuratoare; extrapolarea fenomenologica.

Extrapolarea mecanica presupune ca relatiile formate intre variabile nu se modifica in viitor, admitand astfel, prin continuitate, prelungirea tendintelor manifestate in trecut.

In cadrul extrapolarii euristice, pornindu-se de la analiza perioadei precedente, se introduc anumite corectii in curba de evolutie viitoare a fenomenului in functie de modificarea previzibila a desfasurarii fenomenului sau de anumite optiuni ale factorilor de decizie.

Extrapolarea analitica pleaca de la o serie de valori ale seriei dinamice, valori pe care le prelucreaza putand astfel sa estimeze comportarea ulterioara a fenomenului descris de seria respectiva. Aceasta extrapolare se realizeaza cu ajutorul sporului mediu absolut, al ritmului mediu anual si al functiilor de corelatie. Formula folosita in aceasta situatie este:

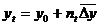
unde y_t este valoarea variabilei de previziune in anul final al orizontului, y₀ valoarea variabilei in anul de baza, 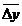sporul mediu absolut al variabilei de previziune in perioada statistica, iar n_t este numarul anilor din perioada de previziune.

In cazul unei extrapolari euristice, sporul mediu absolut se corecteaza prin inmultire cu un coeficient k (subunitar sau supraunitar, dupa cum se apreciaza modificarea tendintei evolutiei):

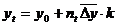
Extrapolarea cu ajutorul ritmului mediu anual se aplica in special cand este vorba despre fenomene ce evolueaza sub forma de progresie geometrica:

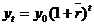
in care 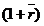este ritmul mediu anual de crestere a variabilei, iar t numarul de ani ai perioadei de previziune.

La fel ca mai sus, in cadrul extrapolarii euristice se utilizeaza coeficientul 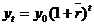k:

k

Alegerea si estimarea unei curbe. Cea mai dificila problema de determinare a trendului este alegerea tipului de functii si estimarea parametrilor. Functia aleasa trebuie sa descrie in modul cel mai adecvat tendinta de evolutie din perioada precedenta, tendinta care se presupune ca se va afirma si in viitor. De aceea sunt necesare urmatoarele succesiuni [15,pag.236]:

Definirea obiectului previziunii care conditioneaza, fixarea orizontului de previziune si stabilirea gradului de siguranta al acesteia;

Alegerea variabilelor independente;

Determinarea perioadei pentru analiza retrospectiva;

Alegerea functiei de extrapolare care descrie cel mai bine evolutia trecuta a variabilei dependente;

Estimarea parametrilor functiei de extrapolare sau parametrizarea acesteia;

Aprecierea calitatii functiilor de extrapolare cu ajutorul estimatorilor statistici;

Efectuarea calculului de previziune (particularitati in raport cu modelul econometric al functiei de extrapolare);

Analiza economica a rezultatelor obtinute, pentru a selecta cea mai buna varianta din mai multe posibile.

Reprezentarea grafica este metoda cea mai simpla si poate da rezultate satisfacatoare in cazul functiilor de trend si de corelatie simpla.

O metoda cu mai mare precizie este metoda Hanstein sau analitica. Aplicarea acestei metode necesita urmatoarele operatii:

Calculul fuctiilor asociate unei functii de extrapolare;

Reprezentarea grafica a functiilor asociate;

Analiza comparativa a reprezentarilor respective cu graficele corespunzatoare asociatelor unor functii de extrapolare.

Fiecare functie de extrapolare are trei functii asociate, cu ajutorul carora se pot aprecia directiile de crestere, natura procesului, simetria etc [A].

Derivata absoluta:

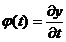ceea ce in cazul diferentelor finite devine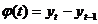

Derivata relativa:

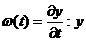ceea ce pentru diferente finite inseamna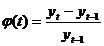

Functia de elasticitate:

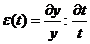sau, pentru diferente finite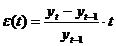

Revenind asupra celor trei tendinte urmarite in econometrie in determinarea trendului subliniem ca functiile de extrapolare pot fi functii de corelatie, cand variabila sau variabilele independente sunt marimi economice sau tehnice, ca de exemplu y = f(x) sau y = f(x_i) si, functii de tendinta, adica y = f(t). Cele mai cunoscute modele matematice ale functiilor de extrapolare sunt functiile liniare, parabolice, exponentiale, hiperbolice, logaritmice, logistice etc. Pentru estimarea parametrilor acestor functii se foloseste metoda celor mai mici patrate pe care am prezentat-o in subcapitolul 2.2.

Extrapolarea cu ajutorul curbei infasuratoare consta in reprezentarea grafica a mai multor curbe de evolutie a unor activitati si extrapolarea tendintelor pe o infasurare, chiar daca nu se cunoaste cu siguranta solutia concreta ce va apare in viitor.

In literatura economica notiunea de curba infasuratoare este definita de profesorul M.Botez in cursul sau de prognoza astfel [15,pag151]:

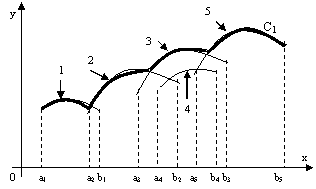
Curba infasuratoare de speta I

- Fig.3.9 -

Daca este o familie finita de functii pozitive f_α(x) ≥ 0 definite pe intervalele I_α = (a_α,b_α) si curbele care reprezinta grafic aceste functii se numeste infasuratoare de gradul I a acestei familii functia care este definita pe 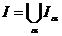, care asociaza oricarui 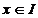numarul 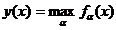. Notam C₁ curba infasuratoare a acestei functii (fig.3.9) care este, de fapt, o reuniune de portiuni ale unei curbe g_α.

Considerand aceeasi familie de curbe numim infasuratoare de speta a II-a a acestei familii, curba C₂, tangenta tuturor curbelor acestei familii (fig.3.10).

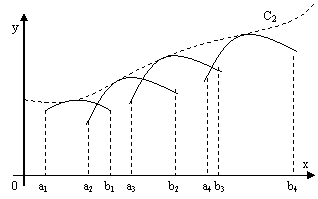
Curba infasuratoare de speta a II-a

- Fig.3.10 -

O analiza globala a fenomenului in urma caruia sa se deduca legile ce guverneaza variabila respectivului fenomen se face cu ajutorul extrapolarii fenomenologice. Aceasta metoda urmareste identificarea unor legi in evolutia fenomenului studiat si incearca sa descrie variatia pe baza acestora, concentrandu-se pe analiza factorilor ce modifica tendintele manifestate in perioada trecuta. De exemplu, o functie de forma

y = a ± b^kt

este pusa in evidenta de studierea variatiei randamentelor agregatelor si a consumului specific de combustibil in analizarea evolutiei productiei de energie electrica.