Proiectare Logica - Teoremele lui De MORGAN

Proiectare Logica - Teoremele lui De MORGAN

T1)

Suma logica a unor termeni este egala cu produsul logic al termenilor negati:

negata(∑ Pi) = ∏ negata(Pi)

T2)

negata(∏ Sj) = ∑negata(Sj)

T1)-caz elementar

(x+y)'=x' * y'

Demonstratie:

Demonstratie generala:

neg( ∑(1->n) Pi )= neg( ∑(1->n-1)Pi + Pn )= neg(∑(i->n-1)) * neg(Pn). Demonstratie generala se face prin inductie

T2)-caz elementar

(x*y)'= x' + y'

Tot prin inductie demonstratia, analog T1.

T1) Aplicatie

f=x * y' + a' * b * c; (1)

(((f)')'=f;

neg(neg(f))=neg( ((x*y')' * (a' * b*c)' )' (2)

nand1 nand2

( ----- nand3 ------ )

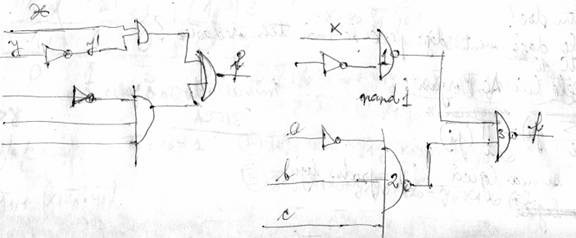
Reprezentarea functieei f

Concluzia: o forma de tip disjunctiv in ordinea not, and, or (in ordinea asta) se transforma prin dubla negatia (efect al T1) in formule de tip nand.

neg ( neg(∑Pi) ) = neg (∏(neg(Pi))). Forma disjunctiva se converteste direct in porti de tip nand.

neg (neg (∏ Sj ))= neg (∑ neg (Sj))

T2) aplicatie

g= (x+y')*(a'+b+c) ->forma conjunctiva - produs de sume (1)

Ce relatie exista intre f si g? f diferit de g

((g)')' = (( x+y')' + (a'+b+c)' )'

Nor1 nor2

Nor3

Spatiul logic n-dimensional este multimea tuturor punctelor (combinatiilor posibile) a n variabile logice independente intre ele. Caracteristicele de baza, variabilele fiind independente: spatiu intreg, discret, are 2^n combinatii. Spatiul logic fiind discret si finit contine 2^n puncte sau combinatii.

Reprezentari lineare ale spatiului logic.

Exemple cu S4 - 4 dimensiuni.

Coloana lui x0 comuta la fiecare linie. Coloana lui x1 comuta la 2 linii. De sus in jos bitii isi schimba valoarea(comuta) atunci cand bitul din dreapta se schimba din 1 in 0.

TCP - termen canonic de tip rodus

TCS - termen canonic de tip suma

Negata lui TCS e TCP si invers (T1 + T2).

neg(TCP)=TCS; neg(TCS)=TCP; Termenii canonici de tip produs sau suma sunt duali. Suma logica si produsul logic sunt operatori de tip dual in sensul ca pentru aceasi combinatie de intrare suma respectiv produsul sunt complementare.

Concluzii generale: primele 4 coloane sunt reprezentarea vectorului in codificare direct crescatoare (Direct Binary Coding).

A 2-a metoda de reprezentare (tot lineara). Codificare GRAY - cod ciclic reflectat

Distanta lineara intre 2 puncte din spatiu - distanga HAMMING dH = nr de biti prin care difera cele doua coduri. Puncte adiacente-dH=1. Punctele identice sunt considerate ca un caz extrem de adiacenta.

Fiecare combinatie in GRAY e adiacenta cu vecinii. Si primul cu ultimul. De aia i se zice ciclic ca sa nu mai zic ca de oriunde incepem numaratoarea tot ciclic e.

Se vad si niste reflectii pe aici, cu trecere de la x1 la x2 si apoi la fiecare adaugare de coloana. Alea rosii sunt axele de simetrie si ingrosate thanks to Bug. Punctele simetrice in functie de axele de simetrie sunt adiacente

Maparea bidimensionala a spatiului logic n-dimensional.

Sn=

k,n-k

Combinatiile celor k biti vor codifica intr-un tablou bidimensional coloanele, iar ceilalti randurile.

EXEMPLU

5 biti

3 pt randuri, 2 pt coloane, random

k=2, n=5

2^2 coloane

2^3 linii

x4 x3 x2

x1,x0

Fiecare linie si fiecare coloana a celor 2 respectiv 3 biti care definesc spatiul 5-dimensional. Am facut in cod Gray, dar se putea face si in cod direct la fel de bine.

Fiind Gray: proprietati:

simetria de reflectie din tabelul de la pag3

orice axa orizontala este axa de simetrie/de adiacenta pt punctele vecine. Daca axa imparte zona in doua parti egale (cum ar fi aia ingrosata), atunci randurile egal departate sunt adiacente.

Diagrama asta se numeste KARNAUGH (pr: carnaf) - K-map.

Subspatiii ale lui Sn:

Prin Sj inclus in Sn se intelege o submultime de 2^(n-j) puncte cu proprietatea ca j biti sunt constanti, restul n-j biti parcurg tot ciclul de variatie. Pentru j=0 Sj=Sn, iar pentru j=n totul e constant-puncte individuale.

Orice subspatiu poate fi definit prin specificarea tuturor codurilor care variaza pe bitii variabili sau prin reciprocitate a bitilor care raman constanti.

f=x* y' + a' * b * c

Linia 1: "-" este valoarea indiferenta - don't care. ori 0 ori 1. deci bitii a,b,c parcurg tot ciclul de variatie. Deci x * y' in S5 este un subspatiu de tip S2.

Daca un termen este complet (are 5 valori fixate), atunci el este reprezentantul unui singur punct- termen canonic.

Formele canonice ale functiilor logice

-forme canonice de 2 tipuri: - suma de produse logice(disjunctiva) / -

f=x*y'*( (a)'*(b)'*(c)'+a'*(b)'*c + a'*b*c'+ . abc) +

a'*b*c*( x*y + x'*y+xy'+x'y' ) - dezvoltare

dezvoltare=trecere de la forma elementare la forma canonica prin completarea variabilelor care sunt implicite(nementionate, don't care). Operatia inversa dezvoltarii se numeste simplificare. Simplificarea ultima posibila se numeste minimizare a functiei.

Hai sa facem o simplificare:

H=x4' *x3'*x2'*x1*x0+x4'*x3*x2'*x1*x0+x4*x3'*x2'*x1*x0+x4*x3*x2'x1x0

H=x4'*x2'*x1*x0 + x4*x2'*x1*x0

H=x2'*x1*x0

Concluzie: data doi termeni canonici au cod binar adiacent, expresiile analitice de tip produs difera printr-un singur bit.

Pentru numere pe 5 biti sa se faca o functie care sa dea 1 daca numerele se impart la 3 sau la 5.

UTILIZAREA DIAGRAMELOR K pentru simplificarea functiilor logice

X=

Y=

X>Y=1 daca (x1,x0) > (y1,y0)

Sa se scrie forma canonica a acestei functii (alfa=x>y).

(a+b)+(c+d): y1'y0'x1x0+y1'y0'x1x0'+y1'y0x1x0+y1'y0x1x0'=

=y1'y0'x1+y1'y0x1=y1'x1;

e: y1'y0'x1'x0+y1'y0'x1x0=y1'y0'x0;

f: y1'y0'x1x0+y1y0'x1x0=y0'x1x0

Deci functia f =y1'x1+y1'y0'x0+y0'x1x0;

ceea ce se putea vedea din faptul ca y1-0 si x1=0 in patratelele alea.

asa se grupeaza scriindu-se la final in modul minimal.

Principiul de simplificare in K-Map este urmatorul:

-se determina subspatiile de acoperire cu valorile logice 1 ale functiei date (un subspatiu este caracterizare de 2^k puncte care sunt despartite de axe de simetrie). Operatiunea se repeta pana cand am acoperit toate valorile unu.

Titlurile lectiei viitoare:

-functii incomplet specificate

-proiectarea generala a unui comparator de marime

-procedee de insumare, sumator complet (sumator de unu si doi biti).