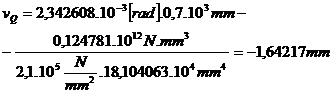Metoda grafo-analitica de integrare a
ecuatiei diferentiale de ordinul al II-lea a fibrei medii deformate
Fie bara din figura 16 , incarcata cu o
sarcina distribuita oarecare, ecuatia fibrei medii deformate
este :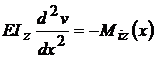 ; prin integrare se
va obtine,
; prin integrare se
va obtine, 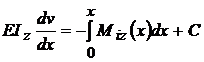 ;
;
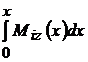 = Aox ,
reprezinta aria diagramei de
= Aox ,
reprezinta aria diagramei de
momente incovoietoare pe portiunea o-x care se noteaza cu Aox . Implica
relatia, 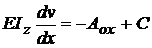 ; constanta
C se calculeaza
; constanta
C se calculeaza
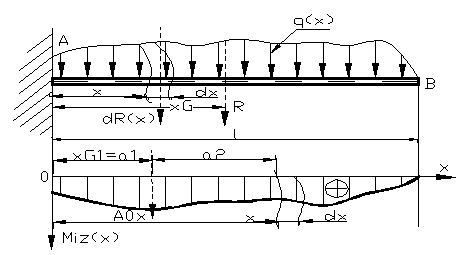
Figura
16
din conditia
initiala a lui Cauchy,
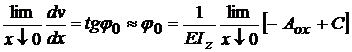 ;
; 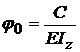 ;
;
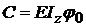 ; A00 = 0 ;
; A00 = 0 ;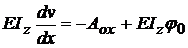 ; se integreza inca o data si vom
obtine:
; se integreza inca o data si vom
obtine: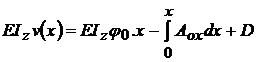 .
.
Acum se integreaza prin
parti 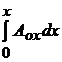 ; f ( x ) = Aox ;
; f ( x ) = Aox ; 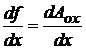 ; dg = dx ;
; dg = dx ; 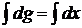 ; g ( x ) = x ; formula de integrare prin parti
este:
; g ( x ) = x ; formula de integrare prin parti
este: 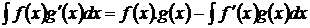 ;
;
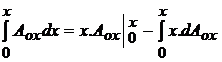 ; cum din figura
16 , reiese ca
; cum din figura
16 , reiese ca
x = a1 + a2 , iar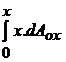 reprezinta momentul static al suprafetei
reprezinta momentul static al suprafetei
diagramei de momente incovoietoare de pe
portiunea o-x fata de origine,
deci 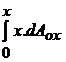 = a1 Aox ; unde x = a1 + a2
= a1 Aox ; unde x = a1 + a2
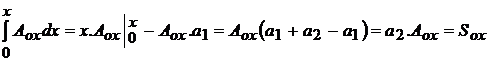 .
.
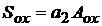 reprezinta
momentul static al suprafetei
reprezinta
momentul static al suprafetei
diagramei de momente incovoietoare de pe
portiunea o-x fata de sectiunea ( x ) .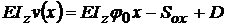 ; constanta( D ) se afla din conditia
initiala a lui Cauchy :
; constanta( D ) se afla din conditia
initiala a lui Cauchy : 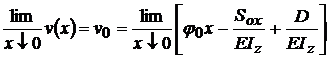 ;
; 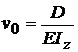 ;
;
D
= v0 . E
Iz ; 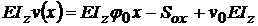 .
.
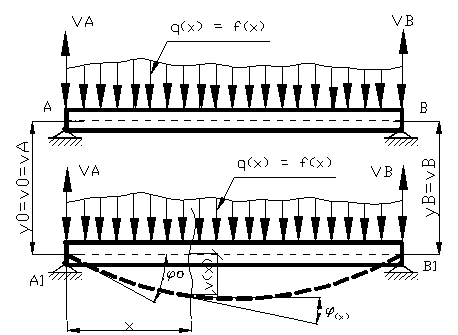
Figura 17
Aceasta metoda este o
combinatie intre metoda grafica si cea analitica , dar
pentru expresii mai dificile ale sarcinii distribuite de incarcare q(x) = f(x), devine mai greu de aplicat, metoda aceasta ajuta la demonstrarea
ecuatiei celor trei momente ( ecuatia
lui Clapeyron ) , care este folosita la rezolvarea grinzilor
continuie.
Problema nr. 7
Sa
se calculeze sageata si rotirea sectiunii transversale din punctul
Q ,pentru bara din figura 20, stiind ca : E = 2,1 .105 N/mm2; l = 0,43 m avand
sectiunea transversala circulara inelara cu d=40 mm si
D = 50 mm.
Rezolvare:
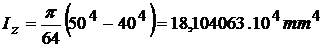 ;
;
Aflam
fortele de reactiune VA si VB din conditiile
de echilibru:
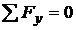 ; VA - 1 kN + VB = 0 ; ecuatia de verificare.
; VA - 1 kN + VB = 0 ; ecuatia de verificare.
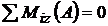 ;
; 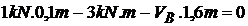 ;
;
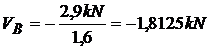 ;
;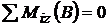
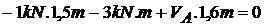 ;
; 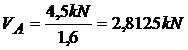 ;
;
VA - 1 kN + VB = 0 ; ecuatia de verificare, 2,8125
kN - 1 kN - 1,8125 kN = 0 ; 0 = 0 este indeplinita ecuatia de
verificare , deci s-au calculat corect fortele de reactiune .
Deoarece VB = - 1,8125 kN , se
schimba sensul, acest lucru nu este
obligatoriu.
Regiunea
intai
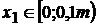 ;
; 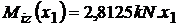 ;
; 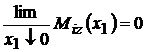 ;
;

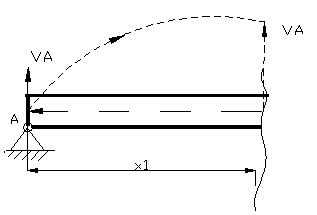
Figura 18
Regiunea a II-a
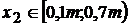 ;
; 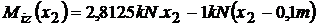 ;
;
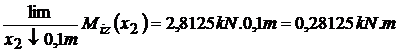 ;
;
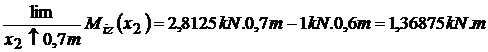
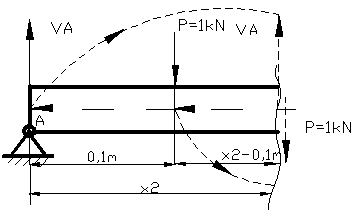
Figura
19
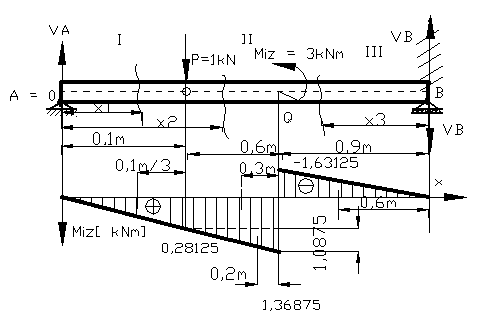
Figura
20
Regiunea
a III-a
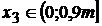 ;
; 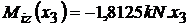 ;
;
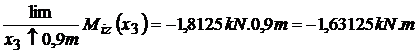 ;
;
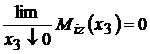 .
.
Se ia ca origine unul din capetele barei A - O, aceasta origine trebuie sa
ramana neschimbata pe tot timpul rezolvarii problemei.
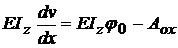 ;
; 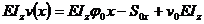 ; dar v0 = 0 in cazul
nostru,
; dar v0 = 0 in cazul
nostru, 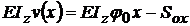 ; pentru a afla pe φ0 ( rotirea sectiunii transversale in
origine ) folosim a II-a conditie de reazem, anume sageata in B este egala cu zero ( vB = 0 ) .
; pentru a afla pe φ0 ( rotirea sectiunii transversale in
origine ) folosim a II-a conditie de reazem, anume sageata in B este egala cu zero ( vB = 0 ) . 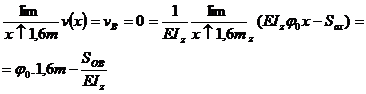
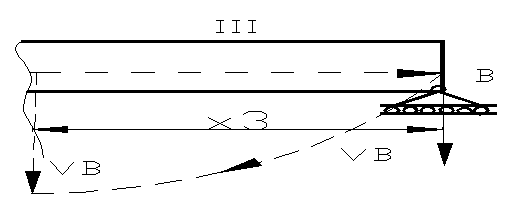
Figura
21
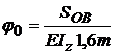 .
.
S-a desfacut
trapezul dreptunghic intr-un triunghi si un dreptunghi, conform
principiului suprapunerii efectelor.
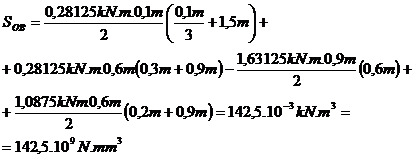
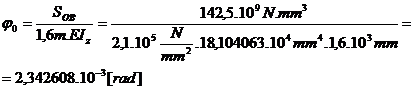 .
.
Pentru a afla
sageata si rotirea sectiunii transversale din punctul Q , trebuie sa tinem cont de originea
care se afla in A= O.
 ; pentru Q avem
:
; pentru Q avem
:
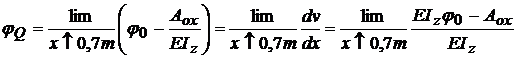 ;
; 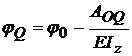 ;
;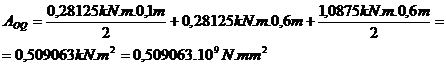
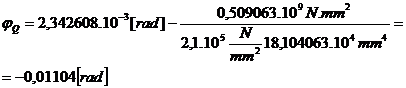 ;
;
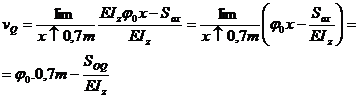 ;
;
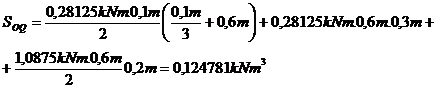 ;
;
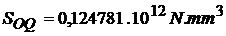 ;
;
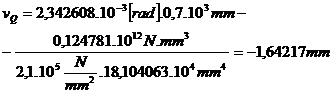
Problema nr.8
Sa se calculeze
sageata si rotirea sectiunii transversale din punctul Q , pentru
bara din figura 22 , stiind ca :
E = 2,1.105
N/mm2 ; P = 2 kN ; l = 0,63 m cu sectiunea
transversala din figura 23.
Rezolvare:
Aflam
fortele de raectiune VA si VB din conditiile de echilibru:
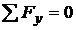 ; VA + VB = P ; ecuatia de verificare.
; VA + VB = P ; ecuatia de verificare.
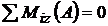 ; P.l - VB .4l = 0 ;
; P.l - VB .4l = 0 ; 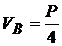 .
.

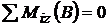 ; -3l. P. + VA .4l = 0 ;
; -3l. P. + VA .4l = 0 ; 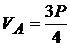 ; ;
; ;
VA + VB
= P ; ecuatia de verificare ; 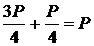 ; P = P , este indeplinita
ecuatia de verificare, deci s-au calculat corect fortele de
reactiune .
; P = P , este indeplinita
ecuatia de verificare, deci s-au calculat corect fortele de
reactiune .
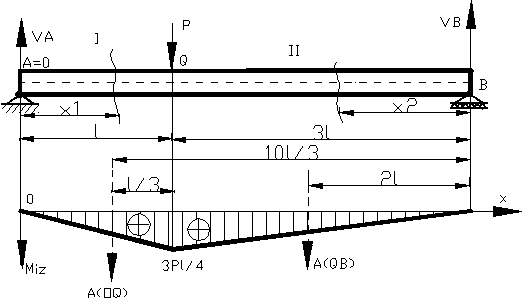
Figura 22
Se calculeaza
mai intai caracteristicile sectiunii transversale, apoi se calculeaza
si celelalte date ale problemei.
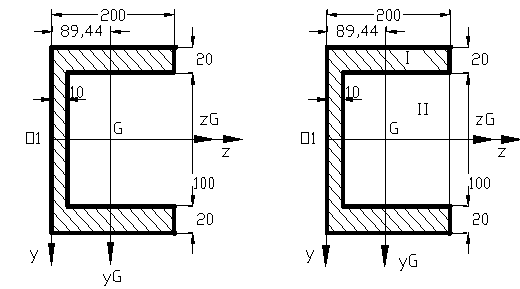
Figura 23


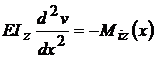 ; prin integrare se
va obtine,
; prin integrare se
va obtine, 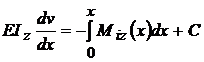 ;
; 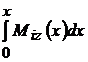 = Aox ,
reprezinta aria diagramei de
= Aox ,
reprezinta aria diagramei de
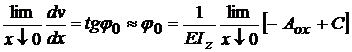 ;
; 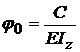 ;
; 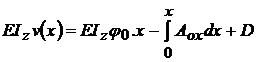 .
.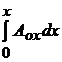 ; f ( x ) = Aox ;
; f ( x ) = Aox ; 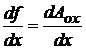 ; dg = dx ;
; dg = dx ; 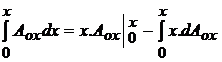 ; cum din figura
16 , reiese ca
; cum din figura
16 , reiese ca 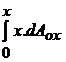 reprezinta momentul static al suprafetei
reprezinta momentul static al suprafetei 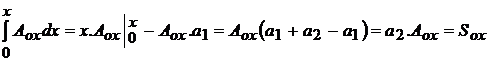 .
.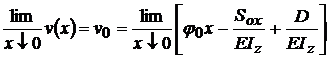 ;
; 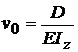 ;
; 
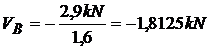 ;
;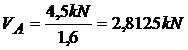 ;
;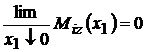 ;
; 

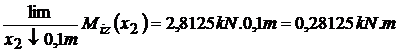 ;
; 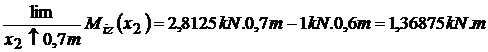


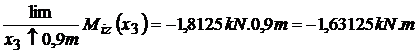 ;
; 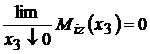 .
.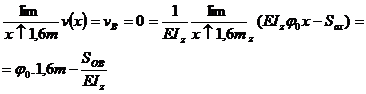

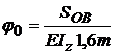 .
.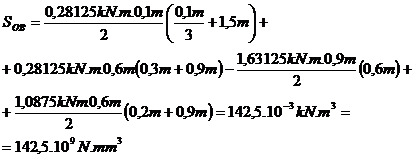
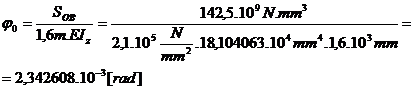 .
. ; pentru Q avem
:
; pentru Q avem
: 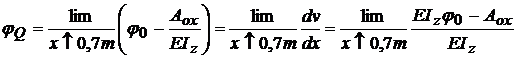 ;
; 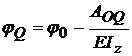 ;
;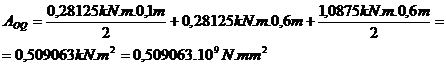
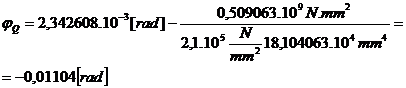 ;
;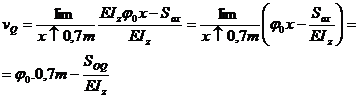 ;
; 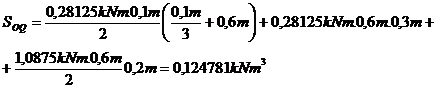 ;
;