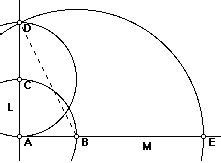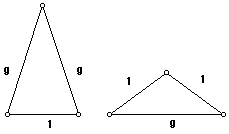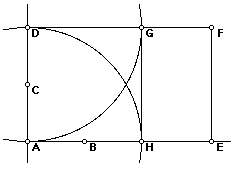Sectiunea de aur - matematica

SECTIUNEA DE AUR - MATEMATICA

Celebrul arhitect Le Corbusier a preconizat in epoca notiunea de "modulor". Aceasta notiune se inrudeste,in mod ciudat, cu matematica. Cuvantul in sine deriva de la "modul"(raport sau scara de proportie) si or(aur). Se intelege ca e vorba de un raport intre doua marimi-doua segmente; astfel termenul misterios se transforma intr-o notiune deja cunoscuta : modulul de aur,raportul sau sectiunea de aur,acel raport caruia ,pe vremuri Fra Luca Pacioli di Borgo i-a spus proportia divina si a folosit denumirea ca titlu pentru cartea tiparita in 1509 la Venetia,la insistenta prietenului sau Leonardo da Vinci,care a si ilustrat-o. Le Corbusier nu face altceva decat sa reia, in 1950, problema pusa de inaintasul lui cu aproximativ 450 de ani in urma, publicand, de data asta la Paris,o carte cu titlu asemanator :"Le modulor. Essai sur une mesure harmonique a l'echelle humaine applicable universelement a l'architecture et a la mecanique"

Canonul sectiunii de aur era cu strictete respectat de vechii greci in epoca lui Pericle dar denumirea are o datare mai recenta. Se pare ca denumirea sectio aurea se datoreaza lui Leonardo da Vinci dar ea nu era folosita nici atunci in mod curent, ci de-abia de pe la inceputul secolului al XIX-lea . Geometrii greci de dinaintea lui Euclid , ca Pitagora si, Eudoxus,Platon I-au spus pur si simplu raport. Euclid e primul care il denumeste raport extrem si mediu ,deosebindu-l astfel de toate celelalte rapoarte in care s-ar putea imparti un segment de dreapta.

Se pare ca,l atunci cand segmentele b si c sunt in sectiune de aur ele plac ochiului mai mult decat daca s-ar fi impartit aceeasi lungime in oricare alte segmente neegale b',c'. Aceeasi observatie empirica l-a condus pe Leonardo da Vinci sa numeasca sectio aurea , adica "sectiunea de aur", impartirea segmentului de lungime a in segmentele b si c (a/b=b/c).El sustine misterul acestei sectiuni si aduce exemple luate din proportiile diferitelor parti ale corpului omenesc sau din arhitectura,afirmand ca forma armonioasa a corpului omenesc se explica prin existenta acestui raport de aur intre diferitele parti ale lui. Astfel buricul imparte lungimea corpu;ui omenesc dupa sectiunea de aur . Toate statuile antice sunt construite dupa aceasta regula. Mai mult , Leonarda da Vinci e de parere ca sectiunea de aur este canonul dupa care ar trebui sa se stabileasca proportiile dintre diferitele parti ale aceleiasi cladiri, precum si intre volumul construit si cel ramas liber, pentru ca numai astfel poate sa placa ochiului.Luca Pacioli, mai mistic din fire , a numit acest raport divina proportione si a incercat sa justifice titulatura printr-o multime de analogii si comparatii metafizice luate fie din filozofia lui Platon ,fie din teologia crestina.Iata un exemplu: " . Dupa cum Dumnezeu nu poate fi dovedit prin cuvinte , tot asa nici acest raport nu poate fi definit printr-un numar rational ci ramane totdeauna ascuns si secret si de aceea este numit de matematicieni iartional". Pe atunci numerele irationale erau inca o enigma a matematicienilor . De aceea o parere asemanatoare vom intalni pe tot parcursul secolului al XVI-lea si,de pilda , marele astronom Kepler scria :"Aceasta proportie geometrica,cred eu , a fost pentru creator o idee care ramane singura vesnica pentru a releva crearea celui asemenea din cel asemenea . "

Preferinta pentru raportul de aur a starnit curiozitatea cercetatorilor din secolul XIX, care curiosi sa gaseasca un motiv acestei preferinte,au facut multe anchete statistice in diferite domenii.Astfel , un cunoscut psiholog de atunci, G. Th. Fechner, a prezentat unui larg public o serie de dreptunghiuri de dimensiuni diferite si a cerut sa se aleaga cele cu forma cea mai placuta.Majoritatea preferintelor au fost pentru dreptunghiurile cu dimensiunile in taietura de aur. De altfel forma obisnuita a cartilor ,a meselor si a multor obiecte dreptunghiulare de uz curent , e astfel proportionata.S-au mai facut masuratori pentru a se vedea daca acest raport se intalneste in natura, intre diferitele parti ale corpului omenesc, ale plantelor sau ale animalelor.Acestea au dus cu gandul la Sirul lui Fibonacci , sau asa numita lege a cresterii organice.

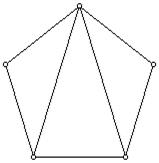
CONSTRUCTIA SEGMENTULUI DE AUR:

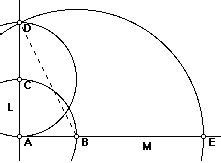
Gheorghe Titeica , marele nostru savant, spunea, vorbind despre sectiunea de aur, ca stramosii nostrii cei mai indepartati "aveau in instinct simtul proportiei si cunosteau, fara sa fi invatat vreodata, proprietatile figurilor asemenea".

Ca segmentele ale caror lungimi sunt in sectiune de aur starnesc instinctiv sentimentul de armonie, au observat-o multi. Exemplul cel mai cunoscut si plastic totodata este linia care desparte marea de cer. Aceasta linie nu e niciodata asezata la mijloc, ea e asezata in asa fel incat grosimea celor doua benzi sa fie una fata de alta in raportul sectiunii de aur. Acest exemplu il alege si Timerding :"Ochiul - spunea el- comparand grosimea benzii mai inguste cu a celeia mai late, taie in gand o grosime din banda lata cat este grosimea celei inguste si atunci obtine o banda care satisface aceeasi proportie, de unde impresia de repaus, de constanta , de siguranta, intr-un ritm continuat in mod nedefinit! Sectiunea de aur se impune deci ori de cate ori doua parti consecutive fac parte, printr-o noua subdiviziune, dintr-o progresie geometrica, reunind astfel triplul efect al echipartitiei , al succesiunii si al proportiei continue . Folosirea sectiunii de aur nu-i decat un caz particular al unei reguli generale , a aceleia de revenire la aceeasi proportie, in detaliile unui ansamblu".

O alta proprietate oarecum ciudata a raportului de aur e ca daca scadem din primul segment pe cel de al doilea segmentul obtinut se afla si el in raport de aur.Astfel rezulta un sir de segmente ce se scand unele din altele la nesfarsit si de aici proprietatea de incomensurabilitate a segmentelor aflate in taietura de aur. Nu ar trebui sa ne sperie aceasta proprietate, precum afirma Euclid in Cartea a X-a a Elementelor " Se numesc marimi comensurabile acelea care se pot masura cu aceeasi masura, iar incomensurabile cele pentru care nu se poate afla o masura comuna".

Scriem proportia de aur sub forma a/b=b/c si alegem ca unitate de masura a acestor segmente segmentul cel mai mic si anume c . Raportul b/c fintre partea cea mai mare si partea cea mai mica a segmentului a , se numeste numar de aur si se noteaza cu . Rezulta atunci ca :

a/b=b/c= si pentru ca a=b+c  rezulta ca

(b+c)/b=1+c/b=b/c adica 1+1/

De aici considerand numai radacina pozitiva avem care se aproximeaza la 1,618.

NUMARUL DE AUR SI SIRUL LUI FIBONACCI :

1+

si de aici inmultim succesiv cu ³ . obtinem o progresie geometrica de ratia ;mai mult orice termen al progresiei e egal cu suma celor doi termeni precedenti; termenii sirului 1, ³ . au proprietati aditive si totodata multiplicative. De aici

asemanarea cu sirul lui Fibonacci. Pe masura ce sirul continua , raportul dintre termenul n si cel precedent lui(termenul n-1) se apropie de 1.618033989..

Acest sir e dublu aditiv si, dupa cate se pare , are calitatea de a reflecta numeric o insusire a materiei vii, aceea a cresterii realizate prin compuneri succesiv aditive. De exemplu botanistii au gasit ca pe o tulpina, distantele dintre nodurile de unde se dezvolta frunzele sunt repartizate aproximativ dupa aceasta lege. Aproximativ pentru ca in procesul de dezvoltare a unei plante sau a unui animal apar uneori si conditii particulare legate de sol, de clima sau de alti factori, imposibil de determinat care pot influenta cresterea si dezvoltarea intr-un mod anormal. Proprietatea de dublu aditivitate trebuie privita statistic, adica in medie la un numar mare de masuratori. Numai astfel se poate afirma ca masuratorile duc la aceasta concluzie. De asemenea se remarca aceasta lege de crestere in forma cochiliilor melcilor, sau a scoicilor, a coarnelor animalelor, a unor oase, cum ar fi femurul la om, unde, desi cresterea se face numai printr-o extremitate, se pastreaza forma initiala , transformandu-se in una mai mare asemenea ei.

Cochilia melcului desi pare ca nu ascunde nici un mister are forma spiralei logaritmice. Proprietatile spiralei logaritmice sunt oarecum ciudate. Daca intersectam spirala cu o dreapta dusa prin centru si apoi ducem tangente in punctele de intersectie, unchiul facut de tangente cu raza va fi constant q. Proprietate care o inrudeste cu cercul , iar daca unghiul q ar avea 90 atunci spirala se inchide, transformandu-se in cerc. Dar mai important e ca segmentele determinate de fiecare spira pe raza sunt in sectiune de aur. Spirala logaritmica nu s-a nascut din imaginatia matematicienilor ci din pulsatia vietii, din crestere regulata prin adaugarea de elemente asemenea si are proprietatea ca e asemenea cu ea insasi. Daca vrem sa marim sau sa micsoram o spirala logaritmica ca s-o transformam in una asemenea ei, regasim aceeasi spirala de la care am pornit rotita fata de prima cu un anumit unghi. Jacob Bernoulli a ramas asa de incantat si de uimit de aceasta proprietate pe care a descoperit-o chiar el prin 1680, incat a cerut ca, pe piatra mormantului sa-i fie sapata spirala logaritmica cu inscriptia :"Eadem mutata resurgo" adica :" Ma transform ,ramanand aceeasi.". Ciudat este ca pana si ochiurile unui paun ,cand acesta isi desface coada in toata splendoarea ei, se aseaza dupa doua spirale logaritmice.Constructia spiralei are la baza tot raportul de aur. Pentru a construi spirala de aur avem intai nevoie de tringhiul, respectiv dreptunghiul de aur .

CONSTRUCTIA TRIUNGHIULUI DE AUR:

DEFINITIE: (definitia nu e data in terminologia standard): Un triunghi de aur ascutit-unghic este un triunghi isoscel, cu laturile congruente mai lungi decat baza si care formeaza un raport de aur cu aceasta. Un triunghi de aur optuz-unghic este un triunghi isoscel, cu laturile congruente mai scurte decat baza si care formeaza cu aceasta un raport de aur.

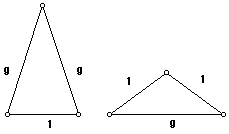
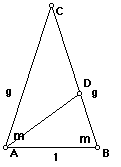
` PROPRIETATILE TRIUNGHIULUI DE AUR:

Fie D un punct pe BC astfel incat AD = 1. Dreapta AD imparte triunghiul ABC in 2 triunghiuri mai mici : ABD si ADB. Deoarece AD = AB = 1 => < ABD = < ADB = m (unde cu < este simbolul pentru unghi). Se demonstreaza usor ca triunghiul ABD este asemenea lui ABC, si folosind proportiile si segmentul de aur, ca BD = g-1. In concluzie CD = 1. Se poate afla si ungiul m ce caracterizeaza tringhiurile de aur.

Se poate observa deci ca un triunghi de aur (ABC) se poate imparti in doua triunghiuri de aur (ACD si ABD). Proprietatea este valabila si in cazul triunghiului optuz-unghic.

CONSTRUCTIA DREPTUNGHIULUI DE AUR:

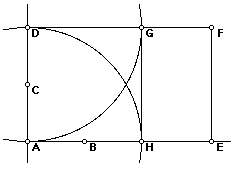
CONSTRUCTIA SPIRALEI LOGARITMICE:

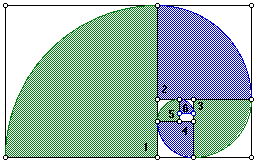
CONSTRUCTIA PENTAGONULUI:

METODA 1.

METODA 2.

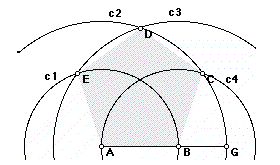
Natura si sectiunea de aur par legate, ca si cum sectiunea aceasta ar fi parte din natura.Armonia nu-i altceva decat coexistenta normala si deci fericita a lucrurilor sau a fiintelor. Reprodus de mii si mii de ori de-a lungul mileniilor, in diferite forme din lumea plantelor si animalelor, ochiul omenesc s-a deprins raportul taieturii de aur din mosi-stramosi si de aceea ii place instinctiv, fara sa mai intrebe de ce. Tot asa s-a obisnuit cu planul de simetrie vertical pe care il vede in corpul lui sau al celorlalte animale si uneori al plantelor. Nici un artist nu ar indrazni sa introduca intr-un monument un plan de simetrie orizontal. La fel si in arhitectura; lasand deoparte detaliile de decorare a suprafetelor cladite, ochiul omenesc este influentat, in primul rand, de raportul dintre volumul construit si acela al spatiului care il adaposteste. Modul de repartitie al greutatilor va starni in el sentimentul frumosului, al echilibrului, al armoniei, sau nu. Vitruviu atragea atentia, in cartea lui despre arhitectura, atat asupra acordului care trebuie stabilit intre partile unei cladiri cat si ale acestora fata de ansamblu.

Oare modulorul lui Le Corbusier detine secretul armoniei??? Eu asa cred. Luand omul ca etalon, asa cum au facut-o de altfel si in antichitate, dar folosind o alta lege a cresterii organice, aceea care i-a permis sa afle numarul de aur corespunzator dimensiunilor cerute de epoca moderna, el a stabilit o noua scara de proportii, pe care o numeste modulor. Modulorul are toate sansele sa redea arhitecturii armonia corespunzatoare noilor conditii, pastrand totodata caracterul seninatatii interioare din operele clasice. Grija de capetenie a lui Le Corbusier a fost ca, schimband etalonul sa tina seama, in distributia dimensiunilor, de acelasi raport al sectiunii de aur. Etalonul lui Le Corbusier este un segment egal cu inaltimea unui om mijlociu stand in picioare si avand un brat un brat ridicat, adica 216 cm. In acest caz, ombilicul imparte acest segment in doua parti egale de 108 cm. Tinand seama ca unul dintre cele doua segmente de 108 cm este impartit(aproximativ) in sectiunea de aur prin lungimea de la varful degetelor la cap(41.5) si de la cap la ombilic (66.5), se formeaza astfel un sir aditiv :

41.5 . .

care reprezinta scara modulor.

Totusi Le Corbusier are grija sa atraga atentia asupra unui fapt spunand:

"Modulorul nu da talentul si, inca mai putin, geniul. El nu subtiaza ceea ce nu-i subtire; el ofera doar placerea si increderea care poate rezulta din folosirea masurilor sigure". Arta cere ceva mai mult decat selectivitate, abilitate, organizare sau principii descoperite si formulate matematic. Modulorul ramane un instrument, o dalta in mana sculptorului care va realiza opera.

Se pare, din spusele unora, ca si piramida lui Keops are legatura cu numarul de aur. Unii cercetatori pretind ca toate cunostiintele matematice ale egiptenilor stau inscrise in piatra si anume ca ele pot fi gasite in dimensiunile marii piramide. Analizand masuratorile facute de geodezi si de astronomi asupra marimii sau orientarii piramidei lui Keops, ei au dedus ca egiptenii cunosteau cu exactitate nu numai dimensiunile Pamantului si distanta lui pana la Soare, ba chiar si valoarea lui p, cu aceeasi aproximatie cu care o stim si noi. Dar ultima afirmatie contrazice chiar faptele care se gasesc in manuscrisele ramase de atunci, din care reiese ca egiptenii considerau p=3.16 si nu aproximativ p=3.14. Egiptenii cunosteau proprietatile estetice ale raportului dintre doua segmente aflate in taietura de aur si se foloseau de el cand stabileau dimensiunile cladirilor si ale piramidelor. Astfel Herodot povesteste ca preotii egiptenii i-au destainuit ca aria fiecarui triunghi lateral al piramidei este egala cu patratul inaltimii piramidei. Dar, cum profilul meridian al marii piramide este un triunghi dreptunghic rezulta ca laturile (a,b,c) sunt in progresie geometrica : a/b=b/c. Insa fiind vorba de un triunghi dreptunghic, rezulta, din teorema lui Pitagora, ca a²=b²+c² sau, impartind prin c :

(a/c =(b/c)²+1

dar b²=ac; asadar ecuatia devine (a/c)²=1+a/c;

si notand a/c= , avem

Deci laturile acestui triunghi dreptunghic se afla in sectiune de aur, iar numarul =a/c reprezinta raportul dintre ipotenuza si cateta cea mai mica. Din intamplare valoarea aproximativa a lui este foarte apropiata de aceea, tot aproximativa a lui p. Valorile sunt:

=1.272 si 4/p

1/ =0.618 si (p

Valorile extrem de apropiate au dus la confuzia creata intre p si raportul de aur. Matematicianul francez Paul Montel intr-un articol publicat in "Comptes rendus" din paris arata ca din punct de vedere matematic e imposibil ca egiptenii sa fi ingramadit in dimensiunile unei piramide atatea date stiintifice diferite, cate se sustin ca ar rezulta din masuratorile facute de unii dintre entuziastii egiptologi. Singura valoare pe care egiptenii au "gravat-o" cu adevarat in piramida lui Keops este aceea a sectiunii de aur, construind triunghiul dreptunghic meridian cu laturile in acest raport. De aceea acest triunghi poarta numele de triunghi egiptean. Mai cunoscut decat acesta si cu acelasi nume este un alt triunghi dreptunghic si anume acela cu laturile proportionale cu 3, 4, 5. Si acesta a fost folosit de egipteni. El se gaseste in semiprofilul altei piramide din Gizeh. Fiind insa si singurul triunghi dreptunghic in care laturile sunt in progresie aritmetica, el se numeste triunghiul egiptean perfect. Cel mai probabil este ca grecii au luat notiunea sectiunii de aur de la egipteni. Nimic nu este sigur dar din diferite surse antice reiese clar ca pitagoricienii cunosteau numerele irationale si sectiunea de aur. Prima si cea mai veche relatare e cea a lui Platon. In Timeu, el arata ca pitagoricienii dadeau o deosebita atentie studiului celor cinci poliedre regulate convexe. Chiar Platon scrie in Timeu:" tetraedrul, simbolul focului, fetele lui sunt 4 triunghiuri echilaterale;cubul are 6 fete patrate si e simbolul pamantului;octaedrul, marginit de 8 triunghiuri echilaterale, este simbolul aerului;icosaedrul, cu 20 de triunghiuri echilaterale ca fete, este simbolul apei si in fine, dodecaedrul, simbol al cosmosului cu tot ce cuprinde el, este singurul poliedru regulat cu fete formate din pentagoane in numar de 12 si nu din triunghiuri sau patrate". De aici vine si termenul chintesenta ( quintaesentia ) ce s-a adaugat la cele patru "elemente" : aerul, apa, pamantul si focul. Acest simbolism are o explicatie : Platon, ca si alti filozofi din antichitate, considera ca focul, pamantul, aerul si apa sunt elemente primordiale, atomii din combinarea carora s-a format universul si tot ce exista in el; anume, 3 dintre ele erau imaginea tipica a starilor in care se manifesta materia: solida-pamantul, lichida-apa si gazoasa-aerul, iar focul era imaginea energiei. Iar cum Platon era un mare admirator al geometriei, a cautat o corespondenta, o analogie de natura geometrica, pentru aceste elemente si ea i-a fost sugerata de cele cinci poliedre regulate pe care le-a studiat in scoala lui Pitagora. Astfel, datorita formei lor remarcabile, aceste elemente au devenit simbolurile "elementelor". Cele patru poliedre regulate cu suprafata compusa din triunghiuri sau patrate au devenit simbolul celor patru elemente iar dodecaedrul, cu forma sa aproape sferica, din care cauza i se si spunea sfera facuta din 12 pentagoane regulate, a fost considerata ca evocand insasi sfera cereasca, imaginea universului intreg. Asadar de la Platon avem cea mai veche marturie despre cunoasterea sectiunii de aur de catre pitagoricieni. A doua marturie e cea a lui Iamblic din Calcida, care a trait pe la sfarsitul secolului al III-lea si inceputurile celui de-al IV-lea. El a scris mai multe carti despre viata si operele pitagoricienilor. In cele ce au ajuns pana in zilele noastre se mentioneaza faptul ca Hippasus din Metapont, elev din scoala lui Pitagora, a pierit intr-un naufragiu, pedepsit fiind de zei pentru ca s-a laudat cu decoperirea dodecaedrului.