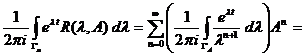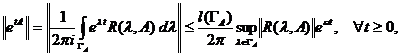Indici de crestere asociati unui 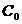 - semigrup
- semigrup
Fie X un spatiu Banach peste K, unde K  . Fie S
=
. Fie S
= 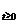 un
un 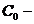 semigrup pe X, iar
A : D(A)
semigrup pe X, iar
A : D(A) 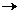 X generatorul
sau infinitezimal. Pe D(A) vom considera norma de grafic inchis, definita
prin
X generatorul
sau infinitezimal. Pe D(A) vom considera norma de grafic inchis, definita
prin
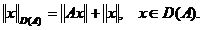
Consideram
multimile
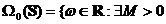 astfel incat
astfel incat 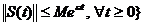
si
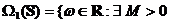 astfel incat
astfel incat 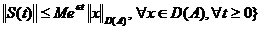 .
.
Remarca 1. Din Teorema I.1.1.
rezulta imediat ca 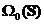
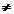 Ř.
Ř.
Propozitia 1. 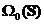
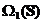 .
.
Demonstratie. Fie 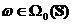 . Atunci exista M > 0 astfel incat :
. Atunci exista M > 0 astfel incat :
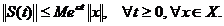
In particular,
daca 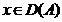 , tinand seama ca
, tinand seama ca 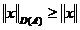 se obtine ca
se obtine ca
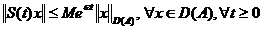 ,
,
adica 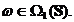 Deducem de aici
ca
Deducem de aici
ca 
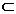
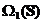 .
.
Remarca 2. Din
Propozitia 1. si Remarca 1. rezulta ca 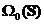
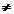 Ř.
Ř.
Consideram
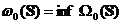
si respectiv
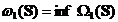 .
.
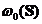 se numeste indicele
de crestere uniforma al semigrupului S, iar
se numeste indicele
de crestere uniforma al semigrupului S, iar
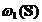 se numeste indicele
de crestere marginita al semigrupului S.
se numeste indicele
de crestere marginita al semigrupului S.
Remarca 3. Din Propozitia 1. rezulta ca 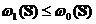 .
.
Vom prezenta in continuare, diverse
formule de calcul pentru indicii de crestere introdusi mai sus.
Teorema 1. Daca 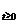 este un
este un 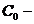 semigrup atunci
semigrup atunci
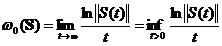 .
.
Vom demonstra
pentru inceput ca 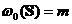 .
.
Fie 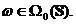 Atunci exista M
> 0 astfel incat
Atunci exista M
> 0 astfel incat
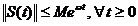 .
.
Prin logaritmare
inegalitatea devine
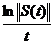
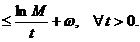
De aici
rezulta ca
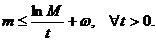
de unde
obtinem 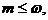 pentru orice
pentru orice 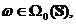 adica
adica 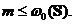
Reciproc, fie 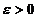 . Atunci exista
. Atunci exista 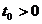 astfel incat
astfel incat
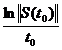 <
<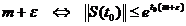 .
.
Fie 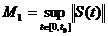 . Pentru orice t > 0 exista un unic
. Pentru orice t > 0 exista un unic 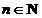 astfel incat
astfel incat 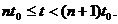 De aici avem ca
De aici avem ca
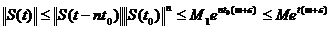
unde 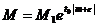 . Am aratat in acest mod ca pentru orice
. Am aratat in acest mod ca pentru orice 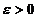 exista M
> 0 astfel incat
exista M
> 0 astfel incat
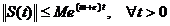 (1.5)
(1.5)
adica 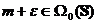 . Obtinem de aici ca
. Obtinem de aici ca
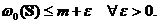
Deci 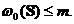 In concluzie
In concluzie 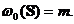
Fie acuma 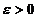 . Conform relatiei (1.5) exista M > 0
astfel incat
. Conform relatiei (1.5) exista M > 0
astfel incat
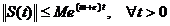
Asadar
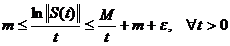 (1.6)
(1.6)
Trecand la limita in
relatia (1.6) obtinem imediat ca
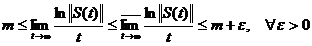 .
.
Rezulta
ca exista
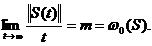
Fie S = 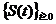 un
un 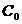 - semigrup si A generatorul sau infinitesimal.
- semigrup si A generatorul sau infinitesimal.
Definitia 1. Multimea
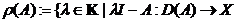 este bijectiv si inversul sau
este bijectiv si inversul sau
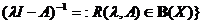
se numeste multimea rezolventa a operatorului A,
iar 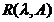 se numeste aplicatia
rezolventa in punctul
se numeste aplicatia
rezolventa in punctul 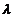 .
.
Definitia 2. Multimea
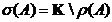
se numeste spectrul operatorului A, iar numarul
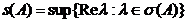
se numeste supremumul realului spectrului operatorului A.
Remarca 4. Multimea
rezolventa este o multime deschisa , iar spectrul este o
multime inchisa.
In cele ce urmeaza vom prezenta o
teorema de caracterizare pentru 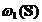 si legatura
acestuia cu
si legatura
acestuia cu 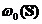 , respectiv cu s(A).
, respectiv cu s(A).
Fie 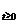 un
un 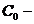 semigrup pe un spatiu Banach X, iar A generatorul sau
infinitezimal. Consideram multimea :
semigrup pe un spatiu Banach X, iar A generatorul sau
infinitezimal. Consideram multimea :
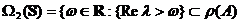 si
si
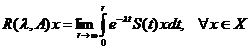 si
si 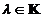 cu
cu 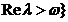 .
.
Teorema 2. 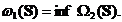 In plus
In plus
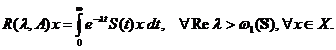
Demonstratie. Vom
demonstra ca 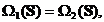 in trei etape.
in trei etape.
ETAPA 1. Aratam
ca daca 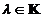 si pentru orice
si pentru orice 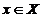 exista
exista
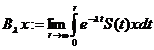
atunci 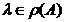 si
si 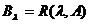 .
.
Intr-adevar, fie 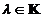 cu proprietatea
ca pentru orice
cu proprietatea
ca pentru orice 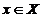 exista
exista
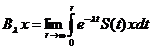 .
.
Sa observam
ca pentru fiecare 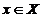 si fiecare t > 0 avem succesiv
si fiecare t > 0 avem succesiv
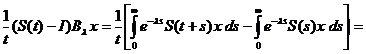
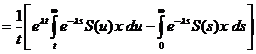 =
=
=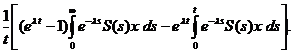
Trecand la limita pentru 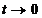 deducem ca
deducem ca 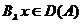 si
si 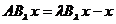
deci
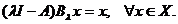 (1.7)
(1.7)
Fie acum 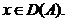 Observam ca
Observam ca
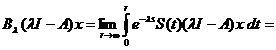
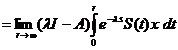 . (1.8)
. (1.8)
Notam cu
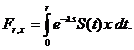
Atunci 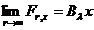 si conform (1.8)
deducem ca
si conform (1.8)
deducem ca
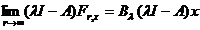
Din faptul ca A este un operator inchis, rezulta ca 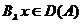 si
si
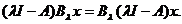
Atunci din (1.7) avem ca
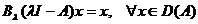 (1.9)
(1.9)
Am demonstrat in
acest mod ca (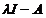 ) este inversabil si ca
) este inversabil si ca 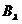 este inversul sau.
este inversul sau.
Fie 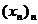 cu
cu 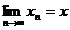 si
si 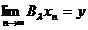 . Notam cu
. Notam cu 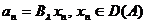 , oricare ar fi
, oricare ar fi 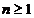 . Atunci
. Atunci 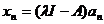 , pentru orice
, pentru orice 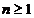 .
.
Asadar 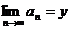 si
si
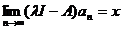 .
.
Cum A este inchis
deducem de aici ca 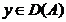 si
si 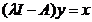 . Rezulta ca
. Rezulta ca 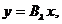 deci
deci 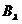 este inchis . Conform Principiului graficului inchis
obtinem ca
este inchis . Conform Principiului graficului inchis
obtinem ca 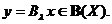 Rezulta ca
Rezulta ca 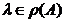 si
si 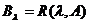 , deci prima etapa este demonstrata.
, deci prima etapa este demonstrata.
Din aceasta etapa deducem
ca 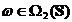 daca si numai
daca pentru orice
daca si numai
daca pentru orice 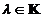 cu
cu 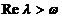 si orice
si orice 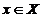 exista
exista 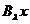 .
.
ETAPA 2. 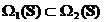 .
.
Fie 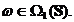 Atunci exista
Atunci exista 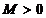 astfel incat
astfel incat
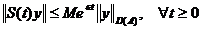 si
si 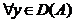 .
.
Demonstram ca oricare ar
fi 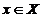 si
si 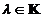 cu
cu 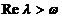
 exista
exista
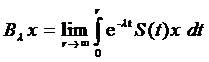 .
.
Pentru aceasta consideram
urmatoarele cazuri :
CAZUL I. Presupunem ca  Atunci, pentru orice
Atunci, pentru orice 
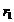 , avem
, avem
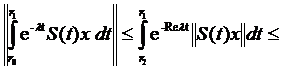
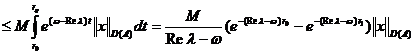
Din
relatia de mai sus rezulta ca pentru orice  exista c > 0 astfel incat
exista c > 0 astfel incat
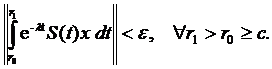
De
aici, deducem ca exista
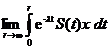 .
.
CAZUL II. Fie 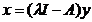 cu
cu 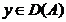 . Atunci, oricare ar fi r > 0 avem
. Atunci, oricare ar fi r > 0 avem
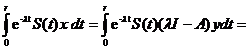
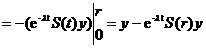 .
.
Din
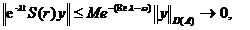 pentru
pentru 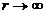
deducem ca
exista
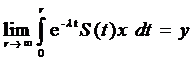 .
.
CAZUL III. Fie 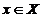 si
si 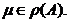 Din identitatea
rezolventei
Din identitatea
rezolventei
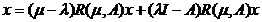
si din
cazurile anterioare se obtine ca exista 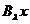 .
.
Din demonstratia de mai sus si din Etapa 1, rezulta
ca 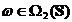 .
.
ETAPA 3. 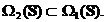
Fie 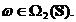 Atunci
Atunci 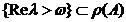 si
si
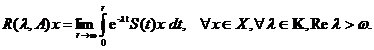
Fie 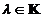 cu
cu 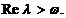 Analog ca an ETAPA 2,
Cazul II, avem ca
Analog ca an ETAPA 2,
Cazul II, avem ca
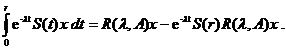
Rezulta
ca aici exista 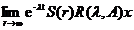 , oricare ar fi
, oricare ar fi 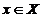 . Prin urmare exista
. Prin urmare exista 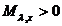 astfel incat
astfel incat
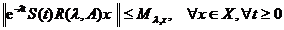 .
.
Din Principiul marginirii
uniforme deducem ca exista 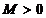 astfel incat
astfel incat
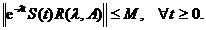
Asadar
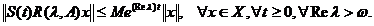
Fie 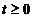 si
si 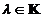 cu
cu 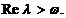 Daca
Daca 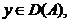 atunci
atunci
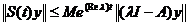 .
.
Cum
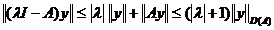
obtinem
ca
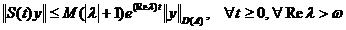 .
.
Pentru 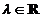 , facand
, facand 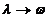 obtinem :
obtinem :
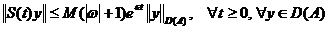 .
.
Rezulta
ca 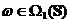 , deci
, deci 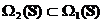 . In
concluzie, am obtinut ca
. In
concluzie, am obtinut ca
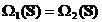 . (1.9)
. (1.9)
Din (1.9) rezulta 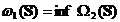 .
.
Corolarul 1. Pentru un 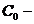 semigrup cu generatorul infinitezimal A avem
semigrup cu generatorul infinitezimal A avem
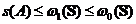 .
.
Demonstratie. Am vazut ca 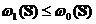 . Din Teorema 2. rezulta ca oricare ar fi
. Din Teorema 2. rezulta ca oricare ar fi 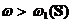 avem
avem 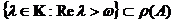 .
.
Asadar
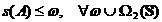 .
.
Prin urmare
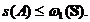
Exercitiul 1. Fie S = 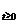 un
un 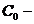 semigrup pe
spatiul Banach X , iar A generatorul sau infinitesimal.
Sa se arate ca :
semigrup pe
spatiul Banach X , iar A generatorul sau infinitesimal.
Sa se arate ca :
(i)
daca
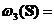
atunci 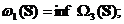
(ii) daca
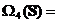
atunci 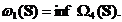
Fie
S = 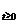 un
un 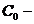 semigrup pe
spatiul Banach X cu generatorul infinitezimal
semigrup pe
spatiul Banach X cu generatorul infinitezimal 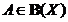 .
.
Definitia 3. Numarul
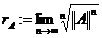
se numeste raza
spectrala a operatorului A.
Remarca 5. 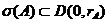 adica
spectrul este continut in discul deschis centrat in origine si de raza
egala cu raza spectrala.
adica
spectrul este continut in discul deschis centrat in origine si de raza
egala cu raza spectrala.
In continuare, vom demonstra ca in cazul
semigrupurilor generate de operatori liniari si marginiti,
supremumul realului spectrului este egal cu indicele de crestere
uniforma.Pentru aceasta, avem nevoie de urmatoarea teorema.
In cele ce urmeaza
presupunem ca X este un spatiu Banach complex.
Teorema 3. Daca
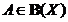 si
si 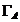 este o curba
simpla, inchisa si rectificabila care inconjoara
este o curba
simpla, inchisa si rectificabila care inconjoara 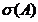 astfel incat pentru orice
astfel incat pentru orice 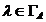 sa rezulte
sa rezulte 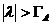 atunci
atunci
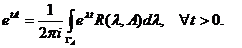
Demonstratie. Fie 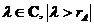 . Din
. Din
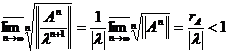
rezulta ca exista 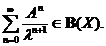 Un calcul simplu
arata ca
Un calcul simplu
arata ca
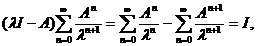
deci 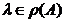 si
si
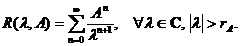 (1.10)
(1.10)
Pentru t > 0,
din (1.10) deducem ca
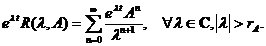
Fie 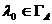 astfel incat
astfel incat 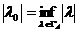 . Din
. Din
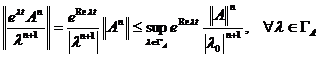
si faptul ca seria 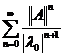 este convergenta
, rezulta ca seria
este convergenta
, rezulta ca seria 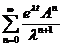 converge uniform in
raport cu
converge uniform in
raport cu 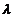 . Rezulta ca
. Rezulta ca
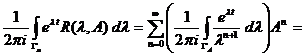
=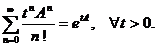
Teorema 4. Daca 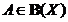 si
si 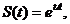 pentru orice t
pentru orice t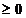 , atunci
, atunci
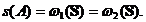
Demonstratie. Fie
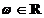 astfel incat
astfel incat 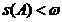 . Exista atunci o curba simpla, inchisa
si rectificabila
. Exista atunci o curba simpla, inchisa
si rectificabila 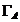 care inconjoara
care inconjoara 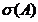 cu proprietatea
ca
cu proprietatea
ca 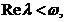 pentru orice
pentru orice 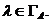 Notand cu
Notand cu 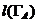 lungimea drumului
lungimea drumului 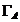 , din Teorema 1.3.3. rezulta ca
, din Teorema 1.3.3. rezulta ca
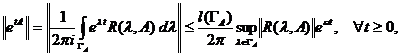
deci 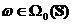 .
.
Obtinem astfel ca
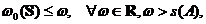
asadar, 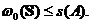 Tinand seama
de Corolarul 1.3.1. deducem ca
Tinand seama
de Corolarul 1.3.1. deducem ca
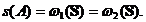
Remarca 6. In paragrafele urmatoare vom vedea
ca, in general, pentru semigrupuri cu generatori nemarginiti,
inegalitatile date de Corolarul 1. sunt stricte.


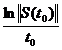 <
<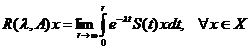 si
si 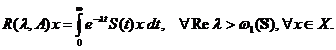
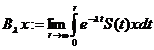
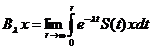 .
.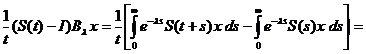
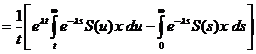 =
=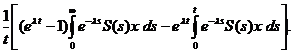
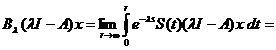
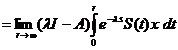 .
.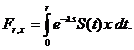
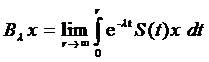 .
.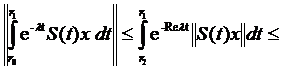
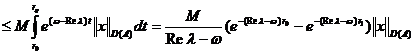
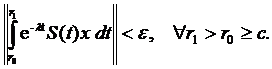
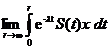 .
.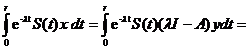
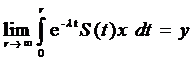 .
.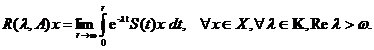
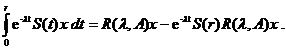
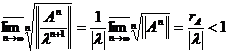
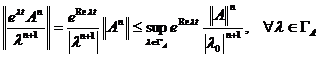
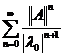 este convergenta
, rezulta ca seria
este convergenta
, rezulta ca seria