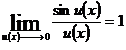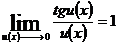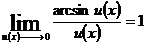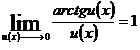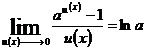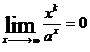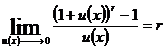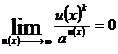INTEGRALA NEDEFINITA
1. Primitive. Proprietati.
Pe parcursul cursului, I este un interval;
Definitia
1 Fie f: I → R. Se spune ca f admite primitive pe I daca 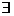 F : I →R astfel incat
F : I →R astfel incat
a) F este derivabila pe I;
b) F'(x) =f(x), 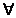 x I.
x I.
F
se numeste
primitiva lui f. ( I poate fi si o reuniune finita disjuncta de intervale
Demonstratie : Daca 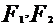 sunt primitive atunci
sunt primitive atunci 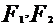 sunt derivabile
sunt derivabile 
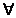 x ε I
x ε I
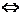
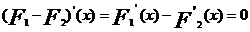 , x ε I.
, x ε I. 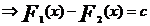 , c= constanta
, c= constanta
OBS 1. Fiind
data o primitiva 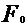 a unei functii atunci orice primitiva F a lui
f are forma F =
a unei functii atunci orice primitiva F a lui
f are forma F = 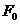 + c , c= constanta
+ c , c= constanta
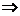 f admite o infinitate
de primitive.
f admite o infinitate
de primitive.
OBS 2. Teorema nu mai ramane
adevarata daca I este o reuniune disjuncta de intervale
Expl: f: R-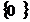 , f(x) = x²
, f(x) = x²
F = 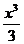 , G=
, G= 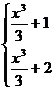 F, G sunt primitive ale lui f dar F-G
nu e constanta . Contradictie cu T 1.1
F, G sunt primitive ale lui f dar F-G
nu e constanta . Contradictie cu T 1.1
OBS 3. Orice functie care admite
primitive are Proprietatea lui Darboux.
Se stie ca derivata oricarei functii are P. lui
Darboux , rezulta ca f are P
lui Darboux. F' =f.
OBS 4. Daca I este interval si
f(I) 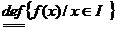 nu este interval atunci f nu admite primitive.
nu este interval atunci f nu admite primitive.
Daca presupunem ca f admite primitive atunci din OBS 3
rezulta ca f are P lui Darboux, rezulta f(I) este interval ceea
ce este o contradictie.
OBS 5. Orice functie continua
definita pe un interval admite
primitive.
Definitia
2 Fie f: I →R o functie care
admite primitive. Multimea tuturor primitivelor lui f se numeste integrala nedefinita a functiei f si se noteaza prin
simbolul 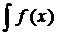 dx. Operatia de calculare a primitivelor unei
functii(care admite primitive ) se numeste integrare
dx. Operatia de calculare a primitivelor unei
functii(care admite primitive ) se numeste integrare
Simbolul 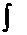 a fost propus pentru prima data de Leibniz, in
1675.
a fost propus pentru prima data de Leibniz, in
1675.
Fie F(I)= 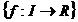 Pe aceasta
multime se introduc operatiile :
Pe aceasta
multime se introduc operatiile :
(f+g)(x) =f(x)+ g(x) ,
(αf)(x)=α.f(x)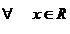 ,α constanta
,α constanta
C== 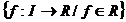
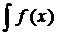 dx =
dx = .
.
Teorema 1.2 Daca
f,g:I→ R sunt functii care admit primitive si α 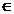 R, α ≠0,
atunci functiile f+g, αf admit de asemenea primitive si au loc
relatiile:∫(f+g) =∫f +∫g, ∫αf=α∫f,
α≠0, ∫f =∫f +C
R, α ≠0,
atunci functiile f+g, αf admit de asemenea primitive si au loc
relatiile:∫(f+g) =∫f +∫g, ∫αf=α∫f,
α≠0, ∫f =∫f +C
2.
PRIMITIVELE FUNCTIILOR CONTINUE SIMPLE
1. 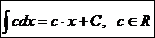 Ex
Ex 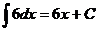
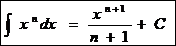 Ex
Ex 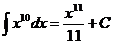
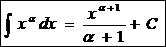 Ex
Ex 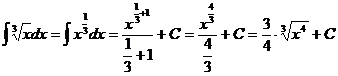
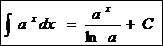 Ex
Ex 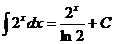
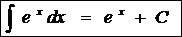 6.
6. 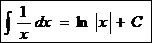 7.
7. 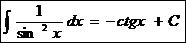
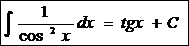 9.
9. 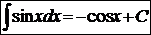 10.
10. 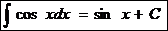
. 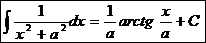 Ex
Ex 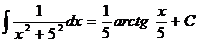
. 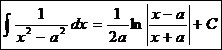 Ex
Ex 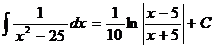
. 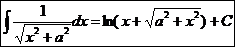 Ex
Ex 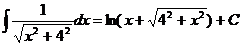
. 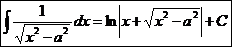 Ex
Ex 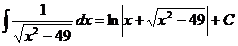
. 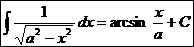 Ex
Ex 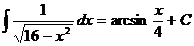
. 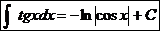 17.
17. 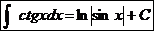
. 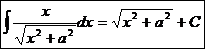 Ex
Ex 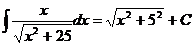
. 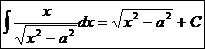 Ex
Ex 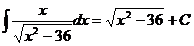
. 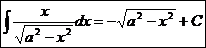 Ex
Ex 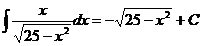
. 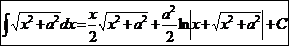 Ex
Ex 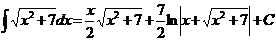
. 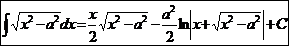 Ex
Ex 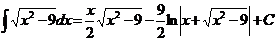
. 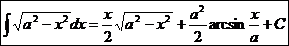 Ex
Ex 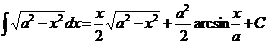
I. Sa se calculeze
primitivele urmatoarelor functii.
. ∫(3x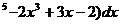 2. ∫ x(x-1)(x-2)dx
2. ∫ x(x-1)(x-2)dx
. ∫ 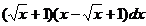 4. ∫
4. ∫ 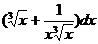
. 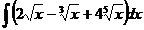 6.
6. 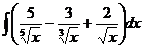
. ∫ x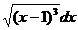 8.
8. 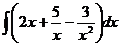
. ∫( e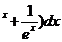 10. ∫ (x
10. ∫ (x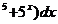
. 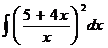 12.
12. 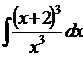
. ∫ 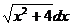 14. ∫
14. ∫ 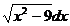
. ∫ 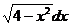 16*. ∫
16*. ∫ 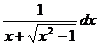
. 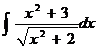 18*.
18*. 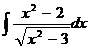
. 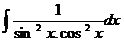 20*.
20*. 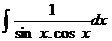
21*. 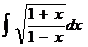

3.
PRIMITIVELE FUNCTIILOR CONTINUE COMPUSE
1. 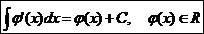 Ex
Ex 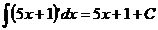
2. 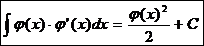 Ex
Ex 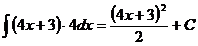
. 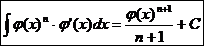 Ex
Ex
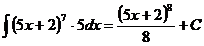
. 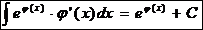 Ex
Ex 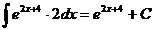
5. 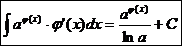 Ex
Ex
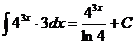
6.  Ex
Ex 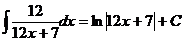
7. 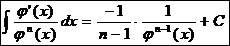 Ex
Ex 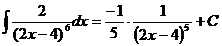
8. 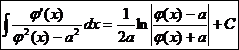 Ex
Ex 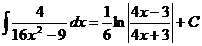
9. 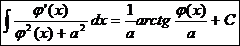 Ex
Ex 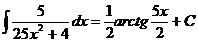
10. 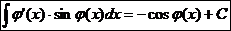 Ex
Ex 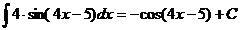
11. 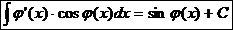 Ex
Ex 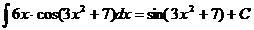
12. 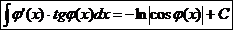 Ex
Ex
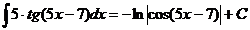
13. 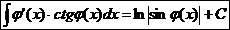 Ex
Ex
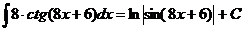
14. 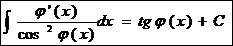 Ex
Ex 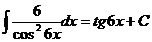
15. 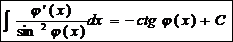 Ex
Ex 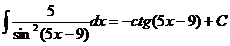
16. 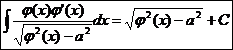 Ex
Ex 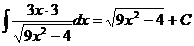
17. 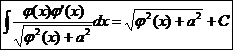 Ex
Ex 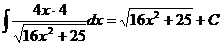
18. 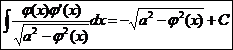 Ex
Ex 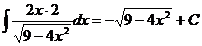
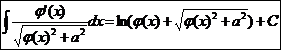 Ex
Ex 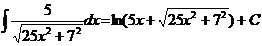
. 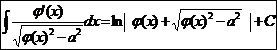 Ex
Ex 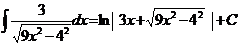
. 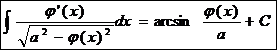 Ex
Ex 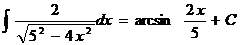
. 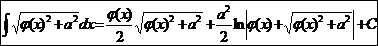
. 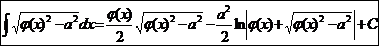
. 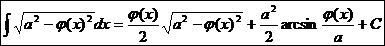
II.Sa se calculeze primitivele
urmatoarelor functii compuse.
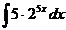 2.
2.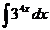 3.
3. 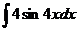 4.
4. 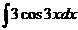
5. 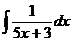 6.
6.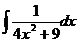 7.
7. 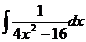 8.
8. 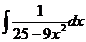
9.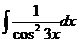 10.
10. 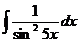 11.
11. 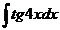 12.
12. 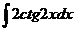
. 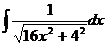 14.
14. 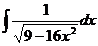
III. Sa se arate ca
urmatoarele functii nu admit primitive.
1. f: R → R, f(x) = 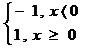 2. f: R → R , f(x) = [x] ( partea intreaga din x)
2. f: R → R , f(x) = [x] ( partea intreaga din x)
3. f: R → R, f(x) = 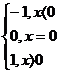 4. f: R → R , f(x) = [X] +X
4. f: R → R , f(x) = [X] +X
5. . f: R → R f(x) = 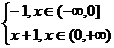 6. f: R → R , f(x) =
6. f: R → R , f(x) = 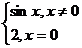
IV. Sa se determine a,b numere reale
astfel incat F sa fie primitiva unei functii f.
1*. F(x) = 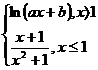 2*.
F(x) =
2*.
F(x) = 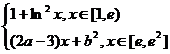
3*. F(x) = 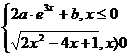 4*. F(x) =
4*. F(x) =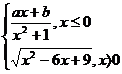
5*. F(x) = 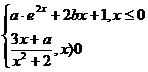 6*. F(x) =
6*. F(x) =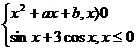
V. Sa se verifice daca
urmatoarele functii admit primitive si in caz afirmativ sa
se determine o primitiva.
1. f: R→ R, f(x) = 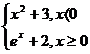 2.
f: R→ R, f (x) =
2.
f: R→ R, f (x) = 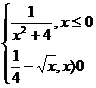
3*.f:[0,∞)→R,
f(x) = 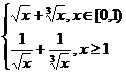 4*. f:[-2,∞)→R, f(x) =
4*. f:[-2,∞)→R, f(x) = 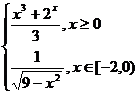
DERIVATE
|
Nr
|
FUNCTIA
|
DERIVATA
|
MULTIMEA
PE CARE FUNCTIA ESTE DERIVABILA
|
FUNCTIA
COMPUSA
|
Derivata
|
|
C
|
|
R
|
|
|
|
x
|
|
R
|
u
|
u'
|
|
xn
|
nxn-1
|
R
|
un
|
n.un-1.u'
|
|
xa
|
axa-1
|
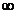
|
ua
|
aua-1.u'
|
|

|
-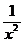
|
R*
|
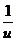
|
-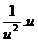 ' '
|
|
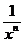
|
-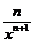
|
R*
|
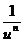
|
-n/un+1·u'
|
|
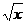
|
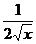
|
R*+
|
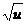
|
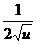 u' u'
|
|
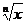
|
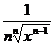
|
R*+,n par
R*,n impar
|
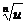
|
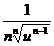 u' u'
|
|
sin x
|
cosx
|
R
|
sin
u
|
u'cos
u
|
|
cos x
|
-sinx
|
R
|
cos u
|
-u'sin u
|
|
tg x
|
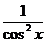
|
R
|
tg u
|
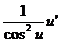
|
|
ctg x
|
-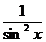
|
R
|
ctg
u
|
-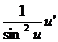
|
|
arcsin x
|
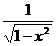
|
|
arcsin
u
|
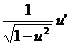
|
|
arccos x
|
-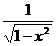
|
|
arccos
u
|
-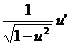
|
|
arctg x
|
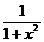
|
R
|
arctg
u
|
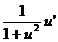
|
|
arcctg x
|
-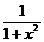
|
R
|
arcctg
u
|
-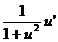
|
|
ax
|
a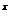 lna lna
|
R
|
au
|
au.lna.u'
|
|
ex
|
e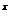
|
R
|
eu
|
eu.u'
|
|
lnx
|
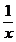
|
R*+
|
lnu
|
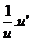
|
|
log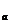 x x
|
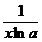
|
R*+
|
logau
|
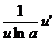
|
|
uv
|
(uv)' = v. uv-1.u' + uv.v'.lnu
|
LIMITE DE FUNCTII
P(X)=a0xn
+ a1xn-1 + . . . . . ..+an ,a0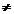 0 Q(X)=b0xm
+ b1xm-1 + . . . . . ..+bn ,b0
0 Q(X)=b0xm
+ b1xm-1 + . . . . . ..+bn ,b0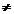 0
0
|
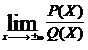
=
|
|
|
|
|
|
n<m
|
|
|
|
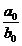
|
|
|
n=m
|
|
|
x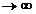
|
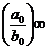
|

|
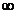 , ,
|
n>m,
|
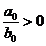
|
|
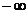 , ,
|
n>m,
|
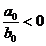
|
|
x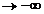
|
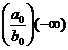 n-m n-m
|

|
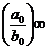
|
n>m,
|
n-m par
|
|
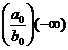
|
n>m,
|
n-m impar
|
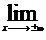
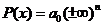
|
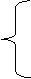
|
|
|
daca
|
q
|
|
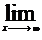 qx = qx =
|
|
|
daca
|
q=1
|
|
|
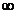 , ,
|
daca
|
q>1
|
|
|
nu
exista,
|
daca
|
q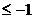
|


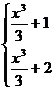
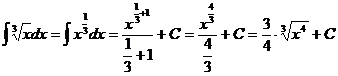
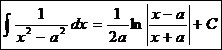
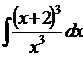
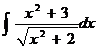
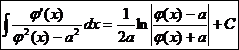 Ex
Ex 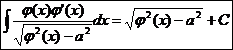 Ex
Ex 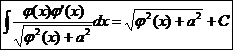 Ex
Ex  Ex
Ex 
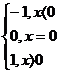 4. f: R → R , f(x) = [X] +X
4. f: R → R , f(x) = [X] +X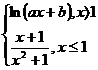
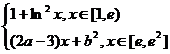
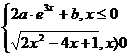 4*. F(x) =
4*. F(x) =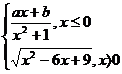
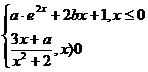 6*. F(x) =
6*. F(x) =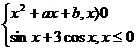
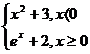 2.
f: R→ R, f (x) =
2.
f: R→ R, f (x) = 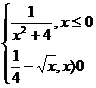
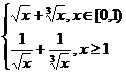
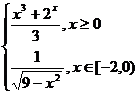
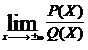
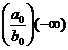 n-m
n-m