Definita unei categorii. Exemple
Definitia
1.1: O categorie 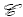 este data de o clasa C de obiecte si o clasa C de morfisme, care au urmatoarea structura
este data de o clasa C de obiecte si o clasa C de morfisme, care au urmatoarea structura
Fiecare morfism are un domeniu si
un codomeniu, care sunt obiecte. Scriem:
f :X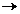 Y sau X
Y sau X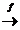 Y
Y
daca X este domeniul
morfismului f si Y este codomeniul morfismelor.
Mai putem scrie : X dom( f) si Y cod ( f);
(X, Y) reprezinta clasa
morfismelor de la X la Y. (sau, inca, Hom (X, Y) )
Fiind date doua
morfisme f si g astfel incat cod ( f ) = dom (
f ) , compunerea lui f si g , notata go f, este definita si are domeniul dom(
f) si codomeniul cod (g) .
X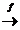 Y
Y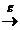 Z
Z
Compunerea morfismelor este asociativa,
adica: fiind date morfismele:
f :X 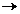 Y, g:Y
Y, g:Y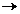 Z, h:Z
Z, h:Z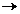 W
W
h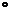 (g
(g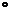 f)
f) 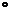 (h
(h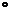 g)
g) 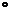 f;
f;
Pentru fiecare
obiect X , exista morfismul identitate , notat cu id X, astfel incat:
idX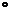 g=g, oricare ar fi g:Y
g=g, oricare ar fi g:Y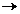 X
X
si
f 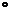 idx =f, oricare ar fi f: X
idx =f, oricare ar fi f: X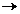 Y.
Y.
Exemple de
categorii:
1
este categoria cu un obiect * si un morfism id
0
este categoria vida.
Orice multime preordonata
este o categorie
O preordine (multime
preordonata) este o multime X impreuna cu o
relatie binara "
", reflexiva si tranzitiva.
reflexivitatea: rezulta din
existenta lui idX
tranzitivitatea: rezulta din compunerea morfismelor.
Preordinea poate fi
vazuta ca o categorie, cu C = X si C
Set este categoria tuturor multimilor, avand ca
obiecte, multimile, iar ca morfisme, functiile dintre multimi.
Rel este categoria avand drept obiecte,
multimile, iar ca morfisme, relatiile dintre multimi.
Multe
categorii de baza au ca obiecte anumite structuri matematice, iar ca
morfisme functiile ce
pastreaza structura.
Obs: Nu toate grafurile sunt categorii, pentru
ca compunerea a doua arce nu este intotdeauna un arc.
Sgr este
categoria semigrupurilor, avand ca obiecte semigrupurile, iar ca morfisme, morfismele de semigrupuri.
Mon este categoria monoizilor, avand ca obiecte
monoizii, iar ca morfisme, morfismele (unitare) de monoizi (care transfera
si elementul neutru).
d)
Gr este categoria grupurilor, avand ca obiecte
grupurile, iar ca morfisme morfismele dintre grupuri.
Ab este categoria grupurilor abeliene,
avand ca obiecte grupurile abeliene, iar ca morfisme morfismele de grupuri abeliene.
Ring este categoria inelelor, avand ca obiecte
inelele, iar ca morfisme morfismele de inele.
e)
Top este categoria spatiilor topologice, avand
ca obiecte spatiile topologice, iar ca morfisme functiile continue.
Pos este categoria multimilor partial
ordonate si a functiilor monotone.
Categoria
morfismelor unei categorii C, notata C,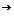
Obiectele sunt
perechile de forma (X,
f,Y), unde X, Y 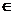 C si f
C si f 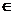 C . Un morfism de la (X, f,Y)
la (X' ,
f' ,Y' ) este o pereche de C - morfisme (hX, hY ) cu
C . Un morfism de la (X, f,Y)
la (X' ,
f' ,Y' ) este o pereche de C - morfisme (hX, hY ) cu
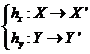
astfel incat hY 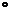 f=f'
f=f' 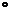 hX
hX
11) Categoria duala
unei categorii C notata C,  care se
obtine prin procedeul de
care se
obtine prin procedeul de
"intoarcere a sagetilor".
Obiectele sunt obiectele categoriei C iar ca morfisme, daca
X, Y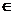 C , atunci C
C , atunci C 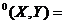 C
C 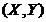
Graph este categoria grafurilor, avand ca
obiecte grafurile, iar ca morfisme morfismele de grafuri. Sa reamintim
constructia lor:
Un graf G este un 4-uplu G = (G , G , s, t), unde G este multimea nodurilor sau varfurilor, G este multimea muchiilor sau arcelor,
s, t : E V, care "ofera" sursa, respectiv tinta fiecarei muchii. Un morfism de
grafuri (avand in vedere ca fiecare graf are in definitia sa cate doua multimi)
va fi atunci o pereche de functii care sa pastreze structura. Avand doua grafuri, G = (G , G , s,
t) si G' = (G' , G' , s', t'),
un morfism de la G la G' ,
notat (φ ):G
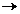 G' , este o pereche de functii φ : G
G' , este o pereche de functii φ : G 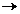 G' : G
G' : G 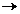 G' astfel
G' astfel
incat urmatoarele diagrame sunt comutative in Set
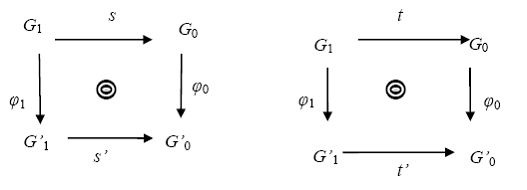
13) Drumuri
intr-un graf Dat un graf G G G s t),
se numeste drum de lungime k
de la
a 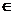 G la b
G la b 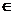 G , un sir de k arce f , f , , fk astfel incat:
G , un sir de k arce f , f , , fk astfel incat:
s(f ) = a, t(fk) = b
t(fi ) = s(fi
Vom nota un astfel de drum prin (f , f , , fk
Conventie:
exista un drum de lungime 0, unic pentru fiecare nod.
Doua arce f si g se
numesc compozabile daca t(f)
= s(g). Vom nota G multimea lor, iar prin f
; g, drumul obtinut prin compunerea lor.
Aceasta definitie se extinde, in mod
natural, si la drumuri de lungime oarecare.
In acest
mod obtinem o noua categorie, Pa(G), avand drept
obiecte nodurile grafului si drept morfisme
drumurile din graf.
Tipuri. Tipurile sunt utilizate pentru
clasificarea "lucrurilor". Conform cu prima dogma a lui Goguen, ele ar trebui sa formeze o
categorie avand tipurile drept obiecte (clar, pot aparea mai multe categorii, dupa modul de
clasificare).
Un exemplu simplu sunt tipurile "produs
finit", care sunt reprezentate prin numere naturale, iar morfismele prin ceea ce s-ar numi "operatii
de transfer de registri". Sa detaliem:
Astfel, n N indica un n-uplu t , t , ,
tn de itemi de
date in n "registri". Un morfism f : m 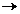 n este
o functie care indica
faptul ca, continutul registrului
f(i) ar trebui transferat
registrului i, i= 1,..,n. In fapt, noi identificam
numarul n cu multimea (si 0 cu
n este
o functie care indica
faptul ca, continutul registrului
f(i) ar trebui transferat
registrului i, i= 1,..,n. In fapt, noi identificam
numarul n cu multimea (si 0 cu 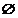 ), aceasta categorie devenind opusa unei
subcategorii a lui Set. Sa o notam cu N
), aceasta categorie devenind opusa unei
subcategorii a lui Set. Sa o notam cu N
Limbajele
de programare functionale, din punct de vedere categorial.
Un limbaj de
programare functional se poate descrie, in mare, ca fiind un limbaj care
da utilizatorului
cateva tipuri, operatii primitive si constructori, de la care
pornind, se obtin tipuri
si operatii mai complicate. Scrierea unui program in aceste limbaje
inseamna, in fond, aplicarea
acestor constructori tipurilor, constantelor si functiilor. "Rularea"
unui program este
constituita din aplicarea unui astfel de operator constantelor de intrare
pentru obtinerea unor valori. Avem asadar:
FPL-1:
tipuri de date primitive, date in limbaj
FPL-2:
constante de fiecare tip
FPL-3:
operatii = functii intre tipuri
FPL-4:
constructori - se aplica tipurilor de date si operatiilor pentru
a produce tipuri de date si operatii derivate
Limbajul = multimea tuturor operatiilor si tipurilor derivate din
operatiile si tipurile de date primitive.
 Daca vom face 3 presupuneri
suplimentare, vom putea privi in mod direct cum unui limbaj functional L ii corespunde, in mod canonic, o
categorie
Daca vom face 3 presupuneri
suplimentare, vom putea privi in mod direct cum unui limbaj functional L ii corespunde, in mod canonic, o
categorie 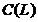
A-1 Presupunem ca exista o operatie
"do-nothing" , idA, pentru fiecare tip A. Cand se
aplica, ea nu face nimic tipului de date respectiv.
A-2 Adaugam limbajului un tip
aditional, numit 1, care are proprietatea ca din fiecare tip A exista o
unica operatie la 1. Interpretam fiecare constanta
c de tip A ca fiind
o sageata c : 1 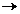 A. In
acest fel, constantele sunt incorporate multimii operatiilor.
A. In
acest fel, constantele sunt incorporate multimii operatiilor.
A-3 Presupunem ca limbajul are un constructor
de compunere: pentru o operatie f care ia ca intrare ceva de tip A s
produce ceva de tip B, si o alta operatie g avand drept input ceva de tip B si
produce un output de tip C, avem operatia derivata f ; g,
care are input din A si output din C.
In acest fel, putem organiza limbajul ca si categorie pentru care:
FPC-1: tipurile sunt obiectele categoriei
FPC-2 : Operatiile (derivate si primitive) sunt morfismele
categoriei
FPC-3
: sursa si tinta unui morfism sunt tipul de intrare si tipul de
iesire a operatiei respective
FPC-4:
Compunerea morfismelor este data de constructorul de compunere
FPC-5:
Morfismele identitate sunt operatiile "do-nothing" asociate fiecarui
tip
Sa vedem si un exemplu concret:
Avem un limbaj cu 3 tipuri de date NAT, BOOLEAN, si CHAR.Vom da o descriere a operatiilor in stil
categorial:
NAT are o constanta NAT si o
operatie s u c c
: NAT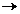 NAT
NAT
2 constante true
si f a l s
e : 1 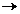 BOOLEAN si o operatie care satisface true;
= false si false;
= true
BOOLEAN si o operatie care satisface true;
= false si false;
= true
CHAR
are cate o constanta c : 1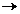 CHAR pentru fiecare
caracter.
CHAR pentru fiecare
caracter.
operatii
de conversie de tip ord :
CHAR 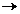 NAT, chr :
NAT
NAT, chr :
NAT 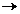 CHAR. Ele
CHAR. Ele
satisfac
ecuatiile ord ; chr = idCHAR
Obiectele categoriei sunt NAT, BOOLEAN,
CHAR si 1. Morfismele categoriei sunt
programele scrise in acest limbaj. De exemplu, morfismul
next : CHAR 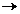 CHAR
CHAR
(programul care ne ofera urmatorul
caracter) este obtinut ca o compunere:
next = ord ; succ ; chr
Observatie:
Orice categorie poate fi privita, intr-un sens generalizat, ca un graf.
Acest graf are obiectele drept noduri iar arcele sunt morfismele dintre
obiecte. Odata ce am facut
aceasta legatura, pentru o categorie C sa notam prin graph() graful
asociat categoriei.
Definitie Fie I un graf si
C
o categorie. Se numeste diagrama in C de forma I, un morfism de
grafuri
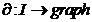 ( C ) . O diagrama se numeste a fi comutativa
daca pentru orice doua noduri x, y si orice doua drumuri (f , f , , fk), (g , g , , gm de la x la y in graful I, avem
( C ) . O diagrama se numeste a fi comutativa
daca pentru orice doua noduri x, y si orice doua drumuri (f , f , , fk), (g , g , , gm de la x la y in graful I, avem
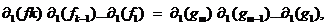
in C .
Observatie Faptul ca o diagrama este
comutativa stabileste o serie de egalitati intre arce. In
acest fel obtinem o
posibilitate de a face rationamente ecuationale in forma "vizuala",
avantaj care nu a fost inca
exploatat in ingineria software.
Definitii (tipuri de obiecte):
Un obiect X dintr-o categorie se numeste final (terminal)
daca pentru oricare alt obiect Y
exista exact un singur morfism Y X in categorie.
Dual,
X este initial daca pentru toate obiectele Y
exista un singur morfism X Y
Fie C
o categorie
Definitia 1.4: Fie
D este o subcategorie
a lui C
daca
i)
D 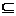 C
C
ii) (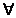 )A, B
)A, B 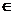 D D(A,
B)
D D(A,
B)
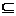 C(A,
B) ;
C(A,
B) ;
iii) Compunerea
morfismelor in D este acceasi ca in C
iv) (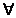 )A
)A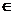 D : idA in D este acelasi cu idA in C(A,
B) .
D : idA in D este acelasi cu idA in C(A,
B) .
In plus, daca (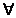 )A, B
)A, B 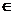 D D (A, B)=C (A, B) , atunci D se numeste subcategorie plina a lui C
D D (A, B)=C (A, B) , atunci D se numeste subcategorie plina a lui C
Exemple
a)
Ab este subcategorie plina a lui Gr.
b)
Gr este subcategorie plina a lui Sgr.
c)
Sgr este subcategorie a lui Set care nu
este plina.
d)
Mon este subcategorie a lui Sgr care nu
este plina.
Dualitate
in teoria categoriilor
Fie P un enunt care se exprima in termeni de categorie,
morfism si obiecte. Exprimand acest enunt pentru
o categorie C si pentru C
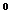 se
obtin doua enunturi P(C) si P(C
o ). Daca in enuntul P(C
se
obtin doua enunturi P(C) si P(C
o ). Daca in enuntul P(C 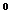 )
obiectele si morfismele sunt privite
si interpretate ca obiecte si morfisme ale categoriei C atunci se obtine un nou enunt P
)
obiectele si morfismele sunt privite
si interpretate ca obiecte si morfisme ale categoriei C atunci se obtine un nou enunt P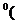 C
C
P C
) si P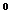 (C ) se numesc enunturi duale.
(C ) se numesc enunturi duale.
P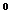 (C ) se
obtine din P(C
) "intorcand sagetile".
(C ) se
obtine din P(C
) "intorcand sagetile".
Teorema (Principiul de dualitate in teoria categoriilor)
Fie P un enunt care se
exprima in termeni de categorie, morfism si obiecte. Daca P
este adevarat pentru orice categorie C atunci si dualul acestuia este adevarat pentru orice
categorie.
Morfisme si obiecte remarcabile intr-o categorie
Fie C o categorie si f 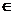 C (A, B) morfism de la A
la B.
C (A, B) morfism de la A
la B.
Definitii 1.5 (morfisme):
Spunem ca f este mono (sau monomorfism,
sau monomorfic) daca pentru ( )C C (obiect
in C ) si ( ) u,
v C (C, A) f o u = f o v T u= v.
Spunem ca f este epi (sau epimorfism,
sau epimorfic) daca pentru ( )
C C (obiect in ) si
)u,v C (B,C) uo f =vo
f Tu=v.
Un
morfism care este si mono si epi se numeste bimorfism.
Functia f se numeste izomorfism daca este inversabil la stanga si la dreapta adica:
)g (B,
A) astfel incat
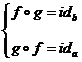 unde g se numeste
inversa lui f si, daca exista este unica
unde g se numeste
inversa lui f si, daca exista este unica
Notam: 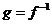
Observatii:
Definitia epimorfismelor este
duala monomorfismelor. Adica, f este epi in C daca si numai daca f este mono in se numeste inversa lui f si, daca
exista, C  si invers.
si invers.
In Set, f este mono daca si numai daca
f este o functie injectiva. Este valabil si in Grp, Graph,
Rng, Preord, Pos,
In Set, f este epi
daca si numai daca f este o functie surjectiva.
Este valabil si pentru Grp, dar nu pentru Mon.
In general, doua obiecte izomorfe
sunt tratate ca fiind "in esenta" aceleasi.
Proprietatea obiectelor de a fi izomorfe
trebuie vazuta in contextul "vietii sociale" care este data de categoria in discutie.
Avand o alta categorie, cu aceleasi obiecte, dar referitoare la alte aspecte structurale, doua
obiecte pot fi izomorfe in prima categorie fara a fi izomorfe in cea de a doua.
Un exemplu in sensul mentionat
anterior apare in dezvoltarea software-ului orientat-obiect: doua obiecte pot fi considerate
izomorfe ca avand aceeasi interfata si aratand acelasi
comportament al interfetelor lor. Pe de alta parte aeste obiecte pot
avea implementari complet
diferite.
Vom incheia acest prim paragraf prin studiul unui
alt exemplu de categorie provenind din informatica, si anume categoria automatelor.
Exista mai multe variante de automate si
ne vom opri pentru moment la automatele Moore: Definitie 1.6 Un automat Moore este un 5-uplu A = (X, S,Y,
s
, f, g) unde:
X, o multime nevida, numita alfabet
de intrare,
Y alfabetul de iesire,
S este multimea starilor, s este starea initiala, s S
f: X S S functia de tranzitie,
g : S → Y este functia de intrare.
Faptul ca f (a, s ) = s si g ( s ) = b se interpreteaza
astfel:
Automatul este in starea s si primeste intrarea a,
si atunci trece in starea s , eliberand b.
Notiunea de morfism de automate
trebuie sa aiba posibilitatea de a "captura" structura unui automat, indicand modul in care automatul
poate fi simulat de un altul. Cu alte cuvinte, un morfism trebuie sa transleze multimile de
intrare, de stari, de iesire in asa fel incat functiile de
tranzitie, starile
de intrare si functiile de iesire "sa se corespunda".
In acest fel ajungem la urmatoarea
definitie pentru morfisme de automate:
Definitie
1.7
Date doua automate A = (X, S,Y, s , .f, g) si A' =
(X', S',Y', s' , .f', g'), se numeste morfism de automate, notat  : A →
A', un triplet
: A →
A', un triplet  = (h, i,
j), unde h : X →
X', i : S
→ S' si j : Y → Y' astfel incat sa fie
indeplinite conditiile:
= (h, i,
j), unde h : X →
X', i : S
→ S' si j : Y → Y' astfel incat sa fie
indeplinite conditiile:
i(s ) = s'
i ◦ f = f' ◦ (hืi)
j ◦ g = i ◦ g'
Aceste conditii pot parea, la prima
vedere, destul de greu de retinut. Daca, insa, vom utiliza diagramele pentru reprezentarea
vizuala a acestor ecuatii, totul devine simplu:
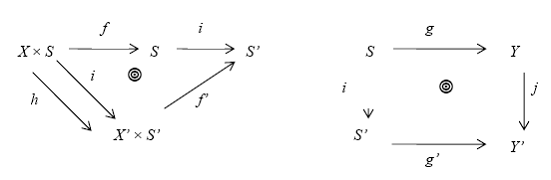
Fie A un automat. Este clar ca
nu orice stare din automat este interesanta ci numai acelea pentru care
exista o posibilitate de a ajunge pornind din starea initiala
(sau, inca, cele pentru care exista un drum in graful de tranzitie
asociat, pornind din starea initiala). Astfel de stari se numesc
stari accesibile. Un automat pentru care toate starile sunt
accesibile se numeste automat accesibil (reachable automaton).
Starile inaccesibile pot fi
eliminate, pastrandu-se numai starile accesibile. Vom obtine in acest mod un nou automat, AR asociat lui A.
Considerand numai automatele accesibile,
obtinem o noua categorie, categoria automatelor accesibile, pe care o vom nota cu REACH. Este evident
ca REACH este o subcategorie plina a lui AUTOM
Ideea este ca, in scopul simularii
altor automate, orice automat poate fi reprezentat prin automatul accesibil asociat se poate formula in
modul urmator:
Fie A = (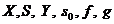 ) si A = (
) si A = (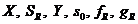 ) automatul accesibil asociat.
) automatul accesibil asociat.
Avem un morfism canonic asociat,  ,
, 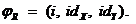
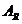 si
si 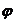 satisfac urmatoarea proprietate:
satisfac urmatoarea proprietate:
"Pentru orice R un automat accesibil
si orice simulare 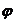 : R → A, exista un unic
morfism in REACH
: R → A, exista un unic
morfism in REACH 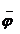 : R →
: R → 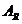 astfel incat
astfel incat 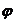
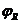 ◦
◦ 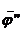 . Astfel, urmatoarea diagrama
este commutativa:
. Astfel, urmatoarea diagrama
este commutativa:
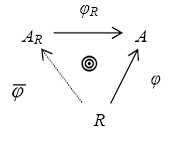



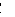 Cu alte cuvinte,
Cu alte cuvinte, 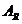 este cel
mai "apropiat" automat accesibil de A adica orice alt automat
accesibil care poate fi simulat de A poate fi simulat de
este cel
mai "apropiat" automat accesibil de A adica orice alt automat
accesibil care poate fi simulat de A poate fi simulat de 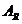


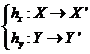

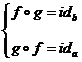 unde g se numeste
inversa lui f si, daca exista este unica
unde g se numeste
inversa lui f si, daca exista este unica 


