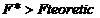Execitiu - Teste asupra coeficientilor si variantei
erorilor
Despre o firma, se cunosc
datele referitoare la vanzarile de marfa, y, exprimate in mii euro, pe o perioada de 14 luni,
numarul de angajati (persoane), x1,
cheltuielile de intretinere a utilajelor, exprimate in euro, x2, si cheltuielile de
publicitate pentru promovarea produselor, exprimate in euro, x3. Datele sunt prezentate in
Tabelul 2.4:
Tabelul
2.4. Datele referitoare la un agent economic
Se cere:
a) Sunt
semnificative variabilele exogene in explicarea variatiei variabilei
endogene
Sa se argumenteze si prin calculul intervalelor de incredere ale
estimatorilor coeficientilor.
b) Coeficientul a1 este semnificativ mai mic
decat 1
c)
Coeficientii a1
si a2 sunt
semnificativi si simultan diferiti de 1, respectiv -0.5?
d) Care este
intervalul de incredere pentru varianta erorii pentru un prag de
semnificatie a
Solutie:
In
Figurile 2.16, 2.17, si 2.18 sunt prezentate corelatiile dintre
variabila dependenta, stabilita ca fiind vanzarile de
marfa, influentata de celelalte variabile, considerate factori.
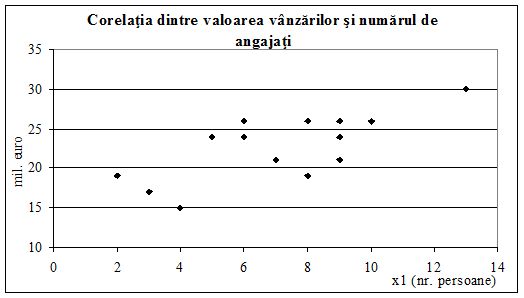
Figura
2.16. Legatura directa dintre valoarea vanzarilor si
numarul de angajati
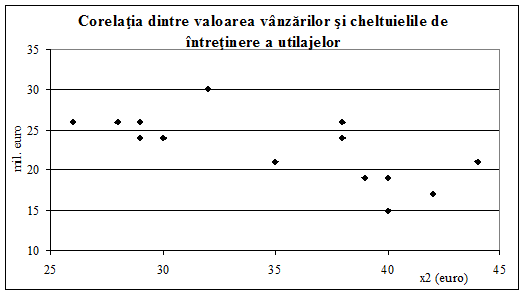
Figura
2.17. Legatura inversa dintre valoarea vanzarilor si
cheltuielile cu utilajele
Se
observa in cele trei grafice legaturile de natura directa
ale vaorii vanzarilor cu numarul de angajati si
cheltuielile de publicitate si de sens invers cu cheltuielile de
intretinere a utilajelor. Cu cat sunt mai mari aceste cheltuieli de
intretinere, cu atat se reduc vanzarile din cauza stagnarilor in
productie pentru repararea utilajelor, cresterii costurilor de
fabricatie si implicit a preturilor de vanzare a produselor,
reducerii altor cheltuieli, cum ar fi cele de aprovizionare cu materii prime
si materiale, salariile personalului angajat, etc.
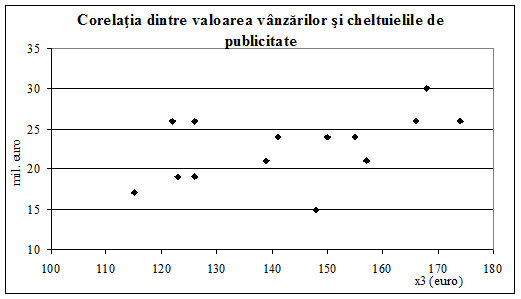
Figura
2.18. Legatura directa dintre valoarea vanzarilor si
cheltuielile de publicitate
In
urma analizei de regresie, se asteapta un coeficient negativ pentru
variabila explicativa a cheltuielilor de intretinere a utilajelor, x2 si coeficienti
pozitivi pentru celelalte doua variabile independente x1 si x3.
Tabela de regresie este
prezentata in Tabelul 2.5:
|
SUMMARY OUTPUT
|
|
|
|
|
|
|
Regression Statistics
|
|
|
|
|
|
|
Multiple R
|
|
|
|
|
|
|
|
R Square
|
|
|
|
|
|
|
|
Adjusted R Square
|
|
|
|
|
|
|
|
Standard Error
|
|
|
|
|
|
|
|
Observations
|
|
|
|
|
|
|
|
ANOVA
|
df
|
SS
|
MS
|
F
|
Significance F
|
|
|
Regression
|
|
|
|
|
|
|
|
Residual
|
|
|
|
|
|
|
|
Total
|
|
|
|
|
|
|
|
Coefficients
|
Standard Error
|
t Stat
|
P-value
|
Lower 95%
|
Upper 95%
|
|
Intercept
|
|
|
|
|
|
|
|
X Variable 1
|
|
|
|
|
|
|
|
X Variable 2
|
|
|
|
|
|
|
|
X Variable 3
|
|
|
|
|
|
|
Tabelul
2.5. Tabela de regresie a modelului cu trei variabile explicative
Modelul este 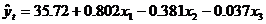 , iar valorile teoretice, yt1,
se afla in Tabelul 2.4 si pe acelasi grafic care arata
evolutia in timp a valorilor observate, in Figura 2.19.
, iar valorile teoretice, yt1,
se afla in Tabelul 2.4 si pe acelasi grafic care arata
evolutia in timp a valorilor observate, in Figura 2.19.
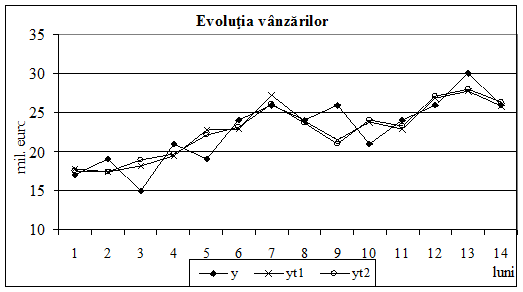
Figura
2.19. Evolutia vanzarilor si ajustarea lor
a) Ratia
Student pentru fiecare coeficient de regresie, calculata dupa formula
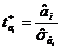 , se compara cu valoarea teoretica Student pentru a=5% si 10 grade de libertate,
, se compara cu valoarea teoretica Student pentru a=5% si 10 grade de libertate, 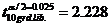 .
.
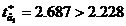 , rezulta ca
, rezulta ca 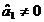 , variabila x1
contribuie la explicarea variatiei variabilei y;
, variabila x1
contribuie la explicarea variatiei variabilei y;
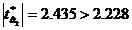 , rezulta ca
, rezulta ca 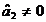 , variabila x2
contribuie la explicarea variatiei variabilei y;
, variabila x2
contribuie la explicarea variatiei variabilei y;
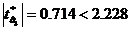 , rezulta ca
, rezulta ca 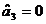 , variabila x3
nu contribuie la explicarea
variatiei variabilei y, si
poate fi retrasa din model. Se poate vedea in tabele de regresie din
Tabelul 2.5 ca P-value pentru
estimatorul
, variabila x3
nu contribuie la explicarea
variatiei variabilei y, si
poate fi retrasa din model. Se poate vedea in tabele de regresie din
Tabelul 2.5 ca P-value pentru
estimatorul 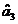 , indica un prag de semnificatie de 49%, care este
mult prea mare.
, indica un prag de semnificatie de 49%, care este
mult prea mare.
Intervalul de incredere al
coeficientului ai se
stabileste in functie de valoarea estimatorului, estimatia abaterii
sale si valoarea teoretica Student pentru un prag de
semnificatie ales, de obicei a=5%: 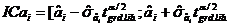 .
.
Intervalele de
incredere pentru cei trei estimatori ai coeficientilor variabilelor
explicative sunt:
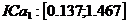 , semnul "+" indica legatura directa dintre y si x1;
, semnul "+" indica legatura directa dintre y si x1;
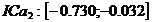 , semnul "-" indica legatura inversa dintre y si x2 (Figura 2.17);
, semnul "-" indica legatura inversa dintre y si x2 (Figura 2.17);
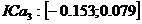 , se schimba semnul de la "-" la "+",
, se schimba semnul de la "-" la "+", 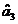 poate lua valoarea 0,
nu este semnificativ diferit de 0. Numai variabilele x1 si x2
sunt variabile exogene semnificative.
poate lua valoarea 0,
nu este semnificativ diferit de 0. Numai variabilele x1 si x2
sunt variabile exogene semnificative.
Pentru noul model cu doua
variabile explicative, se obtine tabela de regresie prezentata in
Tabelul 2.6. Valorile teoretice calculate cu acest model: 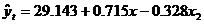 se afa in Tabelul
2.4 si pe graficul din Figura 2.19.
se afa in Tabelul
2.4 si pe graficul din Figura 2.19.
Se poate observa ca acest model
are coeficientii semnificativ diferiti de 0, dupa cum
indica ratiile Student calculate, care sunt mai mari decat valoarea
teoretica din tabela Student, valorile P-value,
care sunt mai mici decat 5%, precum si intervalele de incredere ale
coeficientilor, care nu schimba semnul de la limita inferioara
la cea superioara, deci nu contin valoarea 0.
Intervalele de
incredere sunt: 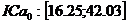 ,
, 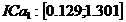 ,
, 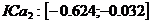 .
.
Coeficientul de
determinatie de 68.7% indica validitatea modelului liniar, iar
coeficientul de corelatie multipla de 0.83 indica o
corelatie puternica intre cele trei variabile y, x1 si x2.
|
SUMMARY OUTPUT
|
|
|
|
|
|
|
Regression Statistics
|
|
|
|
|
|
|
Multiple R
|
|
|
|
|
|
|
|
R Square
|
|
|
|
|
|
|
|
Adjusted R Square
|
|
|
|
|
|
|
|
Standard Error
|
|
|
|
|
|
|
|
Observations
|
|
|
|
|
|
|
|
ANOVA
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Significance F
|
|
|
Regression
|
|
|
|
|
|
|
|
Residual
|
|
|
|
|
|
|
|
Total
|
|
|
|
|
|
|
|
Coefficients
|
Standard Error
|
t Stat
|
P-value
|
Lower 95%
|
Upper 95%
|
|
Intercept
|
|
|
|
|
|
|
|
X Variable 1
|
|
|
|
|
|
|
|
X Variable 2
|
|
|
|
|
|
|
Tabelul
2.6. Tabela de regresie a modelului cu doua variabile explicative
b) Intrebarile
b), c) si d) ale exercitiului, se refera la modelul
initial, cel cu trei variabile explicative, a carui tabela de regresie
se afla in Tabelul 2.5.
Pentru
a testa valoarea coeficientului a1
daca este semnificativ diferita de 1, ipotezele testului sunt:
H0: a1=1
H1: a1<1
Testul
este unilateral la stanga, iar valoarea teoretica Student pentru 10 grade
de libertate si a=5%, este 1.81. Presupunand
adevarata ipoteza nula, raportul critic sau ratia Student
calculata, devine: 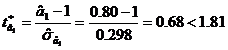 . Se accepa ipoteza nula, coeficientul a1 nu este semnificativ
inferior valorii 1.
. Se accepa ipoteza nula, coeficientul a1 nu este semnificativ
inferior valorii 1.
2.6.3. Analiza variantei - testul Fisher de semnificatie
globala a regresiei
Tabelul
de analiza a variantei, ANOVA este de forma celui din Tabelul 2.7:
|
Natura variatiei, datorata:
|
Suma
de patrate (Sum of Squares) SS
|
Grade de libertate
(degrees
freedom) df
|
(Modified Sums) MS
|
Testul
Fisher F
|
|
Regresiei (variabilelor explicative)
|
SSE=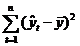
|
k
|
SSE/k
|
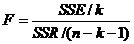
|
|
Reziduurilor (varianta
neexplicata)
|
SSR=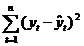
|
n-k-1
|
SSR/(n-k-1)
|
|
Totala (toti factorii)
|
SST=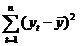
|
n-1
|
|
Tabelul
2.7. Tabelul ANOVA la regresia multipla
Testul
de semnificatie globala a regresiei se formuleaza astfel: exista
cel putin o variabila explicativa semnificativa?
Ipotezele sunt:
H0:
a1 = a2 = = ak
= 0 (toti coeficientii
sunt nuli, nici o variabila explicativa nu isi
aduce
contributia la explicarea variabilei y;
termenul constant a0 nu
prezinta interes, deoarece un model in care numai termenul constant este
semnificativ, nu are sens economic.)
H1: exista cel putin un coeficient nenul.
In cazul in care se
accepta H0 inseamna ca nu exista nici o
relatie liniara semnificativa intre variabila y si variabilele xi cu i=1,2, , k. Testarea ipotezei nule este echivalenta cu a
testa daca varianta SSE este semnificativ diferita de 0.
In
cazul exercitiului prezentat, tabelul de analiza variantei pentru
modelul cu doua variabile explicative, dupa eliminarea variabilei
nesemnificative x3, este
extras din Tabelul 2.6, in Tabelul 2.8:
|
Natura variatiei
|
df
|
SS
|
MS
|
F
|
Significance F
|
|
Regression
|
|
|
|
|
|
|
Residual
|
|
|
|
|
|
|
Total
|
|
|
|
|
|
Tabelul
2.8. Tabelul ANOVA pentru modelul cu doua variabile explicative
Ipoteza
de normalitate a erorilor implica sub ipoteza H0, ca
statistica F* urmeaza o lege
Fisher cu k si n-k-1 grade de libertate. 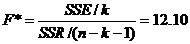 se compara cu o
valoare teoretica Fisher cu 2 si 11 grade de libertate, care pentru
un prag de semnificatie a=5% este
se compara cu o
valoare teoretica Fisher cu 2 si 11 grade de libertate, care pentru
un prag de semnificatie a=5% este 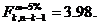 Cum
Cum 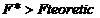
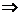 se accepta
ipoteza alternativa, H1, deci regresia este global
semnificativa, modelul este bine construit. Valoarea calculata F* corespunde unui prag de
semnificatie de 0.16%, mult mai mic decat 5%.
se accepta
ipoteza alternativa, H1, deci regresia este global
semnificativa, modelul este bine construit. Valoarea calculata F* corespunde unui prag de
semnificatie de 0.16%, mult mai mic decat 5%.
Si regresia prezentata in
Tabelul 2.5, cu trei variabile explicative, este global semnificativa
pentru ca 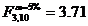 , iar valoarea calculata F*=7.87>3.71, pentru un prag de semnificatie de 0.54%.
, iar valoarea calculata F*=7.87>3.71, pentru un prag de semnificatie de 0.54%.
Numai
cand modelul are termen constant, F*
se poate scrie in functie de coeficientul de determinatie R2. Din relatia 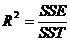 , se poate exprima
, se poate exprima 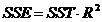 , iar SSR se poate
exprima in functie de coeficientul de nedeterminatie
, iar SSR se poate
exprima in functie de coeficientul de nedeterminatie 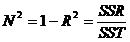 ,
, 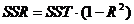 .
.
Inlocuind
in formula statisticii F*, valorile
astfel exprimate SSE si SSR, se simplifica cu SST si ramane astfel: 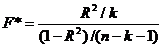 .
.
Pe
langa testul global de semnificatie, se efectueaza testele de
semnificatie individuala a coeficientilor pentru fiecare variabila
explicativa din model.
Calitatea
ajustarii se determina in functie de coeficientul de determinatie:
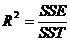 . Daca
. Daca 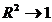 inseamna varianta
totala SST, este aproape in intregime explicata SSE, modelul este
bine ales. Coeficientul de determinatie multipla:
inseamna varianta
totala SST, este aproape in intregime explicata SSE, modelul este
bine ales. Coeficientul de determinatie multipla: 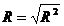 , arata intensitatea corelatiei simultane a
variabilelor explicative asupra variabilei dependente y.
, arata intensitatea corelatiei simultane a
variabilelor explicative asupra variabilei dependente y.






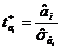 , se compara cu valoarea teoretica Student pentru
, se compara cu valoarea teoretica Student pentru 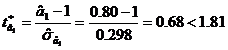 . Se accepa ipoteza nula, coeficientul a1 nu este semnificativ
inferior valorii 1.
. Se accepa ipoteza nula, coeficientul a1 nu este semnificativ
inferior valorii 1.