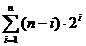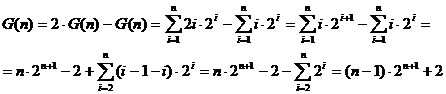Complexitatea algoritmilor

Teoria complexitatii are ca obiect de studiu clasificarea problemelor, bazata pe timpul de executie si spatiul de lucru utilizat de algoritmi pentru solutionarea lor. Cind se analizeaza algoritmi paraleli, se poate lua in considerare si numarul de procesoare.

Desi teoria complexitatii a fost dezvoltata pentru probleme de decizie, aceasta nu este o restrictie severa deoarece multe alte probleme pot fi formulate in termeni de probleme de decizie. De exemplu o problema de optimizare poate fi rezolvata prin punerea intrebarii existentei unei solutii cu cel mult sau cel putin o valoare specificata.

Masurarea complexitatii

Complexitatea timpului de executie a unui algoritm paralel care rezolva o instanta de dimensiune n a unei probleme, pe o masina paralela cu p procesoare (p=dimensiunea masinii) se noteaza a cu T(p,n)=T_p(n).

O problema se numeste dependenta de dimensiunea masinii (PDD) daca n este o functie de variabila p. Altfel, problema se numeste independenta de dimensiunea masinii (PID). Un algoritm dependent de dimensiunea masinii este un algoritm ce rezolva o problema PDD. altfel, algoritmul se numeste independent de dimensiunea masinii.

Factorul de incarcare (L) a unei probleme este raportul n/p. Viteza S_p(n)) unui algoritm paralel este raportul T₁(n)/T_p(n). Eficienta (E_p(n)) unui algoritm paralel se defineste ca fiind raportul dintre viteza si numarul procesoarelor:

E _p(n)=S_p(n)/p=T₁(n)/[p T_p(n)].

Pentru a aprecia comportarea asimtotica a functiei T_p(n) se utilizeaza urmatoarele notiuni:

Fiind date doua functii f si g pozitive de variabile p si n se noteaza :

o(g)= N] a.i.( )[(p>p₀) (n>n₀(p))]: f(p,n)<e g(p,n)}

Rezulta ca f este in o(g) daca lim_n (f/g)=0.

O(g)= N cIR ] a.i.( )[(p>p₀) ) (n>n₀(p))]: f(p,n)<c g(p,n)}

Deci f este in O(g) daca functia f/g este marginita.

Q(g)= N R ] a.i.( )[(p>p₀) ) (n>n₀(p))]: 0<c₁ g(p,n)<f(p,n)<c₂ g(p,n)}

Aceasta inseamna ca fIQ(g) daca f/g este o functie strict pozitiva si marginita.

W(g)= N cIR ] a.i.( )[(p>p₀) ) (n>n₀(p))]: 0<c g(p,n)<f(p,n)}

Rezulta ca fIW(g) daca f/g este marginita inferior de o valoare strict pozitiva.

Clase de complexitate

Din punctul de vedere al calculului secvential, 3 clase sint relevante: P, NP, Pspace

Clasa P contine problemele solvabile in timp polinomial ceea ce inseamna ca pentru aceste probleme exista algoritmi deterministi secventiali cu timpul de executie marginit de un polinom de variabila 'dimensiunea problemei '. Problemele din P sint numite, in mod curent, bine solutionabile sau usoare.

NP este clasa problemelor pentru care exista un algoritm sevential nedeterminist cu timp de executie polinomial (echivalent : nu exista un algoritm secvential determinist cu timp de executie polinomial.)

Pspace contine problemele care sint solvabile utilizind un spatiu polinomial, adica spatiul de lucru este marginit de un polinom de variabila ' dimensiunea problemei '.

Evident, P NP Pspace . Se presupune ca ambele incluziuni sint proprii (stricte).

O alta clasa inclusa in Pspace, neinteresanta din punct de vedere al calculului secvential, dar importanta pentru calculul paralel este Polylogspace. Aici sint incluse problemele rezolvabile in spatiu polilogaritmic (spatiul de lucru este marginit de un polinom de variabila 'log(dimensiunea problemei)'). Multe probleme din P apartin lui Polylogspace, dar in general, se crede ca P Polylogspace. Se stie totusi ca Polylogspace Pspace .

Remarcabile in Pspace si NP sint problemele complete.Problemele Pspace-complete sint generalizari ale tuturor celorlalte probleme din Pspace in termeni de transformari care necesita timp polinomial. Mai precis: o problema este Pspace-completa sub transformari de timp polinomial daca apartine lui Pspace si oricare alta problema din Pspace este reductibila la ea prin transformari care necesita timp polinomial. Urmeaza ca daca o problema Pspace-completa ar apartine lui P atunci Pspace = P. Deoarece se crede ca aceasta egalitate nu este adevarata, este improbabil sa existe un algoritm de timp polinomial pentru o problema Pspace-completa. Problemele NP se definesc in mod asemanator, rezultind aceleasi concluzii.

Clasa P are si ea problemele ei complete. Problemele P-complete sint generalizari ale tuturor celorlalte probleme din clasa P, in termenii transformarilor care necesita spatiu de lucru logaritmic. Formal, o problema este P-completa sub transformari spatiale logaritmice daca apartine clasei P si orice alta problema din P este reductibila la ea prin transformari ce utilizeaza spatiu logaritmic. Daca o problema P-completa ar apartine clasei Polylogspace, atunci ar fi adevarata incluziunea P Polylogspace. Cum aceasta incluziune se presupune a fi falsa, nu este de asteptat sa existe un algoritm pentru o problema P-completa care sa utilizeze spatiu de lucru polilogaritmic.

Teze

Relatia intre calculul secvential si paralel este data de teza calculului paralel (Chandra, Kozen & Stockmeyer, 1981; Goldshlager, 1982): pentru orice functie T(n), (n= dimensiunea problemei), clasa problemelor solvabile de o masina cu paralelism nemarginit in timp T(n)^O(1) (polinomial in T(n) ) este egala cu clasa problemelor solvabile de masini secventiale cu spatiu (T(n))^O(1) .

Aceasta teza este o teorema pentru multe dintre modelele relativ rezonabile. Astfel, clasa problemelor solvabile in T(n)^O(1) timp de o masina PRAM este egala cu clasa problemelor solvabile cu T(n)^O(1) spatiu de lucru de o masina Turing, daca T(n) log n (Fortune & Wyllie, 1978). In consecinta, clasa problemelor solvabile de o masina PRAM in timp paralel polinimial este egala cu clasa Pspace. De asemenea, Polylogspace este clasa problemelor solvabile de o masina PRAM in timp paralel polilogaritmic.

Problemele din P Polylogspace sint solvabile in timp paralel polilogaritmic. Ele pot fi considerate cele mai usoare probleme din P, in sensul ca influenta dimensiunii problemei asupra timpului de rezolvare a fost redusa la minimum. O reducere ulterioara a a timpului de solutionare la dimensiuni sublogaritmice este, in general, imposibila. Una din ratiunile acestei afirmatii este aceea ca o masina PRAM necesita O(log n) timp pentru activarea a n procesoare.

Pe de alta parte, este improbabil ca problemele P-complete sa admita solutii in timp polilogaritmic. Daca o astfel de problema ar fi rezolvabila in timp paralel polilogaritmic ar urma ca apartine clasei Polylogspace si astfel ar fi adevarata incluziunea P Polylogspace. Din acest motiv, nu este de asteptat o solutie in timp paralel polilogaritmic. Orice metoda de rezolvare pentru problemele grele din P necesita probabil timp superlogaritmic si aceasta deoarece natura lor este probabil inerent secventiala. Aceasta nu inseamna insa ca paralelismul nu poate aduce cresteri substantiale de viteza, algoritmilor de rezolvare.

In concluzie, clasa P poate fi partitionata in probleme foarte usoare (very easy) care sint rezolvabile in timp paralel polilogaritmic si probleme mai putin usoare (not so easy), pentru care este improbabila cresterea vitezei prin paralelism.

Complexitatea algoritmilor secventiali

La evaluarea (estimarea) algoritmilor secventiali se pune in evidenta necesarul de timp si de spatiu de memorare.

Studierea complexitatii presupune analiza completa in cadrul algoritmului a urmatoarelor 3 aspecte:

configuratia de date cea mai defavorabila (cazurile degenerate);

configuratia de date cea mai favorabila;

comportarea medie.

Comportarea medie presupune probabilitatea de aparitie a diferitelor configuratii de date la intrare.

Aspectul 1 este cel mai studiat si este folosit, de obicei, pentru compararea algoritmilor secvetiali.

Complexitatea unui algoritm secvential se exprima de regula in limbajul ordinului O.

Definitie

Fie f : N N si g : N N doua functii.

Spunem ca fI O(g) si notam f = O(g) daca si numai daca o constanta cI R₊ si un numar

n₀I N astfel incat pentru n > n₀ f(n) < c g(n)

Observatie:

n reprezinta de obicei dimensiunea datelor de intrare iar f(n) timpul de lucru al algoritmului exprimat in 'pasi'.

Lema:

Daca f este o functie polinomiala de grad k, de forma:

f(n) = a_k n^k + a_k-1 n^k-1 + + a₁ n + a₀, atunci f = O(n^k).

Facindu-se majorari in membrul drept, obtinem rezultatul de mai sus:

f(n) <= a_k n^k + a_k-1 n^k-1 + + a₁ n + a₀ < n^k· a_k a_k-1 a₀ < n^k c pentru n > 1 T f(n) < c n^k, cu n₀ = 1.

Concluzie: f = O(n^k), si ordinul O exprima viteza de variatie a functiei, functie de argument.

Exemplul 1: Calcularea maximului unui sir

Max_Sir (A,n)

Daca notam cu T(n) timpul de executie in pasi al acestui algoritm atunci T(n)= 1 + 2(n-1) = numarul de atribuiri si comparatii

Cazul cel mai defavorabil: situatia in care vectorul este ordonat crescator (pentru ca de fiecare data se face si comparatie si atribuire).

Putem spune ca T(n) = O(n), este o functie polinomiala de gradul I. Conteaza doar ordinul polinomului, nu coeficientul termenului de grad maxim, iar la numararea pasilor ne concentram asupra numarului buclelor, nu asupra pasilor din interiorul buclei.

Exemplul 2: Insertion Sort (algoritmul de sortare prin inserare)

Algoritmul INSERTION SORT considera ca in pasul k, elementele A[1÷k‑1] sunt sortate, iar elementul k va fi inserat, astfel incat, dupa aceasta inserare, primele elemente A[ 1÷k] sa fie sortate.

Pentru a realiza inserarea elementului k in secventa A[1÷k‑1], aceasta presupune:

memorarea elementului intr‑o varibila temporara;

deplasarea tuturor elementelor din vectorul A[1÷k‑1] care sunt mai mari decat A[k], cu o poziie la dreapta (aceasta presupune o parcurgere de la dreapta la stanga);

plasarea lui A[k] in locul ultimului element deplasat.

Complexitate: O(n)

Insertion_Sort (A,n)

A[i+1] = temp;

Cazul cel mai dafavorabil: situatia in care deplasarea (la dreapta cu o pozitie in vederea inserarii) se face pana la inceputul vectorului, adica sirul este ordonat descrescator.

Exprimarea timpului de lucru:

T(n) = 3·(n - 1) +3·(1 + 2 + 3+ + n - 1) = 3(n-1) + 3n (n - 1)/2

Rezulta complexitatea: T(n) = O(n²) functie polinomiala de gradul II.

Observatie: Cand avem mai multe bucle imbricate, nivelul buclei celei mai interioare dau gradul polinomului egal cu ordinul de complexitate al algoritmului.

Bucla cea mai interioara ne da complexitatea algoritmului.

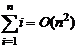
Exemplul 3 Inmultirea a doua matrici

Prod_Mat (A,B,C,n);

Rezulta complexitatea O(n³).

Exemplul 4 Cautarea binara (Binary Search)

Fie A, de ordin n, un vector ordonat crescator. Se cere sa se determine daca o valoare b se afla printre elementele vectorului. Limita inferioara se numeste low, limita superioara se numeste high, iar mijlocul virtual al vectorului, mid (de la middle).

Binary_Search (A,n,b)

return(0)

Calculul complexitatii algoritmului consta in determinarea numarului de ori pentru care se executa bucla while.

Se observa ca, la fiecare trecere, dimensiunea zonei cautate se injumatateste. Cazul cel mai defavorabil este ca elementul cautat sa nu se gaseasca in vector.

Pentru simplitate se considera n = 2^k unde k este numarul de injumatatiri. Rezulta k = log₂ n si facand o majorare, T(n) log₂ n +

Deci complexitatea timp a acestui algoritm este O(log₂n). Baza logaritmului se poate ignora deoarece: log_ax = log_ab log_bx si log_ab este o constanta, deci ramine O(log n), adica o functie logaritmica.

Proprietati ale ordinului de complexitate O:

1) Fie f, g : N N

Daca f = O(g) T | k f = O(g)

| f = O(k g) , k I R

2) Fie f, g, h : N N.

si: f = O(g) |

g = O(h) | T f = O(h)

3) Fie f₁, f₂, g₁, g₂ : N N

si: f₁ = O(g₁) | T | f₁ + f₂ = O(g₁ + g₂)

f₂ = O(g₂) | T | f₁ f₂ = O(g₁ g₂)

Aceasta proprietate permite ca, atunci cind avem doua bucle imbricate (de complexitati diferite), complexitatea totala sa se obtina inmultindu-se cele doua complexitati. Cele doua complexitati se aduna, daca buclele sunt succesive.

Teorema

Oricare ar fi doua constante c > 0, a > 1, si f : N N, o functie monotona strict crescatoare, atunci    (f(n))^c = O(a^f(n))

Demonstratia se bazeaza pe limita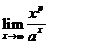

Intre ordinul functiilor polinomiale si cel al functiilor exponentiale exista relatia: O(n^c) O(aⁿ)

Au loc urmatoarele incluziuni:

O(1) O(log n) O(log^k n) O(n) O(n log n) O(n²) O(n^k log n) O(n^k+1) O(2ⁿ)

Pentru calculul complexitatii se va incerca incadrarea in clasa cea mai mica de complexitate din acest sir:

O(1) clasa algoritmilor constanti;

O(log n) clasa algoritmilor logaritmici;

O(log^k n) clasa algoritmilor polilogaritmici;

O(n log n)    

O(n) clasa algoritmilor liniari;

O(n²) clasa algoritmilor patratici;

O(n^k+1) clasa algoritmilor polinomiali;

O(n log^kn)

O(2ⁿ) clasa algoritmilor exponentiali.

Tehnici de calcul a complexitatii

Se folosesc urmatoarele sume:

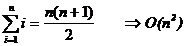
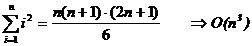
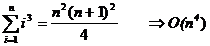
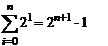
Sa calculam, de exemplu, suma: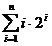 

Se noteaza:

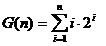
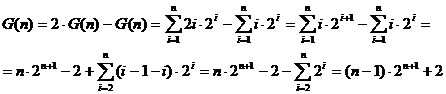
Prin aceeasi tehnica se calculeaza suma: