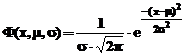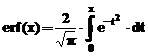Cautarea datelor in tabele
a.) Cautarea datelor in tabele unidimensionale
Cautarea
datelor in tabele este o operatiune utila in situatiile in care
sunt necesare verificari ale elementelor unei matrici sau unei serii de
elemente ordonate crescator in prima coloana. Versiunile anterioare
versiunii MATLAB 5.3 dispun de o functie specifica de cautare in
tabele, functia table1(tabel, xi),
in timp ce, versiunile recente ale MATLAB dispun functii specifice care
realizeaza aceasta operatiune (de cautare in tablouri de
date) prin interpolare. Tabelul de date trebuie sa fie organizat ca o
matrice astfel incat in prima coloana se gasesc valorile lui x (abscisa ordonata
crescator) iar in celelalte coloane sunt valorile y corespunzatoare, printre care pot fi cautate valori intermediare.
Obs.:
Daca x se gaseste intre
doua valori din tabel functia table1() returneaza o valoare
interpolata liniar;
Functia MATLAB table1() este inlocuita in versiunile superioare
ale MATLAB(ulterioare versiunii 5.3) cu functiile interp1(),interp2(), interp3(), interpft(), interplat(), interplon(), interpm(), interpn().
Ex.:
Fiind date perechile de numere (x,y) : (-2,6); (-1,2); (0,3); (2,1); (4,7) ,se cere
sa se gaseasca valorile y
corespunzatoare pentru x1 =
-1; x2 = 3; x3 = 3.5; x4 = 0.5; x5 = 3.75; x6 = -0.573.
Solutie:
-se organizeaza perechile de numere (x,y) ca matrice cu 2 coloane,
apoi se foloseste functia table1(),
pentru a gasi valorile cerute:
» tablou_original =[-2,6; -1,2; 0,3; 2,1;
4,7];
»y1= table1(tablou_original,-1)
y1 = 2
»y2=table1(tablou_original,3)
y2 = 4
»y3=table1(tablou_original,3.5)
y3 = 5.5
»y4=table1(tablou_original,0.5)
y4 = 2.5
»y5=table1(tablou_original,3.75)
y5 =
6.25
»y6=table1(tablou_original,-0.573)
y6 =
2.427
Atentie !
Coloana
I trebuie sa fie monotona (elementele trebuie sa fie ordonate
crescator) !
Valorile cautate trebuie sa se incadreze
intre cea mai mica si cea mai mare valoare a lui x, altfel, se
afiseaza un mesaj de eroare. Astfel, daca se cere sa se
gaseasca valoarea corespunzatoare lui y atunci cand x=5, MATLAB
afiseaza urmatorul mesaj :
» y7=table1(tablou_original,5)
??? Error using ==> table1
x0
larger than all values in first column
???Eroare
la utilizarea ==> table1
x0
este mai mare decat toate valorile primei coloane
b.) Cautarea datelor in tabele
bidimensionale
In cazul
tablourilor de valori bi- dimensionale (aceste tablouri se caracterizeaza
prin urmatoarea particularitate:elementele sunt aranjate dupa
doua directii x si y, acestei perechi ii corespunde o a
treia valoare z ), functia
MATLAB utilizata pentru cautarea valorilor z corespunzatoare unei perechi (x,y) este:
»table2("tab",x,y)
Obs.:
Functia MATLAB table2() este inlocuita in versiunile superioare
versiunii MATLAB 5.3 cu functia interp2(), in linia de comanda a
versiunilor superioare ale MATLAB apare mesajul de avertizare : "Warning: TABLE2 is obsolete and will be
removed in future versions. Use INTERP2
instead." ("Atentie:TABLE2 este depasita si va fi
inlocuita in viitoarele versiuni. Folositi INTERP2 pentru acelasi scop!")
Conditii:
-tabelul "tab"
este organizat ca o matrice, cu n linii
si m coloane, intotdeauna
avand, pe pozitia (1,1),
elementul 0 ;
-numarul de linii este dat de numarul
valorilor argumentului x, la care se
adauga o linie pentru introducerea valorilor argumentului y, iar numarul de coloane este dat
de numarul valorilor lui y;
-valorile x-ilor
se plaseaza pe prima coloana, in ordine crescatoare, incepand
cu a 2-a linie;
-valorile y-ilor
se plaseaza pe prima linie, in ordine crescatoare, incepand
cu a 2-a coloana;
Celelalte elemente ale matricei sunt valorile z (obtinute prin masuratori,
calcule, etc.).
Ex. :
Fiind date
tripletele:
Sa se gaseasca valorile corespunzatoare perechilor (x,y): (-3,7); (-3,6.5); (-2,6); (50,8); (99,9.9); (-4,8); (2,11).
Solutie:
»tablou_original_2= [0,1,2,3,4,5,6,7,8,9,10;-3,0,1,2,4,8,7,11,0,1,1;
2,9,3,1,7,6,5,3,1,0,-3;8,-8,9,1,0,2,-8,2,1,0,1;
100,0,0,1,7,2,8,1,2,1,10] ;
»z1=table2(tablou_original_2,-3,7)
z1=11
»z2=table2(tablou_original_2,-3,6.5)
z2=9
»z3=table2(tablou_original_2,-2,6)
z3=6.6
»z4=table2(tablou_original_2,50,8)
z4=1.4565
»z5=table2(tablou_original_2,99,9.9)
z5=0.1087
»z6=table2(tablou_original_2,-4,8)
??? Error using ==> table2
x0 smaller than all values in first column
??? Eroare la utilizarea ==> table2
x0 este inferioara
valorilor din prima coloana
»z7=table2(tablou_original_2,2,11)
???
Error using ==> table2
x0
larger than all values in first column
??? Eroare la utilizarea ==> table2
x0 este superioara
valorilor din prima coloana
interpolarea si Regresia
In foarte multe aplicatii practice apare necesitatea
evaluarii aproximative a unei functii 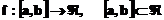 . Problema aproximarii functiilor
intervine in situatii de o mare
diversitate, multitudinea formularilor si metodelor de
rezolvare asociate constituind o reflectare directa a acestei
diversitati.
. Problema aproximarii functiilor
intervine in situatii de o mare
diversitate, multitudinea formularilor si metodelor de
rezolvare asociate constituind o reflectare directa a acestei
diversitati.
In aplicatii este frecvent necesara utilizarea unor functii
pentru care sunt
cunoscute doar valorile corespunzatoare unui set discret de valori ale argumentelor. Astfel de dependente pot
reprezenta, spre exemplu, tabelarea unor
functii matematice sau a unor marimi fizice masurate sau
calculate. Pentru simplitatea discutiei ne limitam in cele ce
urmeaza la functii reale de o
variabila reala. In toate
cazurile, pentru functia considerata 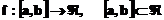 sunt specificate valorile
sunt specificate valorile 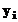 intr-un numar de puncte de
retea
intr-un numar de puncte de
retea 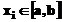 , adica
, adica
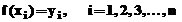
Prelucrarea numerica
ulterioara a acestor functii impune adesea si utilizarea unor
valori corespunzatoare unor argumente diferite de cele tabelate. In multe situatii, insa,
obtinerea unor informatii suplimentare este dificila, daca nu
chiar imposibila. Astfel, chiar daca este cunoscut algoritmul de
calcul al functiei, complexitatea acestuia poate face uneori
ineficienta utilizarea lui pentru detalierea iuformatiei. Pe de alta
parte, daca valorile tabelate provin din observatii, ele sunt, in
general, afectate de erori de masura.
In toate situatiile mentionate, pentru a sintetiza
informatia asupra functiei tabelate f si a o putea utiliza eficient in calcule, se impune
aproximarea ei printr-o functie continua, numita functie
model, 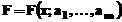 care
depinde
in general de un numar de parametri
ajustabili, aj,-, numiti parametri de model. Forma
functiei F si valorile parametrilor aj trebuie determinate astfel incat
functia discreta f sa
fie aproximata optim intr-un anumit sens.
care
depinde
in general de un numar de parametri
ajustabili, aj,-, numiti parametri de model. Forma
functiei F si valorile parametrilor aj trebuie determinate astfel incat
functia discreta f sa
fie aproximata optim intr-un anumit sens.
Alegerea formei concrete a
functiei model F este o problema
netriviala si ea trebuie sa aiba la baza o
fundamentare riguroasa. In linii
mari, stau la dispozitie urmatoarele optiuni:
functia
model se alege dintr-o clasa convenabila de functii (cum
ar fi: polinoame, functii gaussiene etc.), care ofera simplitate si
eficienta in prelucrari ulterioare;
functia
model este derivata dintr-o teorie, in cadrul careia parametrii de model au
o semnificatie bine stabilita;
functia
model rezulta dintr-un compromis intre
constrangerile si avantajele optiunilor anterioare.
Pentru a putea determina practic
valorile optime ale parametrilor de model, trebuie definita o functionala
care sa reflecte gradul in care functia model F aproximeaza
functia tabelata f pentru o alegere particulara,
a parametrilor. Admitand ca f si F apartin spatiului 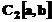 al functiilor de
patrat sumabil pe [a,b], o
masura sugestiva a abaterii modelului fata de
functia modelata este data de distanta dintre
cele doua functii:
al functiilor de
patrat sumabil pe [a,b], o
masura sugestiva a abaterii modelului fata de
functia modelata este data de distanta dintre
cele doua functii:
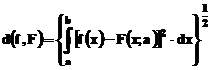
unde s-a
utilizat notatia vectoriala 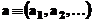 Evident, aceasta definitie nu este
utilizabila ca atare, deoarece implica si cunoasterea
expresiei analitice a functiei f. Se poate utiliza, insa, o
definitie mai putin riguroasa, dar aplicabila. pentru functii discrete:
Evident, aceasta definitie nu este
utilizabila ca atare, deoarece implica si cunoasterea
expresiei analitice a functiei f. Se poate utiliza, insa, o
definitie mai putin riguroasa, dar aplicabila. pentru functii discrete:
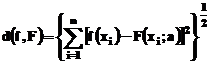
Aproximarea pe baza acestei
distante este numita aproxirnare in medie patratica
ssi este utilizata in douaa dintre cele mai importante metode de mode-lare a functiilor
tabelate: mterpolarea si regresia.
Daca, valorile tabelate 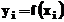 sunt
considerate exacte (neafectate de erori), este firesc sa se impuna anularea distantei
dintre functiile f si F
sunt
considerate exacte (neafectate de erori), este firesc sa se impuna anularea distantei
dintre functiile f si F
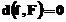
Aceasta revine la construirea unei
functii model, apartinand unei anumite clase, care sa ia, in punctele de tabelare 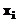 , aceleasi valori
ca si functia f(x)
, aceleasi valori
ca si functia f(x)

Functia care satisface aceste
conditii este utilizata, in mod normal, pentru aproximarea
functiei f(x) pe
intervalul 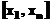 iar procedeul se
numeste interpolare Functia
iar procedeul se
numeste interpolare Functia
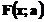 poarta
numele de functie de interpolare
sau interpolant iar nodurile
poarta
numele de functie de interpolare
sau interpolant iar nodurile
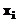 se mai numesc
si puncte de interpolare Geometric, interpolarea
implica gasirea unei curbe
se mai numesc
si puncte de interpolare Geometric, interpolarea
implica gasirea unei curbe 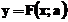 care trece
prin toate punctele
care trece
prin toate punctele 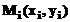 . De exemplu, presupunand functia y=sinx, reprezentata grafic in
punctele
. De exemplu, presupunand functia y=sinx, reprezentata grafic in
punctele 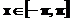 , interpolarea in sapte
puncte echidistante, ale intervalului, este realizata cu o
functie MATLAB specifica, si surprinsa in imaginea alaturata.
, interpolarea in sapte
puncte echidistante, ale intervalului, este realizata cu o
functie MATLAB specifica, si surprinsa in imaginea alaturata.
Daca, argumentele
pentru care se evalueaza interpolantul se afla inafara intervalului 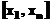 procedeul
se numeste extrapolare.
procedeul
se numeste extrapolare.
Cu un asemenea enunt, general insa, problema poate
avea o infinitate de solutii sau nici una, in functie de clasa careia ii
apartine functia model.
 Problema interpolarii devine neambigua daca
in locul unei functii model arbitrare
cautam un polinom Pm(x)
de grad nu mai mare decat (n - 1),
care satisface conditiile de interpolare. Din acest
set de conditii se pot determina cei (m+1)
coeficienti ai polinomului si metoda se numeste interpolare
polinomiala.Functiile de interpolare polinomiale sunt cele mai
utilizate in practica. Dintre
acestea amintim functia
Lagrange si interpolantii spline si Akima (netezi pe portiuni). Totusi, in anumite cazuri se dovedesc utile si functiile de interpolare
rationale. La randul lor, functiile trigonometrice conduc la asa-numita
interpolare trigonometrica, si la metodele Fourier inrudite.
Problema interpolarii devine neambigua daca
in locul unei functii model arbitrare
cautam un polinom Pm(x)
de grad nu mai mare decat (n - 1),
care satisface conditiile de interpolare. Din acest
set de conditii se pot determina cei (m+1)
coeficienti ai polinomului si metoda se numeste interpolare
polinomiala.Functiile de interpolare polinomiale sunt cele mai
utilizate in practica. Dintre
acestea amintim functia
Lagrange si interpolantii spline si Akima (netezi pe portiuni). Totusi, in anumite cazuri se dovedesc utile si functiile de interpolare
rationale. La randul lor, functiile trigonometrice conduc la asa-numita
interpolare trigonometrica, si la metodele Fourier inrudite.
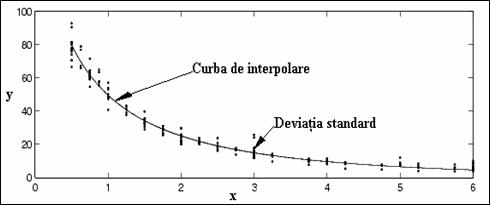 Daca valorile tabelate
Daca valorile tabelate 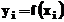 provin din
observatii, ele sunt afectate in general de
erori de masurare, imprecizia fiecarei valori fiind
specificata de obicei prin deviatia
standard
provin din
observatii, ele sunt afectate in general de
erori de masurare, imprecizia fiecarei valori fiind
specificata de obicei prin deviatia
standard 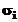 asociata:
asociata:
In astfel de cazuri, functia model F = F(x; a) este cu atat mai
buna cu cat sunt mai elaborate considerentele pe baza carora i s-a
stabilit forma (cu cat este mai putin empirica). Avand in vedere imprecizia
datelor, nu este de asteptat ca functia model sa interpoleze punctele
tabelate (chiar daca acest lucru este teoretic posibil) si este deci firesc sa se impuna minimizarea
distantei d(f, F)
in raport cu valorile parametrilor:
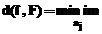
nu anularea
ei riguroasa ca in cazul interpolarii. In mod concret, aceasta revine la
determinarea celor m parametri,
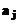 , ai functiei model F(x; a),
apartinand unei anumite clase, care minimizeaza suma abaterilor
patratice punctuale ale functiei model fata de datele
tabelate:
, ai functiei model F(x; a),
apartinand unei anumite clase, care minimizeaza suma abaterilor
patratice punctuale ale functiei model fata de datele
tabelate:
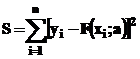
Acest
procedeu se numeste regresie sau ajustare prin metoda celor mai mici patrate. Termenul preluat din limba engleza este fitare (de la 'to fit'-a potrivi), desemnand procesul de ajustare a
parametrilor curbei de regresie.
Intr-un context mai larg,
functionala 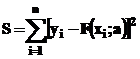 reprezinta
asa-numita functie de merit a procesului
de ajustare. Pentru o apreciere mai nuantata a gradului in care
functia model aproximeaza datele masurate, in practica se
utilizeaza functii de merit mai
elaborate. Oricum, deoarece in mod conventional functia de merit
este construita astfel incat valori mici sa corespunda unor abateri reduse ale
modelului fata de functia tabelata, procesul de ajustare a
parametrilor de model este, in esenta., un proces de minimizare multidimensiona. Unul dintre
cele mai utilizate criterii de performanta este cel furnizat de functia de merit 'hi-patrat'
reprezinta
asa-numita functie de merit a procesului
de ajustare. Pentru o apreciere mai nuantata a gradului in care
functia model aproximeaza datele masurate, in practica se
utilizeaza functii de merit mai
elaborate. Oricum, deoarece in mod conventional functia de merit
este construita astfel incat valori mici sa corespunda unor abateri reduse ale
modelului fata de functia tabelata, procesul de ajustare a
parametrilor de model este, in esenta., un proces de minimizare multidimensiona. Unul dintre
cele mai utilizate criterii de performanta este cel furnizat de functia de merit 'hi-patrat'
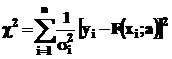
Spre deosebire de functionala 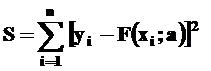 functia
de merit 'hi-patrat', atribuie
ponderi diferite punctelor de tabelare individuale, si anume
depinzand de inversul deviatiei standard
functia
de merit 'hi-patrat', atribuie
ponderi diferite punctelor de tabelare individuale, si anume
depinzand de inversul deviatiei standard 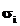 asociate.
In acest fel creste ponderea
relativa a punctelor afectate de erori mici, functia model fiind
fortata in procesul
ajustarii parametrilor sa minimizeze cu
precadere distanta fata de aceste puncte in detrimentul distantei fata
de punctele mai imprecise (cu
asociate.
In acest fel creste ponderea
relativa a punctelor afectate de erori mici, functia model fiind
fortata in procesul
ajustarii parametrilor sa minimizeze cu
precadere distanta fata de aceste puncte in detrimentul distantei fata
de punctele mai imprecise (cu 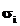 mari).
In cazul in care deviatiile
mari).
In cazul in care deviatiile 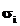 sunt egale sau nu sunt cunoscute,
formalismul se simplifica si revine la regresia cu ajutorul functiei de merit S. Extremum- ul
functionalei
sunt egale sau nu sunt cunoscute,
formalismul se simplifica si revine la regresia cu ajutorul functiei de merit S. Extremum- ul
functionalei 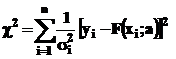 in raport cu parametrii aj este caracterizat prin relatiile:
in raport cu parametrii aj este caracterizat prin relatiile:
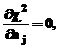 j=1, 2, . , m
j=1, 2, . , m
sau
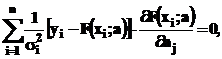 j=1, 2, . , m
j=1, 2, . , m
din care pot fi determinati parametrii aj. Ajustarea pe baza
functiei de merit 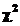 mai este numita
uneori si regresie
'hi-p&trat'.
mai este numita
uneori si regresie
'hi-p&trat'.
Curba de regresie y = F(x;a.) nu trebuie sa treaca in mod necesar prin nici unul din punctele tabelate Mi(xi, yi), ci doar
prin barele de eroare ale acestora (de
lungime 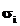 ), minimizand functionala
), minimizand functionala 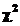 .
.
Deoarece erorile de masurare ale
datelor induc imprecizii in determinarea
parametrilor
de model, informatia furnizata de procesul de ajustare nu este completa
fara estimarea acestor erori. Admitand ca datele sunt
independente, considerente de propagare a erorilor arata. ca varianta
(imprecizia probabila patratica.) 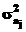 asociata
parametrului aj rezulta
prin cumularea contributiilor ponderate cu
asociata
parametrului aj rezulta
prin cumularea contributiilor ponderate cu
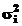 de la
fiecare valoare discreta yi
de la
fiecare valoare discreta yi
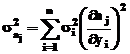
Cresterea fara o
justificare teoretica clara a numarului de parametri de model in
ideea descrierii cat mai exacte a datelor, eventual chiar a interpolarii lor, nu face
functia model 'mai buna' chiar daca reduce valoarea
functiei de merit, ci, pe langa lipsa de semnificatie a
modelului si a parametrilor adaugati, poate conduce la
aparitia unor fenomene numerice greu de controlat. Interpolarea
nu trebuie privita deci, in nici un
caz, ca o limita ideala a regresiei, cele doua metode de
aproximare avand semnificatii diferite si fiind aplicabile in situatii distincte.
In
general, datele experimentale reprezinta valori discrete determinate prin
diferite metode. Aceste date pot reprezenta analitic o relatie
matematica dintre diferitele date experimentale observate si se
exprima prin functii ai caror coeficienti se
determina, in general, prin rezolvarea unor sisteme de ecuatii
lineare. De exemplu, considerand ca s-au masurat, la momentele t = [0 .3 .8 1.1 1.6 2.3]', valorile y = [0.5 0.82 1.14 1.25 1.35 1.40]', se
reprezinta grafic dependenta y(t)
al carei grafic este o curba convexa.
Metoda celor mai mici patrate
Majoritatea
metodelor de aproximare, ajustare, interpolare sau extrapolare, utilizeaza
ca metoda de calcul a coeficientilor, metoda celor mai mici patrate. Aceasta metoda
minimizeaza suma patratelor reziduurilor: 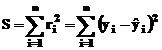 . Reziduum-ul este calculat ca diferenta dintre valoarea
"observata"
. Reziduum-ul este calculat ca diferenta dintre valoarea
"observata" 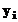 si valoarea
previzionata
si valoarea
previzionata 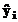 :
: 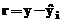 . MATLAB recunoaste patru tipuri de metode aplicative
variante ale metodei celor mai mici patrate:
. MATLAB recunoaste patru tipuri de metode aplicative
variante ale metodei celor mai mici patrate:
Metoda lineara a celor mai mici patrate;
Metoda ponderata a celor mai mici
patrate;
Metoda robusta a celor mai mici
patrate;
Metoda nelineara a celor mai mici
patrate.
Metoda linearA a celor
mai mici patrate
Aceasta
metoda foloseste un model matematic linear (o functie de gradul
intai) pentru aproximarea datelor: 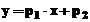 , in care cei doi coeficienti urmeaza a fi
determinati. Metoda se numeste "lineara" intrucat functia,
care defineste modelul matematic de aproximare, este de gradul intai in coeficienti. Pentru a
ilustra procesul de aproximare prin aceasta metoda, este suficient a
arata modul in care este rezolvata ecuatia de gradul intai
, in care cei doi coeficienti urmeaza a fi
determinati. Metoda se numeste "lineara" intrucat functia,
care defineste modelul matematic de aproximare, este de gradul intai in coeficienti. Pentru a
ilustra procesul de aproximare prin aceasta metoda, este suficient a
arata modul in care este rezolvata ecuatia de gradul intai 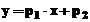 , in necunoscutele
, in necunoscutele 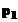 si
si 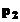 , daca se considera n puncte cunoscute. Daca se scriu cele n ecuatii corespunzatoare datelor cunoscute, se
obtine un sistem de n ecuatii
care urmeaza a fi rezolvat:
, daca se considera n puncte cunoscute. Daca se scriu cele n ecuatii corespunzatoare datelor cunoscute, se
obtine un sistem de n ecuatii
care urmeaza a fi rezolvat: 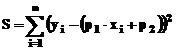 . Diferentiind in raport cu cele doua necunoscute
. Diferentiind in raport cu cele doua necunoscute 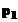 si
si 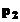 , intrucat metoda minimizeaza
suma patratelor reziduurilor, se obtin doua expresii
suplimentare:
, intrucat metoda minimizeaza
suma patratelor reziduurilor, se obtin doua expresii
suplimentare:
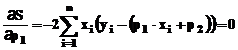
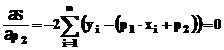
Aceste
ecuatii sunt rezolvabile in raport cu cele doua necunoscute:
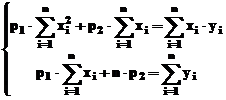 ale carui
solutii sunt:
ale carui
solutii sunt:
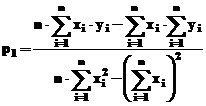 respectiv
respectiv 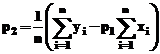 .
.
Ceea
ce se poate constata usor, este faptul ca utilizarea acestei metode
pentru aproximare si ajustare, inseamna doar calcule algebrice
simple.
In
forma matriceala, metoda lineara a celor mai mici patrate este
data de formula:
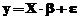
unde:
-y este un vector coloana (n linii ), al raspunsurilor;
-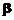 este un vector coloana (m linii), al coeficientilor;
este un vector coloana (m linii), al coeficientilor;
-X este o matrice nxm, a valorilor previzionate;
-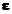 este vectorul coloana (n linii ), al erorilor.
este vectorul coloana (n linii ), al erorilor.
Pentru un polinom de gradul
intai, cele n ecuatii cu
doua necunoscute, exprimate in
functie de y, X si 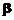 sunt:
sunt:
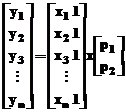
Solutia
problemei, data prin metoda celor mai mici patrate, este un vector b, care contine vectorul
coeficientilor 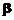 . Ecuatiile generalizate atasate acestui sistem
sunt reprezentate prin:
. Ecuatiile generalizate atasate acestui sistem
sunt reprezentate prin:
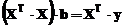 ,
,
cu solutia
generalizata:
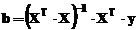
in care, XT reprezinta transpusa matricei X.
Aceasta ecuatie poate
fi rezolvata folosind operatorul ""
(impartire la stanga), respectiv, folosind factorizarea QR.
Solutia de raspuns,
previzionata, 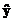 , se determina cu relatia:
, se determina cu relatia:
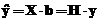 ,
,
unde:
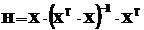
In aceste conditii,
reziduurile sunt date de relatia:
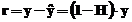
Metoda ponderata, a celor
mai mici patrate
In
evaluarea rezultatelor experimentale, a masuratorilor, in general, se
presupune ca, datele obtinute au aceeasi "calitate", deci
si varianta este constanta.
Daca aceasta presupunere nu este valida, fiind prezente
perturbatii evidente, atunci procesul de ajustare a reprezentarilor
grafice ale datelor obtinute, este "perturbat" si contine erori.
In consecinta, pentru cresterea calitatii aproximarii,
se poate folosi metoda, ponderata, a
celor mai mici patrate, metoda care introduce un factor de
pondere. Aceasta metoda minimizeaza eroarea estimata
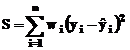
in care, 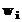 reprezinta
ponderea reziduala. Aceasta marime arata magnitudinea
influentei pe care o are fiecare raspuns in evaluarea finala a
parametrului masurat. Ponderarea este recomandata acolo unde se
cunosc marimile ponderilor, sau acolo unde este justificata o
anumita comportare a acestora.
reprezinta
ponderea reziduala. Aceasta marime arata magnitudinea
influentei pe care o are fiecare raspuns in evaluarea finala a
parametrului masurat. Ponderarea este recomandata acolo unde se
cunosc marimile ponderilor, sau acolo unde este justificata o
anumita comportare a acestora.
Ponderile
modifica expresia vectorului b,
astfel:
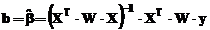 ,
,
unde, W, este dat de elementele de pe diagonala principala a
matricei ponderilor w.
Ponderile
utilizate trebuie sa transforme varianta raspunsurilor in valori
constante. Daca este cunoscuta varianta datelor, ponderea este
data prin:
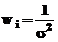
in timp ce, daca nu se
cunoaste varianta, ponderile se vor aproxima cu relatia:
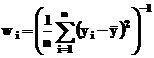
Aceasta relatie este
acoperitoare pentru calculul ponderilor, daca setul de date contine
valori identice (repetitii). In acest caz, n reprezinta numarul de replici identice.
Metoda robusta, a celor
mai mici patrate
Metoda
celor mai mici patrate, in general, este sensibila la valorile "iesite" din setul de valori,
adica din modul in care evolueaza acest set de date. Minimizarea
influentei iesirilor este
realizabila prin metoda,
robusta, a celor mai mici patrate. Aceasta metoda este
disponibila in doua variante:
- Metoda
reziduurilor absolute (LAR=Least
Absolute Residuals)-aceasta metoda aproximeaza setul de
valori printr-o curba care minimizeaza diferenta
absoluta a reziduurilor, in raport cu diferenta patratelor
acestora. Din acest motiv, valorile extreme au o influenta
redusa.
- Metoda
ponderilor bipatrate -Aceasta varianta a metodei
minimizeaza suma patratelor ponderilor, in care ponderea
reprezinta "distanta" lacare se gaseste fiecare punct
fata de linia de aproximare. Astfel, punctele apropiate de
curba au o pondere ridicata, iar punctele "indepartate" de
curba, dau ponderi reduse (valori apropiate de zero).
Metoda
ponderilor bipatrate este preferata metodei reziduurilor absolute,
intrucat prima metoda minimizeaza efectul valorilor extreme.
Metoda,
robusta, a celor mai mici patrate, varianta ponderilor bipatrate
utilizeaza un algoritm de ponderare, si urmareste
urmatoarea procedura:
- Aproximeaza modelul prin ponderarea celor mai
mici patrate;
- Se determina reziduurile
ajustate, si se "actualizeaza". Reziduurile ajustate, se determina cu relatia:
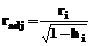
in care ri este reziduul
patratic uzual, iar hi este
"rotunjirea" care ajusteaza reziduurile prin lipsa. "Actualizarea" se
realizeaza prin:
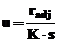 ,
,
unde K este o constanta de reglaj K=4.685. si s este varianta robusta
data prin relatia:
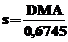
in care DMA reprezinta deviatia medie absoluta a
reziduurilor;
- Calculul ponderilor robuste ca functie de u. Ponderile bipatrate sunt
date prin:
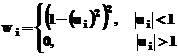
- Daca aproximarea este convergenta atunci
rezultatul este corect, altfel, se trece la o noua iteratie a ajustarii,
prin reintoarcerea la primul pas al procedurii.
Metoda nelineara a celor
mai mici patrate
MATLAB
dispune de o varianta a metodei celor mai mici patrate care
utilizeaza o formulare neliniara pentru aproximarea datelor. Un model
nelinear este definit printr-o ecuatie neliniara in coeficienti,
sau o combinatie liniara si neliniara (aproximarea Gauss
sau aproximarea rationala de polinoame).
In
forma matriceala, modelul neliniar este dat de formula:
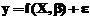
unde
- y este vectorul
coloana al raspunsurilor (n
linii);
- f este o
functie de
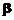 si X;
si X;
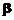 este vectorul
coloana al coeficientilor (m
linii);
este vectorul
coloana al coeficientilor (m
linii);- X este
matricea proiectata a modelului (n
linii, m coloane );
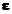 este vectorul
coloana al erorilor (n
linii).
este vectorul
coloana al erorilor (n
linii).
Modelele
nelineare sunt, in general, mai dificil de ajustat decat modelele lineare,
intrucat coeficientii nu pot fi estimati prin metode matriciale
simple. De aceea, abordarea tehnicilor iterative trebuie sa adopte
urmatoarele etape:
- Startul cu o estimare initiala pentru
fiecare coeficient;
- Se realizeaza ajustarea pentru
coeficientii determinati. Raspunsul aproximat este dat de
relatia:

care
implica si calculul Jacobianului
functiei 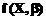 (Jacobianul este
definit prin derivatele partiale ale matricei in raport cu
coeficientii );
(Jacobianul este
definit prin derivatele partiale ale matricei in raport cu
coeficientii );
- Ajustarea coeficientilor si evaluarea
aproximarii (in MATLAB sunt disponibili algoritmii: a)-Trust region; b)-Levenberg-Marquardt; c)-Gauss-Newton);
- Iterarea procesului, prin saltul la pasul 2., atata
timp cat nu este realizata convergenta aproximarii.
Datorita
naturii procesului de aproximare in sine, nici un algoritm nu este perfect
pentru modelul neliniar al metodei celor mai mici patrate. Din acest
motiv, atunci cand rezultatele obtinute nu sunt cele asteptate, sau
apropiate de cele asteptate, se ia decizia schimbarii metodei
implicite de aproximare, mai ales ca metodele neliniare sunt sensibile la
punctul de start al aproximarii.
INTERPOLAREA DATELOR,
folosind matlab
Interpolarea,
asa cum s-a afirmat si anterior, in cadrul acestui capitol, este un
proces prin care se realizeaza estimarea numerica a valorilor
intermediare prin care face conexiunea intre punctele corespunzatoare datelor
cunoscute. Interpolarea are aplicatii deosebit de importante in procesarea
imaginilor si a semnalelor (achizitiei de date). Se disting :metode
de interpolare lineara, bi-dimensionala, Spline, Fourier,
bi-lineara, bi-armonica, bi-cubica, multi-dimensionala,
prin triangularizare.
In
figurile urmatoare se poate observa, in principiu, efectul procesului de
interpolare, pentru un set de semnale masurate.
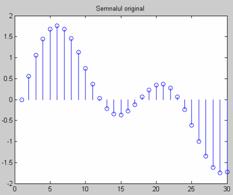
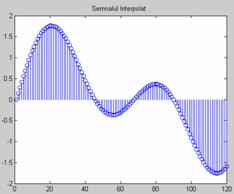
Semnalul original Semnalul interpolat
Fie 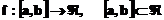 . Se pune problema determinarii unei
functii F, care sa aproximeze functia f in intervalul [a,b]. Se recurge la aceasta
aproximare in doua cazuri:
. Se pune problema determinarii unei
functii F, care sa aproximeze functia f in intervalul [a,b]. Se recurge la aceasta
aproximare in doua cazuri:
-cand nu se cunoaste expresia
analitica a lui f, dar se cunosc valorile sale
intr-un numar finit de puncte;
-cand expresia analitica a lui f este destul de complicata si
cu ajutorul acesteia calculele sunt destul de dificile.
Pentru evaluarea lui f(x)
se cauta o alta functie F(x) relativ simpla astfel ca
pentru orice valoare a lui x valoarea lui f(x) se alege dintr-o
anumita clasa de functii, de exemplu din clasa polinoamelor de
grad n
sau mai mic, atunci trebuie ca F(x) sa ia aceeasi valoare
cu f(x)
pentru anumite valori ale lui x. Aceste valori ale lui x
sunt adesea numite puncte de interpolare.
De asemenea se poate cere ca anumite derivate ale lui F(x) sa ia aceleasi
valori cu valorile derivatelor corespunzatoare ale lui f(x)
in anumite puncte de interpolare. Se poate arata ca daca F(x)
este suma a n+1 termeni ai seriei Taylor pentru f(x) in punctul x=a, atunci F(x) poate fi considerat
ca un polinom de interpolare pentru f(x) de grad n sau mai mic, deoarece 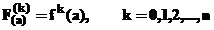 .
.
Modele parametrice
In
MATLAB sunt disponibile cateva modele parametrice consacrate, pentru
interpolarea si aproximarea datelor:
- Functii exponentiale
Exista
doua variante ale acestui model parametric:
- Modelul exponential cu un termen:
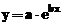 ;
;
- Modelul exponential cu doi termeni:
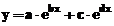 ;
;
Functiile
exponentiale sunt utilizate atunci cand rata modificarii unei
marimi este proportionala cu dimensiunea initiala a
acestei marimi. In functie de semnul exponentului, y este o functie
descrescatoare (exponent negativ), sau o functie crescatoare
(exponent pozitiv);
- Serii Fourier
Sunt modele reprezentate prin sume de
functii trigonometrice simple:
- Modelul Gauss
Acest model este utilizat pentru
aproximarea valorilor "de varf". De exemplu, aproximarea liniei spectrale de
emisie pentru analiza concentratiei chimice, poate fi descrisa
printr-o aproximare Gauss. Modelul matematic asociat, este dat de ecuatia:
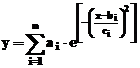 ,
,
unde a este amplitudinea, b este centroidul, c este dat de latimea relativa a "varfului", iar n este numarul de "varfuri" ce
urmeaza a fi aproximate ( 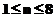 )
)
- Modelul polinomial
Ecuatia caracteristica acestui
model este: 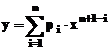 , in care (n+1)
reprezinta ordinul polinomului, (n) reprezinta gradul polinomului. Ordinul polinomului da numarul de
coeficienti ce urmeaza a fi aproximati, iar gradul polinomului
arata puterea variabilei previzionate. Modelele polinomiale sunt folosite
atunci cand sunt necesare aproximari empirice simple. Acestea pot fi
utilizate in cazul interpolarilor sau extrapolarilor seturilor de
date.
, in care (n+1)
reprezinta ordinul polinomului, (n) reprezinta gradul polinomului. Ordinul polinomului da numarul de
coeficienti ce urmeaza a fi aproximati, iar gradul polinomului
arata puterea variabilei previzionate. Modelele polinomiale sunt folosite
atunci cand sunt necesare aproximari empirice simple. Acestea pot fi
utilizate in cazul interpolarilor sau extrapolarilor seturilor de
date.
- Serii de puteri
Sunt disponibile doua variante ale
acestui model, ca si in cazul modelului functiilor exponentiale:
- Modelul seriilor de puteri cu un termen:
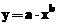 ;
;
- Modelul exponential cu doi termeni:
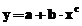 ;
;
- Expresii rationale
Expresiile rationale sunt date de
modele matematice descrise de ecuatii de forma: 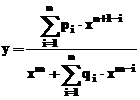 , in care gradul numaratorului,
, in care gradul numaratorului,  , respectiv gradul numitorului
, respectiv gradul numitorului 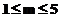 , iar coeficientul lui
, iar coeficientul lui 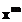 este, intotdeauna,
unu. Modelele rationale sunt avantajoase datorita
flexibilitatii mari in cazul structurilor de date complicate, dar
prezinta dezavantajul instabilitatii accentuate atunci cand
numitorul ia valori aproape de zero.
este, intotdeauna,
unu. Modelele rationale sunt avantajoase datorita
flexibilitatii mari in cazul structurilor de date complicate, dar
prezinta dezavantajul instabilitatii accentuate atunci cand
numitorul ia valori aproape de zero.
- Sume de sinus
Modelul matematic este dat de
relatia: 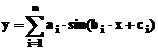 , in care a este
amplitudinea, b, este
frecventa, iar c este constanta
de faza pentru fiecare termen al sumei de sinusi (
, in care a este
amplitudinea, b, este
frecventa, iar c este constanta
de faza pentru fiecare termen al sumei de sinusi (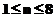 ).
).
- Distributia Weibull
Acest model este utilizat in analiza
datelor statistice legate de fiabilitatea si de durata de viata
a produselor. Expresia matematica este: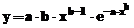 , in care a este
parametrul de scara iar b este
factorul de forma. Modelul matematic poate contine un parametru
suplimentar c, centroidul, atunci
cand x este inlocuit cu x-c. De remarcat ca
distributia Weibull nu aproximeaza datele unui set de date, ci
aproximeaza curbele astfel incat acestea sa aiba forma apropiata
de forma distributiei Weibull.
, in care a este
parametrul de scara iar b este
factorul de forma. Modelul matematic poate contine un parametru
suplimentar c, centroidul, atunci
cand x este inlocuit cu x-c. De remarcat ca
distributia Weibull nu aproximeaza datele unui set de date, ci
aproximeaza curbele astfel incat acestea sa aiba forma apropiata
de forma distributiei Weibull.
- Modele utilizator
Modelele matematice, definite implicit, nu
sunt cele mai bune modele in toate cazurile. Din acest motiv, uneori, este
necesar a se defini ecuatii specifice unei anumite aplicatii. Aceste
ecuatii sunt avantajoase intrucat coeficientii punctului de start al
iteratiei se aleg aleatoriu din intervalul [0,1], iar pentru calculul Jacobianului se foloseste
diferentiala totala.
Functiile
MATLAB pentru interpolarea datelor
In tabelul
urmator sunt prezentate selectiv functiile MATLAB, utilizate pentru
interpolarea datelor:
|
Functia MATLAB
|
Descriere
|
|
|
|
table1
|
- cautare in tabele si interpolare
lineara in tabele uni-dimensionale
- In versiunile superioare ale MATLAB este inlocuita cu
functia interp1
|
|
table2
|
- cautare in tabele si interpolare
lineara in tabele bi-dimensionale
- In versiunile superioare ale MATLAB este inlocuita cu
functia interp2
|
|
spline(x,y,xx)
spline(x,y)
|
interpolare spline
cubica in tabele uni-dimensionale
determina componentele
polinomiale ale curbei spline de aproximare, pentru utilizarea cu functia
MATLAB ppval()
|
|
interpft(x,n)
interpft(x,n,dim)
|
- interpoleaza prin metoda Transormatei
Fourier rapide (fft)
|
|
|
|
interp1(x,Y,xi)
interp1(Y,xi)
interp1(x,Y,xi,metoda)
|
- interpoleaza linear, spline sau cubic in
tabele uni-dimensionale
- cautare in tabele uni-dimensionale
|
|
interp2(X,Y,Z,XI,YI)
interp2(Z,XI,YI)
interp2(X,Y,Z,XI,YI,metoda)
|
|
|
interp3(X,Y,Z,V,XI,YI,ZI)
interp3(,metoda)
|
- interpoleaza date in trei dimensiuni
- cautare in tabele
|
|
interpn(X1,X2,X3,V,Y1,Y2,Y3,..)
interpn(V,Y1,Y2,Y3,)
interpn(,metoda)
|
- interpolare lineara, spline,
spline-cubica a datelor multi-dimensionale
- cautare in tabele
|
|
griddata(x,y,z,XI,YI)
griddata(x,y,z,xi,yi)
griddata(,metoda)
|
- aproximeaza si
ajusteaza o suprafata z=f(x,y) la datele vectorului tridimensional (x,y,z),
neuniform spatiat, prin interpolarea la punctele specificate (XI,YI), cu
conditia ca suprafata sa treaca, intotdeauna, prin punctele
date.
|
|
griddata3(x,y,z,v,xi,yi,zi)
griddata3(,'metoda')
|
- aproximeaza si ajusteaza o
suprafata w=f(x,y,z) data de vectorul spatial neuniform
(x,y,z,v), prin interpolare in punctele specificate (xi,yi,zi)
|
|
interpstreamspeed(X,Y,Z,U,V,W,vertices)
|
- interpoleaza liniile de camp prin
vertex-uri, pe baza datelor specificate in vectorii U,V,W, ale caror
coordonate sunt date de matricile X,Y,Z.
|
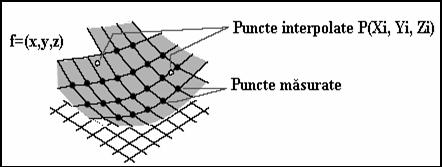
Interpolarea lineara
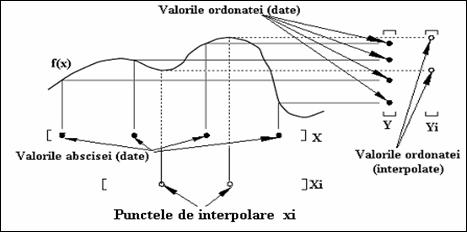 Interpolarea este o operatie
similara "cautarii in tabele". Functia MATLAB
Interpolarea este o operatie
similara "cautarii in tabele". Functia MATLAB interp1() interpoleaza intre punctele
date, gasind valorile unei functii uni- dimensionale f(x)
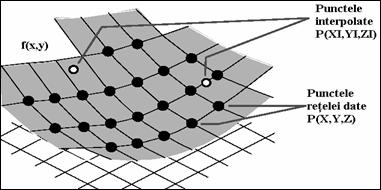
pe baza acestor puncte. In figura de mai jos este prezentata schematic relatia dintre vectorii x,
Y, xi, yi.
Prin interpolarea cu
functia MATLAB interp1 se cauta elementele xi in vectorul x,
si, pe baza locatiilor acestora, se returneaza valorile yi
interpolate printre elementele vectorului y.
In
MATLAB 6 sunt disponibile mai multe variante ale functiei interp1():
yi = interp1(x,Y,xi)
yi = interp1(Y,xi)
yi = interp1(x,Y,xi,metoda)
yi = interp1(x,Y,xi,metoda,extrapolata)
Toate variantele
de apelare a functiei interp1()
returneaza un vector yi continand
elementele corespunzatoare
elementelor vectorului xi determinate
prin interpolarea vectorilor x
si Y. Vectorul x specifica punctele in care sunt
date valorile Y. Daca Y este o matrice, atunci interpolarea
este realizata pentru fiecare coloana a matricei Y. Pentru realizarea corecta a interpolarii este
necesara corespondenta intre dimensiunile vectorului xi si dimensiunea matricei Y (in sensul ca aceste doua
entitati sa aiba acelasi numar de linii).
Varianta yi = interp1(x,Y,xi,metoda), permite
realizarea interpolarii folosind metode alternative:
'nearest' -interpolarea prin puncte apropiate
vecine
'linear' -interpolare lineara
(implicita)
'spline' -interpolare Spline
cubica
'pchip' -interpolare cubica
Hermite( Piecewise cubic Hermite interpolation)
'cubic' -Similara
interpolarii 'pchip'
'v5cubic' -interpolare cubica, utilizata
in MATLAB 5
Daca
un element al vectorului xi se
gaseste in exteriorul intervalului cuprins de x, atunci, metoda de interpolare specificata, va fi
utilizata pentru extrapolare.
 Ex. :
Ex. :
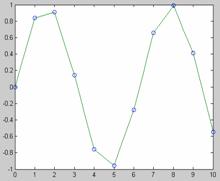
Sa se genereze o curba
sinusoidala "primara", apoi sa se interpoleze peste un
numar mai mare de abscise:
Solutie:
Varianta A
» x = 0:10;
» y = sin(x);
» xi = 0:.25:10;
» yi = interp1(x,y,xi);
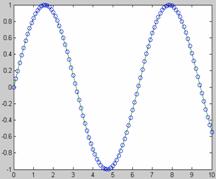 » plot(x,y,'o',xi,yi)
» plot(x,y,'o',xi,yi)
Varianta B
» x = 0:0.1 :10;
» y = sin(x);
» xi = 0:.25:10;
» yi = interp1(x,y,xi);
»
plot(x,y,'o',xi,yi)
Ex. :
Se considera doi
vectori: unul reprezentand deceniile 1 pana la 9 ale secolului trecut, cel
de-al doilea reprezentand populatia Statelor Unite ale Americii (in
milioane locuitori) pentru fiecare inceput de deceniu:
t = 1900:10:1990; p = [75.995 91.972 105.711 123.203 131.669 150.697 179.323 . 203.212 226.505 249.633];
Se cere estimarea populatiei
Statelor Unite ale Americii corespunzatoare anului 1975, apoi sa se
estimeze populatia pe fiecare an in parte incepand din 1900 si
pana in 2000, reprezentand grafic rezultatul obtinut.
Solutie:
Prin interpolare:
»populatia_in_1975=interp1(t,p,1975)
se obtine rezultatul:
»populatia_in_1975= 214.8585
Interpoland intre anii 1900 si 2000 se obtin rezultatele, respectiv, graficul evolutiei
populatiei intre anii 1900
si 2000:
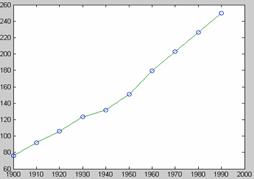 » x = 1900:2000; » y = interp1(t,p,x); » plot(t,p,'o',x,y)
» x = 1900:2000; » y = interp1(t,p,x); » plot(t,p,'o',x,y)
Interpolarea bidimensionalA
Interpolarea
bi-dimensionala se realizeaza prin functia MATLAB interp2()
care se poate apela in urmatoarele variante :
ZI =
interp2(X,Y,Z,XI,YI)
ZI =
interp2(Z,XI,YI)
ZI =
interp2(Z,de_n_ori)
ZI =
interp2(X,Y,Z,XI,YI,metoda)
Oricare dintre aceste variante returneaza o
matrice ZI care contine
elementele corespunzatoare punctelor (XI,YI)
si determinate prin interpolare in matricile X, Y si Z, (Z este definita ca functie bi-dimensionala de
elementele matricilor X si Y);
Matricile X
si Y trebuie sa fie
ordonate monoton crescator, si sa fie in acelasi format;
Matricile X
si Y definesc punctele in
care este data matricea Z.
XI si YI pot fi matrici, caz in care,
functia interp2(), determina valorile matricei Z corespunzatoare punctelor (XI(i,j), YI(i,j)).
o
Daca functia interp2 este
apelata cu varianta ZI =
interp2(Z,XI,YI), atunci se interpreteaza, automat de catre
MATLAB, ca X = 1:n si Y = 1:m, unde [n, m]=size(Z)
o
Varianta
ZI = interp2(Z,de_n_ori) specifica repetarea interpolarii
bi-dimensionale, de n ori.
o
Varianta ZI
= interp2(X,Y,Z,XI,YI,metoda)
specifica metoda
alternativa de interpolare:
'linear' -pentru
interpolare bi-lineara
'nearest' -pentru
interpolarea pe vecinatati
'spline' -pentru
interpolarea spline cubica
'cubic' -
pentru interpolarea bi-cubica
Concluzie Oricare dintre aceste variante
interpoleaza intre punctele unei retele bi-dimensionale, fiind
gasite valorile unei functii f(x,y)
care face conexiunea intre punctele intermediare.
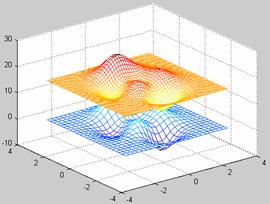
De exemplu, se cere
interpolarea, pe o retea [X,Y],
a functiei MATLAB peaks() (aceasta
functie, de doua variabile, este obtinuta prin translatarea
si scalarea distributiilor GAUSS), pe o retea [XI,YI] mai fina decat [X,Y] .
Solutia este :
» [X,Y] = meshgrid(-3:.25:3);
» Z =
peaks(X,Y);
» [XI,YI]
= meshgrid(-3:.125:3);
» ZI =
interp2(X,Y,Z,XI,YI);
»
mesh(X,Y,Z), hold, mesh(XI,YI,ZI+15)
» hold off
»axis([-3 3 -3 3 -5 20])
Interpolare tridimensionalA
Interpolarea
tridimensionala, in MATLAB, se realizeaza cu functia interp3() care se poate apela in urmatoarele
variante :
» VI = interp3(X,Y,Z,V,XI,YI,ZI)
»
VI = interp3(V,XI,YI,ZI)
»
VI = interp3(V,de_n_ori)
»
VI = interp3(,metoda)
Oricare
dintre aceste variante realizeaza interpolarea prin cautarea
valorilor matricei VI, reprezentand
valorile intermediare ale functiei tridimensionale V in punctele retelei date de matricile XI, YI si ZI. Matricile, sau vectorii, XI, YI si ZI trebuie sa
fie de aceeasi dimensiune, respectiv sa fie ordonate monoton.
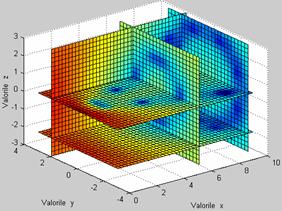
De exemplu, folosind si functia
MATLAB slice(), se interpoleaza
datele retelei tri-dimensionale [x,y,z,v] = flow(10), pentru a gasi
valorile corespunzatoare punctelor [xi,yi,zi] :
» [x,y,z,v] = flow(10);
» [xi,yi,zi] = meshgrid(.1:.25:10,
-3:.25:3, -3:.25:3);
» vi = interp3(x,y,z,v,xi,yi,zi);
» slice(xi,yi,zi,vi,[6 9.5],2,[-2 .2])
|
|
Planul de
sectionare y=[2]
|
|
Interpolarea spline, cubica
Curba spline cubica este
o curba neteda, definita de un set de polinoame de gradul trei.
Curba, « de conectare lina », dintre fiecare set de puncte este
definita printr-un polinom de gradul trei, determinat astfel incat sa
conduca la tranzitii netede de la un polinom de gradul III la altul.
Spre exemplu, trei puncte sunt conectate cu doua curbe de gradul trei,
diferite, ceea ce constituie o functie neteda intre toate cele trei
puncte.
Obs. :
De retinut : diferenta dintre metoda de interpolare lineara si interpolarea spline, care consta in aceea ca metoda spline permite « extrapolarea », adica
se pot estima valori care nu se gasesc in setul ordonat.
Interpolarea spline cubica se face in
MATLAB cu functia:
yy = spline(x,y,xx)
pp = spline(x,y)
unde:
x,y sunt vectori linie ce contin abscisele, respectiv
ordonatele punctelor;
xi este vector ce contine noua abscisa
Ex.:
Sa se determine valoarea y1 de interpolare pentru x1=2.7;
daca:
»x=[0,1,2,3,4,5] ; y=[0,20,60,68,77,100] ;
In MATLAB (considerand ca au fost deja introdusi vectorii x si y):
»y1=spline(x,y,2.7)
y1=67.4340
Ex.:
Folosind
aceiasi vectori, se cere interpolarea in punctele (1.5,2.7) respectiv in (1.2,3.4,4.5).
Cele doua valori, in care se
cere interpolarea vor fi introduse de la tastatura intre paranteze drepte,
deci ca o matrice cu o singura linie (vector linie):
»x=[0,1,2,3,4,5] ; y=[0,20,60,68,77,100] ;
»y2=spline(x,y,[1.5,2.7])
y2=42.2500 67.4340
»y3=spline(x,y,[1.2,3.4,4.5])
y3 = 28.8320 70.0480 86.6250
Ex.:
Folosind vectorii x=[0,1,2,3,4,5]
si y=[0,20,60,68,77,100]
se cere interpolarea in "n=26" puncte echidistante situate intre 0 si 5:
»xi=0:0.2:5;
» yi=spline(x,y,xi)
yi =
Columns 1 through 8
0 -1.2480 0.7360 5.3440 11.9680 20.0000 28.8320 37.8560
Columns 9 through 16
46.4640 54.0480 60.0000 63.9040 66.1120 67.1680 67.6160 68.0000
Columns 17 through 24
68.7760 70.0480 71.8320 74.1440 77.0000 80.4160 84.4080 88.9920
Columns 25 through 26
100.0000
Ex.:
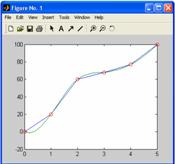 Sa
se reprezinte grafic o interpolare lineara si o interpolare spline
cubica pentru datele si rezultatele exemplului anterior.
Sa
se reprezinte grafic o interpolare lineara si o interpolare spline
cubica pentru datele si rezultatele exemplului anterior.
Pentru reprezentarea grafica se va folosi functia MATLAB plot() :
»x i=0:0.2:5;
»y i=spline(x,y,x i);
»plot(x,y,xi,yi,x,y,'o')
Ex.
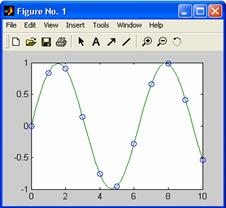 a) Fiind date 10 perechi de puncte in xOy, sa se traseze graficul
rezultat prin interpolare spline pe
o retea de patru ori mai fina (x=0:10; y=sin x)
a) Fiind date 10 perechi de puncte in xOy, sa se traseze graficul
rezultat prin interpolare spline pe
o retea de patru ori mai fina (x=0:10; y=sin x)
Solutie:
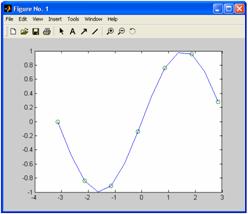
»x = 0:10; y = sin(x);
»xi = 0:0.25:10;
»yi = spline(x,y,xi);
»plot(x,y,'o',xi,yi)
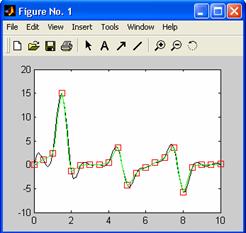
b)
Folosind,
pentru x pasul iterarii 0.5 iar functia y=tgx+sinx, sa se
reprezinte pe acelasi grafic valorile functiei (y- cu linie punctata de culoare rosie), valorile
interpolate prin metoda spline(yi-cu linie continua de
culoare magenta ) si valorile
interpolate prin metoda cubic (zi-cu linie continua de
culoare verde):
»x = 0:0.5:10; y = tan(x)+sin(x);
»xi = 0:0.125:10;
»yi = spline(x,y,xi);
»zi=interp1(x,y,xi,'cubic');
»plot(x,y,'r:',xi,yi,'m-',xi,zi,'g-')
Interpolarea multipla
Functia MATLAB
utilizata:
»interp1(x,y,xi,'regula')
in care, argumentele au semnificatia cunoscuta, iar 'regula'
este cuvantul cheie:
'linear' - interpolare lineara;
'spline' - interpolare
spline;
'cubic' - interpolare
cubica.
Toate "regulile" necesita ca
x sa fie ordonat crescator,
in plus, metoda 'cubic' impune ca
punctele x sa fie egal
distantate.
Ex.
Sa
se determine prin interpolare lineara, spline si cubica, si
apoi sa se reprezinte grafic punctele corespunzatoare valorilor -10, -9.75, -4.25, 4.15, 0.1, 6.35 daca x=-10:0.5:10, iar y=(log(abs(x+12))+2)./(exp(x)+12).
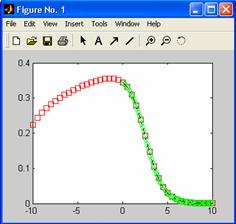 Solutie :
Solutie :
» x=-10:0.5:10;
»
y=(log(abs(x+12))+2)./(exp(x)+12);
»
xi=[-10,-9.75,-4.25,4.15,0.1,6.35];
» yi1 =
interp1(x,y,xi,'linear');
» yi2 =
interp1(x,y,xi,'spline');
» yi3 =
interp1(x,y,xi,'cubic');
»plot(x,y,'r:',xi,yi1,'m-',xi,yi2,'g-',xi,yi3,'k-.')
Regresia polinomiala
Datele
stocate in vectorul y se pot modela,
de exemplu, printr-un polinom de gradul II, ceea ce ar putea fi reprezentat
analitic prin functia: 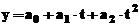 , coeficientii a0,
a1 si a2 determinandu-se dintr-un
sistem de 6 ecuatii (vectorul y are 6 elemente) cu 3
necunoscute:
, coeficientii a0,
a1 si a2 determinandu-se dintr-un
sistem de 6 ecuatii (vectorul y are 6 elemente) cu 3
necunoscute: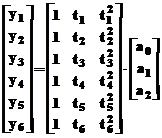 . Presupunand
ca sunt date elementele vectorului t
si ale vectorului corespondent, y,
se formeaza matricea X, a
coeficientilor sistemului, in functie de dimensiunea vectorului t, in raport de puterile intai si
a doua ale elementelor acestui vector:
. Presupunand
ca sunt date elementele vectorului t
si ale vectorului corespondent, y,
se formeaza matricea X, a
coeficientilor sistemului, in functie de dimensiunea vectorului t, in raport de puterile intai si
a doua ale elementelor acestui vector:
» t = [0, 0.3, 0.8, 1.1, 1.6, 2.3]'; y =
[0.5, 0.82, 1.14, 1.25, 1.35, 1.40]';X= [ones(size(t)) t t.^2]
X
=
1.0000 0 0
1.0000 0.3000 0.0900
1.0000 0.8000 0.6400
1.0000 1.1000 1.2100
1.0000 1.6000 2.5600
1.0000 2.3000 5.2900
Solutia
acestui sistem este:
» a=Xy
a =
0.5318
0.9191
-0.2387
»T = (0:0.1:2.5)'; Y = [ones(size(T)) T T.^2]*a; plot(T,Y,'-',t,y,'o'),
grid on
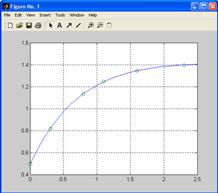 Cu aceste date se formeaza
modelul matematic polinomial de ordinul II:
Cu aceste date se formeaza
modelul matematic polinomial de ordinul II:
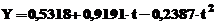 care
interpoleaza valorile vectorului y.
Reprezentand grafic acest polinom de gradul II, suprapunand cu graficul anterior, se obtine figura
alaturata.
care
interpoleaza valorile vectorului y.
Reprezentand grafic acest polinom de gradul II, suprapunand cu graficul anterior, se obtine figura
alaturata.
In
aceasta reprezentare, polinomul de interpolare este reprezentat cu "linie
continua", in timp ce valorile "date" sunt reprezentate cu simbolul grafic
"o".
Este
evident ca aceasta curba nu aproximeaza foarte exact datele
experimentale, de aceea se poate creste gradul polinomului de aproximare,
sau se pot folosi alte metode de aproximare.
Regresia exponentiala
Considerand
ca model de aproximare o functie exponentiala 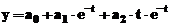 , in care parametrii ce urmeaza a fi determinati
sunt coeficientii, acestia se determina prin metoda
celor mai mici patrate. In acest sens, se construieste,
si se rezolva sistemul de ecuatii folosind matricea X, a regresiilor:
, in care parametrii ce urmeaza a fi determinati
sunt coeficientii, acestia se determina prin metoda
celor mai mici patrate. In acest sens, se construieste,
si se rezolva sistemul de ecuatii folosind matricea X, a regresiilor:
» t = [0 .3 .8 1.1 1.6 2.3]'; y = [0.5 0.82
1.14 1.25 1.35 1.40]';
» X=[ones(size(t)) exp(-t) t.*exp(-t)];
» a=Xy
a =
1.3974
-0.8988
0.4097
Modelul
matematic de aproximare se formeaza cu aceste valori determinate prin
rezolvarea sistemului de ecuatii: 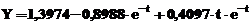 . Prin evaluarea modelului, pe un interval uniform T=0:0.1:2.5 (care include valorile
vectoruluit = [0 .3 .8 1.1 1.6 2.3]'),
si suprapunerea graficului Y(T) peste
y(t):
. Prin evaluarea modelului, pe un interval uniform T=0:0.1:2.5 (care include valorile
vectoruluit = [0 .3 .8 1.1 1.6 2.3]'),
si suprapunerea graficului Y(T) peste
y(t):
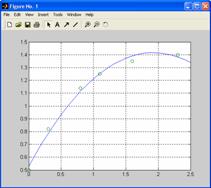 »T
= (0:0.1:2.5)';
»T
= (0:0.1:2.5)';
» Y = [ones(size(T)) exp(- T) T.*exp(-
T)]*a;
» plot(T,Y,'-',t,y,'o'), grid on
Din
aceasta figura se observa ca aproximarea cu o curba
exponentiala este mult mai "aproape" de valorile vectorului y = [0.5 0.82 1.14 1.25 1.35 1.40]'.
Regresia multipla
In cazul in
care y este o functie de mai
multe variabile independente, ecuatiile matriceale, care exprima
relatia dintre variabile, pot fi definite pentru a include si datele
aditionale. Astfel, daca se presupune ca, pentru doi parametri
diferiti, definiti vectorial, x1
= [.2 .5 .6 .8 1.0 1.1]' si x2
= [.1 .3 .4 .9 1.1 1.4]', s-au determinat experimental, statistic sau prin
alta metoda, valorile functiei, si acestea sunt cuprinse in
vectorul y = [0.17 0.26 0.28 0.23 0.27 0.24]', atunci, functia- model matematic lineara,
care ar putea exprima relatia intre parametri, este: 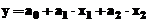 , in care ai
reprezinta parametrii lineari ce urmeaza a fi determinati.
Regresia multipla determina solutia
, in care ai
reprezinta parametrii lineari ce urmeaza a fi determinati.
Regresia multipla determina solutia 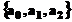 folosind metoda celor
mai mici patrate. Pentru aceasta, se construieste matricea
regresiilor, X, si se
gasesc coeficientii necunoscuti (a=[a0; a1; a2]):
folosind metoda celor
mai mici patrate. Pentru aceasta, se construieste matricea
regresiilor, X, si se
gasesc coeficientii necunoscuti (a=[a0; a1; a2]):
» x1 = [3.2 4.5 7.6 8.8 1.0 3.1]'; x2 =
[2.1 4.3 5.4 8.9 1.1 1.4]'; y = [2.5 3.3 4.5 5.2 8.9 4.7]';
» X = [ones(size(x1)) x1 x2];
» a = Xy
a =
6.4905
-1.0243
0.8208
Cu
aceste valori, funtia- model devine:
» y_model=6.4905-1.0243.*x1+0.8208.*x2
y_model =
4.9364
5.4106
3.1381
4.7818
6.3691
4.4643
Pentru
a valida acest model, se determina valoarea maxima absoluta a
deviatiei datelor modelului fata de datele observate:
» Y=X*a;
» eroarea_maxima=max(abs(Y-y))
eroarea_maxima =
2.5309
Aceasta eroare este
suficient de mare pentru a invalida modelul adoptat. Repetand
rationamentul si calculele pentru alte valori ale vectorilor x1, x2 si y se
obtin urmatoarele rezultate:
» x1 = [.2 .5 .6 .8 1.0 1.1]'; x2 = [.1 .3
.4 .9 1.1 1.4]'; y = [.17 .26 .28 .23 .27 .24]';
» X = [ones(size(x1)) x1 x2];
» a = Xy
a =
0.1018
0.4844
-0.2847
» y_model=0.1018+0.4844.*x1-0.2847.*x2
y_model =
0.1702
0.2586
0.2786
0.2331
0.2730
0.2361
» Y=X*a;
» eroarea_maxima=max(abs(Y-y))
eroarea_maxima =
0.0038
Aceasta
eroare denota faptul ca modelul poate fi validat in aceasta
varianta.
Aproximarea polinomiala de gradul n
Functia
MATLAB polyfit(), determina aproximarea
polinomiala, in sensul celor mai mici patrate, a unui set de date.
Sintaxa functiei MATLAB este:
a) » p = polyfit(x,y,n)
b) » [p,S] =
polyfit(x,y,n)
c) » [p,S,miu] =
polyfit(x,y,n)
Descriere:
Apelata in varianta a), functia p=polyfit(x,y,n), determina
coeficientii unui polinom de gradul
n, p(x), care aproximeaza
valorile (x(i)) la y(i), in sensul celor mai mici
patrate. Rezultatul, p, este un
vector linie cu n+1 coloane,
continand coeficientii polinomiali, in ordine descendenta:
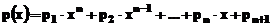
Daca
functia polyfit este
apelata in varianta b), cu
parametrii de iesire p si S, atunci, se returneaza
coeficientii polinomiali in vectorul linie p, si o structura S,
care poate fi utilizata, cu functia polyval, pentru estimarea erorilor de previzionare.
Apelarea
cu varianta c), functia polyfit, determina obtinerea
coeficientilor polinomului p,
in variabila 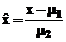 , in care
, in care 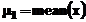 este valoarea
medie a variabilei x,
respectiv
este valoarea
medie a variabilei x,
respectiv 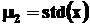 deviatia standard,
calculata cu relatia
deviatia standard,
calculata cu relatia 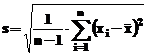 , in care
, in care 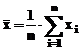 ,iar miu (
parametrul de iesire, in cazul celei de-a treia variante de apelare a
functiei polyfit), este
vectorul
,iar miu (
parametrul de iesire, in cazul celei de-a treia variante de apelare a
functiei polyfit), este
vectorul 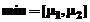 .
.
De exemplu, daca se considera setul de date
masurate x-y, si se
doreste aproximarea datelor cu o curba polinomiala de gradul III, atunci secventa MATLAB
urmatoare, determina afisarea grafica a rezultatelor
aproximarii:
» x = [1 2 3 4 5]; y = [5.5 43.1 128 290.7 498.4];
» p = polyfit(x,y,3)
p =
-0.1917 31.5821 -60.3262 35.3400
Polinomul de aproximare este: 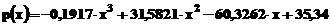 .
.
» x2 = 1:.1:5;
» y2 = polyval(p,x2);
» plot(x,y,'o',x2,y2),ylabel('Valorile determinate pentru y2' ), xlabel('Valorile x2'), grid on

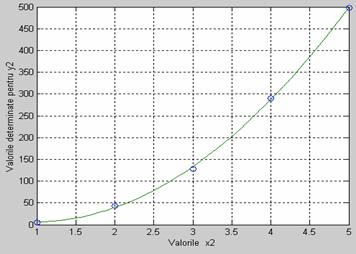
Eroarea aproximArii
Orice aproximare
numerica implica si existenta erorilor. O discutie privind erorile
de aproximare trebuie sa inceapa avand ca suport asumarea
presupunerii ca erorile apar doar in raspunsuri, niciodata in
setul de date previzionate, respectiv presupunerea ca erorile au o distributie
normala (distributie Gauss), fata de zero
(ca medie) si cu varianta constanta (de
valoare 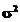 ).
).
Presupunerea ca
distributia erorilor sa fie normala, trebuie sa fie
valida intrucat aproximarea, prin orice metoda, este adecvata
doar in cazul unei distributii normale a cantitatilor
aproximate. Aceasta presupunere are la baza faptul ca
probabilitatea existentei unor valori extreme in setul de date este mica
si metoda de aproximare prin cele mai mici patrate are aplicabilitate
valida.
Media zero
a erorilor inseamna ca acestea au o aparitie pur aleatoare.
Daca media erorilor nu este zero aceasta se poate datora faptului ca
modelul ales nu este cel convenabil, sau ca erorile nu sunt aleatorii,
respectiv ca exista erori sistematice.
Varianta constanta
arata faptul ca erorile au o imprastiere constatnta.
Datele cu aceeasi varianta se numesc date de aceeasi calitate. Presupunerea ca varianta
datelor este constanta nu implica si o ponderare in sensul
aproximarii celor mai mici patrate. Aceasta se poate observa si
din procedura de aproximare, unde se presupune ca exista diferite
nivele ale ponderilor, deci calitati diferite ale datelor. Din acest
motiv se utilizeaza ponderile in metoda celor mai mici patrate, pentru
a ajusta influenta fiecarei valori din setul de date si a
corecta coeficientii aproximarii. Pentru determinarea variantei
exista doua relatii analitice de calcul:
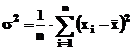 , sau
, sau 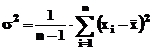 , unde
, unde 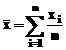 .
.
In MATLAB eroarea de
aproximare este determinata cu functia specifica erf(x). Matematic aceasta
functie este data de relatia: 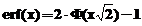 , in care
, in care 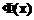 este o
functionala ce determina analitic distributia normala
standard dupa o relatie empirica:
este o
functionala ce determina analitic distributia normala
standard dupa o relatie empirica:
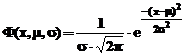
in care simbolurile utilizate au semnificatia definita in
cazul aproximarii si regresiei polinomiale, respectiv in cazul
metodei celor mai mici patrate.
Functia MATLAB erf(x) determina valoarea erorii
de aproximare a functiei model, pentru fiecare valoare a elementelor
matricei x. Aceasta eroare este
determinata prin integrala definita a distributiei normale, cand
media normata este setata la zero, iar valoarea variantei este
1/2:
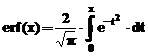
Pentru a
se demonstra limitele procedeului de aproximare, printr-o functie
polinomiala, se va prezenta un exemplu, ilustrativ. Se genereaza un
vector, uniform spatiat, x=0:0.1:2.5,
si se determina, cu functia MATLAB erf(), distributia Gauss a erorilor
» x = (0: 0.1:2.5)';
» y = erf(x);
Coeficientii
polinomului de aproximare, de gradul VI,
sunt determinati cu functia MATLAB polyfit():
»p = polyfit(x,y,6)
» p =
0.0084 -0.0983 0.4217 -0.7435 0.1471 1.1064 0.0004
Pentru a
determina cat de apropiata este ajustarea polinomiala, se va evalua polinomul p(x) in punctele vectorului x,
si se afiseaza tabelar valorile:x, y, valorile polinomului de aproximare, abaterea valorilor polinomului fata de valorile y:
» f =
polyval(p,x);
»tabel = [x y
f y-f]
tabel =
Valorile
x Valorile y Valorile f Valorile erorii
0 0 0.0004 -0.0004
0.1000 0.1125 0.1119 0.0006
0.2000 0.2227 0.2223 0.0004
0.3000 0.3286 0.3287 -0.0001
0.4000 0.4284 0.4288 -0.0004
0.5000 0.5205 0.5209 -0.0004
0.6000 0.6039 0.6041 -0.0002
0.7000 0.6778 0.6778 0.0000
0.8000 0.7421 0.7418 0.0003
0.9000 0.7969 0.7965 0.0004
1.0000 0.8427 0.8424 0.0003
1.1000 0.8802 0.8800 0.0002
1.2000 0.9103 0.9104 -0.0000
1.3000 0.9340 0.9342 -0.0002
1.4000 0.9523 0.9526 -0.0003
1.5000 0.9661 0.9664 -0.0003
1.6000 0.9763 0.9765 -0.0002
1.7000 0.9838 0.9838 0.0000
1.8000 0.9891 0.9889 0.0002
1.9000 0.9928 0.9925 0.0003
2.0000 0.9953 0.9951 0.0002
2.1000 0.9970 0.9969 0.0001
2.2000 0.9981 0.9982 -0.0001
2.3000 0.9989 0.9991 -0.0003
2.4000 0.9993 0.9995 -0.0002
2.5000 0.9996 0.9994 0.0002
Se poate
observa ca, pe acest interval, ajustarea polinomiala este relativ
corespunzatoare, dar, daca se extinde intervalul (vectorul x devine x=0:0.1:5), reprezentarea grafica arata ca aproximarea
devine neconforma, aceasta deteriorandu-se rapid:
»x = (0: 0.1:
7)';
» y = erf(x);
» f =
polyval(p,x);
»
plot(x,y,'x',x,f,'-.'),axis([0 5 0 2])
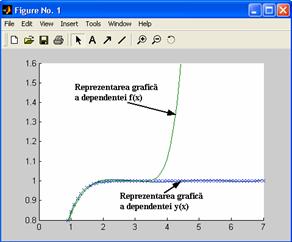
Folosind o alta facilitate
oferita de MATLAB, polytool(x,y),
care este o aproximare polinomiala de grad n interactiva, se pot observa, in urma catorva manevre simple
si intuitive, schimbarile intervenite in aproximarea prin polinoame
de diferite grade. Aceasta facilitate ofera un instrument deosebit in
analiza erorilor si curbelor de aproximare polinomiale, fiind usor de
observat care model polinomial este cel mai adecvat in aproximarea pe un anumit
interval finit.
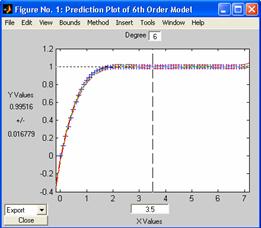
Interfata
grafica polytool realizeaza
aproximarea intre un vector coloana x
si corespondentul y al
acestuia. Interfata se activeaza prin introducerea de la
tastatura a vectorilor "tinta", x si y, respectiv a
functiei specifice polytool(x,y).
Modificarea gradului polinomului de aproximare prin regresie este posibila
in caseta Degree, in care este
necesara inscrierea gradului polinomului ( ). Valorile interpolate sunt afisate in mod curent,
pentru cele doua axe, daca vederea este bi-dimensionala,
respectiv in coordonate 3D, daca din meniul Tools, se modifica aspectul imaginii.
). Valorile interpolate sunt afisate in mod curent,
pentru cele doua axe, daca vederea este bi-dimensionala,
respectiv in coordonate 3D, daca din meniul Tools, se modifica aspectul imaginii.
Presupunand
vectorul x = (0: 0.1: 7)', si
valorile functiei y=erf(x), se
va realiza aproximarea interactiva cu instructiunile:
» x = (0: 0.1:7)';
» y = erf(x);
»
polytool(x,y,6)
obtinandu-se imaginea:
Exista
si alte functii MATLAB specifice, pentru aproximare interactiva,
precum aoctool care este
sinonima functiei polytool,
obiectivul principal al acesteia fiind, insa, analiza covariantei
modelului de aproximare.


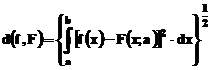
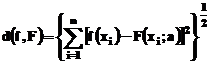

 Problema interpolarii devine neambigua daca
in locul unei functii model
Problema interpolarii devine neambigua daca
in locul unei functii model  Daca valorile tabelate
Daca valorile tabelate 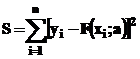
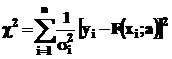
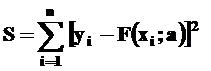
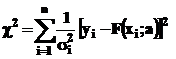
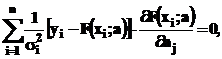
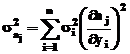
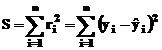 . Reziduum-ul este calculat ca diferenta dintre valoarea
"observata"
. Reziduum-ul este calculat ca diferenta dintre valoarea
"observata" 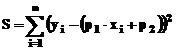 . Diferentiind in raport cu cele doua necunoscute
. Diferentiind in raport cu cele doua necunoscute 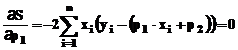
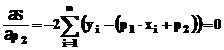
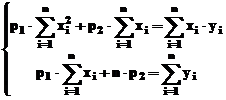 ale carui
solutii sunt:
ale carui
solutii sunt: 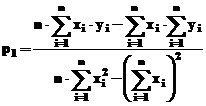 respectiv
respectiv 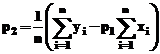 .
. 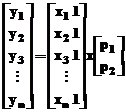
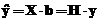 ,
,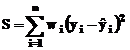
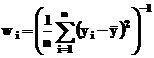
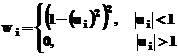



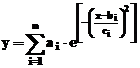 ,
, 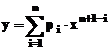 , in care (n+1)
reprezinta ordinul polinomului, (n) reprezinta gradul polinomului. Ordinul polinomului da numarul de
coeficienti ce urmeaza a fi aproximati, iar gradul polinomului
arata puterea variabilei previzionate. Modelele polinomiale sunt folosite
atunci cand sunt necesare aproximari empirice simple. Acestea pot fi
utilizate in cazul interpolarilor sau extrapolarilor seturilor de
date.
, in care (n+1)
reprezinta ordinul polinomului, (n) reprezinta gradul polinomului. Ordinul polinomului da numarul de
coeficienti ce urmeaza a fi aproximati, iar gradul polinomului
arata puterea variabilei previzionate. Modelele polinomiale sunt folosite
atunci cand sunt necesare aproximari empirice simple. Acestea pot fi
utilizate in cazul interpolarilor sau extrapolarilor seturilor de
date. 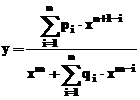 , in care gradul numaratorului,
, in care gradul numaratorului, 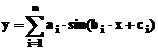 , in care a este
amplitudinea, b, este
frecventa, iar c este constanta
de faza pentru fiecare termen al sumei de sinusi (
, in care a este
amplitudinea, b, este
frecventa, iar c este constanta
de faza pentru fiecare termen al sumei de sinusi ( Interpolarea este o operatie
similara "cautarii in tabele". Functia MATLAB
Interpolarea este o operatie
similara "cautarii in tabele". Functia MATLAB  Ex. :
Ex. :




 Sa
se reprezinte grafic o interpolare lineara si o interpolare spline
cubica pentru datele si rezultatele exemplului anterior.
Sa
se reprezinte grafic o interpolare lineara si o interpolare spline
cubica pentru datele si rezultatele exemplului anterior.


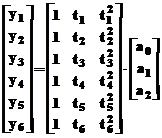 . Presupunand
ca sunt date elementele vectorului t
si ale vectorului corespondent, y,
se formeaza matricea X, a
coeficientilor sistemului, in functie de dimensiunea vectorului t, in raport de puterile intai si
a doua ale elementelor acestui vector:
. Presupunand
ca sunt date elementele vectorului t
si ale vectorului corespondent, y,
se formeaza matricea X, a
coeficientilor sistemului, in functie de dimensiunea vectorului t, in raport de puterile intai si
a doua ale elementelor acestui vector: Cu aceste date se formeaza
modelul matematic polinomial de ordinul II:
Cu aceste date se formeaza
modelul matematic polinomial de ordinul II:
 »T
= (0:0.1:2.5)';
»T
= (0:0.1:2.5)'; , in care
, in care  ,iar miu (
parametrul de iesire, in cazul celei de-a treia variante de apelare a
functiei polyfit), este
vectorul
,iar miu (
parametrul de iesire, in cazul celei de-a treia variante de apelare a
functiei polyfit), este
vectorul 

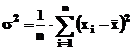 , sau
, sau 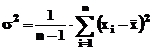 , unde
, unde 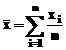 .
.