Probleme static nedeterminate - Ridicarea nedeterminarii prin metoda
integarii analitice a ecuatiei diferentiale a fibrei medii
deformate
Problema nr:1
Sa se
dimensioneze bara din figura urmatoare, stiid ca : q = 3 N/m ;
l = 0,78 m ; E = 2,1.105 N/ mm2
; 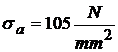 .
.
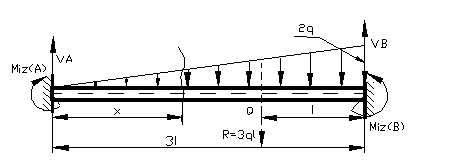
Figura 58
Scriem
conditiile de echilibru static:
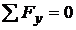 ;
; 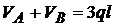 ; ecautia de verificare.
; ecautia de verificare.
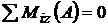 ;
; 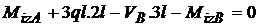 ;
; 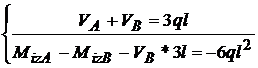
Avem 4 necunoscute
(V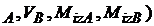 si doua ecuatii , problema este dublu static
nedeterminata. Ridicam nedeterminarea din conditia de
deformatii, avem: v
si doua ecuatii , problema este dublu static
nedeterminata. Ridicam nedeterminarea din conditia de
deformatii, avem: v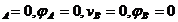 .
.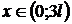 ;
; 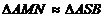 din figura 59 aplicam teorema lui Thales ( de
asemanare a triunghiurilor )
din figura 59 aplicam teorema lui Thales ( de
asemanare a triunghiurilor ) 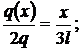 q(x)=
q(x)=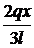
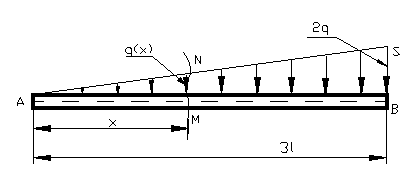
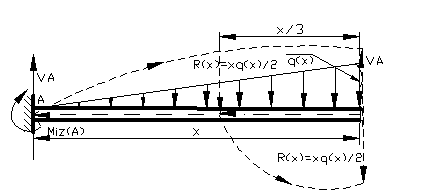
Figura 59
R(x)=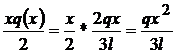 ; M
; M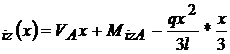 ; M
; M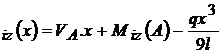
Metoda a II-a de
calcul a lui M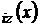 ; q(x)= ax+b este o dreapta, sarcina
distribuita. Alegem o origine 0=A si aflam pe a si b din desen ( daca se stiu
doua puncte de pe o dreapta se stie toata dreapta ) .
; q(x)= ax+b este o dreapta, sarcina
distribuita. Alegem o origine 0=A si aflam pe a si b din desen ( daca se stiu
doua puncte de pe o dreapta se stie toata dreapta ) .
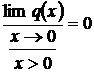 ;
; 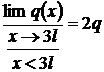 ;
; 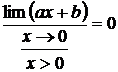 ; a*0 + b = 0 ; b = 0
; a*0 + b = 0 ; b = 0
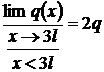 ;
; 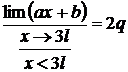 ; a 3l = 2q ; a =
; a 3l = 2q ; a = 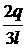 . Deci q(x) = a x +
b ; q(x) =
. Deci q(x) = a x +
b ; q(x) =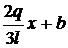
q(x) = 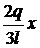 ;
; 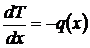 ; dT = -q(x) dx ,
; dT = -q(x) dx , 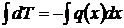 ; T(x)=-
; T(x)=-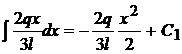
T(x)=-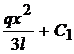 ;
; 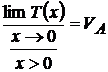 ; -
; -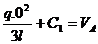 ; C
; C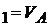 ; T(x)=V
; T(x)=V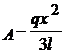
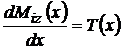 ; dM
; dM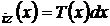 ;
; 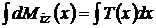 ; M
; M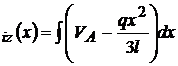
M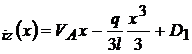 ; M
; M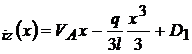 ; M
; M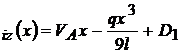
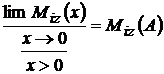 ; V
; V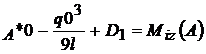 ; D
; D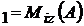 deci M
deci M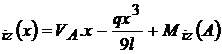
Aplicam
ecuatia fibrei medii deformate E
I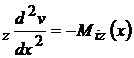 ; EI
; EI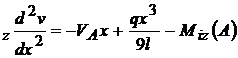
E I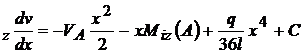 ; EI
; EI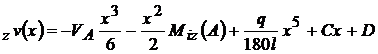
Am luat originea in
A=0 ,C=0 , D=0 , aici 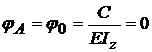 ; v
; v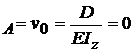 , deci,
, deci,
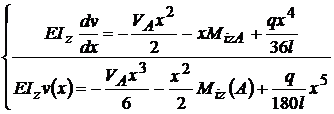 Din cele 4
conditii de reazem am folosit numai doua , avem sageata si
rotirea din A sunt zero.
Din cele 4
conditii de reazem am folosit numai doua , avem sageata si
rotirea din A sunt zero. 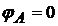 ; v
; v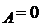 . Cele doua
ecuatii care le mai folosim pentru
a ridica nedeterminarea sunt
. Cele doua
ecuatii care le mai folosim pentru
a ridica nedeterminarea sunt 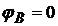 si
si
v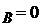 ( sageata si rotirea din incastrarea din B sunt
zero ).
( sageata si rotirea din incastrarea din B sunt
zero ).
0=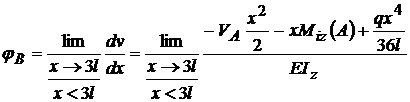 ; -V
; -V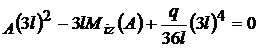
- 4,5 V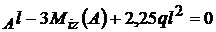 ;
;
-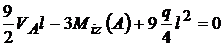
si a patra
ecuatie o obtinem din : v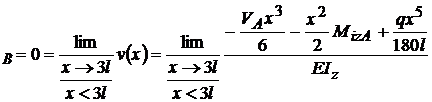
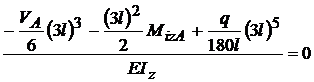 ;
; 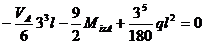
-4,5 V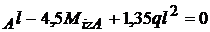
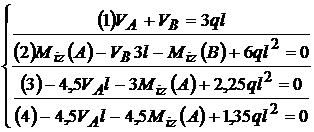
Din 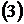 si
si 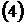 rezolvam si
aflam pe V
rezolvam si
aflam pe V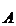 si M
si M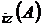
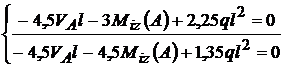
-4,5V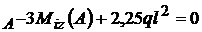
4,5 V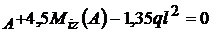
rezulta : 1,5 M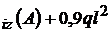 ; M
; M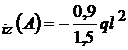 ; M
; M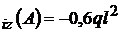
-4,5 V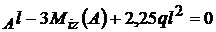 ; -4,5 V
; -4,5 V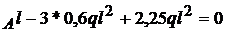 ; 4,5V
; 4,5V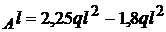
V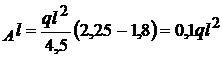 Din (1) V
Din (1) V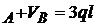 ; 0,1 ql + V
; 0,1 ql + V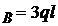 ; V
; V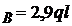
Din (2) M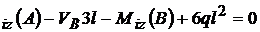 ;
;
-0,6ql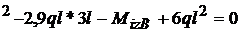
M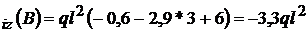 ; M
; M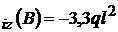 V
V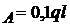
M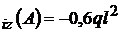 V
V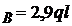
Deci , daca
s-au obtinut M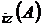 si M
si M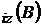 , negative le
schimbam sensul pentru ca initial l-am pus la intamplare.
, negative le
schimbam sensul pentru ca initial l-am pus la intamplare.
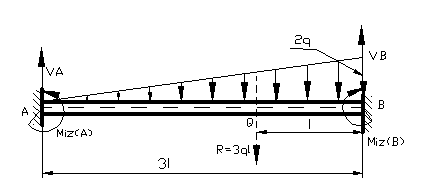
Figura 60
Ne verificam
daca am calculat corect din 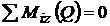
0,1 ql *2l -0,6 ql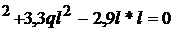 ; ql
; ql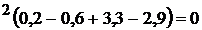 ; ql
; ql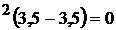 ; 0 = 0
verifica.
; 0 = 0
verifica.
Daca intr-un punct nu verifica , rezulta ca nu s-au
calculat corect, s-a gresit la calcul . Aceasta metoda
analitica se foloseste cand avem cel
mult doua regiuni pentru ca rezulta un calcul mai greoi.
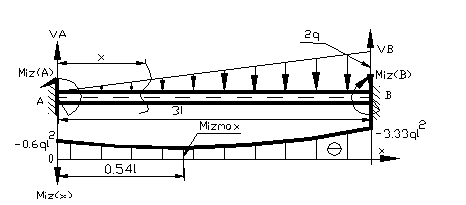
Figura 61
M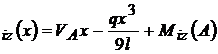 unde V
unde V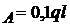 ; M
; M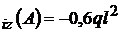 se iau sensurile initiale.
se iau sensurile initiale.
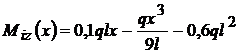 ;
; 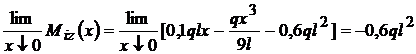 ;
;
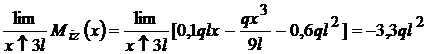 ;
; 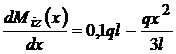 ;
; 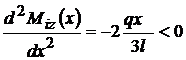 ;
;
concava . 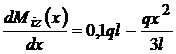 = 0 ;
= 0 ; 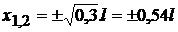 ; x = 0,54 l
; x = 0,54 l 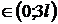
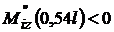 , deci x = 0,54 l este un punct de maxim.
, deci x = 0,54 l este un punct de maxim.
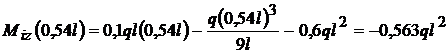 ;
;
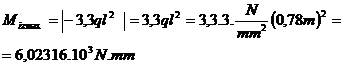
Dimensionam cu
relatia: 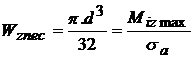 ;
; 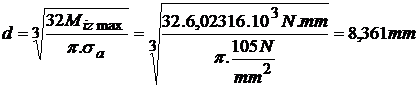 ;
;
d = 9 mm.


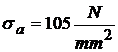 .
.
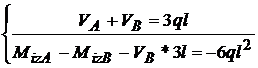
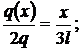 q(x)=
q(x)=

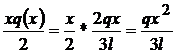 ; M
; M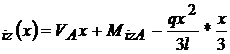 ; M
; M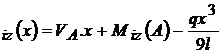
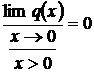
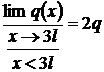 ;
; 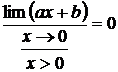 ; a*0 + b = 0 ; b = 0
; a*0 + b = 0 ; b = 0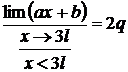 ; a 3l = 2q ; a =
; a 3l = 2q ; a = 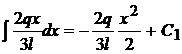
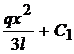 ;
; 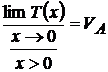 ; -
; -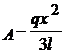
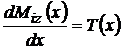 ; dM
; dM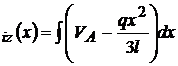
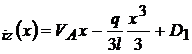 ; M
; M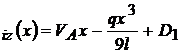
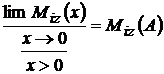 ; V
; V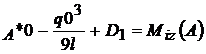 ; D
; D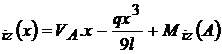
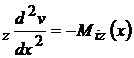 ; EI
; EI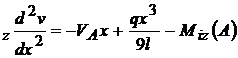
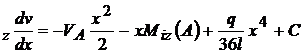 ; EI
; EI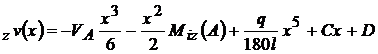
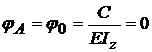 ; v
; v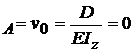 , deci,
, deci,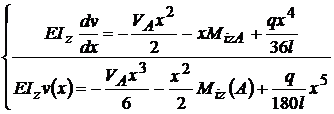 Din cele 4
conditii de reazem am folosit numai doua , avem sageata si
rotirea din A sunt zero.
Din cele 4
conditii de reazem am folosit numai doua , avem sageata si
rotirea din A sunt zero. 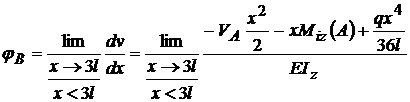 ; -V
; -V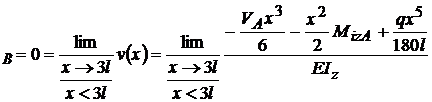
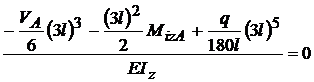 ;
; 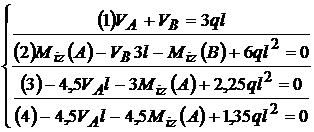
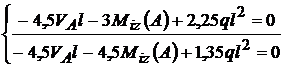
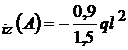 ; M
; M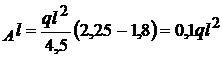 Din (1) V
Din (1) V

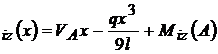 unde V
unde V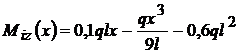 ;
; 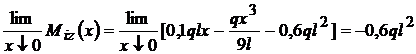 ;
;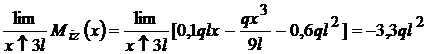 ;
; 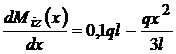 ;
; 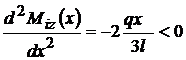 ;
;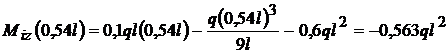 ;
; 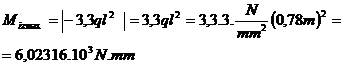
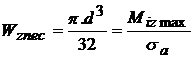 ;
; 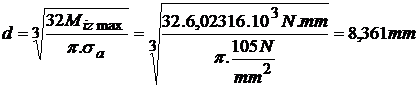 ;
;