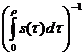Semigrupuri uniform continue

Semigrupuri uniform continue

In aceasta sectiune vom introduce notiunea de semigrup uniform continuu. Vom arata ca unicele semigrupuri uniform continue sunt cele generate de operatori liniari marginiti.

Fie X un spatiu Banach real sau complex.

Definitia I.2.1. Semigrupul S=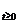 se zice uniform continuu daca

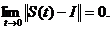
Remarca I.2.1. Orice semigrup uniform continuu este de clasa .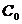

Exemplul I.2.1. Daca A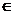 B(X) atunci 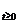este semigrup uniform continuu.

Vom demonstra in cele ce urmeaza , ca unicele semigrupuri uniform continue , sunt cele prezentate in exemplul anterior.

Teorema I.2.1. ( de caracterizare a semigrupurilor uniform continue Un semigrup S=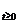 este uniform continuu daca si numai daca generatorul sau infinitezimal

A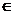 B(X).

Demonstratie. Necesitatea. Din 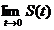= I, deducem ca

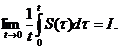
Rezulta ca exista 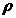> 0 astfel incat

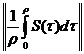< 1.

Obtinem astfel ca exista

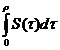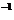
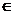() B(X).

In  plus , observam ca pentru orice y 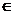X.

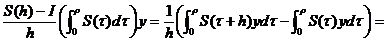
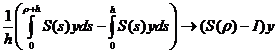= , pentru h .

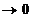De aici deducem ca

 

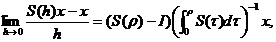
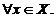
Din relatia de mai sus deducem ca D(A)=X  si

A= ( S(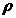)-I )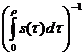 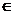B ( X ).

Suficienta. Daca A este marginit, tinand cont ca A este generatorul infinitezimal al

C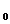- semigrupului 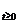, din teorema de unicitate a generarii , rezulta ca

S(t) ,  ,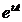

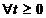deci S este un semigrup uniform continuu.

Corolarul I.2.1. Un semigrup S= 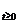este uniform continuu daca si numai daca exista un operator A 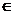B(X) astfel incat

S(t) 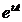, .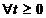
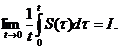
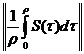
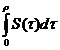