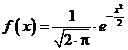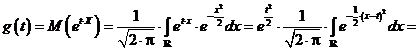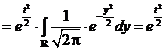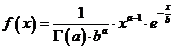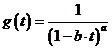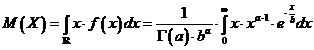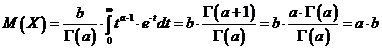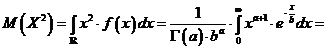| Administratie | Alimentatie | Arta cultura | Asistenta sociala | Astronomie |
| Biologie | Chimie | Comunicare | Constructii | Cosmetica |
| Desen | Diverse | Drept | Economie | Engleza |
| Filozofie | Fizica | Franceza | Geografie | Germana |
| Informatica | Istorie | Latina | Management | Marketing |
| Matematica | Mecanica | Medicina | Pedagogie | Psihologie |
| Romana | Stiinte politice | Transporturi | Turism |
- Administratie
- Alimentatie
- Arta cultura
- Asistenta sociala
- Astronomie
- Biologie
- Chimie
- Comunicare
- Constructii
- Cosmetica
- Desen
- Diverse
- Drept
- Economie
- Engleza
- Filozofie
- Fizica
- Franceza
- Geografie
- Germana
- Informatica
- Istorie
- Latina
- Management
- Marketing
- Matematica
- Mecanica
- Medicina
- Pedagogie
- Psihologie
- Romana
- Stiinte politice
- Transporturi
- Turism