Esti aici: Qreferat » Documente matematica

Retea planimetrica

RETEA PLANIMETRICA

In rerteaua de urmarire a comportarii constructiilor din schita urmatoare au fost efectuate masuratori de directii orizontale in doua etape t_o si t_1.

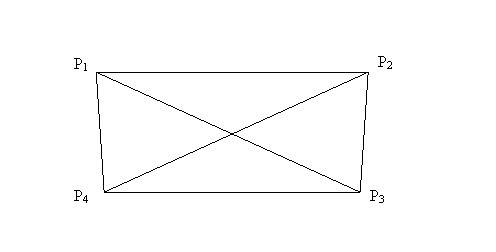
Se dau:

Coordonatele provizoriiale punctelor retelei:

Punct	X*(m)	Y*(m)
P1
P2
P3
P4

Directii masurate intre punctele de sprijin:

et₀			et₁
PS	PV	DIRECTII(G C CC)	PS	PV	DIRECTII(G C CC)
P1	P2		P1	P2
	P3			P3
	P4			P4
P2	P3		P2	P3
	P4			P4
	P1			P1
P3	P4		P3	P4
	P1			P1
	P2			P2
P4	P1		P4	P1
	P2			P2
	P3			P3

Se cere:

Sa se verifice stabilitatea punctelor retelei intre cele 2 etape.

Etape de calcul:

Calculul orientarilor provizorii si a distantelor provizorii:

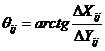
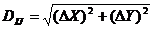
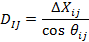
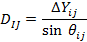
Pct	X[m]	Y [m]	θ[g c cc]	Dij [km]
P1
P2
delta
P1
P3
delta
P1
P4
delta
P2
P3
delta
P2
P4
delta
P2
P1
delta
P3
P4
delta
P3
P1
delta
P3
P2
delta
P4
P1
delta
P4
P2
delta
P4
P3
delta

Orientarea statiilor de coordonate cunoscute

Calculul unghiurilor de orientare in statie :

et0
PS	PV	Orientarea	Dir masurata	Z	Z mediu
P1	P2
	P3
	P4
P2	P3
	P4
	P1
P3	P4
	P1
	P2
P4	P1
	P2
	P3

et1
PS	PV	Orientarea	Dir masurata	Z	Z mediu
P1	P2
	P3
	P4
P2	P3
	P4
	P1
P3	P4
	P1
	P2
P4	P1
	P2
	P3

Calculul coeficientilor de directie

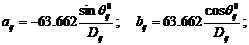
Control: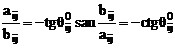

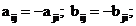
								et₀/et₁
Pct	X[m]	Y [m]	θ[g c cc]	Dij [km]	sinθ/cosθ	a [cc/mm]	b [cc/mm]	aij/bij
P1
P2
delta
P1
P3
delta
P1
P4
delta
P2
P3
delta
P2
P4
delta
P2
P1
delta
P3
P4
delta
P3
P1
delta
P3
P2
delta
P4
P1
delta
P4
P2
delta
P4
P3
delta

Forma generala a ecuatiei de corectie pentru o directie azimutala masurata intre doua puncte noi:

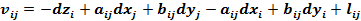
Ecuatiile de corectie pentru directiile masurate din statia P1, P2, P3 si P4

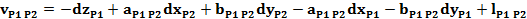
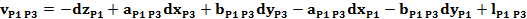
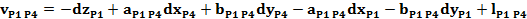
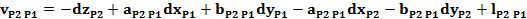
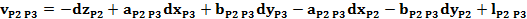
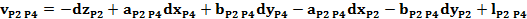
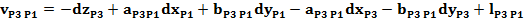
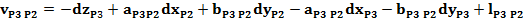
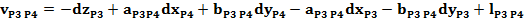
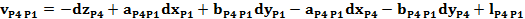
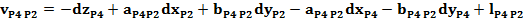
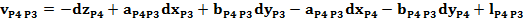
Sistemul redus al ecuatiilor de corectie:

punct

α*ij

Zsi

dXP1

dYP1

dXP2

dYP2

dXP3

dYP3

dXP4

dYP4

pij

lij [cc]

vij[cc]

- dz

dθ

θ coord

θ comp

θ+ dθ

statie

vizat

[g c cc]

necunoscute

[cc]

( g c cc)

(g c cc)

Sistemul liniar de corectii-Et 0

ECUATIE	p_i	dXP1	dYP1	dXP2	dYP2	dXP3	dYP3	dXP4	dYP4	l [ cc ]	S
V p1-p2
Vp1-p3
V p1-p4
V p2-p3
V p2-p4
V p3-p4
Vp1
Vp2
Vp3
Vp4

S

Sistemul liniar de corectii- Et₁

ECUATIE	p_i	dXP1	dYP1	dXP2	dYP2	dXP3	dYP3	dXP4	dYP4	l [ cc ]	S
V p1-p2
Vp1-p3
V p1-p4
V p2-p3
V p2-p4
V p3-p4
Vp1
Vp2
Vp3
Vp4

S

Et₁

pct

α*ij

Zsi

dXP1

dYP1

dXP2

dYP2

dXP3

dYP3

dXP4

dYP4

pij

lij [cc]

vij

- dz

dθ

θ coord

θ comp

θ+ dθ

statie

vizat

[g c cc]

necunoscute

[cc]

( g c cc)

(g c cc)

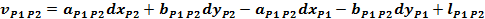
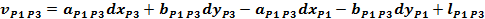
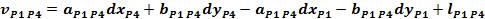
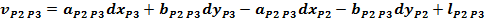
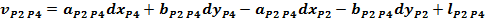
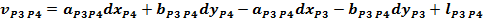
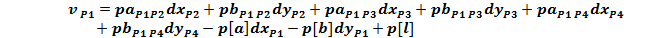
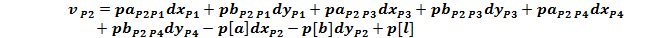
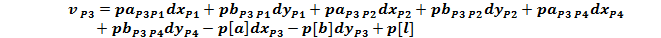
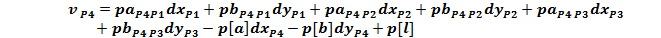
Normalizarea

V=AX+L

Et 0 si et 1






A=									l=



P=




N= AtPA

Det N=0

	X*[m]	Y*[m]	X⁰[m]	Y⁰[m]
P1
P2
P3
P4
media

Matricea ajutatoare G





G=

N	G		N+	G(G^tG)
G^t			(GtG)G^t

Control NG=0

D-1=




N+=

Et₀

X=-N⁺A^TPL

		mm
		mm
		mm
AtPl=	X=	mm
		mm
		mm
		mm
		mm

Control : G^tX=0

Coordonate compensate

Punct	X^* (m)	Y^*(m)	X(m)	Y(m)
P1
P2
P3
P4

Et₁

		mm
		mm
		mm
AtPl=	X=	mm
		mm
		mm
		mm
		mm

Control : G^tX=0

Punct	X⁰ (m)	Y⁰(m)	X(m)	Y(m)
P1					m
P2					m
P3					m
P4					m

Calculul corectiilor pentru unghiul de orientare

pentru fiecare statie se calculeaza corectia unghiului de orientare provizoriu cu relatia:

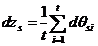, unde t este numarul de directii observate instatie;

se calculeaza corectiile v, pentru toate directiile observate se face cu relatia :

v_ij = -dz_i + d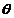_ij + l_ij;

Et0

PCT STATIE	PCT VIZAT	a* (g c cc)	z ( g c cc)	v [ cc ]	dz [ cc ]	a (g c cc)	z c ( g c cc)
P1	P2
	P3
	P4
P2	P3
	P4
	P1
P3	P4
	P1
	P2
P4	P1
	P2
	P3

Et1

PCT STATIE	PCT VIZAT	a* (g c cc)	z ( g c cc)	v [ cc ]	dz [ cc ]	a (g c cc)	z c ( g c cc)
P1	P2
	P3
	P4
P2	P3
	P4
	P1
P3	P4
	P1
	P2
P4	P1
	P2
	P3

Abaterea standard empirica

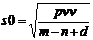
Et₀

pvv1
pvv2
pvv3
pvv4
[pvv]

PVV=		(m=12; n=12,d=4)

So=	mm

Et₁

pvv1
pvv2
pvv3
pvv4
suma

PVV=		(m=12; n=12,d=4)

So=	mm

Matricea cofactorilor Qdd = Qxx₁+Qxx₂





Q_dd=

Det Q_dd

Q_dd⁺	G(G^TG)^-1
(G^TG)^-1G^T	O

Q_dd	G
G^T	O

D-1=





Q_dd⁺

Testul Fisher

d = X1- X0 , d= vectorul discrepantelor;

s₀= (s₀₁²+s₀₂²)

s₀=88.99mm

F = d ^T Q_dd⁺ d / (h S₀²) , h = n-d

n=
d=
h=

F = valoarea calculata a testului Fisher,

h = rangul matricei Qdd;

n = dimensiunea matricei Qdd;

d = defectul de rang;





d =

d^TQ_dd⁺d =

F=
Flimita=

f = f₁+f₂ = 8 , f₁= f₂ = n-u+d = 4,unde u=numar de necunoscute u=8

F_lim = valoarea teoretica a testului Fisher ( extrasa din tabelele Fisher );

a = 5% = prag de siguranta;

F_lim = F ( f , h ) = F (0.05,8,8) = 3.438

Daca F≤F_lim = F _a_,f,hatunci (H₀) este adevarata=> E[X1]=E[X2] =>nu exista deformatii;

Daca F>F_lim = F _a,f,hatunci (H₀) este falsa=> E[X1]≠E[X2] => exista deformatii.

Localizarea punctelor deplasate:

Testul Student

s_j = s₀ Q_jj, s_j = abaterea standard empirica a fiecarui punct;

t_j = d_j/s_j , t_j = valoarea calculata a testului;

t_lim = t_f,_a, t_lim = valoarea teoretica a testului.

Nr punct	S	Sj
P1	Sx
P1	Sy
P2	Sx
P2	Sy
P3	Sx
P3	Sy
P4	Sx
P4	Sy

Nr pct	tj(mm)
P1		Punct stabil
P1		Punct stabil
P2		Punct stabil
P2		Punct stabil
P3		Punct stabil
P3		Punct stabil
P4		Punct stabil
P4		Punct stabil

t_lim= t(0.05,f) = t(0.05,8) = 2.306

Daca I t_j I ≤ t_{lim =>}(H₀) -adevarata => punctul estestabil

Daca I t_jI > t_f,1-_a= t_lim=> (H₀) -falsa=> (H₁)- adevarata (ipoteza alternativa) => punctul este miscat

Nu se poate descarca referatul
Acest document nu se poate descarca

E posibil sa te intereseze alte documente despre:

Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site.
{ Home } { Contact } { Termeni si conditii }

Documente similare:

Retea planimetrica [matematica]
Subinel, ideal si inel factor [matematica]
Inele factoriale [matematica]
Galilei [matematica]
Locuri geometrice [matematica]
Kovalevskaya Sofia [matematica]

Administratie	Alimentatie	Arta cultura	Asistenta sociala	Astronomie
Biologie	Chimie	Comunicare	Constructii	Cosmetica
Desen	Diverse	Drept	Economie	Engleza
Filozofie	Fizica	Franceza	Geografie	Germana
Informatica	Istorie	Latina	Management	Marketing
Matematica	Mecanica	Medicina	Pedagogie	Psihologie
Romana	Stiinte politice	Transporturi	Turism

Retea planimetrica

Comentarii

Caracterizari

Cauta document