Subinel, ideal si inel factor
Definitia 2.1. O
submultime nevida A' a inelului A se numeste subinel al inelului A daca operatiile algebrice de pe A induc pe A' operatii algebrice impreuna cu care A' formeaza un
inel.
Asadar, A' trebuie sa fie in particular subgrup al
grupului aditiv al lui A, ceea ce este echivalent dupa cate stim
de la grupuri cu:
1)Oricare ar fi a,b A', rezulta a b A'.
Apoi
trebuie ca operatia de inmultire pe A sa induca pe A' o operatie algebrica, ceea ce este
echivalent cu:
2)Oricare ar fi a,b A', rezulta ab A'.
Prin
urmare, conditiile 1) si 2) sunt necesare ca A' sa fie subinel al lui A. Ele sunt insa si suficiente. In
adevar, daca ele sint verificate, A' este subgrup al grupului aditiv al lui A, dupa cum rezulta din 1). Mai
ramine sa aratam ca operatia de inmultire
pe A' este asociativa, ceea ce rezulta din faptul ca operatia de
inmultire pe A este asociativa,
si ca aceasta operatie este distributiva
fata de adunare, ceea ce rezulta din faptul ca
operatia de inmultire in A este distributiva
fata de adunare. De obicei, in cazul inelelor cu unitate, se considera indeosebi
subinele care contin elementul unitate.
Propozitia
2.1. O intersectie de subinele (unitare,) ale unui inel
este un subinel (unitar).
Demonstratie. Fie i I o familie de subinele ale inelului A si B = 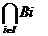 Daca a,b B, atunci a,b Bi pentru toti i I, deci a b Bi si ab Bi pentru orice i I, fiindca Bi sunt subinele. De aici rezulta ca a - b
Daca a,b B, atunci a,b Bi pentru toti i I, deci a b Bi si ab Bi pentru orice i I, fiindca Bi sunt subinele. De aici rezulta ca a - b 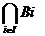 =B si ab
=B si ab 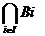 B, adica B este subinel. Este clar ca daca 1 Bi pentru toti i I, adica Bi sunt subinele unitare, atunci 1 B deci B este subinel unitar.
B, adica B este subinel. Este clar ca daca 1 Bi pentru toti i I, adica Bi sunt subinele unitare, atunci 1 B deci B este subinel unitar.
Definitia 2.3. Fie A un inel. O submultime I a lui A se numeste ideal stang (respectiv drept) sau
ideal la stanga (respectiv la
dreapta)
daca I este un subgrup al grupului aditiv al
lui A, adica:
3)Oricare ar fi a,b I, rezulta a- b I si in plus
4)Oricare ar fi a I si  A, rezulta
A, rezulta  a I (respectiv a
a I (respectiv a I).
I).
I se numeste ideal bilateral daca este ideal la stanga si la dreapta.. Din
aceasta definitie rezulta imediat ca orice ideal stang sau
drept al inelului A este un
subinel al lui A.
De
asemenea, daca inelul A este comutativ,
notiunile de ideal stang, ideal drept si bilateral coincid. De aceea,
in acest caz se foloseste denumirea de
ideal al
inelului A. In orice inel
submultimea formata din elementul nul, notata cu (0) si
intreg inelul sunt ideale bilaterale.
In continuare, daca nu vom
specifica altfel, prin inel vom intelege un inel unitar,iar prin subinel un subinel unitar. De
asemenea, toate morfismele de inele vor fi considerate unitare, daca nu se specifica altfel.
Unele dintre proprietati pot ramine
insa valabile si pentru inele,subinele si morfisme
care nu sunt unitare.
Propozitia Fie f: A →B un
morfism de inele.Atunci: i)Daca A' este un subinel in A, atunci f (A') este subinel in B. In
particular,Imf estesubinel in B. ii)Daca B' este subinel al lui
B, atunci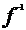 (B') este subinel in A. iii)Daca J este ideal stang (drept,
bilateral) in B, atunci
(B') este subinel in A. iii)Daca J este ideal stang (drept,
bilateral) in B, atunci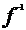 (J) este ideal stang (drept, bilateral) in A. In particular,
Ker f este ideal bilateral in A. iv)Daca in plus f este morfism
surjectiv si I este ideal stang
(drept,bilateral) in A, atunci f(I)este ideal stang(drept,bilateral) in B.
Aplicatia care asociaza unui ideal stang(drept,bilateral) J din B
idealul stang(drept,bilateral)
(J) este ideal stang (drept, bilateral) in A. In particular,
Ker f este ideal bilateral in A. iv)Daca in plus f este morfism
surjectiv si I este ideal stang
(drept,bilateral) in A, atunci f(I)este ideal stang(drept,bilateral) in B.
Aplicatia care asociaza unui ideal stang(drept,bilateral) J din B
idealul stang(drept,bilateral) 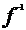 (J) din A este un izomorfism de multimi ordonate(cu incluziunea) intre idealele stangi
(drepte,bilaterale) ale lui B si idealele stangi (drepte,bilaterale) ale
lui A care contin pe Ker f. Demonstratie. i) Deoarece orice morfism de inele este
si morfism pentru grupurile aditive respective, rezulta ca f (A') este subgrup al grupului aditiv al lui B. Fie
(J) din A este un izomorfism de multimi ordonate(cu incluziunea) intre idealele stangi
(drepte,bilaterale) ale lui B si idealele stangi (drepte,bilaterale) ale
lui A care contin pe Ker f. Demonstratie. i) Deoarece orice morfism de inele este
si morfism pentru grupurile aditive respective, rezulta ca f (A') este subgrup al grupului aditiv al lui B. Fie  f (A')
.Exista atunci a,b A' astfel ca f a
f (A')
.Exista atunci a,b A' astfel ca f a  si f b Atunci, din faptul ca a,b A' si f ab f a f b), rezulta ca
si f b Atunci, din faptul ca a,b A' si f ab f a f b), rezulta ca  f (A') .Mai
observam ca elementul unitate din B apartine lui f (A'), deci
acesta este subinel in B.
f (A') .Mai
observam ca elementul unitate din B apartine lui f (A'), deci
acesta este subinel in B.
ii) Faptul ca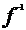 (B') este subgrup al grupului
aditiv al lui A rezulta din afirmatia corespunzatoare
demonstrata la grupuri. Este,de asemenea, evident ca 1
(B') este subgrup al grupului
aditiv al lui A rezulta din afirmatia corespunzatoare
demonstrata la grupuri. Este,de asemenea, evident ca 1 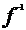 (B Fie a,b
(B Fie a,b 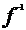 (B'), atunci f ab f a f b B', deci a,b
(B'), atunci f ab f a f b B', deci a,b 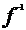 (B iii) Ca si mai sus rezulta ca
(B iii) Ca si mai sus rezulta ca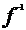 (J) este subgrup in A.
Presupunem ca J este ideal stang. Fie a
(J) este subgrup in A.
Presupunem ca J este ideal stang. Fie a 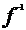 J) si
J) si  A, atunci f
A, atunci f  a f
a f  f a J. Deci
f a J. Deci  a
a 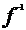 (J) .Pentru J ideal drept sau
bilateral demonstratia este analoaga. A doua afirmatie
rezulta din faptul ca (0) este ideal bilateral in B.
(J) .Pentru J ideal drept sau
bilateral demonstratia este analoaga. A doua afirmatie
rezulta din faptul ca (0) este ideal bilateral in B.
iv) Ca si in iii), demonstram
afirmatia pentru I ideal stang si ramane sa
aratam ca daca a' f I) si B avem ca
B avem ca  a' f I). Din faptul ca f este
surjectiva rezulta ca exista a I si
a' f I). Din faptul ca f este
surjectiva rezulta ca exista a I si  A astfel ca f a a' si f
A astfel ca f a a' si f 
 '. Dar I fiind ideal stang,
avem
'. Dar I fiind ideal stang,
avem  a I. Deci f
a I. Deci f  a f
a f  f a f I), prin urmare
f a f I), prin urmare  a' f I
a' f I
A doua afirmatie se demonstreaza analog cu
corolarul II,2.7. Se observa
ca aplicatia considerata este morfism de multimi ordonate
iar inversa ei este aplicatia care asociaza unui ideal I al lui A, care contine pe Ker f, pe f I) si care este de
asemenea morfism de multimi ordonate. Fie A un inel si , i I, o familie de ideale
stangi(drepte,bilaterale) in A. Atunci J = este un ideal stang (drept,bilateral) in A. In
adevar, stim ca o intersectie de subgrupuri ale unui grup
este un subgrup al acestuia, deci J este un subgrup al grupului
aditiv al lui A. Sa presupunem ca Ji sunt ideale stangi ale lui A(cazul in care Ji sunt ideale
drepte sau bilaterale se demonstreaza cu totul analog).
Fie
este un ideal stang (drept,bilateral) in A. In
adevar, stim ca o intersectie de subgrupuri ale unui grup
este un subgrup al acestuia, deci J este un subgrup al grupului
aditiv al lui A. Sa presupunem ca Ji sunt ideale stangi ale lui A(cazul in care Ji sunt ideale
drepte sau bilaterale se demonstreaza cu totul analog).
Fie  A si a
A si a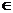 J. Atunci a
J. Atunci a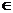 J
J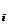 ,pentru orice i
,pentru orice i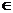 I, deci, J
I, deci, J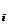 fiind ideal stang, rezulta
fiind ideal stang, rezulta  a
a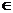 Ji pentru orice i
Ji pentru orice i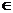 I,adica
I,adica  a
a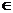
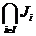 =J.
=J.
Definitia 2.5. Fie A un inel unitar si M o
submultime a lui A. Prin ideal sting (drept,
bilateral) generat de multimea M se
intelege intersectia tuturor idealelor stangi (drepte, bilaterale)
care contin multimea M. Multimea
vida genereaza idealul (0). Un ideal stang (drept, bilateral) al
inelului A se numeste de tip finit sau finit generat
daca exista o multime finita de elemente din I care
genereaza pe I. In cazul in care exista un singur element care
genereaza pe I se spune ca I este ideal sting (drept, bilateral) principal.
Propozitia 2.6. Fie A un inel, M o submultime a lui A
si I un ideal stang(bilateral) al lui A. Atunci urmatoarele
afirmatii sunt echivalente:
a) I este generat de multimea M.
b) I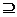 M si pentru orice ideal stang(bilateral) J in
A din J
M si pentru orice ideal stang(bilateral) J in
A din J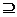 M rezulta J
M rezulta J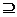 I.
I.
c) I este
multimea tuturor sumelor finite de forma
(1) x
=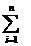
 ixi cu
ixi cu  i
i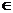 A, xi
A, xi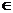 M
M
(respectiv x =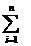

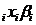 ,
, 
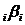 A,
A, 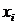
 M) pentru orice n ≥ 0 intreg.
M) pentru orice n ≥ 0 intreg.
O afirmatie analoaga este
adevarata si pentru I ideal drept. Demonstratie.
Vom demonstra afirmatia pentru cazul in care I este ideal stang, in celelalte cazuri demonstratia se face
la fel. Echivalenta dintre a) si b) este evidenta. ' '
Fie I' multimea sumelor finite
de forma (1). Atunci evident diferenta a doua sume de acest tip este
tot o suma de acest tip si inmultind la stanga o suma de
acest fel cu un element din A se obtine un alt element din
I', adica I' este ideal stang si evident contine pe M. Din b) rezulta ca I' I. Pe de alta parte, deoarece I
I. Pe de alta parte, deoarece I M si este ideal stang, rezulta
ca I
M si este ideal stang, rezulta
ca I  I',deci I= I' si s-a demonstrat astfel ca afirmatiile b) si
c) sunt echivalente.
I',deci I= I' si s-a demonstrat astfel ca afirmatiile b) si
c) sunt echivalente.
Fie I si J ideale stangi
(drepte, bilaterale) ale inelului A. Atunci prin suma acestor ideale vom intelege idealul stang
(drept, bilateral) generat de reuniunea submultimilor I si J ale lui A si se noteaza cu I+ J. Din propozitia
precedenta rezulta ca I
+ J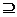 I, I + J
I, I + J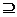 J si ca I + J este multimea elementelor
din A care se scriu sub forma x = a + b, unde a
J si ca I + J este multimea elementelor
din A care se scriu sub forma x = a + b, unde a 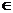 I si b
I si b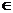 J adica I + J coincide cu subgrupul grupului aditiv
al lui A, generat de subgrupurile I si J. Daca
consideram multimea idealelor stangi (drepte, bilaterale) ale inelului
A, cu ordonarea data de incluziune (adica ordonarea indusa de
cea a multimii submultimilor lui A), din cele
demonstrate mai sus rezulta ca aceasta multime
ordonata este o latice, cele doua operatii fiind
intersectia si suma. Mai
rezulta totodata ca aceste latice sunt sublatice ale laticii
subgrupurilor grupului aditiv A. Din cele de mai
sus rezulta ca laticea idealelor stangi (respectiv drepte,
bilaterale), este completa, caci exista si suma unei
familii oarecare de ideale, stangi (drepte, bilaterale), ea este egala cu
idealul generat de reuniunea acestor ideale stangi (respectiv drepte,
bilaterale).
J adica I + J coincide cu subgrupul grupului aditiv
al lui A, generat de subgrupurile I si J. Daca
consideram multimea idealelor stangi (drepte, bilaterale) ale inelului
A, cu ordonarea data de incluziune (adica ordonarea indusa de
cea a multimii submultimilor lui A), din cele
demonstrate mai sus rezulta ca aceasta multime
ordonata este o latice, cele doua operatii fiind
intersectia si suma. Mai
rezulta totodata ca aceste latice sunt sublatice ale laticii
subgrupurilor grupului aditiv A. Din cele de mai
sus rezulta ca laticea idealelor stangi (respectiv drepte,
bilaterale), este completa, caci exista si suma unei
familii oarecare de ideale, stangi (drepte, bilaterale), ea este egala cu
idealul generat de reuniunea acestor ideale stangi (respectiv drepte,
bilaterale).
Pe multimea idealelor stangi
(drepte, bilaterale) mai introducem o operatie algebrica,
numita produsul idealelor in modul
urmator: daca I si J sunt doua
ideale stangi (drepte, bilaterale), atunci produsul lor IJ se
defineste ca fiind idealul stang (drept, bilateral) generat de
submultimea lui A formata din toate elementele
de forma x = ab, cu a 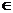 I si b
I si b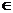 J. Din propozitia precedenta
rezulta ca IJ este
multimea tuturor elementelor x din A de forma x =
J. Din propozitia precedenta
rezulta ca IJ este
multimea tuturor elementelor x din A de forma x =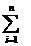 aibj,pentru n ≥ 0
aibj,pentru n ≥ 0
numar intreg intreg
convenabil si 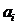
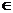 I,
I, 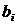
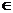 J.
J.
Se verifica imediat ca,
datorita asociativitatii inmultirii din A, inmultirea
idealelor stangi (drepte, bilaterale) este o operatie asociativa, iar
daca inelul A este comutativ, aceasta operatie este si ea
comutativa. Asadar, multimea idealelor stangi(drepte, bilaterale)
impreuna cu produsul idealelor formeaza un semigrup, care este unitar
daca inelul este unitar, elementul unitate fiind in acest caz intreg
inelul. Acest semigrup este evident comutativ daca inelul este comutativ. Daca
I si J sunt ideale stangi (drepte,
bilaterale) ale inelului A, generate respectiv de multimile M si N, atunci I +J este generat de M 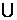 N, iar IJ este generat de multimea
produselor de forma xy, unde x M si y N, dupa cum rezulta imediat din
definitia sumei si a produsului de ideale. De aici rezulta, in
particular,ca suma si produsul a doua ideale stangi(drepte,
bilaterale) de tip finit este un ideal de tip finit. Daca A este un inel comutativ
unitar si i I este o submultime de elemente din A vom
nota cu (xi), i I sau
N, iar IJ este generat de multimea
produselor de forma xy, unde x M si y N, dupa cum rezulta imediat din
definitia sumei si a produsului de ideale. De aici rezulta, in
particular,ca suma si produsul a doua ideale stangi(drepte,
bilaterale) de tip finit este un ideal de tip finit. Daca A este un inel comutativ
unitar si i I este o submultime de elemente din A vom
nota cu (xi), i I sau 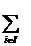 x
x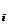 A sau inca
A sau inca 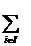 Ax
Ax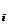 idealul
generat de aceasta multime. In particular,idealul generat de un
element x A se va nota cu (x ), xA sau Ax.
idealul
generat de aceasta multime. In particular,idealul generat de un
element x A se va nota cu (x ), xA sau Ax.
In orice inel A idealul (0) si intreg inelul
A sunt ideale principale; (0) este generat de elementul 0, iar A este generat de orice element inversabil.
Daca f : A→B este un morfism de inele, atunci
este clar ca f este injectiv daca si numai
daca Ker f = (0), dupa cum am vazut
pentru grupuri ( f
fiind si morfism de grupuri pentru structurile de grup aditiv ale lui A
si B).Morfismul f este surjectiv daca si numai daca 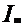 f = B. Daca Ker f =
0, adica f este injectiv, din propozitia 2.4 rezulta
ca A este izomorf cu
f = B. Daca Ker f =
0, adica f este injectiv, din propozitia 2.4 rezulta
ca A este izomorf cu 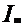 f si deci A
poate fi identificat cu imaginea sa in B, adica putem considera pe A ca un
subinel al lui B, ceea ce se face de obicei. Reciproc, daca A este un
subinel al lui B, atunci injectia canonica A→B
este evident un morfism injectiv de inele.
f si deci A
poate fi identificat cu imaginea sa in B, adica putem considera pe A ca un
subinel al lui B, ceea ce se face de obicei. Reciproc, daca A este un
subinel al lui B, atunci injectia canonica A→B
este evident un morfism injectiv de inele.
Vom introduce o alta
notiune importanta in teoria inelelor, care se obtine prin
"dualizarea" observatiei precedente, adica vom numi inel factor (sau cat) al inelului A un inel A' impreuna cu morfism
surjectiv de inele p:
A→ A'. Morfismul surjectiv p se numeste morfismul canonic sau surjectia canonica. Sa observam ca daca A
este inel comutativ orice inel factor A' al sau este inca comutativ.
In adevar,fie  β A'; atunci, din faptul ca p este morfism surjectiv,
rezulta ca exista a,b A astfel ca p(a) =
β A'; atunci, din faptul ca p este morfism surjectiv,
rezulta ca exista a,b A astfel ca p(a) = p(b) = β, unde p: A→ A' este morfismul canonic. Atunci din relatia
p(b) = β, unde p: A→ A' este morfismul canonic. Atunci din relatia  β = p(a) p(b) = p(ab) = p(ba) = p(b) p(a) = β
β = p(a) p(b) = p(ab) = p(ba) = p(b) p(a) = β verificata datorita faptului ca A este inel comutativ,
rezulta afirmatia de mai sus. In mod analog, daca A este inel unitar, atunci si A' este
inel unitar, iar morfismul canonic p este unitar. Pentru a arata acest
lucru,este suficient sa aratam ca daca 1 este
elementul unitate din A, atunci p(1) este element unitate in A'. Fie
verificata datorita faptului ca A este inel comutativ,
rezulta afirmatia de mai sus. In mod analog, daca A este inel unitar, atunci si A' este
inel unitar, iar morfismul canonic p este unitar. Pentru a arata acest
lucru,este suficient sa aratam ca daca 1 este
elementul unitate din A, atunci p(1) este element unitate in A'. Fie  A'. Atunci,daca a A este astfel ca
A'. Atunci,daca a A este astfel ca
p(a) = avem p(1) p(1) p(a) = p(1a) = p(a) =
avem p(1) p(1) p(a) = p(1a) = p(a) = 
De
asemenea, trebuie sa mentionam ca daca A' este inel factor al inelui A, atunci
retinand doar structurile de grupuri aditive ale lui A si A', se vede ca A' este grup factor al lui A. La fel, in
acest caz, A' este si o multime factor a
multimii A. Daca A' este un inel factor al lui A de morfism canonic p: A→ A', atunci vom nota acest lucru si prin (A',p) punand astfel in
evidenta si morfismul canonic.
Propozitia
2.7. (Proprietatea de universalitate a inelelor factor). Fie p: A→ A' un inel factor al inelului A si φ
A→B un morfism de inele.
i)
Exista un morfism de inele u: A'→ B astfel ca up = φ, adica astfel incat diagrama
A
 A'
A'

 u
u
B
sa fie comutativa daca si numai
daca Ker 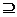 Ker p. In cazul in care u
exista, el este unic.
Ker p. In cazul in care u
exista, el este unic.
ii)Daca
exista morfismul de inele u cu proprietatea din i), atunci u este surjectiv daca
si numai daca este surjectiv, adica (B, φ) este si el inel
factor al lui A.
iii)Daca
exista morfismul de inele u cu proprietatea din i), atunci u este injectiv daca si numai
daca Ker p = Ker
Demonstratie. Folosind propozitia
II.3.5, este suficient sa aratam ca daca exista
morfismul de grupuri u, atunci le este morfism de
inele. Fie  A' si a,b A astfel ca p(a) =
A' si a,b A astfel ca p(a) = si p(b) β . Atunci:p
si p(b) β . Atunci:p
u( u(p(a)p(b)) = (up)(ab) = φ (ab) = (a) (b) = (up)(a)(up)(b) = u(
u(p(a)p(b)) = (up)(ab) = φ (ab) = (a) (b) = (up)(a)(up)(b) = u( )u(β
)u(β
Corolarul
2.8. Fie (A', p') si (A', p'), doua inele
factor ale inelului A. Atunci exista un izomorfism de inele u: A' → A', astfel ca up' = p' daca
si numai daca Ker p' = Ker p'.
Teorema
2.9. Fie A un inel si I un ideal bilateral al lui A. Atunci
exista un inel A' si un morfism surjectiv de inele A→A' astfel incat Ker = I.
Demonstratie. Consideram pe A ca grup aditiv. Atunci I este subgrup al lui A si consideram grupul factor A' A∕I, iar A→A' morfismul canonic de grupuri, care stim
(cap. II, § 3) ca are proprietatea Ker = I. Vom
arata ca pe A' putem
introduce o structura de inel astfel ca sa fie morfism de inele. In adevar, fie  β A' si fie a
β A' si fie a  si b β. Deci
si b β. Deci  a + I, β =b I, atunci
definim
a + I, β =b I, atunci
definim  β ab
+ I. Clasa produsului nu depinde de
elementele a si b alese in
clasele respective. Caci daca a' ≡ a (mod I) si b'≡ b (mod I), atunci a' = a + c, b' = b + d, cu c, d I, deci a'
b' = ab + cb + ad + cd si, deoarece I este ideal bilateral in A, cb + ad cd I, deci a'
b'≡ ab (mod I). Aceasta operatie este asociativa
pe A', deoarece operatia de
inmultire pe A este asociativa, are
element unitate daca A are element unitate si este
distributiva
fata de adunarea pe A', deoarece inmultirea pe A este, distributiva fata de adunare. Avem, de
asemenea:
β ab
+ I. Clasa produsului nu depinde de
elementele a si b alese in
clasele respective. Caci daca a' ≡ a (mod I) si b'≡ b (mod I), atunci a' = a + c, b' = b + d, cu c, d I, deci a'
b' = ab + cb + ad + cd si, deoarece I este ideal bilateral in A, cb + ad cd I, deci a'
b'≡ ab (mod I). Aceasta operatie este asociativa
pe A', deoarece operatia de
inmultire pe A este asociativa, are
element unitate daca A are element unitate si este
distributiva
fata de adunarea pe A', deoarece inmultirea pe A este, distributiva fata de adunare. Avem, de
asemenea:
(ab)= ab+ I, iar (a) (b) = (a I)(b + I) =
ab +1
pentru
orice a,b A, deci este morfism de inele. Inelul construit in teorema precedenta
se numeste inelul factor (cit) a lui A in raport cu idealul
bilateral I si se noteaza prin A∕I sau 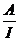 .
.
Corolarul 2.10. Daca f: A B este un
morfism de inele, atunci exista un izomorfism canonic: ׃A/Ker
f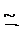 Im f
Im f
Demonstratie. Fie f': A Im f
morfismul de inele dedus din f prin restrangerea
codomeniului.Se observa imediat ca f' este surjectiv si
ca Ker f'= Ker f,adica Im f
este un inel factor al lui A in raport cu Ker
f si din corolarul2.8 rezulta afirmatia.
larul 2.8
rezulta afirmatia. Corolarul Fie A un inel si I 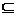 J doua
ideale bilaterale ale sale. Atunci exista un izomorfism canonic de
inele:
J doua
ideale bilaterale ale sale. Atunci exista un izomorfism canonic de
inele:
A|I

 Ψ: A|J
Ψ: A|J
J|I Demonstratia este analoaga
demonstratiei corolarului .3.10, folosind propozitia 2. 7 si
corolarul 2.10, sau se deduce direct din corolaruL.3.10 demonstrand ca in
acest caz Ψ este izomorfism de inele. Din cele de mai sus rezulta
ca subinelul, idealul bilateral si inelul factor in teoria inelelor sunt notiuni
analoage celor de subgrup, subgrup normal, grup factor in teoria grupurilor.
Propozitia 2. 12 .Fie A un inel unitar
si I un ideal stang (drept sau bilateral). Atunci I=A daca si
numai daca I contine un element inversabil din A.
Demonstratie. Daca
I=A, atunci evident I contine orice element inversabil din A. Reciproc,
sa presupunem ca I este ideal stang si contine un element
inversabil u. Deci
exista u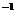
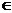 A astfel ca u u
A astfel ca u u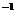 = u
= u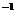 u = 1.Atunci avem u
u = 1.Atunci avem u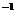 u = 1
u = 1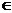 I (deoarece u
I (deoarece u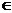 I ), deci pentru
orice element a
I ), deci pentru
orice element a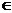 A avem a =a ∙ 1
A avem a =a ∙ 1 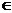 I . Fie
A un inel unitar nenul si M =
I . Fie
A un inel unitar nenul si M = 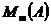 inelul
matricelor patrate de ordinul m>1. Dupa cum stim, M este un inel necomutativ. Vom de un exemplu
de ideal stang in acest inel care nu este ti ideal drept. Fie I
multimea matricelor din M ale
caror elemente de pe prima coloana sunt toate egale cu 0. Se verifica
imediat ca I este un ideal stang in M. I nu este ideal drept pentru
ca:
inelul
matricelor patrate de ordinul m>1. Dupa cum stim, M este un inel necomutativ. Vom de un exemplu
de ideal stang in acest inel care nu este ti ideal drept. Fie I
multimea matricelor din M ale
caror elemente de pe prima coloana sunt toate egale cu 0. Se verifica
imediat ca I este un ideal stang in M. I nu este ideal drept pentru
ca:

 =
= 
Evident prin schimbarea
liniilor cu coloanele se obtine un ideal drept al inelului M, care nu este
un ideal sting.
Propozitia
2.13. Fie A≠ inel
unitar, comutativ si finit si a 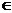 A. Atunci a este sau divizor al lui zero sau
element inversabil.
A. Atunci a este sau divizor al lui zero sau
element inversabil.
Demonstratie. Consideram functia f: A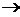 A, definita prin f(b) = ab pentru orice b
A, definita prin f(b) = ab pentru orice b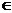 A. Daca a nu este divizor
al lui zero, atunci f este
injectiva, caci din ab = ab' rezulta b= b'. A fiind
insa multime finita, rezulta ca f este
si functie surjectiva, deci exista a'
A. Daca a nu este divizor
al lui zero, atunci f este
injectiva, caci din ab = ab' rezulta b= b'. A fiind
insa multime finita, rezulta ca f este
si functie surjectiva, deci exista a' 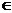 A astfel ca f(a') = 1, deci aa' = si a este inversabil
in A.
A astfel ca f(a') = 1, deci aa' = si a este inversabil
in A.
Corolarul
2.14. Un inel integru finit are toate elementele
nenule inversabile.




