Primitivele functiilor elementare
Primitiva
In analiza matematica,
o primitiva sau integrala nedefinita a
unei functii f este o functie F a carei derivata este egala cu f, adica, F ′ =f. Procesul de calcul
al primitivelor se numeste primitivare (sau integrare nedefinita). Primitivele
sunt legate de integralele
definite printeorema
fundamentala a calculului integral, si furnizeaza un mijloc
convenabil de calcul al integralelor definite ale multor functii.
Exemplu
Functia F(x)
= x3/3 este o
primitiva pentru f(x)
= x2. Intrucat
derivata unei constante este zero, x2 va avea un numar infinit de primitive; astfel (x3/3)
+ 0, (x3 / 3) +
7, (x3 / 3)
− 42, etc. Astfel, intreaga familie de primitive ale lui x2 se poate obtine prin modificarea
valorii lui C in F(x)
= (x3 / 3) + C; unde C este o constanta
arbitrara cunoscuta drept constanta de
integrare. Esential este ca graficul fiecarei primitive a unei
functii date este o translatie
pe verticala ale unei alte
functii din familie, locatia fiecarei primitive fiind data
de valoare a lui C.
Utilizari si proprietati
Primitivele sunt importante deoarece pot fi utilizate la calculul integralelor definite, folosind teorema fundamentala a calculului
integral: dacaF este
o primitiva a unei functii integrabile f, atunci:
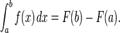
Din acest motiv, una din infinit de multele primitive ale unei
functii date f este uneori numita
'integrala generala' sau 'integrala
nedefinita' a lui f si este scrisa folosind
simbolul de integrala fara limite:
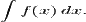
Daca F este o primitiva a lui f, si f este definita pe un interval, orice alta
primitva G a lui f difera de F printr-o constanta:
exista un numar Castfel
incat G(x) = F(x) + C oricare ar fi x. C este numita constanta
de integrare. Daca domeniul lui F este o reuniune de doua sau mai multe intervale disjuncte, atunci se pot alege
constante de integrare diferite pentru fiecare interval. De exemplu
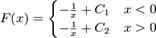
este primitiva cea mai generala pentru f(x)
= 1 / x2 pe domeniul sau general 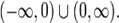
Toate functiile
continue f admite primitive, iar o primitiva F este data de integrala definita f cu limita de sus variabila:
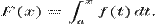
Varierea limitei de jos produce alte primitive (dar nu neaparat pe
toate). Aceasta este o alta formulare a teoremei
fundamentale a calculului integral.
Exista multe functii ale caror primitive, desi
exista, nu pot fi exprimate in termeni de functii elementare [2]. Astfel de exemple sunt
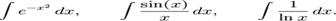
Tehnici de integrare
Calculul primitivelor functiilor elementare este adesea considerat
mai dificil decat gasirea derivatelor acestora. Pentru unele functii
elementare, este imposibil sa se exprime primitivele in termeni de alte
functii elementare.
Avem la dispozitie mai multe metode:
- liniaritatea
integrarii ne permite
sa descompunem integrale mai complexe in altele mai simple
- integrarea
prin substitutie, adesea combinata cu identitatile trigonometrice sau cu logaritmul natural
- integrarea
prin parti pentru
integrarea produsului de functii
- metoda fractiilor partiale permite integrarea tuturor functiilor rationale (fractii de doua polinoame)
- algoritmul
Risch
-
integralele pot fi cautate intr-un tabel
de integrale
- la
integrarea multipla, se pot folosi si alte tehnici aditionale,
vezi de exemplu integralele duble si coordonatele polare, Jacobianul siteorema lui Stokes
-
Sistemele algebrice pe calculator se pot folosi pentru a automatiza
partial sau total munca depusa in tehnicile simbolice de mai sus,
ceea ce e deosebit de util cand manipularile algebrice implicate sunt
foarte complexe sau laborioase
-
daca o functie nu are primitive elementare (de exemplu, exp(x2)),
integralele sale definite pot fi aproximate folosind integrarea numerica
Primitivele functiilor discontinue
Pentru a ilustra unele din subtilitatile teoremei fundamentale, se poate
observa ce fel de functii discontinue admit primitive. Chiar daca
sunt inca intrebari fara raspuns in aceasta
zona, se stie ca:
Unele
functii patologice cu multimi mari de discontinuitati ar
putea admite totusi primitive.
In unele
cazuri, primitivele unor astfel de functii pot fi gasite prin integrare Riemann, pe cand in alte
cazuri astfel de functii nu sunt integrabile Riemann.
Sa presupunem ca functiile despre care vorbim sunt definite
pe intervale deschise.
O
conditie necesara, dar nu suficienta, pentru ca o functie f sa admita primitiva
este ca f sa aiba proprietatea Darboux. Adica,
daca [a,b] este un subinterval al domeniului de
definitie al lui f si d este un numar real intre f(a) si f(b), atunci exista
un c intre a si b astfel incat f(c)=d. Pentru a
vedea aceasta, fie F o primitiva a lui f si sa consideram
functia continua g(x)=F(x)-dx pe intervalul inchis [a, b]. Atunci g trebuie sa aiba fie un
minim, fie un maxim c in intervalul deschis (a,b)
si astfel 0=g′(c)=f(c)-d.
Multimea
discontinuitatilor lui f trebuie sa fie o multime neglijabila.
Aceasta multime trebuie sa fie si multime F-sigma (pentru ca multimea
discontinuitatilor unei functii trebuie sa fie de acest
fel). Mai mult, pentru orice multime F-sigma neglijabila, se poate
construi o functie f care are o primitiva, si
care are multimea data ca multime de discontinuitati.
Daca f admite primitive, este marginita pe subintervale inchise finite ale
domeniului de definitie si are o multime de
discontinuitati demasura Lebesgue 0, atunci se poate gasi o
primitiva prin integrare.
Daca f admite o primitiva F pe un interval inchis [a,b],
atunci oricum s-ar alege o partitie 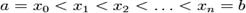 , daca se aleg puncte
, daca se aleg puncte 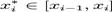 asa
cum este specificat in Teorema de
medie, atunci suma Riemann corespunzatoare tinde la valoarea F(b)-F(a).
asa
cum este specificat in Teorema de
medie, atunci suma Riemann corespunzatoare tinde la valoarea F(b)-F(a).
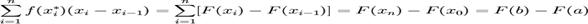
Totusi daca
multimea discontinuitatilor lui f are masura Lebesgue
pozitiva, la o alta alegere a punctelor intermediare 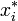 se obtine o valoare semnificativ
diferita de suma Riemann, indiferent cat de fina este partitia.
Vezi exemplul 4 de mai jos.
se obtine o valoare semnificativ
diferita de suma Riemann, indiferent cat de fina este partitia.
Vezi exemplul 4 de mai jos.
Exemple
- Functia
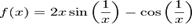
cu 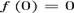 nu este continua in x dar admite primitiva
nu este continua in x dar admite primitiva
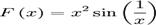
cu 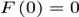 .
Deoarece f este marginita pe intervale
finit inchise si este discontinua doar in 0, primitiva F se poate obtine prin integrare:
.
Deoarece f este marginita pe intervale
finit inchise si este discontinua doar in 0, primitiva F se poate obtine prin integrare: 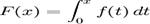 .
.
- Functia
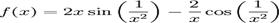
cu 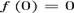 nu este continua in x dar admite primitiva
nu este continua in x dar admite primitiva
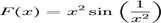
cu 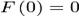 .
Spre deosebire de exemplul 1, f(x)
este nemarginita in orice interval ce il contine pe 0, deci
integrala Riemann nu este definita pe aceste intervale.
.
Spre deosebire de exemplul 1, f(x)
este nemarginita in orice interval ce il contine pe 0, deci
integrala Riemann nu este definita pe aceste intervale.
Daca f(x)
este functia din exemplul 1 si F este o primitiva a ei, si 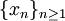 este o multime densa numarabila a intervalului deschis
este o multime densa numarabila a intervalului deschis 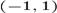 ,
atunci functia
,
atunci functia
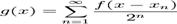
admite o primitiva
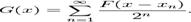
Multimea de discontinuitati a lui g este exact multimea 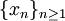 .
Deoarece g este marginita pe intervale
finite inchise si multimea de discontinuitati are
masura 0, primitiva G poate fi gasita prin
integrare.
.
Deoarece g este marginita pe intervale
finite inchise si multimea de discontinuitati are
masura 0, primitiva G poate fi gasita prin
integrare.
- Fie
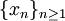 o
submultime densa numarabila a
intervalului deschis
o
submultime densa numarabila a
intervalului deschis 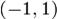 . Consideram functia strict
crescatoare si continua
. Consideram functia strict
crescatoare si continua
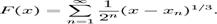
Se poate arata ca
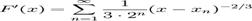
pentru toate valorile x unde seria este convergenta,
si si ca graficul F(x)
are tangenta verticala in toate celalte valori ale lui x. In particular graficul are
tangente verticale in toate punctele din multimea 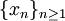 .
.
Mai mult 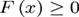 pentru
toti x unde derivata este definita.
Rezulta ca functia inversa G F este derivabila in toate punctele
si ca
pentru
toti x unde derivata este definita.
Rezulta ca functia inversa G F este derivabila in toate punctele
si ca
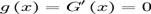
oricare ar fi x in multimea 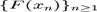 care este densa in intervalul
care este densa in intervalul 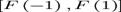 .
Astfel gadmite o
primitiva G. Pe de
alta parte, nu se poate ca
.
Astfel gadmite o
primitiva G. Pe de
alta parte, nu se poate ca
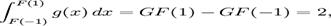
fiindca pentru orice partitie 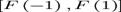 ,
se pot alege puncte intermediare pentru suma Riemann din multimea
,
se pot alege puncte intermediare pentru suma Riemann din multimea 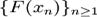 ,
care dau valoarea 0 sumei. Rezulta ca g are multimea de
discontinuitati cu masura Lebesgue pozitiva. Figura 1
din dreapta arata o aproximare a graficului g(x) unde
,
care dau valoarea 0 sumei. Rezulta ca g are multimea de
discontinuitati cu masura Lebesgue pozitiva. Figura 1
din dreapta arata o aproximare a graficului g(x) unde 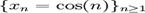 iar
seria este trunchiata la 8 termeni. Figura 2 arata graficul unei
aproximari a primitivei G(x),
si ea trunchiata la 8 termeni. Pe de alta parte daca
integrala Riemann este inlocuita deintegrala Lebesgue, atunci lema lui Fatou sau teorema
convergentei dominate arata
ca g satisface teoreme fundamentala in
acest context.
iar
seria este trunchiata la 8 termeni. Figura 2 arata graficul unei
aproximari a primitivei G(x),
si ea trunchiata la 8 termeni. Pe de alta parte daca
integrala Riemann este inlocuita deintegrala Lebesgue, atunci lema lui Fatou sau teorema
convergentei dominate arata
ca g satisface teoreme fundamentala in
acest context.
In exemplele 3 si 4, multimile de
discontinuitati ale functiilor g sunt dense doar intr-un interval
deschis finit 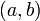 .
Totusi aceste exemple pot fi usor modificate pentru a avea
multimi de discontinuitati dense pe intreaga dreapta
reala
.
Totusi aceste exemple pot fi usor modificate pentru a avea
multimi de discontinuitati dense pe intreaga dreapta
reala 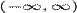 .
Let
.
Let
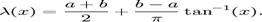
Atunci 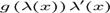 are o multime densa de
discontinuitati pe
are o multime densa de
discontinuitati pe 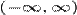 si are primitiva
si are primitiva 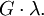
Printr-o
metoda similara cu cea din exemplul 5, se poate modifica g in exemplul 4 ca sa dispara
pentru toate numerele
rationale. Daca se foloseste o versiune simplificata a integralei Riemann definita ca limita sumelor
Riemann sums la stanga sau ka dreapta pe partitii regulate, se va
obtine ca integrala unei astfel de functii g peste un interval 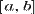 este 0 oricand a si b sunt ambele rationale, in loc de
este 0 oricand a si b sunt ambele rationale, in loc de  .
Astfel teorema fundamentala esueaza spectaculos.
.
Astfel teorema fundamentala esueaza spectaculos.
Note
Primitivele
se mai numesc si integrale generale, si uneori
simplu integrale. Cel din urma termen este generic, si nu se
refera doar la integralele nedefinite (primitive), ci si la integralele definite. Cand este
utilizat cuvantul integrala,
fara alte specificatii, cititorul trebuie sa deduca
din context daca referirea este la o integrala definita sau
nedefinita. Unii autori definesc integrala nedefinita a unei
functii ca fiind multimea tuturor primitivelor posibile ale acesteia.
Altii o definesc ca fiind un element ales arbitrar din acea multime.
Wikipedia adopta aceasta din urma abordare. Functiile elementare includ polinomialele, exponentialele, logaritmii, trigonometricele, functiile trigonometrice inverse si combinarile acestora

