Ideale prime si idea
maxime
Am vazut in paragrafele
precedente ca in studiul aritmeticii unui inel intervin si elemente
din teoria idealelor. Aici vom defini doua tipuri de ideale care dunt
foarte importante in intreaga matematica: ideal prim si ideal maxim.
Definitia
1. Fie A un inel comutativ unitar. Un ideal P al lui A se
numeste ideal prim daca P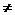 A din faptul ca
produsul a doua elemente a, b
A din faptul ca
produsul a doua elemente a, b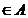 este in P rezulta ca cel putin unul
dintre aceste elemente este in P.
este in P rezulta ca cel putin unul
dintre aceste elemente este in P.
Idealul (0) este prim in inelul A
daca si numai daca A este inel integru.
In adevar, daca (0) este
ideal prim si daca a, b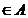 , ab=0, atunci ab
, ab=0, atunci ab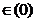 ,deci sau a
,deci sau a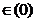 ,adica a=0, sau b
,adica a=0, sau b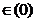 ,adica b=0. Invers, daca A este inel integru,
rezulta imediat din definitie ca (0) este ideal prim.
,adica b=0. Invers, daca A este inel integru,
rezulta imediat din definitie ca (0) este ideal prim.
Propozitia 2. Fie A un inel
integru si p un element nenul
si neinversabil din A. Atunci idealul principal pA este prim daca
si numai daca p este un element prim in A.
Demonstratie.
Presupunem ca idelul pA este prim si fie a,
b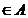 astfel incat p ab. Atunci rezulta
ca ab
astfel incat p ab. Atunci rezulta
ca ab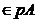 si deoarece pA este ideal prim, avem sau a
si deoarece pA este ideal prim, avem sau a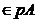 din care arata ca p a,
sau b
din care arata ca p a,
sau b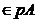 , ceea ce arata ca p b.
In plus, p nu este inversabil caci in cazul contrar ar rezulta pA=A.
, ceea ce arata ca p b.
In plus, p nu este inversabil caci in cazul contrar ar rezulta pA=A.
Reciproc, daca p este element
prim, atunci rezuta ca pA 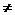 A,
altfel rezulta 1=ap, cu a
A,
altfel rezulta 1=ap, cu a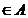 ,adica p ar fi inversabil. Fie a, b
,adica p ar fi inversabil. Fie a, b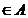 ,astfel incat a,b
,astfel incat a,b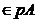 . Aceasta inseamna ca p ab,
deci p a, adica a
. Aceasta inseamna ca p ab,
deci p a, adica a 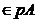 , sau p b,adica b
, sau p b,adica b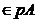 .
.
Propozitia precedenta ne
permite sa dam numeroase exemple de ideale in diverse inele. Astfel
inelul intregilor rationali Z sunt indeale prime (0) si toate
idealele generate de numerele prime si numai acestea, deoarece Z este inel
principal. Prin urmare , Z are o infinitate de ideale prime, caci
numarul numerelor prime pozitive este infinit.
In inelul intregilor lui Gauss 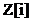 ,
idealul 2
,
idealul 2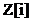 nu este prim , deoarece, dupa cum am vazut 2
este reductibil, deci nu este prim. In schimb, idealele (1-i)
nu este prim , deoarece, dupa cum am vazut 2
este reductibil, deci nu este prim. In schimb, idealele (1-i) 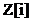 ,(1+i)
,(1+i) 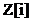 li 3
li 3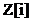 sunt prime, deoarece am aratat ca elementele
1-I, 1+I li 3 sunt ireductibile in
sunt prime, deoarece am aratat ca elementele
1-I, 1+I li 3 sunt ireductibile in 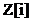 si cum
si cum 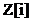 este inel
factorial, rezulta ca elementele ireductibile sunt si prime. De
asemenea si idealul (0) este prim caci
este inel
factorial, rezulta ca elementele ireductibile sunt si prime. De
asemenea si idealul (0) este prim caci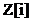 este
integru. Daca k este un corp, atunci inelul k[X]
orice ideal generat de un olinom de gradul 1 este prim. De asemenea, este
evident prim si idealul nul.
este
integru. Daca k este un corp, atunci inelul k[X]
orice ideal generat de un olinom de gradul 1 este prim. De asemenea, este
evident prim si idealul nul.
Daca A este un inetgru si
p un element prim in A atunci idelul p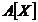 din
din 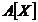 este prim. In
adevar, din 4.8 rezulta ca p este prim si in inelul
este prim. In
adevar, din 4.8 rezulta ca p este prim si in inelul 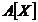 si
afirmatia rezulta din propozitia precedenta.
si
afirmatia rezulta din propozitia precedenta.
Propozitia 3. Fie 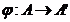 un morfism de
inele.
un morfism de
inele.
i)
Daca P' este ideal
prim in A',P=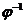 (P')
este idel prim in A.
(P')
este idel prim in A.
ii)
Daca,
in plus,  este surjectiv
si P este ideal prim in A astfel incat P
este surjectiv
si P este ideal prim in A astfel incat P 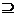 Ker
Ker  , atunci P'=
, atunci P'= (P) este ideal prim in A'.
(P) este ideal prim in A'.
Demonstratie. i) Stim ca P=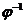 (P')
este ideal in A. Sa demonstram acum ca P este ideal prim. Fie a, b
(P')
este ideal in A. Sa demonstram acum ca P este ideal prim. Fie a, b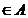 astfel incat ab
astfel incat ab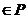 . Atunci
. Atunci  (ab)=
(ab)=
 (a)
(a) (b)
(b) 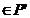 si deci sau
si deci sau  (a)
(a) 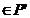 , adica a
, adica a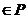 , sau
, sau  (b)
(b) 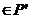 , adica b
, adica b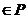 , deoarece P' este ideal prim in A'. Avem de asemenea P
, deoarece P' este ideal prim in A'. Avem de asemenea P 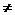 A,
caci
A,
caci  (1)1
(1)1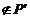
iii)
Stim ca P'= (P)
este ideal in A'. Sa aratam ca P' este ideal prim. Fie a', b'
(P)
este ideal in A'. Sa aratam ca P' este ideal prim. Fie a', b'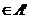 astfel incat a', b'
astfel incat a', b'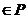 si fie a, b
si fie a, b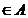 astfel incat
astfel incat (ab)=
(ab)=
 (a)
(a) (b)= a' b'
(b)= a' b'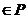 , adica ab=p+c, unde p
, adica ab=p+c, unde p 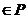 si c
si c 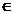 Ker
Ker
 . Deoarece P
. Deoarece P 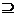 Ker
Ker  , avem ca ab
, avem ca ab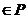 si deoarece P este
ideal prim, rezulta ca a
si deoarece P este
ideal prim, rezulta ca a 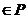 sau b
sau b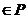 . Atunci rezulta ca
. Atunci rezulta ca  (a)=a'
(a)=a'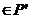 sau
sau  (b)=
b'
(b)=
b'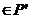 . P
. P 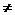 A,
caci daca 1
A,
caci daca 1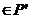 , atunci rezulta
ca exista a
, atunci rezulta
ca exista a 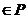 astfel incat
astfel incat  (a)=1,
deci
(a)=1,
deci  (a-1)=0, adica a-1
(a-1)=0, adica a-1 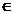 Ker
Ker 
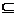 P, deci 1
P, deci 1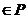
Corolarul 4. Fie a un inel si I un ideal al sau. Atunci
urmatoarele doua afirmatii sunt echivalente:
a)
I este ideal prim.
b)
Inelul factor A I
este integru.
Rezulta din
propozitia precedenta, tinand cont de faptul ca daca
notam cu 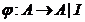 surjectia canonica, atunci Ker
surjectia canonica, atunci Ker  =I si (Ker
=I si (Ker  )=(0).
)=(0).
Definitia Fie A un inel si M un ideal al sau.
Se spune ca M este ideal maxim in A daca M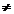 A oricare ar fi idealul I
al lui A, cu A
A oricare ar fi idealul I
al lui A, cu A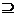 I
I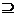 M, rezulta I=A sau I=M. Cu alte cuvinte idealele
maximale sunt elementele maximale din multimea ordonata cu incluziunea
a idealelor din A diferite de A .
M, rezulta I=A sau I=M. Cu alte cuvinte idealele
maximale sunt elementele maximale din multimea ordonata cu incluziunea
a idealelor din A diferite de A .
Deoarece
corpurile comutative sunt caracterizate prin faptul ca au doua ideale
distincte, rezulta ca idealul (0) dintr-un inel A (comutativ) este maximal daca si numai
daca A este corp.
Propozitia 6. Fie A un inel
principal care nu este corp si p un element nenul si neinversabil din A. Atunci idealul pA
este maximal daca si numai daca p este ireductibil.
Demonstratie.
Reamintim ca A fiind principal, orice element ireductibil este prim.
Daca p este ireductibil, atunci rezulta ca pA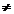 A. Fie I un inel al lui A
astfel incat A
A. Fie I un inel al lui A
astfel incat A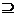 I
I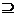 pA.
Deoarece a este inel principal, exista un element a
pA.
Deoarece a este inel principal, exista un element a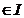 astfel incat I=aA. Din faptul ca aA
astfel incat I=aA. Din faptul ca aA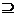 pA
rezulta ca exista a'
pA
rezulta ca exista a'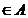 astfel incat p=aa' si
deoarece p este ireductibil, avem ca p este sau asociat , cu a, sau a este element inversabil in A. In primul
caz rezulta aA=pA, iar in al doilea caz aA=A si prima afirmatie
a propozitiei este demonstrata. Fie acum M un ideal maximal in A. Deoarece A este inel principal,
rezuta ca exista a
astfel incat p=aa' si
deoarece p este ireductibil, avem ca p este sau asociat , cu a, sau a este element inversabil in A. In primul
caz rezulta aA=pA, iar in al doilea caz aA=A si prima afirmatie
a propozitiei este demonstrata. Fie acum M un ideal maximal in A. Deoarece A este inel principal,
rezuta ca exista a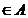 astfel incat M=aA. Vom arata ca a este
element ireductibil. Deoarece A este inel factorial, rezulta ca
exista un element ireductibil p al inelului A astfel incat p sa
divida pe a. Atunci A
astfel incat M=aA. Vom arata ca a este
element ireductibil. Deoarece A este inel factorial, rezulta ca
exista un element ireductibil p al inelului A astfel incat p sa
divida pe a. Atunci A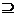 pA
pA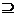 aA si deoarece pA
aA si deoarece pA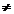 A, rezulta ca
pA=aA, deci a este ireductibil.
A, rezulta ca
pA=aA, deci a este ireductibil.
Propozitia
precedenta ne furnizeaza
numeroase exemple de ideale maximale in diverse inele principale. Astfel, in
inelul intregilor Z sunt ideale maximale idealele generate de numere prime
si numai acestea, iar (0) nu este ideal maximal caci Z nu este corp. In
inelul intregilor lui Gauss 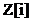 ,
idealele principale generate de
3,1-i,1+i sunt ideale maximale deoarece aceste
elemente sunt ireductibile iar
,
idealele principale generate de
3,1-i,1+i sunt ideale maximale deoarece aceste
elemente sunt ireductibile iar 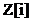 este inel
principal. Pe de alta parte, idealul generat de 2 in
este inel
principal. Pe de alta parte, idealul generat de 2 in 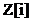 nu este maximal,
deoarece 2 nu este ireductibil.
nu este maximal,
deoarece 2 nu este ireductibil.
Daca
k este un corp, atunci in inelul 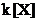 , care este principal, idealele maximale coincid cu
idealele generate de polinoamele ireductibile. In particular, idelalele
generate de polinoamele de gradul 1 sunt maximale.
, care este principal, idealele maximale coincid cu
idealele generate de polinoamele ireductibile. In particular, idelalele
generate de polinoamele de gradul 1 sunt maximale.
Propozitia 7. Fie 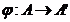 un morfism
surjectiv de inele.
un morfism
surjectiv de inele.
i)
Daca M' este ideal
maximal in A', atunci M=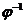 (M')
este ideal maximal in A.
(M')
este ideal maximal in A.
ii)
Daca
M este ideal maximal in A astfel incat Ker 
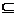 M, atunci M'=
M, atunci M'=  (M) este ideal maximal in A'.
(M) este ideal maximal in A'.
Demonstratie.
Afirmatiile rezulta din faptul ca multimile ordonate ale
idealelor lui A' si idealelor lui A care contin pe Ker  sunt izomorfe,
deci elementele maximale din cele doua multimi ordonate se corespund.
sunt izomorfe,
deci elementele maximale din cele doua multimi ordonate se corespund.
Corolarul 8. Fie A un inel si M un ideal in A. Atunci
urmatoarele afirmatii sunt echivalente:
a)
M
este ideal maximal in A;
b)
Inelul
factorial A|M este corp.
Aplicand
teorema precedenta pentru morfismul canonic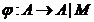 , rezulta ca M este maximal in A daca
si numai daca (0) este ideal maximal in A|M si acest fapt este
echivalent cu acela ca A|M este corp.
, rezulta ca M este maximal in A daca
si numai daca (0) este ideal maximal in A|M si acest fapt este
echivalent cu acela ca A|M este corp.
Corolarul
9. Orice ideal maximal al unui inel este si ideal prim.
In
adevar, din corolarul precedent rezulta ca M este ideal maximal
in A, atunci A|M este corp, deci este in particular inel integru si
afirmatia corolarului rezulta din 4.
Nu
orice ideal prim este maximal, caci, de exemplu, in inelul Z, (0) este
ideal prim dar nu este maximal.
Propozitia 10. Daca A este un
inel si I este idealul sau, I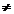 A, atunci exista un
ideal maximal M in A astfel icat M
A, atunci exista un
ideal maximal M in A astfel icat M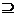 I.
I.
Demonstratie. Daca
consideram muItimea idealelor din A, distincte de A, care contin
pe I cu relatia de incluziune, obtinem o multime ordonata
care este inductiva (v. Cap.I,2). In adevar daca 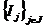 este o
multime total ordonata de
ideale din A cu
este o
multime total ordonata de
ideale din A cu 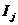
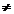 A si
A si 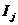
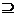 I, atunci I'=
I, atunci I'=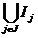 este ideal in A (de verifica ca in
demonstratia lemei 3.8) si 1
este ideal in A (de verifica ca in
demonstratia lemei 3.8) si 1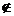
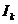 . Prin urmare, I'
. Prin urmare, I'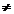 A. Aplicand lema lui Zorn
(cap.I,2), rezulta ca aceasta multime are un element
maximal, care va fi evident ideal maximal in A si contine pe I.
A. Aplicand lema lui Zorn
(cap.I,2), rezulta ca aceasta multime are un element
maximal, care va fi evident ideal maximal in A si contine pe I.
Din propozitia 2 si
teorema 3.7 rezulta ca intr-un inel principal orice ideal este
produsul unui numar finit de ideale prime si din lema 4.2
rezulta ca aceasta descompunere este unica exceptand
ordinea factorilor.

