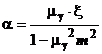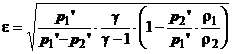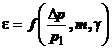PRELUCRAREA DATELOR EXPERIMENTALE.
DETERMINAREA RELATIILOR MATEMATICE PENTRU EXPRIMAREA
REZULTATELOR EXPERIMENTALE.
Estimarea valorii adevarate a unei marimi
masurate direct intr-un proces experimental si calculul indicilor de
precizie
Intr-un
proces de cercetare experimentala care are ca scop determinari cantitative ale
uneia sau mai multor marimi, se efectueaza un numar finit de masurari cu o
suficienta precizie, mentinand aceleasi conditii (metodologie
si mijloace experimentale, mediu ambiant etc).
Una
din principalele probleme ale prelucrarii datelor experimentale - respectiv
prima din acestea, in ordinea efectuarii lor - este estimarea adevaratelor
valori ale marimilor masurate pe baza rezultatelor obtinute.
Deci,
in general, dupa masurarea repetata - in aceleasi conditii a unei
marimi X si obtinerea unui sir de valori X1, X2,
. Xn, fiecare din ele continand o anumita eroare necunoscuta,
se pune problema estimarii valorii adevarate a acestei marimi, cu o eroare cat
mai mica posibila. De mentionat, ca numai intamplator rezultatul uneia din
aceste masurari ar putea coincide cu valoarea adevarata a marimii masurate.
Conform
standardelor in vigoare, valoarea adevarata a unei marimi este valoarea exacta
a acesteia, fara erori. Stabilirea ei este insa inaccesibila experimentarilor
datorita unor incertitudini cauzate de o serie de factori precum: imperfectiuni
ale teoriei pe care se bazeaza experimentarile si ale mijloacelor de
cercetare, imperfectiuni ale operatorului (experimentatorului) etc.
Pentru
a putea folosi o valoare masurata oarecare Xi din sirul
mentionat mai inainte este necesar sa se aprecieze valoarea probabila a
erorii xi, exprimata de relatia:
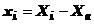
in
care: Xa reprezinta valoarea adevarata a marimii masurate.
Pentru
estimarea erorilor asociate probabil unei valori masurate oarecare exista, ca
principiu, doua metode, cunoscute sub denumirile:
- evaluare externa a erorilor;
- evaluare interna a erorilor.
Evaluarea externa este foarte dificila si incerta deoarece necesita estimarea
erorilor corespunzatoare tuturor surselor de erori care pot interveni, iar apoi
pentru obtinerea valorii rezultante trebuie ca erorile partiale sa
fie compuse tinand seama daca sunt dependente sau independente intre ele
si de faptul ca unele din acestea pot fi de un sens, altele de alt sens
sau sa aiba o directie oarecare.
Evaluarea interna a erorilor se bazeaza pe analiza statistica a rezultatelor obtinute
in cursul experimentarilor. Aceasta metoda este mai putin dificila si
mai certa, dar necesita sa fie cunoscuta legea de distributie a
frecventelor rezultatelor masurarilor.
Astfel,
daca se considera ca la masurarea unei marimi oarecare X se fac 16 masuratori
in aceleasi conditii si ca distributia frecventelor
valorilor rezultate este cea din tabelul 61, aceasta se poate reprezenta grafic
ca in figura 61.
Distributia
frecventelor valorilor rezultate la masurarea unei marimi oarecare X
Tabelul 61
|
Valorile Xi ale marimii masurate
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
Frecventele de aparitie mi ale valorilor Xi
in intervalul considerat
|
|
|
|
|
|
|
|
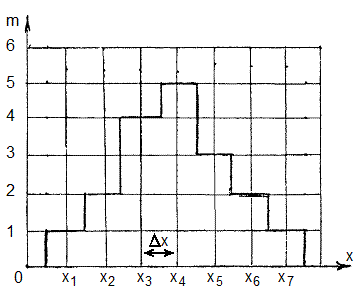
Fig.
61 - Grafic de distributie a frecventelor marimilor masurate.
Din
grafic rezulta o vedere de ansamblu asupra imprastierii valorilor si
asupra frecventei de repetare a diferitelor valori, suma celor care se afla
in intervalul minim al variatiilor marimilor, notat cu Dx, deci o vedere asupra naturii generale a
distributiei.
Intervalul
minim de variatie a marimilor depinde, in principal, de aparatura de
masurare si se alege, egal cu o diviziune a scalei de citire a acestuia.
Daca
numarul masurarilor ar fi marit la infinit, iar intervalul minim ar fi facut
cat mai mic posibil, graficul distributiei ar deveni o curba continua. Un
ansamblu limitat de masurari, respectiv 18 pentru exemplul luat, poate fi
considerat ca o proba luata din numarul infinit de mare de masurari posibile.
Ecuatia curbei distributiei rezultatelor unui numar infinit de mare
de masurari se numeste legea distributiei masurarilor.
Considerandu-se
aceasta lege si considerand ca distributia valorilor masurarilor este
afectata numai de erorile aleatoare se poate stabili valoarea cea mai probabil
adevarata a marimii masurate.
Erorile
aleatoare sunt cele care apar din cauza unei multimi de factori a caror
influenta individuala este neglijabila, din care cauza nu exista
posibilitatea depistarii si inlaturarii acestor influente. Erorile
aleatoare sunt inevitabile si nu pot fi inlaturate din rezultatele
individuale ale masurarilor. Dar cu ajutorul teoriei probabilitatilor se
poate lua in considerare in ce masura ele influenteaza estimatiile
adevaratelor valori ale marimilor, ceea ce permite determinarea valorii marimii
masurate, cu o eroare mai mica in raport cu erorile masurarilor individuale.
De
aceea, rezultatele masurarilor supuse prelucrarii matematice nu trebuie sa
contina erori grosolane si erori sistematice.
Erorile
grosolane apar datorita incalcarii principiilor generale de masurare sau
neatentiei experimentatorului. Ceea ce caracterizeaza un rezultat ce
contine o eroare grosolana este faptul ca aceasta difera esential de
rezultatele celorlalte masurari ca valoare. Odata descoperita existenta
unei erori grosolane, rezultatul masurarii respective trebuie sa fie inlaturat
si repetata masurarea. Daca nu este posibil ca rezultatele care contin
erori grosolane sa fie inlaturate in timpul desfasurarii procesului
experimental, atunci excluderea trebuie sa se faca pe baza unor criterii care
au in vedere anumite limite pe care valorile unor masurari le poate avea
fata de rezultatele celorlalte masurari.
Erorile
sistematice se datoresc unor defecte ale aparatului (de exemplu deplasarea
originii de citire sau de calcul) sau sunt provenite datorita modificarii conditiilor
exterioare (de exemplu temperatura), schimbarii metodelor de lucru etc. Deoarece
erorile sistematice au o actiune unilaterala si deosebit de
periculoasa prin efectul lor cumulatoriu, sarcina experimentatorului este de a
elimina sau cel putin de a atenua simtitor influenta acestor
erori asupra rezultatelor obtinute la masurari, introducand asupra acestor
rezultate corectiile corespunzatoare.
De
exemplu, daca dupa efectuarea masurarilor s-a depistat o reglare incorecta a
aparatului de masurat, care a condus la o deplasare a originii de calcul,
atunci toate valorile obtinute la aceste masurari vor fi corectate cu o
marime constanta in sensul invers deplasarii originii de calcul, daca scara
aparatului este uniforma, sau cu o marime care variaza dupa o anumita lege,
daca aceasta scara este neuniforma.
Dupa
ce s-a stabilit ca rezultatele masurarilor repetate ale unei marimi efectuate
intr-un proces de cercetare experimentala sunt afectate numai de erori
aleatoare, se pune problema determinarii cele mai probabile valori adevarate
acesteia. La intrebarea care este aceasta valoare se pot da diferite
raspunsuri: media aritmetica, media geometrica, media patratica, mediana, moda
sau chiar orice alta valoare din sirul de date rezultate experimental.
MEDIA ARITMETICA. Daca intr-un sir de n marimi, rezultatul X1 apare de n1
ori, X2 de n2 ori, . Xk de nk ori
deci,
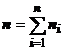
atunci
media aritmetica este data de expresia:
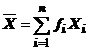 (2)
(2)
unde
fi este frecventa relativa care se calculeaza cu relatia:
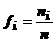 (3)
(3)
In
cazul cand in cele n masurari fiecare rezultat apare o singura data
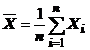 (4)
(4)
Media
aritmetica exprimata de relatia (2) se numeste media aritmetica
pentru date grupate, iar cea data de relatia (4) - medie aritmetica pentru
date negrupate.
In
majoritatea cercetarilor experimentale numarul de masurari efectuate asupra
unei marimi este relativ mic si rezultatele apar negrupate. In continuare,
pentru celelalte valori prin care poate fi estimata adevarata valoare a marimii
masurate se va lua in considerare numai cazul aparitiei negrupate a
datelor.
MEDIA GEOMETRICA este exprimata de relatia:
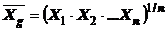 (5)
(5)
MEDIA PATRATICA se calculeaza cu relatia:
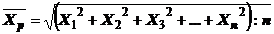 (6)
(6)
MEDIANA
este acea valoare Me pentru care se respecta probabilitatile:
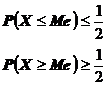 (7)
(7)
unde
X este marimea studiata.
Mediana
este deci, acea valoare a marimii respective care imparte intregul sir de
rezultate, dispuse in ordinea descrescatoare, in doua parti egale. Daca
sirul de masurari are n = 2n' + 1 rezultate, atunci mediana este elementul
de rang n' + 1, iar daca sirul contine n = 2n' rezultate, neexistand
o valoare care sa fie centrala mediana este data de media aritmetica a
rezultatelor de rang n' si n' + 1.
MODA este
acea valoare Mo din sirul de rezultate ale masurarilor unor marimi, careia
ii corespunde frecventa maxima. Uneori repartitia de frecvente
poate avea doua sau mai multe maxime, acestea denumindu-se repartitii
bimodule sau plurimodule.
Legatura
dintre media aritmetica, mediana si moda se exprima aproximativ cu
relatia:
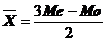 (9)
(9)
de
unde se deduc relatiile:
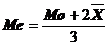 (10)
(10)
si
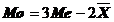 (11)
(11)
Pentru
stabilirea celei mai probabile valori a marimii masurate, care se apreciaza a
fi deci valoarea adevarata, trebuie - asa cum s-a aratat - sa fie
cunoscuta repartitia rezultatelor masurarii, respectiv repartitia
frecventelor erorilor aleatoare.
In
functie de ipotezele facute, s-au obtinut diferite forme ale legii
distributiei frecventelor, cunoscute sub denumirile: distributia
normala, distributia binomiala, distributia Poisson si altele.
Dintre
acestea, lega distributiei normale, este cel mai mult acceptata in
prelucrarea datelor cercetarilor experimentale, deoarece:
- reda distributiile marimilor masurate
intr-un numar foarte mare de cazuri;
- este relativ simpla, continand o singura
constanta arbitrara;
- alte legi de distributie se reduc la legea
normala, in anumite conditii limita.
Legea
distributiei normale a fost stabilita de Hagen pe baza unor ipoteze care corespund
foarte bine conditiilor cercetarilor experimentale si anume:
- fiecare sir de masurari ale unei
marimi este afectat, in mod inevitabil, de erori;
- fiecare din aceste erori pot fi
considerate ca fiind formate dintr-un numar de erori elementare, egale
si foarte mici;
- in fiecare masurare, orice eroare
elementara este tot atat de probabil sa intre cu semnul plus, ca si
cu semnul minus, deci probabilitatea de aparitie a erorilor pozitive
este egala cu probabilitatea de aparitie a erorilor negative.
In
cazul ipotezelor mentionate, pentru a stabili legea distributiei
normale se porneste de la un grafic asemanator cu cel din figura 61, in
care in abscisa sunt inscrise erorile x, iar in ordonata - densitatea de
repartitie y, denumita si coeficient de probabilitate al unei erori x,
care reprezinta de fapt inaltimea unui dreptunghi din grafic, la
conditia limita, cand latimea dreptunghiului tinde catre 0 si
cand deci, inaltimea este ordonata unui punct al unei curbe continue.
Densitatea
de repartitie y este definita de relatia:
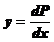 (12)
(12)
in
care dP reprezinta probabilitatea ca o eroare sa se gaseasca intre 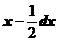 si
si 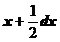 .
.
Deci,
pornind de la un astfel de grafic, se determina 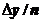 care este panta
dreptei ce uneste doua colturi adiacente ale liniei frante, se
gaseste apoi valoarea
care este panta
dreptei ce uneste doua colturi adiacente ale liniei frante, se
gaseste apoi valoarea 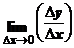 , rezultand:
, rezultand:
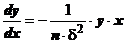 (13)
(13)
in
care:
d este jumatatea
intervalului dintre 2 marimi adiacente;
n - numarul de masurari din sirul
reprezentat de distributia respectiva.
Se
noteaza:
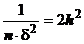 (14)
(14)
in
care h este numit modul de precizie.
Se
introduce (14) in (13) si se integreaza in raport cu x, dupa calcule
rezultand:
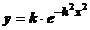 (15)
(15)
una
din formele sub care este cunoscuta legea distributiei normale.
Pentru
determinarea constantei k, procedeul se bazeaza pe consideratii de
geometrie analitica, aplicata la solidul generat de curba exprimata de
relatia (15) care se roteste in jurl ordonatei, obtinandu-se:
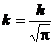 (16)
(16)
Prin
inlocuirea relatiei (16) in (15) rezulta:
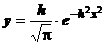 (17)
(17)
In
exprimarea legii distributiei normale se foloseste si dispersia
rezultatelor masurarilor date de abaterea medie patratica, care este legata de
modulul de precizie prin relatia:
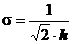 (18)
(18)
Inlocuind
in relatia (17) pe h si h2 cu expresiile rezultate din (18) se
obtine o alta exprimare a distributiei normale, adica:
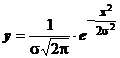 (19)
(19)
La
acelasi rezultat a ajuns Gauss, pornind de la ipoteza ca cea mai buna
aproximare a valorii adevarate a unei marimi, care a fost masurata in repetate
randuri cu aceiasi precizie, este media aritmetica a masurarilor
respective.
De
aceea, in toate cazurile in care se apreciaza ca distributia frecventelor
masurarilor (erorilor, abaterilor) se face dupa legea normala exprimata prin
relatia (17) sau (19) se considera ca cea mai probabila valoare adevarata,
media aritmetica 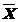 a sirului de
valori X1, X2, . Xn care au rezultat la
masurarile repetate ale marimii X.
a sirului de
valori X1, X2, . Xn care au rezultat la
masurarile repetate ale marimii X.
Precizia
de masurare a unei marimi poate fi evaluata prin mai multi indicatori
denumiti indici ai preciziei de masurare. Acesti indici sunt:
- eroarea
medie patratica sau eroarea standard, care este definita de relatia:
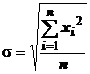 (20)
(20)
in
care xi este abaterea de la media aritmetica 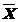 a valorilor Xi
rezultate la masurari, fiind exprimata de relatia:
a valorilor Xi
rezultate la masurari, fiind exprimata de relatia:
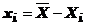 (21)
(21)
similara
relatiei (1);
- eroarea
probabila p, a carei marime se determina cu relatia:
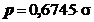 (22)
(22)
- eroarea
medie absoluta, care se poate calcula cu relatia:
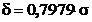 (23)
(23)
- masura
(modulul) preciziei h (sau inversul acestuia ), a carei marime rezultata din
relatia (18) este:
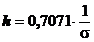 (24)
(24)
Dintre
acesti indici ai preciziei de masurare, la prelucrarea datelor
experimentale, in mod curent este folosita eroarea medie patratica, patratul
acestei marimi reprezentand dispersia erorilor.
Curba
de repartitie este totdeauna situata deasupra axei abscisei si
simetrica fata de axa ordonatelor. Suprafata cuprinsa in intervalul
curbei de repartitie ramane totdeauna egala cu unitatea si de aceea
aplatisarea curbei este conditionata de marimea dispersiei rezultatelor
obtinute la masurari. In figura 62 sunt reprezentate trei curbe de
repartitie, corespunzand parametrilor:
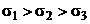
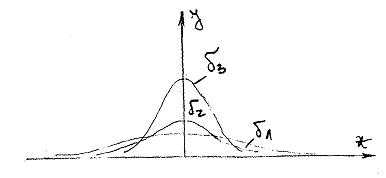
Fig. 62 - Amplitudinea curbelor de distributie normale in
functie de s
Cunoasterea
erorii medii patratice s permite determinarea campului de imprastiere a marimilor
experimentale, care este 6s (vezi fig. 3), in care sunt cuprinse peste 90% din valorile marimii
masurate experimental.
De
asemenea, cunoscandu-se eroarea medie patratica s si eroarea 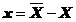 , a unei masurari X efectuate in procesul experimental, se
poate determina probabilitatea de aparitie a acestei erori respectiv a
valorii corespunzatoare marimii masurate.
, a unei masurari X efectuate in procesul experimental, se
poate determina probabilitatea de aparitie a acestei erori respectiv a
valorii corespunzatoare marimii masurate.
Astfel,
probabilitatea ca o eroare intamplatoare x sa fie cuprinsa in intervalul (x1,
x2) este exprimata, avand in vedere relatia (19) sub forma:
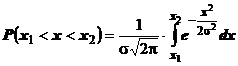 (25)
(25)
sau sub forma:
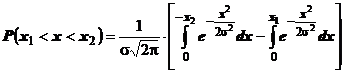
Efectuand
schimbarea de variabila 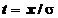 , se obtine:
, se obtine:
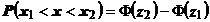 (26)
(26)
unde:
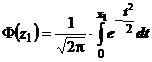
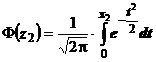
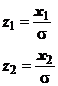
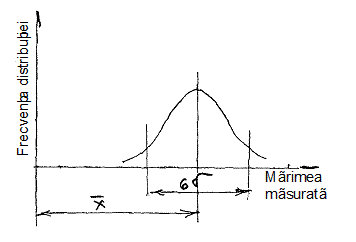
Fig. 3 - Campul de imprastiere a marimilor a caror medie este 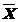 .
.
Daca
intervalul considerat este simetric fata de originea sistemului de axe,
relatia (26) devine:
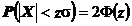 (27)
(27)
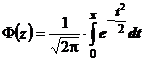 (28)
(28)
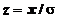
Valorile
functiei (28) sunt calculate si date in tabele.
In
consecinta, daca pentru un sir de date experimentale, rezultate la
masurarea repetata, in aceleasi conditii, a marimii respective, de un
numar determinat n de ori, s-au calculat valoarea probabil adevarata 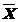 si eroarea medie
patratica s se poate
determina probabilitatea de aparitie a unei marimi individuale oarecare X,
procedandu-se astfel:
si eroarea medie
patratica s se poate
determina probabilitatea de aparitie a unei marimi individuale oarecare X,
procedandu-se astfel:
se
calculeaza raportul: 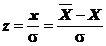 ;
;
se determina
probabilitatea de aparitie a valorii respective, din tabelul functiei
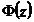 .
.
Cunoasterea
probabilitatii de aparitie a unei anumite valori a marimii masurate
are o importanta deosebita in multe din cercetarile experimentale din
domeniul metalurgiei.
Media si indicii de precizie ai masurarilor
ponderate
In
cele prezentate in acest subcapitol s-a presupus ca masurarile repetate se
executa in aceleasi conditii de precizie ale procesului experimental,
asa cum s-a precizat de la inceput si deci toate masurarile
independente sunt la fel de sigure.
In
cercetarile experimentale pot exista cazuri cand unele masurari dintr-un grup
pot fi mai sigure decat altele din diferite cauze. In aceste cazuri se acorda
ponderi diferite masurarilor individuale.
De
obicei astfel de ponderi se acorda in mod arbitrar. Se recomanda insa ca
atribuirea ponderilor sa se faca pe baza unui criteriu stiintific, ca de
exemplu pe baza legii de variatie a marimii care influenteaza asupra
sigurantei masurarilor - cand aceasta lege este cunoscuta - sau pe baza
unui anumit plat stabilit rational, verificat si corectat eventual in
timpul probelor preliminare experimentarilor sau ulterior.
Pentru
calculul mediei 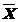 si a erorii
standard s se presupune ca o
masurare individuala X1, avand ponderea w1, este
echivalenta cu w1 masurari cu ponderi egale cu unitatea
si a caror medie este X1. Deci aceste w1 masurari nu
sunt presupuse individual egale cu X1, ci numai media lor este X1.
si a erorii
standard s se presupune ca o
masurare individuala X1, avand ponderea w1, este
echivalenta cu w1 masurari cu ponderi egale cu unitatea
si a caror medie este X1. Deci aceste w1 masurari nu
sunt presupuse individual egale cu X1, ci numai media lor este X1.
Pe
baza acestei consideratii, daca X1, X2, . Xn
este un sir de masurari avand ponderile w1, w2, . , wn,
acesta este echivalent cu w1, w2, . , wn
masurari de egala precizie.
Media
acestui nou sir, deci limita masurarilor cu ponderi diferite este:
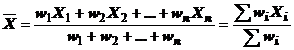 (29)
(29)
iar
eroarea medie patratica este:
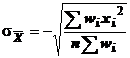 (30)
(30)
METODE DE
MASURAREA DEBITELOR, CANTITATILOR SI NIVELELOR
Generalitati
In practica determinarea
experimentala a cantitatilor de fluide existente (in recipient, pe traseu
- canale si conducte) precum si a nivelurilor de lichide, permite efectuarea
in orice moment a bilanturilor masice sau energetice a utilajelor ce compun
diversele instalatii industriale, permit controlul desfasurarii
diferitelor procese tehnologice complexe.
Mijloacele de masurare a
debitelorsi cantitatilor se intalnesc in orice ramura
industriala, la baza cercetarii experimentale a performantelor instalatiilor
energetice stand metodele bilanturilor masice si de energie.
Masurarea se refera, in general
la determinarea cantitatilor si debitelor de lichide, gaze,
combustibil etc., ce curg prin conducte
si canale.
Prin debit se intelege
volumul sau cantitatea de fluid ce trece printr-o sectiune in unitatea de
timp.
Daca Wn este
componenta vitezei pe directia normalei la elementul de suprafata dA,
al sectiunii de scurgere, in sesnul de curgere ales, debitul volumic V se
exprima cu relatia:
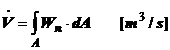 (1.3.)
(1.3.)
debitul
masic corespunzator devine:
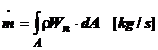 (1.4.)
(1.4.)
in
care: r este densitatea
fluidului
Vitezele locale ale
fluidului se determina experimental cu aparate, amplasate in diverse puncte ale
sectiunii de curgere, definindu-se o viteza medie pe sectiune.
Aparatele utilizate in
acest scop permit determinarea vitezei locale prin masurarea presiunii dinamice
sau utilizand efecte electrice (anemometru cu fir cald), fie alte procedee
cunoscute din literatura de specialitate.
Viteza medie pe
sectiune se va determina din relatia:
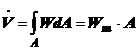 (1.5.)
(1.5.)
in
care s-a notat Wn prin W rezultand:
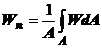 (1.6.)
(1.6.)
Masurarea debitului
volumic se poate face cu cantare de debit si prin masurarea vitezei medii
a fluidului.
Contoarele volumice
masoara cantitatea de fluid scursa intr-un interval de timp pe baza umplerii
si golirii succesive a unui volum constant, putand fi contoare de debit cu
rotoare tip Roots, eliptice, cu membrana etc. Aceste contoare de dislocare au
avantajul ca permit masurarea debitelor in regim pulsatoriu, nefiind necesare
amenajari speciale.
Determinarea debitului
volumic cu ajutorul vitezei medii presupune determinarea prin diverse metode, a
vitezei medii in conducta (canal) una din metode fiind cea care va fi
prezentata in continuare.
1.1 Metoda grafo-analitica de calcul a vitezei medii
in conducte. In conductele
circulare (fig 1.1) viteza medie se determina tinand seama de masurarile
locale de viteza, prelucrate grafo-analitic.
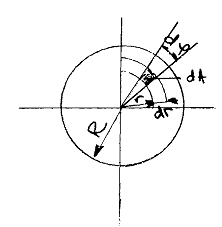
Fig.
1.1.
In
baza masurilor de viteza efectuate dupa directia radiala, exprimand:
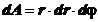
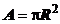 , rezulta
, rezulta
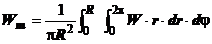 (1.5)
(1.5)
Aceasta
metoda este laborioasa. Pentru a interpreta rezultatele masuratorilor se impune
o simplificare in sensul admiterii unui camp de viteze cu simetrie radiala.
In
aceste conditii, se poate obtine o alta relatie:
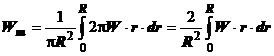 (1.6)
(1.6)
sau
schimband variabila de sub integrala:
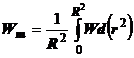 (1.7)
(1.7)
In practica masurarea vitezelor se face pe
directia diametrelor, ecuatia (1.6) scriindu-se:
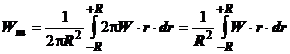 (1.8)
(1.8)
sau
 (1.9)
(1.9)
Analiza
rezultatelor experimetale se face utilizand ambele integrale:
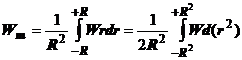 (1.10)
(1.10)
Prin acest procedeu rezulta doua functii:
 (1.11)
(1.11)
care
vor servi in calculul grafo-analitic de determinare a vitezei medii si a
debitului. Cele doua functii se traseaza prin puncte pe lungimea
diametrului, pe baza vitezelor masurate, suprafetele astfel obtinute
(fig 1.2) se raporteaza la R2, respectiv la 2R2.
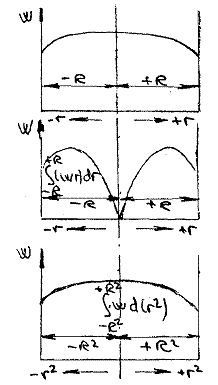
Fig. 1.2.
In aceste determinari se
va lua in considerare scara diagramei. Pentru controlul rezultatelor masurarii
se recomanda a se calcula viteza medie prin ambele metode, rezultatele nu vor
diferi cu mai mult de
1%.
De asemenea, pentru
conducte circulare de diametru mare, se recomanda sa se efectueze masurari de
viteza de-a lungul a trei diametre.
Determinarea ariilor limitate de curbele trasate grafic se face
utilizand planimetru polar.
Constructia tuburilor
pneumatice folosite la determinarea vitezelor locale face obiectul altei
discipline si anume cea hidromecanica.
2.2.
Masurarea debitului utilizand dispozitive de strangulare
Aceste masuratori se
efectueaza in conformitate cu STAS 7347-79, care corespunde integral
recomandarii ISOR 541-1967.
Metoda consta in montarea
pe o conducta a unui dispozitiv de strangulare (diafragma, ajutaj sau tub
Venturi), principiul de masurare fiind transformarea partiala a energiei
potentiale a fluidului in energie cinetica, drept consecinta viteza
in sectiunea strangulata va creste, iar presiunea va scade
fata de o sectiune din amonte de strangulare. In acest fel intre
viteza, respectiv debitul de fluid si caderea de presiune se
stabileste o relatie, folosita la masurarea indirecta a debitului.
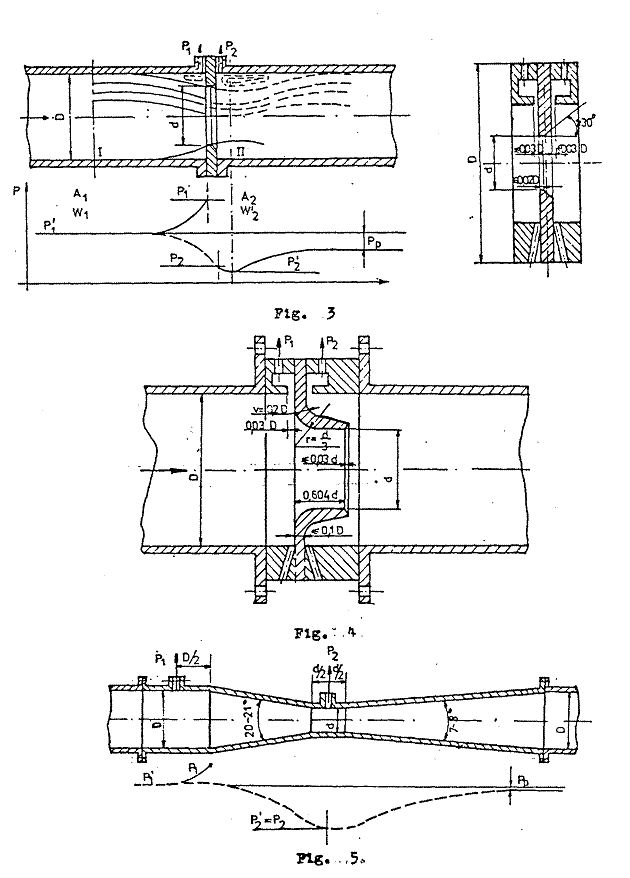
Principiul masurarii debitului
cu diagrama, ajutajul si tubul Venturi, este redat in figurile
3, 4 si 5.
Pe baza transformarii
energetice, utilizand legea lui Bernoulli, se poate determina viteza in
sectiunea strangulata a fluidului, pe baza diferentei
presiunilor de pe fata si spatele diafragmei sau ajutajului.
Diafragma, constituita
dintr-un disc de o'el metal intre doua flanse, este mai simpla in
comparatie cu ajutajele si tuburile Venturi.
Dimensiunile diafragmei
sunt de asemenea mai reduse, dar in comparatie cu ajutajul si tubul
Venturi, diafragma introduce o pierdere importanta de energie, transformata
partial in caldura.
Pierderea de presiune,
exprimata in procente din caderea de presiune cu o functie de raportul m=d2/D2.
pentru
diafragme (1), ajutaje (2) si tuburi Venturi (3) se prezinta in figura 6.
Dupa cum rezulta din fig.6 pierderea de presiune este mai mare la diafragme,
datorita muchiei ascutite a discului diafragmei si caderii bruste
de presiune.
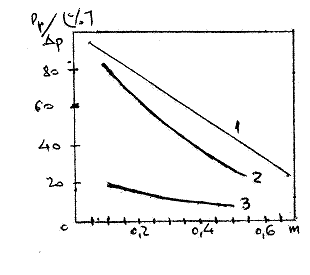
Fig. 6
La
ajutaje si tuburi Venturi o parte din energia cinetica este retransformata
in energie potentiala fapt pentru care pierderile de presiune Pp
sunt mai reduse.
2.2.1. Ecuatia de calcul a debitului
a)
Cazul
fluidelor practic incompresibile
In figurile 3, 4 si 5 s-au facut notatiile:
D - diametrul conductei;
d - diametrul sectiunii minime a dispozitivului.
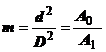 raportul sectiunilor,
sau raport de deschidere
raportul sectiunilor,
sau raport de deschidere
p'1, W1 - presiunea statica si viteza in
sectiunea amonte de dispozitiv;
p'2, W2 - presiunea statica si viteza in
sectiunea contractata a jetului de fluid, la o distanta oarecare de
dispozitiv.
In
cazul unei curgeri fara frecari, ecuatia lui Bernoulli este:
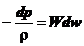 (1.12)
(1.12)
si
din ecuatia continuitatii pentru fluide incompresibile:
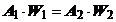 rezulta:
rezulta:
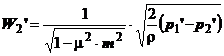 (1.13)
(1.13)
unde:
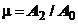 este coeficientul de
contractie a jetului;
este coeficientul de
contractie a jetului;
A2
- sectiunea contractata;
W'2'
- viteza in sectiunea contractata, reprezentand viteza teoretica, in
curgerea fara frecare.
Viteza
reala a fluidului este data de relatia
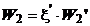 (1.14)
(1.14)
unde:
x este coeficient de viteza.
In practica este imposibil sa se masoare diferenta de presiune p'1
- p'2, putandu-se masura diferenta de presiune
p1 - p2, pe fetele amonte si aval ale
diafragmei si ajutajului.
In aceste conditii, din expresiile vitezei reale se poate scrie:
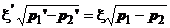 (1.15)
(1.15)
cu care debitul volumetric devine:
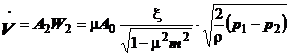 (1.16)
(1.16)
in care si si nu pot fi determinati in mod
independent, fiind functie de o serie de factori, cum sunt: forma si
marimea strangularii, calitatea suprafetelor, frecari, forma
muchiilor, pozitia prizelor de presiune etc.
Astfel termenul care cuprinde cele doua marimi, se noteaza:
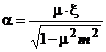 (1.17)
(1.17)
numindu-se coeficient de debit.
Formulele de calcul ale debitului volumic si masic, devin:
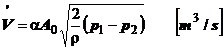 (1.18)
(1.18)
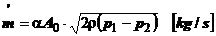 (1.19)
(1.19)
Coeficientul
de debit depinde de densitatea fluidului, de vascozitatea sa, de viteza
fluidului si marimea orificiului dispozitivului de strangulare,
rugozitatea peretilor conductei, in general putandu-se scrie:
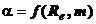 (1.20)
(1.20)
unde:
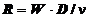 este valoarea
criteriului Reynolds.
este valoarea
criteriului Reynolds.
Modul
de calcul si factorii care determina valoarea coeficientului de debit sunt
prezentate in continuare in subcapitolul 1.2.4.
b)
Cazul
fluidelor compresibile
La masurarea debitului de
gaze sau vapori, la stabilirea ecuatiei de calcul a debitului se ia in
considerare variatia densitatii, ca urmare a caderii de presiune pe
dispozitivul de strangulare.
Admitand ipoteza ca la curgerea prin dispozitiv fluidul isi
modifica starea dupa o adiabata (fara schimb de caldura), se poate scrie:
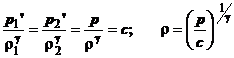 (1.21)
(1.21)
si folosind ecuatia
curgerii si a continuitatii:
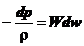 (1.22)
(1.22)
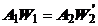
unde: g reprezinta
coeficientul adiabatic,
rezulta:
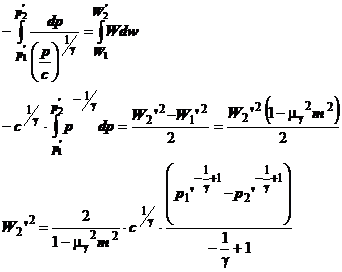
Considerand ecuatia adiabatei rezulta:
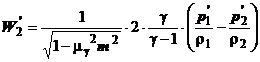 (1.23)
(1.23)
unde
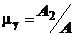 reprezinta
coeficientul de contractie a fluidului compresibil.
reprezinta
coeficientul de contractie a fluidului compresibil.
Viteza reala in sectiunea
contractata rezulta:
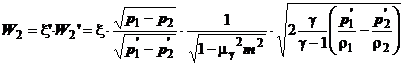
iar debitul volumic:
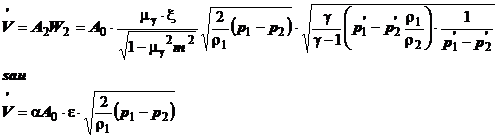 (1.24)
(1.24)
in care
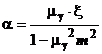 (1.25)
(1.25)
iar
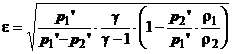 (1.26)
(1.26)
reprezinta coeficientul de expansiune.
Coeficientul de expansiune e, caracteristic fluidelor compresibile, ia in
considerare comportarea diferita a gazelor sau vaporilor fata de lichide,
care fiind practic incompresibile se caracterizeaza prin e
Influenta coeficientului e este cu atat mai mare cu cat caderea de
presiune pe dispozitiv este mai mare, sau cu cat raportul 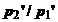 este mai mic.
este mai mic.
De
asemenea coeficientul de expansiune depinde de natura fluidului prin exponentul
adiabatic g
si de marimea orificiului, putandu-se defini prin ecuatia functionala:
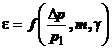 (1.27)
(1.27)



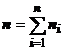
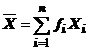
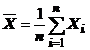
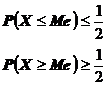
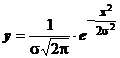
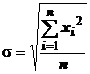

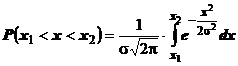
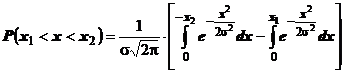
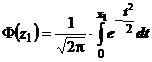
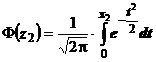
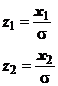

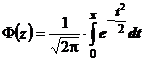
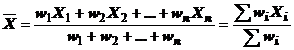
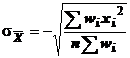
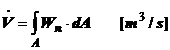
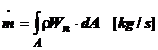
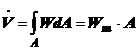

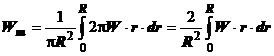
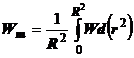
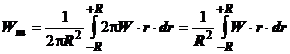 (1.8)
(1.8) (1.9)
(1.9)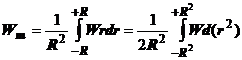 (1.10)
(1.10)

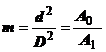
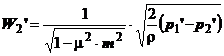
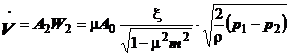 (1.16)
(1.16)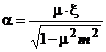 (1.17)
(1.17)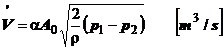 (1.18)
(1.18)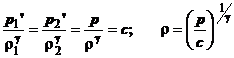 (1.21)
(1.21)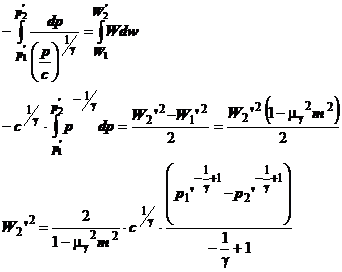
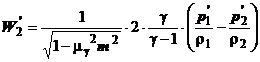
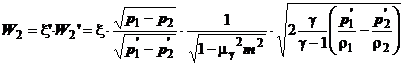
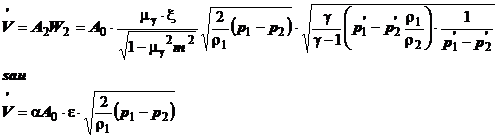 (1.24)
(1.24)