Definitia. 1.
Fie V un spatiu vectorial Euclidian. Vectorii x,y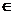 V se numesc ortogonali
daca produsul lor scalar este nul. O
submultime S V se numesc ortogonali
daca produsul lor scalar este nul. O
submultime S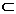 V se numeste ortogonala daca vectorii sai sunt ortogonali doi cate doi, adica <v,w>=0, V se numeste ortogonala daca vectorii sai sunt ortogonali doi cate doi, adica <v,w>=0,
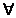 v,w v,w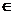 S, v S, v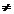 w. O multime ortogonala se numeste ortonormata daca
fiecare element al sau are norma egala cu unitatea. w. O multime ortogonala se numeste ortonormata daca
fiecare element al sau are norma egala cu unitatea.
Propozitia
2 Fie E o multime ortogonala dintr-un spatiu euclidian V
formata
din elemente nenule. Multimea E
este liniar independenta. Daca in plus, dimV=n, atunci orice multime ortogonala care contine
n elemente nenule este o baza a lui V.
Fie
V un spatiu
vectorial Euclidian si B=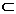 V o baza in V. B este ortonormata daca si numai daca: <ei, ej>= V o baza in V. B este ortonormata daca si numai daca: <ei, ej>=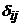 , adica 1 daca
i=j sau 0, altfel, , adica 1 daca
i=j sau 0, altfel,
unde simbolul 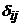 se numeste simbolul lui Kronecker. se numeste simbolul lui Kronecker.
Propozitia 3. Fie V un spatiu Euclidian cu dimV=n. Daca B= este o baza ortogonala a lui V
si v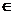 V cu v= V cu v=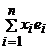 , atunci avem ca: xi=<v,ei>
/ <ei, ei>. , atunci avem ca: xi=<v,ei>
/ <ei, ei>.
In particular, daca B este o baza ortonormata, atunci xi
= <v, ei>.
Coordonatele xi=<v, ei>, i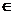 =, ale
vectorului v se numesc coordonate
euclidiene. =, ale
vectorului v se numesc coordonate
euclidiene.
Definitia 4. Fie V un spatiu vectorial Euclidian. Fie v,w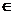 V, v,w V, v,w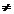 0. Vectorul 0. Vectorul 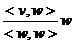 se numeste proiectia
vectorului v pe w iar numarul se numeste proiectia
vectorului v pe w iar numarul 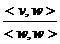 se numeste marimea algebrica a proiectiei vectorului v pe w. se numeste marimea algebrica a proiectiei vectorului v pe w.
Propozitia 5. Daca V este un spatiu vectorial Euclidian complex de dimensiune n
si B= este
o baza ortonormata, atunci <v,w>=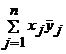 , unde xj=<v,ej>,
yj=<w,ej>. In particular, ||v||2 = , unde xj=<v,ej>,
yj=<w,ej>. In particular, ||v||2 = 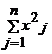 . .
Propozitia 6. Fie V
un spatiu Euclidian si W o submultime
nevida a sa. Multimea este subspatiu vectorial al lui V.
Propozitia 7. Fie V
un spatiu vectorial Euclidian de dimensiune n. Exista in V o baza
ortonormata B= .
|


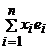 , atunci avem ca: xi=<v,ei>
/ <ei, ei>.
, atunci avem ca: xi=<v,ei>
/ <ei, ei>. 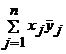 , unde xj=<v,ej>,
yj=<w,ej>. In particular, ||v||2 =
, unde xj=<v,ej>,
yj=<w,ej>. In particular, ||v||2 = 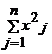 .
.