Alternativa Fredholm pentru ecuati de tip Fredholm
Vom considera din nou ecuatia (1).
Deoarece operatorul (2) este compact
pentru ecuatia (3) este adevarata alternativa Fredholm. Aceasta
conduce la urmatorul rezultat privind ecuatia (1)
Teorema V.3.1. Sau ecuatia (1) are o solutie
continua unica oricare ar fi functia continua 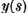 sau ecuatia
sau ecuatia
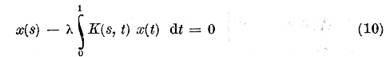
are un numar infinit de
solutii liniar independente 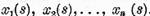 In aceaste conditii ecuatia
In aceaste conditii ecuatia
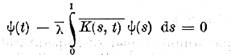
are de asemenea n solutii
continue liniar independente 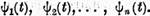 In acest caz ecuatia (1) are solutie
daca si numai daca
In acest caz ecuatia (1) are solutie
daca si numai daca
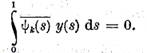
Valorile 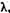 pentru care ecuatia (10) admite
solutii nenule se numesc valori caracteristice ale ecuatiei (1) sau
ale nucleului
pentru care ecuatia (10) admite
solutii nenule se numesc valori caracteristice ale ecuatiei (1) sau
ale nucleului 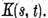 Astfel spus valorile caracteristice ale
ecuatiei (1) nu sunt altceva decat valori caracteristice ale operatorului
U . Ca urmare pentru cea mai mica in modul valoare caracteristica a
ecuatiei integrale este adevarata estimarea
Astfel spus valorile caracteristice ale
ecuatiei (1) nu sunt altceva decat valori caracteristice ale operatorului
U . Ca urmare pentru cea mai mica in modul valoare caracteristica a
ecuatiei integrale este adevarata estimarea
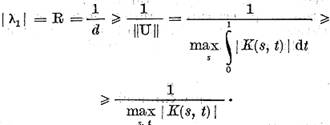
Utilizand dependenta de 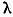 a solutiei ecuatiei 3 pe baza
teoremei III.5.2 obtinem urmatorul rezultat.
a solutiei ecuatiei 3 pe baza
teoremei III.5.2 obtinem urmatorul rezultat.
Teorema V.3.2. Intr-o vecinatate a unei valori caracteristice 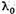 solutia ecuatiei (1) poate fi reprezentata sub forma
solutia ecuatiei (1) poate fi reprezentata sub forma
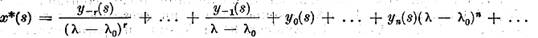
unde 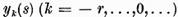 sunt functii ce depind numai de y. Seria
din membrul drept converge uniform in raport cu
sunt functii ce depind numai de y. Seria
din membrul drept converge uniform in raport cu 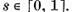
In acest mod 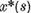 este pentru orice valoare fixa a lui s o
functie meromorfa de
este pentru orice valoare fixa a lui s o
functie meromorfa de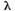 cu poli in
valorile caracteristice
cu poli in
valorile caracteristice
Vom considera spatiul 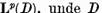 este un domeniu
marginit in spatiul n dimensional si ecuatia integrala
este un domeniu
marginit in spatiul n dimensional si ecuatia integrala
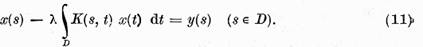
Presupunem ca nucleul 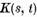 satisface
conditiile
satisface
conditiile
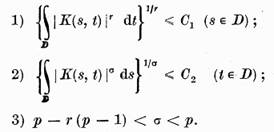
Atunci
conform teoremei amintite mai sus, operatorul intergal U cu nucleul 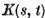 este un operator compact din
este un operator compact din 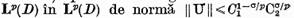 si ca urmare
a ecuatiei (11) I se aplica toate cele afirmate la relativ la
ecuatia (1). In particular daca nucleul
si ca urmare
a ecuatiei (11) I se aplica toate cele afirmate la relativ la
ecuatia (1). In particular daca nucleul 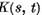 este de tip potential adica
este de tip potential adica
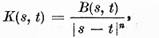
unde 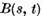 este o
functie marginita, continua pentru
este o
functie marginita, continua pentru 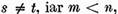 atunci conditiile enumerate mai sus sunt
indeplinite.
atunci conditiile enumerate mai sus sunt
indeplinite.
Daca in plus 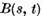 este o functie continua si
este o functie continua si
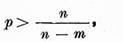
atunci operatorul U aplica 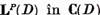 astfel ca in acest caz seriile de puteri
care reprezinta solutia
astfel ca in acest caz seriile de puteri
care reprezinta solutia 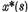 in vecinatatea valorilor caracteristice
sau vecinatatea originii converg uniform.
in vecinatatea valorilor caracteristice
sau vecinatatea originii converg uniform.


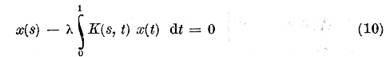
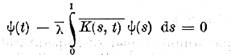
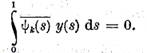
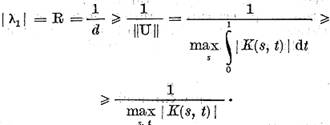
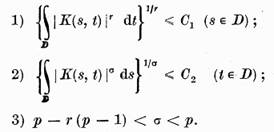
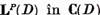 astfel ca in acest caz seriile de puteri
care reprezinta solutia
astfel ca in acest caz seriile de puteri
care reprezinta solutia