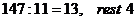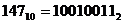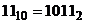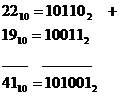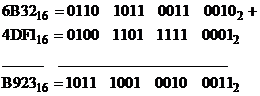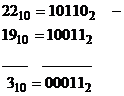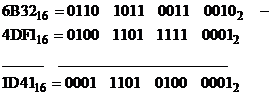 |  |
|
Operatii aritmetice cu numere fara semn
1. Adunarea
Adunarea a doua cifre in baza
q este o operatie modulo q, deci cifra cu valoarea cea mai mare va fi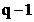 
(de exemplu, 9 in
zecimal, 1 in binar, F in hexazecimal). Daca rezultatul adunarii a
doua cifre de rang i depaseste aceasta valoare, va
apare un transport catre rangul 
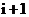, care se va aduna la suma cifrelor de rang 
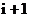. Aparitia unui transport de la cifra c.m.s. indica
o depasire a capacitatii de reprezentare a rezultatului.
In cazul adunarii binare, cifra sumei este 1 daca unul din termenii adunarii este 1. Cifra de transport este 1 numai daca ambii termeni ai adunarii sunt 1. In tabelul 2 se prezinta regula de adunare a doua cifre binare x si y.
Tabelul 2 - Adunarea a doua cifre binare
|
x |
y |
Transportul |
Suma |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exemple
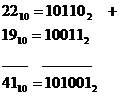
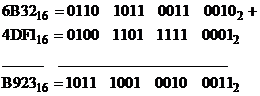
2. Scaderea
La
scaderea a doua cifre de rang i, daca cifra descazutului
este mai mica decat cifra scazatorului, apare un imprumut de la
rangul .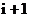
In cazul scaderii binare, diferenta este 1 daca fie descazutul, fie scazatorul este 1. Imprumutul apare numai daca descazutul este 0 si scazatorul este 1. In tabelul 3 se prezinta regula de scadere a doua cifre binare x si y.
Tabelul 3 - Scaderea a doua cifre binare
|
X |
y |
Imprumutul |
Diferenta |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exemple
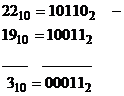
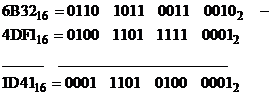
3. Inmultirea
Inmultirea se efectueaza de obicei prin adunarea repetata a unor produse partiale. La inmultirea a doua cifre binare, produsul este 1 numai daca deinmultitul si inmultitorul sunt 1. In tabelul 4 se prezinta regula de inmultire a doua cifre binare x si y.
Tabelul 4 - Inmultirea a doua cifre binare
|
x |
y |
Produsul |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exemple
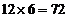
4. Impartirea
Impartirea a doua numere nu se poate efectua daca impartitorul este egal cu zero. Fiind dat deimpartitul x si impartitorul y, pentru operatia de impartire trebuie sa se determine catul Q si restul R, astfel incat sa fie satisfacuta relatia:
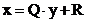
La impartirea zecimala se determina cifrele catului prin alegerea unei cifre si scaderea din restul partial (care este initial o parte a deimpartitului) a produsului dintre aceasta cifra si impartitor. Daca rezultatul scaderii este un numar pozitiv mai mic decat impartitorul, cifra aleasa este corecta. In caz contrar, se alege o alta cifra si operatia se repeta. In fiecare etapa a operatiei se obtine o cifra a catului.
In cazul impartirii binare, daca se alege in mod eronat o cifra a catului, o noua alegere nu mai este necesara, existand numai doua cifre. Operatia de impartire se va reduce la o serie de scaderi ale impartitorului din restul partial, care se efectueaza numai daca restul partial este mai mare decat impartitorul, caz in care cifra catului este 1; in caz contrar, cifra corespunzatoare a catului este 0.
Exemple
Acest document nu se poate descarca
| E posibil sa te intereseze alte documente despre: |
| Copyright © 2025 - Toate drepturile rezervate QReferat.com | Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site. { Home } { Contact } { Termeni si conditii } |
Documente similare:
|
Cauta document |