Metoda "branch and bound"

Descrierea metodei

Metoda se aplica la probleme de forma urmatoare:

Se dau multimile S₁,S₂..S_n.

Sa se determine x = (x₁,x₂,x_n) I S₁ S₂ S₃ . . S_n (sp. de solutii) care satisface P(x₁,x₂,.x_n)

-maxim

-minim

-conditii booleene

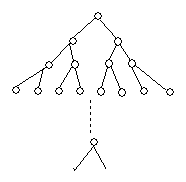
Spatiul solutiilor se organizeaza sub forma unui arbore Atunci cind arborele se genereaza prin tehnica parcurgerii in adincime - backtrack

Cind generarea nodurilor se face prin traversare in latime (sau traversarea D) - branch and bourd. Conform acestei tehnici pentru nodul viu x care este E-nodul curent , se genereaza toate nodurile (descendenti) si se depun in lista de noduri vii dupa care se trece la urmatorul E-nod care se alege din lista nodurilor vii. Daca aceasta lista e o coada , avem de-a face cu o traversare in latime; daca lista se organizeaza ca stiva , avem de-a face cu o traversare D.

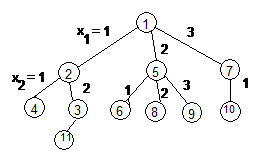
Ex. DFS 1,2,4,3,11,5,6,8,9,7,10;

BFS 1,2,5,7,4,3,6,8,9,10,11;

D 1,7,10,5,9,8,6,2,3,11,4.

T(x₁,x₂,.x_i) = numarul de valori posibile pentru x_i+1 (restrictiva explicita )

B_i+1(x₁,x₂,x_i) = predicatul de marginire derivat din T (restricta implicita.)

Aceste concepte nu se mai pot folosi in traversarile BFS, D. Branch and Bound numeste de fapt toate tehnicile care au in comun faptul ca in E-nodul curent se genereaza toate nodurile descendentilor dupa care se alege urmatorul E-nod ,dupa o strategie oarecare.

Deoarece arborele sp. de solutii este foarte mare sau chiar infinit ,aceasta strategie trebuie sa contina elementele care sa limiteze cautarea .

Ex. Problema celor 4 dame

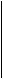x₁

x₂

x₃

x₄

Arborele FIFO Branch and Bound:

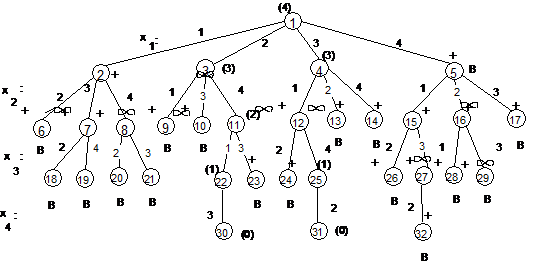
- Se observa ca backtracking lucreaza mai eficient ca spatiu

- In cazul banch-and-bound (BB) se pastreaza o coada de situatii destul de mari

- Se sugereaza determinarea unei functii care sa dirijeze cautarea (o strategie FIFO)

Printr-un calcul suplimentar sa presupunem ca se poate calcula pt. fiecare nod x o functie cost c(x).

Ex.: c(x)=lungimea dr. minim de la x la un nod solutie din subarborele de rad.x.

Folosind functia c(x) , se poate genera arborele intr-un mod dirijat.

Aceasta functie c (ideala) este greu de determinat . Se lucreaza cu o estimare a acestei functii - c* si de obicei c*(C^*(x) = f(h(x)) + g*(x) unde

h(x) =costul drumului de la rad. la x (ex.- lg. drumului)

f - o functie oarecare

g*(x) = costul estimat atingerii unui nod solutie pornind din x

Strategia BFS se obtine pt. f(h(x))=level(x) si g* =0

Strategia D se obtine pt. f(h(x))=0 si g* o functie care asigura g*(y) = min - 1

z I lista noduri vii

In plus , se asigura ca c*(x) c(x) , x - un nod.

Aceasta metoda de cautare (dupa c*(x) = f(h(x)) + g*(x)) , se numeste cautare LC (least cost) si este un prim criteriu care intervine in metoda BB (branch-and-bound). Pentru problema damelor - dificil de pus in evidenta o estimare eficienta.

Ex. 15-puzzle

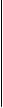
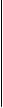
1 3 4 5 1 2 3 4

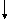
6 2 7 5 6 7 8

8 9 10 12 9 10 11 12

11 13 14 15 13 14 15

Spatiul solutiilor contine 16! combinatii ( daca nu se verifica ciclitatile)

In plus, intereseaza modul de obtinere a solutilor ,adica drumul de la radacina la solutia finala.

Pentru o pozitie data se poate decide daca pozitia are solutie (poate conduce la pozitia finala), ori nu.

Se defineste o ordine a locatiilor in patrat anume:

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

In fapt, o configuratie este o aplicatie injectiva:

poz:

piatra libera

poz (x) = i - piatra notata cu nr. x se afla pe pozita i ; in exemplul anterior poz(3)=2, poz(16)=7 etc.

Pentru fiecare configuratie si pt. orice pietricica de valoare (i) se defineste

least(i)=||

Ex. anterior : least(6)=1 least(7)=0 least (16 ) =9

Teorema: Pentru o configuratie data exista un sir de transformari pina la configuratia scop ddaca S=+p=nr.par

unde p se calculeaza astfel:

fie i, j I-linia si coloana unde este plasat spatiul liber (piatra nr.16):

p = 0, daca i+j - par (pozitia alba)

= 1, daca i+j - impar (pozitia hasurata)

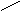
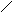
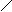
Demonstratie: Pentru configuratia scop I : S(I)=0+0 - par

Fie o configuratie T pentru care S(T) = nr. par si T` obtinut din T prin una din mutarile permise

Caz.1:

T T`

p_T`=(p_T+1)mod 2

least_T`(16)=least_T(16)-1 T

least_T`(i)=least_T(i) i

Rezulta S(T`) - nr.par.

Caz.2

Similar cazului 1

T T`

Caz.3

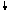
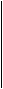
x k x

y z k y z

T T`

p_T` = (p_T+1) mod.2  (*)

least_{T '} (16)=least_T (16)-4 (**) ( 3 casute de la (i,j) la (i+1,j)

Fie x,y,z, placutele pentru pozitia initiala a lui k si cea finala :

- avem situatiile :

a) k<x k schimba locul cu 16 - se scade 1 din least(x)

b) k>x se aduna 1 la least(k)

Oricum in suma totala se scade sau se aduna 1.

Obs. de mai sus este valabila pt. x,y,z ,deci la S se aduna sau se scade un nr. impar (1sau 3).Combinind cu (*) si (**), se observa ca S(T`) ramine par.

Caz.4

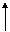
simetric cu 3

Spunem ca o configuratie T este valida ddaca un sir de transformari de la T la configuratia scop I .

Deoarece prin transformarile nu se schimba paritatea valorii S si S(I) - para TT-valida ddaca S(T) para.

Pentru acest exemplu ,vom considera:

c*(x) = f(x) + g*(x)

f(x) = level(x), iar g*(x) = nr. de placute care nu sint la locul lor.

Branch and Bound (BB) cu strategie cost minim (LC)

Modelul metodei pentru strategia LC

BB_LC (T, c*)

// cauta in arborele T al spatiului solutiilor un nod raspuns de cost minim

// e  E-nodul curent

// add(x) - depune x in lista de noduri vii

// least( ) - returneaza nodul x cu c*(x) minim din lista de noduri vii

else

for (fiecare x  descendent al lui e)

//end for

// end if (x  nod -raspuns)

eleast()

} // end while

} //end if (exista solutii)

Teorema 1 : e este un nod raspuns de cost minim

Demonstratie:

Din definitia costului estimat optimist c*, rezulta urmatoarele:

Pentru un nod raspuns r : c*(r) = c(r)

Un nod x satisface c*(x) c*(s), s fiu al lui x. Rezulta prin tranzitivitate ca c*(x) c*(d), d descendent al lui x.

Nodul e este primul nod raspuns extras din lista de noduri vii, deci celelalte noduri raspuns (daca exista) sunt in lista de noduri vii sau sunt descendenti ai unor noduri din lista de noduri vii.

Rezulta :

a.          c(e)=c*(e) c*(x), x nod din lista de noduri vii (e=least())

b.         c*(x) c*(r)=c(r), r nod raspuns descendent al lui x = nod aflat in lista de noduri vii

In consecinta c(e) c(r), r nod raspuns.

Marginire

Unele probleme ( ex: problemele de optimizare ) permit si definirea unei functii (criteriu) de marginire : c*(x) c(x) u(x); c(x) este necunoscuta.

Marginea superioara u are propietatea ca u(s) u(x), s fiu al lui x. Aceasta rezulta din structura lui u(x)=f(h(x)+k*(x) unde f si h au semnificatiile de la c* iar k* exprima o estimare supraevaluata (pesimista) a costului de la x la un nod raspuns (o solutie). Din u(s) u(x), s fiu al lui x, rezulta prin tranzitivitate ca u(d) u(x), d descendent al lui x.

Se pune problema determinarii unui nod raspuns r ( rIR=multimea nodurilor raspuns) pentru care u(r) = min.

Observatie:

Pentru un nod raspuns c*(x) c(xu(x). Deci problema determinarii lui r este echivalenta cu problema determinarii unui nod raspuns de cost minim

Modelul metodei pentru strategia LC cu marginire

BB_LC_UB (T, c*, r)

// cauta in arborele T al spatiului solutiilor un nod raspuns r cu u(r) = min

// e  E-nodul curent

// add(x) - depune x in lista de noduri vii

// least( ) - returneaza nodul x cu c*(x) minim din lista de noduri vii

;

else umin(u,ux);

}

// end for

eleast() // enull nu mai exista noduri vii

} // end while

} // end if

Teorema 2 : r este un nod raspuns pentru care u(r) = min

Demonstratie : Minimalitatea lui u(r) rezulta urmatoareale :

Deoarece u(x) c(x) c*(x) rezulta ca daca c*(x) u atunci si u(x) u. Deci este suficient sa se testeze c*(x) < u pentru a decide daca nodul x va fi generat (inserat in lista de noduri vii) ) sau nu. Aceasta conduce insa la generarea unor noduri care pot avea u(x) u deoarece c*(x) < u nu asigura u(x) < u

Atunci cind un nod rapuns este generat acesta va avea costul c*(x)=c(x)=u(x) inferior lui u deci costul sau va defini noua valoare a lui u.

Nodurile x care schimba valoarea lui u si nu sunt noduri raspuns, nu pot fi ultimele care realizeaza aceasta modificare

Demonstratie:   c*(x) u(x) < u(x) e = u, deci x este un posibil viitor E-nod (urmeaza deci si alte iteratii).

c*(y) u(y) u(x) < u(x) e = u , y descend al lui x, deci toti descendentii lui u vor fi generati deoarece u ramane neschimbat pina la terminarea executiei algoritmului. Deoarece u(x) rezulta ca printre descendentii lui x z = nod raspuns. Rezulta ca va fi generat un nod raspuns fara ca acesta sa schimbe valoarea lui u deoarece x este ultimul care a facut aceasta. (qed)

Din 1-3 rezulta ca ultimul nod raspuns retinut (r) va fi si ultimul care micsoreaza u iar alte noduri care pot micsora u nu mai exista. Rezulta ca r satisface u(r) = u = min

Problema 0/1 a rucsacului ( 0/1 knapsack

Definirea problemei Datele problemei sunt:

obiectele: i₁ i₂ i_n

greutatile: w₁ w₂ w_n

profiturile: p₁ p₂ p_n

capacitatea: M

Se cere o alegere X = ( x₁ , x₂ , , x_n ) , x_i I astfel incat

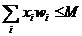(*) si

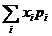- maxim (**)

o solutie admisibila satisface (*).

o solutie optima este admisibila si satisface (**)

Obs. 1. Daca 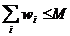solutia optimala este x_i=1, i=1, . ,n. Deci problema are sens pentru.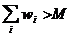

Spatiul solutilor se poate organiza sub forma unui arbore binar :

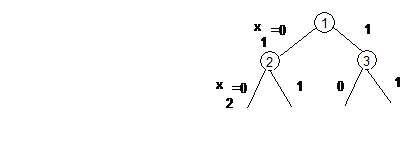
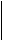x_i  0 - obiectul i se ignora

1 - obiectul i se introduce in rucsac

Nodurile raspuns sint cele care reprezinta solutii admisibile 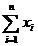w_i M

Pentru orice nod raspuns c(x) 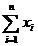 p_i

Pentru orice nod terminal care nu este nod raspuns c(x)

Pentru orice alt nod y se defineste c(y)  min

Construim doua functii : c*(x) si u(x) a.i. c*(x) c(x) u(x)

Fie x un nod de pe nivel k; valorile x₁,x₂,x_k-1 sint deja calculate.

Valorile c*(x) si u(x) pot fi calculate cu procedura urmatoare:

bound(p,w,rw,cp,n,k,c*x,ux)

// rw = capacitatea ramasa

// cp = profitul deja obtinut

// obiectele k, . ,n nu au fost inca analizate

} // end for j i+1 . ,n

// -ux profitul sigur ce se poate obtine din nodul x

return;

} // end if (c w(i))

} // end for ik, . ,n

c*x ux; // toate obiectele k,k+1, . ,n pot fi incarcate in rucsac

Algoritmul BB_LC pentru problema 0/1 a rucsacului:

Crearea si adaugarea unui nod in lista de noduri vii

newnode (nod,par,lev,t,cap,prof,cost);

// creaza un nod nou i si il adauga la lista de noduri vii

Procedura BB-LC pentru problema 0/1 a rucsacului

LC_KnapSack(p,w,M,n,s)

// p(1, . ,n) -- profiturile

// w(1, . ,n) -- greutatile

// M -- capacitatea rucsacului

// obiectele sunt ordonate astfel incit p(i)/w(i) p(i+1)/w(i+1)

// E  E-nodul curent

// r  nodul raspuns cu u(r) minim intre nodurile raspuns atinse

// least( ) -- functie ce returneaza nodul x cu c*(x) minim (profit estimat maxim), din lista de noduri vii

; // nod raspuns : c*(x)  c(x)   [prof+p(i)];

else umin(u,ux);

};

// vezi daca fiul din dreapta poate deveni viu

bound(p,w,cap,prof,n,i+1,c*x,ux);

if ( c*x < u) // fiul din dreapta devine viu

; // nod raspuns : c*(x)  c*x c(x) prof

else umin(u,ux);

}

e least(); // (enul nu mai exista noduri vii

} //end while

return(r)