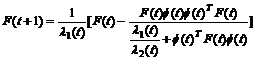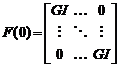Amplificarea de adaptare

Amplificarea de adaptare

Formula de reprezentare a inversei amplificarii de adaptare F(t+1)^-1, data de ecuatia (3.45), se generalizeaza prin introducerea a doi parametrii de ponderare l (t) si l (t) asa cum este indicat in continuare:

F (t+1)^-1 l (t)F(t)^-1+l (t)f(t)f(t)^T (3.49)

0<l (t)≤1; 0<l (t) <2; F(0)>0

De observat ca l (t) si l (t) in ecuatia (3.49) au un efect contrar. l (t)<1 tinde sa creasca amplificarea de adaptare (inversul amplificarii descreste), l (t) tinde sa descreasca amplificarea de adaptare (inversul amplificarii creste). Pentru fiecare alegere a parametrilor l (t) si l (t), corespunde un profil de variatie a amplificarii de adaptare si o interpretare diferentiata in termenii criteriului de eroare care este minimizat in conformitate cu AAP.

Prin utilizarea lemei de inversare matriciala data prin ecuatia (3.38), obtinem plecand de la ecuatia (3.49):

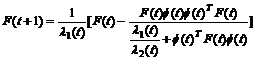(3.50)

Vom da in continuare cateva alegeri posibile pentru l (t) si l (t) si interpretarile corespunzatoare asupra calitatii algoritmului CMMPR.

C.1: Amplificare descrescatoare

In acest caz:

l (t)=l l (t)=1  (3.51)

si F(t+1)^-1 este dat de ecuatia (3.45) care conduce la o amplificare de adaptare descrescatare. Criteriul minimizat este acelasi cu cel din ecuatia (3.26). Acest tip de profil al amplificarii convine pentru identificarea sistemelor stationare.

C.2: Factor de uitare fix

In acest caz:

l (t)=l ; 0< l <1 ; l (t)=l (3.52)

Valorile tipice pentru l sunt: l

Criteriul de minimizare va fi :

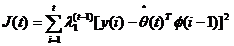
Efectul lui l <1 este de a introduce o ponderare din ce in ce mai slaba asupra datelor vechi (i<t), care merita sa fie uitate. Din acest motiv l este numit si factor de uitare. Greutatea maxima in criteriu este data de ultimul termen din suma (3.53), adica de ultima eroare de predictie. Acest tip de profil convine pentru identificarea sistemelor cu parametri lent variabili in timp.

C.3: Factor de uitare variabil

In acest caz:

l (t)=l (3.54)

si factorul de uitare l este dat de expresia,

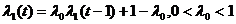  (3.55)

valorile tipice fiind :

l l

Relatia (3.51) conduce la un factor de uitare, care tinde asimtotic spre 1. Criteriul de minimizat va fi :

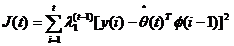(3.56)

Cum l (t) tinde la 1 pentru i mare, rezulta numai  un efect de uitare pentru datele initiale (profilul tinde spre o amplificare descrescatoare).

Acest tip de algoritm este recomandat pentru identificarea sistemelor stationare, pentru ca evita o descrestere prea rapida a profilului de adaptare si aceasta conduce in general la o accelerare a convergentei (mentinerea unei amplificari crescute cand suntem departe de optim).

C.4: Urma constanta

In acest caz, (t) si (t) sunt alese automat la fiecare pas pentru asigurarea unei urme constante a matricei de amplificare (suma constanta de termeni diagonali):

Tr F(t+1) = Tr F(t)=Tr F(0) =nGI

unde n este numarul de parametri si GI castigul initial (valorile tipice: GI=0,1 . ,4), matricea F(0) avand deci o reprezentare diagonala:

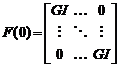(3.57)

Criteriul minimizat este de forma:

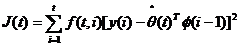(3.58)

unde f(t,i) reprezinta profilul de uitare.

Prin aceasta tehnica ne deplasam la fiecare pas in directia optima a CMMPR, dar pastram amplificarea aproape constanta.

Valorile (t) si (t) se determina pornind de la ecuatia:

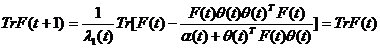(3.59)

prin fixarea raportului (t)= (t)/ (t) (ecuatia (3.59) este obtinuta din ecuatia (3.50)).

Acest tip de profil de amplificare convine pentru identificarea sistemelor cu parametri variabili in timp.

C.5: Amplificare descrescatoare si urma constanta 

In acest caz, comutam de la C.1 la C.4 cand:

TrF t)≤nG; G=0,1 . 4   (3.60)

unde, G este fixat de la inceput. Acest profil convine pentru identificarea sistemelor variabile in timp in absenta informatiilor initiale asupra parametrilor.

C.6: Factor de uitare variabil si urma constanta

In acest caz, comutam de la C.3 la C.4 cand:

TrF t)≤nG; G=0,1 . 4  (3.61)

unde, G este fixat de la inceput. Utilizarea este aceeasi ca pentru C.5.

C.7: Amplificare constanta

In acest caz:

(t)= (t)= (3.62)

si deci din ecuatia (3.49) rezulta:

F(t+1)=F(t)=F(0)   

Obtinem deci in mod evident, algoritmul de adaptare de tip gradient ameliorat dat de ecuatia (3.20) sau de ecuatia (3.24). Putem utiliza acest algoritm pentru identificarea proceselor stationare sau variabile in timp, dar cu putini parametri, si in prezenta unui nivel de zgomot scazut. Acest tip de adaptare conduce la performante inferioare celor oferite de cazurile C.1, C.2, C.3 si C.4, dar punerea sa in practica este mai simpla.

Alegerea amplificarii initiale F(0)

Amplificarea de adaptare initiala F(0) este de forma data de ecuatia (3.48) respectiv (3.52). In absenta informatiilor initiale asupra parametrilor de estimat (o valoare tipica a estimarilor initiale este egala cu 0), alegem un castig initial GI mare din motive care au fost deja explicate. O valoare tipica este GI=1000. Din contra, daca avem estimarea initiala a parametrilor (rezultati de exemplu dintr-o identificare anterioara), alegem o amplificare initiala scazuta. In general, in acest caz GI≤1.

Pe masura ce ne apropiem de estimarile corecte ale parametrilor modelului, amplificarea de adaptare scade (o masura semnificativa este urma sa); putem interpreta amplificarea de adaptare ca o masura a preciziei de estimare (sau de predictie). Aceasta explica alegerea lui F(0) propus mai sus. De notat ca in anumite ipoteze, F(t) este chiar o masura a calitatii mecanismului de estimare si prin urmare, poate da indicatii asupra evolutiei unei proceduri de estimare. Astfel, daca urma lui F(t) nu descreste semnificativ, estimarea parametrilor este in general proasta. Acest fenomen apare de exemplu cand alegerea semnalului de proba utilizat nu este cea potrivita.