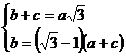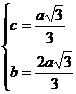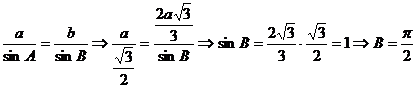Relatia
lui Van Aubel si aplicatii la rezolvarea problemelor de geometrie
Am alcatuit acest
material in urma cu 10 ani, prin toamna lui 1991 cu intentia de a-l trimite
spre publicare Gazetei Matematice. In cele din urma, m-am razgandit - nu
consideram ca este suficient de bine facut pentru a-si gasi locul acolo. Il
scot acum de la arhiva in speranta ca voi trezi interesul macar catorva
persoane pasionate ca si mine de geometria "clasica".
OBSERVATIE. La vremea
liceului (prin toamna lui 1985), dl. profesor Cristian Bosneag de la Liceul de
Informatica ne-a predat relatia de care voi vorbi in cele ce urmeaza. In
manualele de atunci, nu era cuprinsa nici macar ca exercitiu. In actualele
manuale, nu are cum, programa de geometrie fiind supraincarcata cu vectori si
geometrie analitica. Geometria "clasica" a fost izolata in clasele VI-VIII,
cand elevii abia invata sa rezolve ecuatii de gradul I. Nu sunt impotriva
geometriei analitice, dar cred ca 40 de ore in clasa a XI-a erau suficiente.
Materialul de fata se vrea o pledoarie in favoarea geometriei "clasice", prea
usor aruncata la gunoi de dragul reinnoirii programelor scolare.
Relatia lui Van Aubel
In triunghiul
oarecare ABC, se duc cevienele AA', BB' si CC', concurente in punctul I (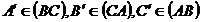 ). Are loc relatia:
). Are loc relatia:
|
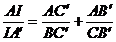 (1) (1)
|
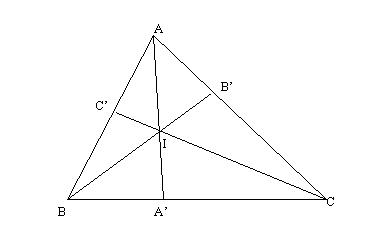
Figura 1. Relatia
lui Van Aubel
Relatia (1)
poarta numele de relatia lui Van Aubel. Sincer vorbind, nu am idee cine
a fost Van Aubel. O alta relatie descoperita de el este utila la calculul lungimii
unei ceviene plecand din varful unghiului drept intr-un triunghi dreptunghic;
aceasta din urma o puteti gasi in excelenta carte "Surprize in matematica
elementara" publicata de dr. Viorel Gh. Voda in 1981 la Ed. Albatros.
Sa revenim insa
la relatia (1). Utilitatea ei apare imediat: cu ajutorul acestei relatii
putem calcula direct raportul segmentelor determinate de punctul de intersectie
a trei ceviene pe oricare dintre ele, fara a mai recurge la teoremele lui
Menelaus sau Ceva. Relatia este de fapt un 'shortcut' extrem de util la
calculul rapoartelor sus-amintite.
Demonstratie. Scriem teorema
lui Menelaus in triunghiul AA'C intersectat de transversala BIB':
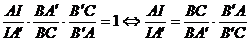 (2)
(2)
Pe de alta parte,
scriem teorema lui Ceva pentru cevienele concurente AA', BB' si CC' si rezulta:
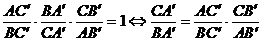
Construim
proportii derivate pentru a scoate raportul 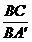 , pe care il vom inlocui apoi in relatia (2):
, pe care il vom inlocui apoi in relatia (2):
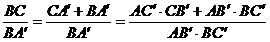
Relatia (2)
devine astfel:
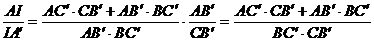
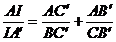 q.e.d.
q.e.d.
Problema rezolvata 1 (105/25 din [1]). Fie M si N doua
puncte situate pe laturile (AB) si (AC) ale triunghiului ABC astfel incat:
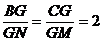
unde G este punctul de intersectie al segmentelor (BN)
si (CM). Sa se demonstreze ca 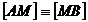 si
si  .
.
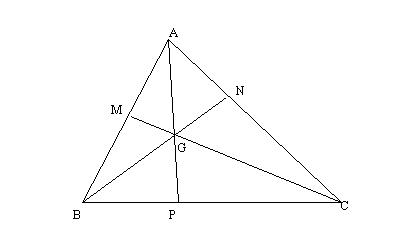
Figura
2. La problema rezolvata 1.
Solutie. Fie 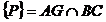 . Notam:
. Notam:
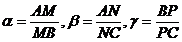
Conform teoremei lui Ceva, putem scrie:
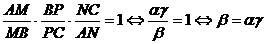 (4)
(4)
Intra acum in
scena starul serii: relatia lui Van Aubel. Conform acesteia, putem scrie:
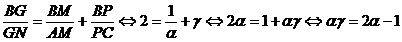 (5)
(5)
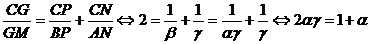 (6)
(6)
Din relatiile (5)
si (6), rezulta imediat ca 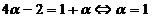 ; inlocuind aceasta valoare in relatia (6), obtinem
; inlocuind aceasta valoare in relatia (6), obtinem 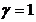 . Din relatia (4), se deduce acum imediat ca
. Din relatia (4), se deduce acum imediat ca 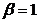 .
.
Revenind la
notatii, avem:
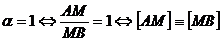
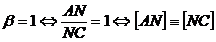 , q.e.d.
, q.e.d.
Problema rezolvata 2 (59/20 din [1]). Fie triunghiul
ABC. Consideram punctele 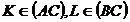 astfel incat
astfel incat 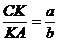 si
si 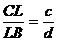 , unde
, unde 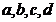 sunt numere reale pozitive. Sa se calculeze rapoartele
sunt numere reale pozitive. Sa se calculeze rapoartele 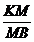 si
si 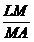 .
.
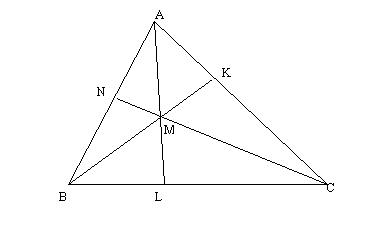
Figura
3. La problema rezolvata 2.
Solutie. Notam 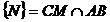 . Conform teoremei lui Ceva, avem:
. Conform teoremei lui Ceva, avem:
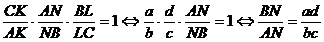 (7)
(7)
Se scriu acum relatiile lui Van Aubel:
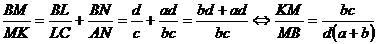 (8)
(8)
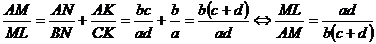 (9)
(9)
Relatiile (8) si (9) exprima chiar rezultatele cerute.
Problema rezolvata 3. (4/97 din [2]) In punctele A si B
ale unui cerc, care nu sunt diametral opuse, se duc doua tangente la cerc, care
se intalnesc in C. Prin A se duce o paralela la BC, care taie cercul in D.
Dreapta CD taie cercul in E, iar dreapta AE intersecteaza pe BC in F. Sa se
demonstreze ca:
a) 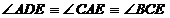
b)
Triunghiurile ACF si CEF sunt asemenea;
c) 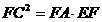
d) 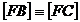
e) Sa
se determine masura unghiului 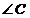 astfel incat
astfel incat 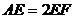 .
.
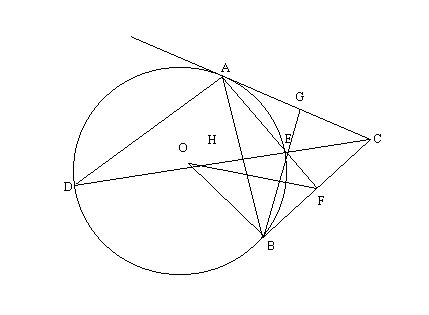
Figura 4. La problema rezolvata 3.
Solutie. Aceasta problema este se pare alcatuita de
profesorul Octavian Sacter prin anii '50; a fost subiect de admitere la zeci de
examene (mai putin punctul e), adaugat ceva mai recent; de altfel, acest punct
face legatura cu tema materialului de fata).
a) 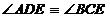 , ca alterne interne formate de dreptele AD si BC cu secanta
DC. Dar
, ca alterne interne formate de dreptele AD si BC cu secanta
DC. Dar 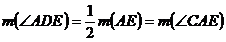
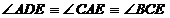 .
.
b)
Conform punctului a), cele doua triunghiuri au 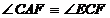 . In plus, mai avem
. In plus, mai avem 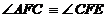 (unghi comun). Rezulta
ca ele sunt asemenea (cazul II).
(unghi comun). Rezulta
ca ele sunt asemenea (cazul II).
c)
Scriem asemanarea triunghiurilor de la punctul b):
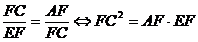
d)
Puterea lui F fata de cerc se scrie 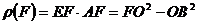 (O este centrul
cercului). Dar triunghiul OBF este dreptunghic in B, deci
(O este centrul
cercului). Dar triunghiul OBF este dreptunghic in B, deci 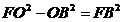 . Rezulta ca
. Rezulta ca 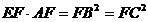 (conform punctului c)), deci
(conform punctului c)), deci 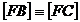 .
.
e)
Fie 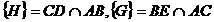 .
.
Conform
teoremei lui Ceva in triunghiul ABC pentru cevienele concurente AF, BG si CH,
avem:
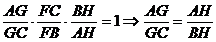 (10)
(10)
Scriem
relatia lui Van Aubel:
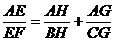
Tinem
acum cont de ipoteza 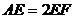 si de relatia (10).
Rezulta:
si de relatia (10).
Rezulta:
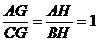 [CH] este
mediana in triunghiul ABC.
[CH] este
mediana in triunghiul ABC.
Triunghiul ABC
este isoscel (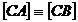 , ca tangente duse din C la cerc) mediana [CH]
este si inaltime
, ca tangente duse din C la cerc) mediana [CH]
este si inaltime 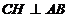 . Pe de alta parte,
. Pe de alta parte, 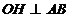 (diametrul este
perpendicular pe mijlocul coardei) punctele O, C, H sunt coliniare [ED] diametru al
cercului
(diametrul este
perpendicular pe mijlocul coardei) punctele O, C, H sunt coliniare [ED] diametru al
cercului 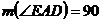 (unghiul EAD fiind
inscris in semicercul EBD)
(unghiul EAD fiind
inscris in semicercul EBD) 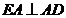 .
.
Dar 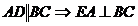 [AF] este
mediana si inaltime in triunghiul ABC
[AF] este
mediana si inaltime in triunghiul ABC 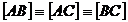 triunghiul ABC
este echilateral. Rezulta
triunghiul ABC
este echilateral. Rezulta 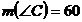 .
.
Problema rezolvata 4. Bisectoarele (AD), (BE) si (CF)
ale triunghiului ABC sunt concurente in punctul
I. Sa se arate ca daca:
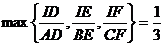 , atunci triunghiul este echilateral.
, atunci triunghiul este echilateral.
(D.M.
Batinetu-Giurgiu, Olimpiada, 1986, etapa locala)
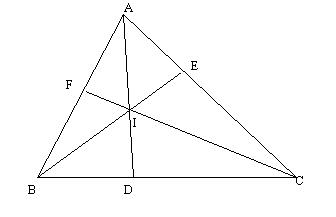
Figura 5. La problema
rezolvata 4.
Solutie. Utilizam
notatiile obisnuite pentru lungimile laturilor triunghiului dat: 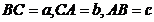 . Cunoastem de asemenea notatia
. Cunoastem de asemenea notatia 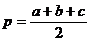 .
.
Conform teoremei bisectoarei in triunghiul ABC, putem
scrie:
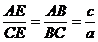
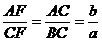
Scriem relatia lui Van Aubel:
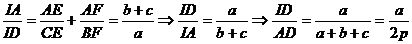
Similar, rezulta ca 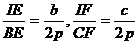 .
.
Cum 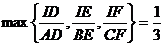 , rezulta ca au loc inegalitatile:
, rezulta ca au loc inegalitatile:
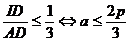
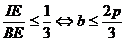
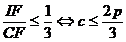
Adunand membru cele trei inegalitati, rezulta 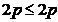 . Aceasta fiind o egalitate, toate cele trei inegalitati care
s-au adunat pentru a o obtine trebuie sa se transforme in egalitati. Rezulta
. Aceasta fiind o egalitate, toate cele trei inegalitati care
s-au adunat pentru a o obtine trebuie sa se transforme in egalitati. Rezulta 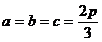 triunghiul ABC
este echilateral, q.e.d.
triunghiul ABC
este echilateral, q.e.d.
Problema rezolvata 5. (20/204 din [2]) Fie triunghiul
ABC. Unui punct M din interiorul triunghiului i se asociaza numarul real:
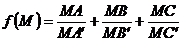
unde 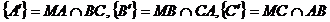 . Sa se arate ca functia
. Sa se arate ca functia 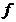 admite un minim atunci cand M coincide cu centrul de greutate
al triunghiului ABC.
admite un minim atunci cand M coincide cu centrul de greutate
al triunghiului ABC.
Solutie. Notam 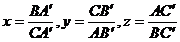 . Conform relatiei lui Van Aubel, avem:
. Conform relatiei lui Van Aubel, avem:
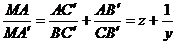
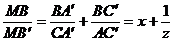
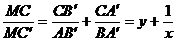
Adunand cele trei egalitati, rezulta ca
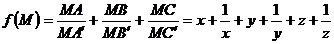
Conform
inegalitatii mediilor, avem insa 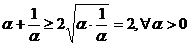 . Egalitatea are loc daca si numai daca
. Egalitatea are loc daca si numai daca 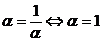 .
.
Rezulta
ca 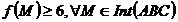 . Minimul lui
. Minimul lui 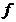 este atins cand
este atins cand 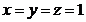 , adica atunci cand A', B' si C' sunt mijloacele laturilor
(BC), (CA) si (AB). In acest caz, M este evident centrul de greutate al
triunghiului ABC.
, adica atunci cand A', B' si C' sunt mijloacele laturilor
(BC), (CA) si (AB). In acest caz, M este evident centrul de greutate al
triunghiului ABC.
Problema rezolvata 6. Fie M un punct in interiorul
triunghiului ABC. Notam 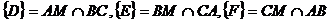 . Sa se determine minimul produsului:
. Sa se determine minimul produsului:
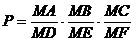
Solutie. Analog cu problema precedenta, notam:
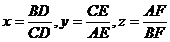
Scriem relatiile lui Van Aubel (se pare ca are multe
relatii acest domn Van Aubel J
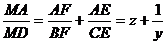
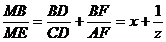
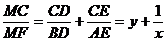
Inmultim
cele trei relatii si rezulta:
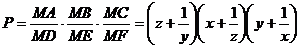 (11)
(11)
Conform inegalitatii mediilor,
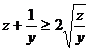 , egalitatea avand loc cand
, egalitatea avand loc cand 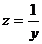
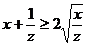 , egalitatea avand loc cand
, egalitatea avand loc cand 
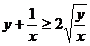 , egalitatea avand loc cand
, egalitatea avand loc cand 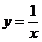 .
.
Din relatia (11) si cele trei inegalitati de mai sus,
rezulta ca:
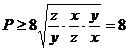 , minimul fiind atins cand:
, minimul fiind atins cand:
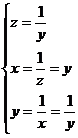
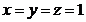 , ceea ce se intampla (vezi problema precedenta) cand M este
centrul de greutate al triunghiului ABC. Asadar, produsul P are un minim egal
cu 8 cand M=G.
, ceea ce se intampla (vezi problema precedenta) cand M este
centrul de greutate al triunghiului ABC. Asadar, produsul P are un minim egal
cu 8 cand M=G.
OBSERVATIE. La problemele 5
si 6, nu am mai desenat figurile. Acestea sunt similare cu figura 1, avand insa
numele punctelor modificate.
Problema rezolvata 7. Fie triunghiul ABC si punctele
mobile 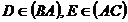 , alese astfel incat sa fie respectata conditia
, alese astfel incat sa fie respectata conditia 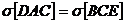 . Fie
. Fie 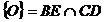 si
si 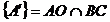 . Sa se determine valoarea minima a raportului
. Sa se determine valoarea minima a raportului 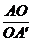 si pozitiile lui D si
E pentru care se realizeaza acest minim.
si pozitiile lui D si
E pentru care se realizeaza acest minim.
(Marius
Stanean, 20679, G.M. 2/1986)
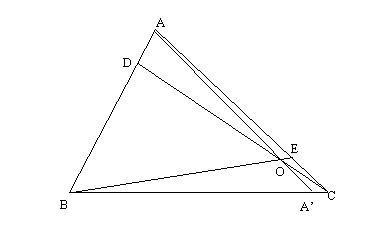
Figura 6. La problema rezolvata 7.
Solutie. Fie 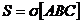 si
si 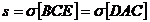 . Se duc inaltimile
. Se duc inaltimile 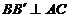 si
si 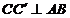 (in figura, nu le-am
mai inclus din motive de incarcare a desenului).
(in figura, nu le-am
mai inclus din motive de incarcare a desenului).
Avem: 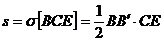
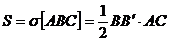
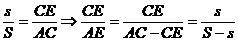 (12)
(12)
Similar se arata ca 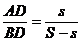 (13)
(13)
Se scrie acum relatia lui Van Aubel:
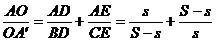
Fie 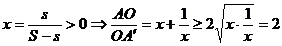 . Minimul raportului
. Minimul raportului 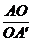 este deci egal cu 2,
fiind atins atunci cand
este deci egal cu 2,
fiind atins atunci cand 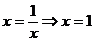 . In acest caz, rezulta din (12) si (13) ca
. In acest caz, rezulta din (12) si (13) ca 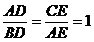 , deci D si E sunt mijloacele laturilor (AB), respectiv (AC).
, deci D si E sunt mijloacele laturilor (AB), respectiv (AC).
Problema rezolvata 8. In triunghiul ABC, bisectoarele
interioare ale unghiurilor A si B taie (BC), respectiv (AC) in M si N. Fie 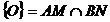 . Se cunoaste ca
. Se cunoaste ca 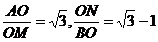 . Sa se calculeze masurile unghiurior triunghiului ABC.
. Sa se calculeze masurile unghiurior triunghiului ABC.
(Admitere,
Matematica, sesiunea speciala, 1988)
Solutie. Fie 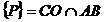 ; evident, (CP este bisectoarea unghiului C.
; evident, (CP este bisectoarea unghiului C.
Conform teoremei bisectoarei, putem scrie (cu
notatiile obisnuite intr-un triunghi, 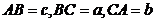 ):
):
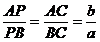 ;
; 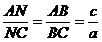 ;
; 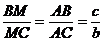 (14)
(14)
Din relatia lui Van Aubel si relatiile (14), rezulta:
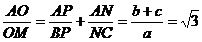
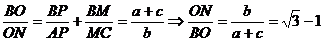
Avem deci sistemul:
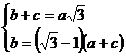
Rezolvand acest sistem (nu mai intru in detalii) se
gaseste:
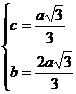
Scriem acum teorema cosinusului in triunghiul ABC:
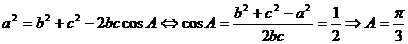
Conform teoremei sinusurilor,
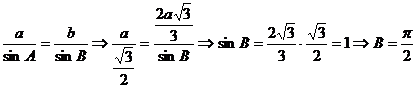
Prin diferenta, rezulta 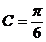 .
.
Problema rezolvata 9. Daca O este un punct in interiorul
triunghiului ABC si A', B', C' celelalte intersectii ale dreptelor OA, OB, OC
cu laturile triunghiului, sa se arate ca este adevarata relatia:
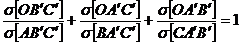
(Al.
Otet, 21215*, G.M. 9/1987)
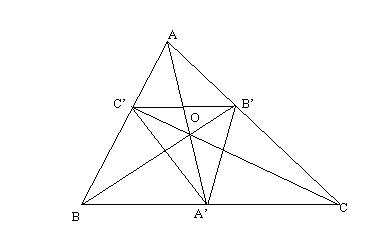
Figura 7. La problema rezolvata 9.
Solutie. Vom utiliza urmatoarea proprietate: Daca in
triunghiul ABC luam punctul 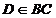 , avem:
, avem:
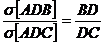 (se demonstreaza usor,
tinand seama ca triunghiurile ADB si ADC au inaltimea din A comuna).
(se demonstreaza usor,
tinand seama ca triunghiurile ADB si ADC au inaltimea din A comuna).
Sa
revenim acum la problema noastra. Notam pentru inceput rapoartele:
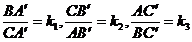
Conform
teoremei lui Ceva, avem relatia 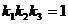 (15); din aceasta
egalitate, rezulta
(15); din aceasta
egalitate, rezulta 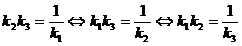 .
.
Fie 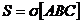 . Conform proprietatii amintite, avem:
. Conform proprietatii amintite, avem:
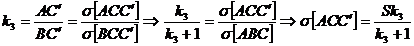 (16)
(16)
Utilizand aceeasi proprietate, rezulta si:
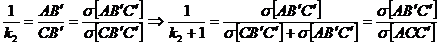
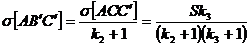 (17)
(17)
Scoatem de aici si 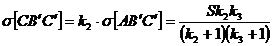 (18)
(18)
Aici intervine relatia lui Van Aubel:
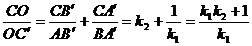 (19)
(19)
Pe de alta parte,
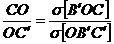 (20)
(20)
Din relatiile (19) si (20), rezulta:
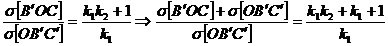
 (21)
(21)
Din relatiile (18) si (21) rezulta ca:
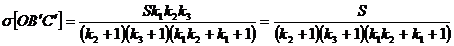 (22)
(22)
(s-a utilizat aici relatia (15)).
Se impart membru cu membru relatiile (22) si (17) si
rezulta:
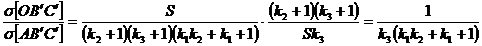
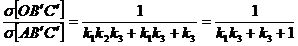 (23)
(23)
Similar, se obtin relatiile:
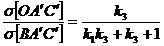 (24)
(24)
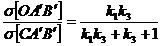 (25)
(25)
Adunand membru cu membru relatiile (23), (24) si (25),
gasim exact:
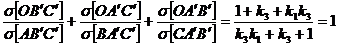 , q.e.d.
, q.e.d.
Bibliografie
- St. Ianus, N. Soare, L. Niculescu, S. Dragomir,
M. Tena - Probleme de geometrie si trigonometrie pentru clasele IX-X,
E.D.P, 1983
- D. Branzei, S. Anita, E. Onofras, Gh. Isvoranu - Bazele
rationamentului geometric, Ed. Academiei, 1983.







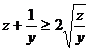 , egalitatea avand loc cand
, egalitatea avand loc cand 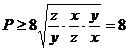 , minimul fiind atins cand:
, minimul fiind atins cand: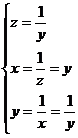

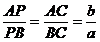 ;
;