Oscilatii
mecanice cu un singur grad de libertate
Un sistem mecanic poate sa
sufere deplasari fata de un anumit sistem de
referinta. Daca parametrii care descriu aceste deplasari se
modifica alternativ in timp in jurul valorilor corespunzatoare
starii de referinta se spune ca sistemul efectueaza
oscilatii sau vibratii.
Miscarea oscilatorie este
foarte frecventa in natura si in tehnica. Exemple de
oscilatii pot fi: deplasari ale atomilor, moleculelor retelelor
cristaline fata de pozitiile de echilibru, deplasari ale
moleculelor de aer in timpul propagarii undelor sonore, masa unui
seismograf, balansierul unui ceas, etc.
Daca toate elementele
miscarii se repeta periodic dupa un anumit interval de
timp, se spune ca oscilatiile sunt periodice. De exemplu miscarea
balansierului unui ceas este periodica. Daca elementele
miscarii unui sistem mecanic nu se repeta periodic,
miscarea oscilatorie este aperiodica. Zgomotele sau vibratiile
scoartei Pamantului in timpul unui cutremur sunt exemple de
oscilatii aperiodice.
Deplasarile sistemului
mecanic fata de starea de referinta poate fi insa
foarte complicata. Studierea acestora se face prin generalizarea
miscarii oscilatorii a unui sistem mecanic cu un grad de libertate,
adica a miscarii in care are loc modificarea in timp a unui
singur parametru (deplasare liniara, unghiulara, etc.).
In continuare se
analizeaza doar oscilatiile periodice cu un singur grad de libertate,
deoarece analiza oscilatiilor periodice cu mai multe grade de libertate
este mai dificila si depaseste scopul acestui curs.
Oscilatorul armonic liniar
Pentru analizarea miscarii oscilatorii periodice este
utila alegerea unui model care sa reflecte cat mai fidel comportarea
sistemului mecanic real. Cu cat miscarea oscilatorie este mai
complicata, cu atat modelul mecanic al miscarii va fi mai
complicat.
Cel mai simplu model de oscilator periodic, cu un grad de libertate,
este prezentat in figura 1.
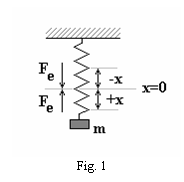 Acesta
modeleaza comportarea unui sistem alcatuit dintr-un corp de masa
m, suspendat prin intermediul unui element elastic (de exemplu un resort, de
masa neglijabila), de un reper fix. Sub actiunea
greutatii corpului, resortul se alungeste pana ajunge
intr-o pozitie de echilibru. Scotand corpul din pozitia de
echilibru prin alungirea sau comprimarea resortului, pe directie
verticala si apoi eliberand corpul, acesta va incepe sa oscileze
in jurul pozitiei de echilibru. Pozitia corpului in orice moment este
complet determinata prin abscisa x masurata de la pozitia
de echilibru x = 0. Prin conventie se considera ca axa lui x are
originea in pozitia de echilibru si sensul pozitiv indreptat in
sensul alungirii resortului.
Acesta
modeleaza comportarea unui sistem alcatuit dintr-un corp de masa
m, suspendat prin intermediul unui element elastic (de exemplu un resort, de
masa neglijabila), de un reper fix. Sub actiunea
greutatii corpului, resortul se alungeste pana ajunge
intr-o pozitie de echilibru. Scotand corpul din pozitia de
echilibru prin alungirea sau comprimarea resortului, pe directie
verticala si apoi eliberand corpul, acesta va incepe sa oscileze
in jurul pozitiei de echilibru. Pozitia corpului in orice moment este
complet determinata prin abscisa x masurata de la pozitia
de echilibru x = 0. Prin conventie se considera ca axa lui x are
originea in pozitia de echilibru si sensul pozitiv indreptat in
sensul alungirii resortului.
In timpul miscarii
corpului de masa m in jurul
pozitiei de echilibru, in elementul elastic apare o forta Fe
dependenta de marimea si sensul deplasarii corpolui care
oscileaza. Totdeauna forta elastica Fe are sens
contrar deplasariicorpului, fiind indreptata spre pozitia de
echilibru.
Se spune ca oscilatorul este
liniar, daca forta elastica depinde liniar de deplasarea
corpului care oscileaza, fata de pozitia de echilibru. Oscilatia
corpului este liniara.
Daca oscilatiile corpului
fata de pozitia de echilibru sunt mici, ecuatia
miscarii corpului poate fi exprimata cu ajutorul functiilor
armonice sinus sau cosinus:
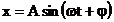 (1.1)
(1.1)
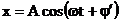 (1.2)
(1.2)
Daca ecuatia de
miscare a corpului care oscileaza poate fi scrisa cu ajutorul
functiilor armonice sinus sau cosinus atunci se spune ca oscilatorul
este armonic.
Oscilatorul armonic liniar
este acel oscilator a carei ecuatie de miscare este o
functie armonica de timp si pentru care forta elastica
ce apare in elementul elastic depinde liniar de deplasarea corpului care
oscileaza, fata de pozitia de echilibru.
Modelul oscilatorului armonic este o
idealizare a miscarii oscilatorii a sistemelor mecanice;
miscarile oscilatorii din natura si tehnica putand fi
exprimate doar in anumite limite cu ajutorul acestui model. Studierea
miscarilor mai complicate se poate aborda cu ajutorul unor modele mai
complexe care mai tin con si de actiunea altor forte asupra
sistemului mecanic (cum ar fi fortele perturbatoare sau fortele de
amortizare).
In ecuatia de miscare a oscilatorului armonic liniar intervin
urmatoarele marimi:
x elongatia,
sau deplasarea sistemului fata de pozitia de echilibru la un
moment dat;
A amplitudinea,
sau elongatia maxima;
w pulsatia, sau numarul
de oscilatii complete efectuate in timp de 2p secunde. Unitatea de masura in Sistemul International
este [w]SI =rad s-1;
T perioada
oscilatiei, sau timpul scurs intre doua treceri ale sistemului
oscilant prin acelasi punct, pe aceeasi directie si in
acelasi sens;
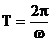 [T]SI
= s (1.3)
[T]SI
= s (1.3)
n frecventa oscilatiei,
sau numarul de oscilatii complete efectuate de sistem in unitatea de
timp;
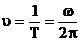 [n] SI = rad (1.4)
[n] SI = rad (1.4)
wt + j faza oscilatiei
(argumentul functiei sinus sau cosinus), exprimata in Sistemul
International in radiani;
j faza initiala, sau
diferenta de faza intre doua oscilatii a caror
ecuatii de miscare sunt:
x1 = Asin wt si x2 = Asin (wt + j (1.5)
j]SI = rad
Pentru oscilatorul armonic liniar a carui ecuatie de
miscare poate fi exprimata matematic sub forma relatiilor (1.1)
si (1.2), graficul variatiei elongatiei in timp este prezentat
in figura 2.
|
|
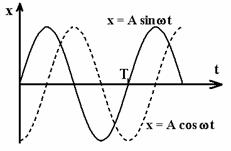 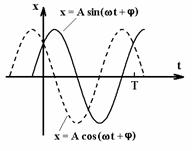
a)
b)
Fig.
2
|
|
Daca ecuatia de
miscare a corpului care oscileaza este descrisa de ecuatia
(1.1)
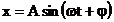
atunci viteza
corpului, exprimata ca derivata intaia a elongatiei in raport cu
timpul, este:
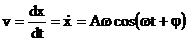 (1.6)
(1.6)
si
acceleratia corpului, exprimata ca derivata intaia a vitezei in
raport cu timpul, sau derivata a doua a elongatiei in raport cu timpul,
este:
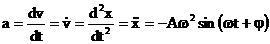 (1.7)
(1.7)
Asupra corpului de masa m, care
oscileaza va actiona o forta elastica:
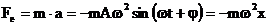 (1.8)
(1.8)
orientata
totdeauna in sens opus elongatiei. Aceasta forta este deci
o forta de tip central, numita forta elastica
si tinde sa aduca de fiecare data corpul care
oscileaza in pozitia de echilibru.
Pentru oscilatorul liniar,
forta elastica depinde liniar de elongatie si poate fi
scrisa sub forma:
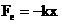 (1.9)
(1.9)
in care k se
numeste constanta elastica. 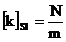
Comparand relatiile (1.8)
si (1.9) se obtine relatia dintre constanta elastica a
elementului elastic si pulsatia miscarii oscilatorii:
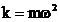 sau
sau 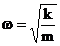 (1.10)
(1.10)
2
Constantele elastice ale unor elemente elastice cu un grad de libertate
Pentru a cunoaste ecuatia
de miscare a unui corp, care oscileaza armonic liniar, conform
relatiei (1.1), este necesar sa se cunoasca amplitudinea A, faza
initiala j si pulsatia w
Amplitudinea si faza
initiala se determina daca se cunosc conditiile
initiale ( elongatia x si viteza v la momentul initial t =
0) asa cum se va exemplifica in paragrafele urmatoare.
Pulsatia corpului de masa m, suspendat de un element elastic
conform figurii 1, se poate determina, daca se cunoaste constanta
elastica a elementului elastic, pe baza relatiei (1.10).
In general, pentru determinarea constantei elastice a unui element
elastic de lungime ℓ, se fixeaza unul din capetele elementului
elastic de un reper fix, ca in figura 3 si se actioneaza asupra
celuilalt capat cu o forta F, cunoscuta. Se
masoara alungirea Dℓ a
elementului elastic in urma actiunii fortei F. Daca alungirile
sunt mici, se poate considera ca forta elastica este
proportionala cu alungirea si prin aplicarea relatiei (1.9),
de proportionalitate, se poate scrie:
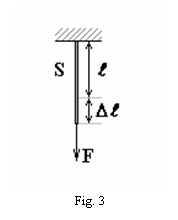
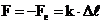 (2.1)
(2.1)
din care se poate calcula valoarea constantei elastice k.
In cazul unei bare
elastice, confectionate dintr-un material elastic, supuse unei forte
de intindere, se poate calcula constanta elastica k, din valoarea
modulului de elasticitate longitudinal E. Se
stie din legea lui Hook ca alungirea relativa 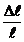 este
proportionala cu efortul unitar
este
proportionala cu efortul unitar 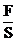 exercitat de
forta de intindere F asupra sectiunii transversale S a barei
elastice:
exercitat de
forta de intindere F asupra sectiunii transversale S a barei
elastice:
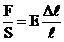 (2.2)
(2.2)
Comparand aceasta relatie cu relatia (2.1), se poate
exprima constanta elastica a elementului elastic, sub forma de
bara, in functie de lungimea acesteia, de aria sectiunii
transversale S si de natura materialului din care este
confectionata bara (exprimata pin modulul de elasticitate
longitudinal E, obtinut din tabele):
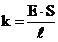 (2.3)
(2.3)
Exista si alte
relatii de calcul a constantelor elastice ale diverselor elemente elastice,
specifice fiecaruia.
In cazul in care un
anumit corp de masa m este fixat de repere fixe prin mai multe elemente
elastice este util sa se determine constanta elastica
echivalenta a tuturor elementelor elastice. Elementele elastice pot fi:
legate in paralel;
legate in serie;
legate mixt (unele in serie
si altele in paralel).
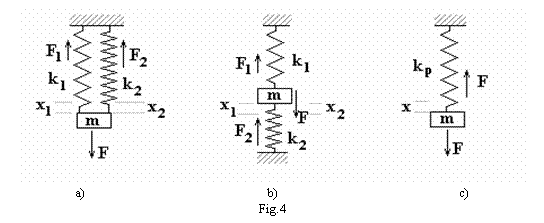
a)
Cazul in care elementele elastice
de constante elastice k1 respectiv k2, sunt
legate in paralel este prezentat schematic in figura 4 a) si b). Corpul de
masa m este suspendat prin intermediul acestor elemente elastice de repere
fixe. Se pune problema inlocuirii celor doua elemente elastice cu unul
singur, de constanta elastica echivalenta kp, ca in
figura 4 c) astfel incat miscarea corpului de masa m sa fie
identica.
Daca se scoate
sistemul din pozitia de echilibru, actionand cu o forta F,
in elementele elastice apar fortele F1 si F2 de
sens contrar fortei F astfel incat F = F1 + F2, in
care:
F1
= - k1x1 si
F2 = - k2x2 (2.4)
Daca se inlocuiesc
cele doua elemente elastice cu unul singur, pentru a obtine
aceeasi deplasare a corpului sub actiunea fortei F se poate
scrie ca x = x1 = x2 si deci:
F
= - k1x1 - k2x2 = - (k1
+ k2)x = - kpx (2.5)
Se obtine astfel constanta elastica echivalenta ca
fiind:
kp
= k1 + k2 (2.6)
In cazul in care sistemul
elastic este alcatuit din mai multe resorturi montate in paralel, prin
acelasi rationament, se obtine:
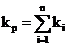 (2.7)
(2.7)
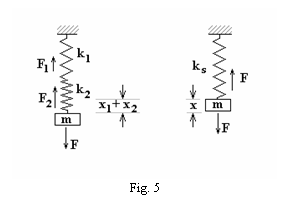
b)
Pentru un sistem elastic
alcatuit din mai multe resorturi, legate in serie, ca in figura 5, se
pune, la fel, problema inlocuirii celor doua elemente elastice, cu unul
singur, avand constanta elastica echivalenta ks astfel
incat miscarea corpului de masa m sa fie identica.
 Daca se
actioneaza cu forta F pentru a scoate sistemul din pozitia
de echilibru cu alungirea x, atunci in cele doua elemente elastice care se
alungesc cu x1 respectiv cu x2 vor apare fortele
elastice F1 si respectiv F2, care sunt egale cu
forta F:
Daca se
actioneaza cu forta F pentru a scoate sistemul din pozitia
de echilibru cu alungirea x, atunci in cele doua elemente elastice care se
alungesc cu x1 respectiv cu x2 vor apare fortele
elastice F1 si respectiv F2, care sunt egale cu
forta F:
F = F1 =
F2 (2.8)
Suma alungirilor celor
doua elemente elastice trebuie sa fie egala cu alungirea
totala x, sau cu alungirea elementului elastic echivalent:
x
= x1 + x2 (2.9)
in care: 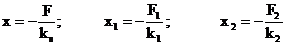 (2.10)
(2.10)
Prin inlocuirea alungirilor in relatia (2.9), se obtine:
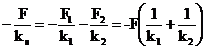 (2.11)
(2.11)
sau: 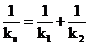 (2.12)
(2.12)
In cazul in care
exista mai multe resorturi legate in serie se poate generaliza rezultatul
anterior si printr-un rationament asemanator se obtine:
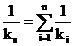 (2.13)
(2.13)
3
Cinematica miscarii oscilatorii
Compunerea
oscilatiilor armonice liniare paralele
In cazul in care un sistem este obligat sa se miste sub
actiunea simultana a doua oscilatii diferite, insa pe
aceeasi directie:
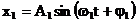 (1)
(1)
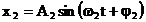 (2)
(2)
el va executa o miscare compusa.
Prezinta interes
urmatoarele trei situatii:
Compunerea oscilatiilor armonice
liniare paralele de aceeasi pulsatie
In
acest caz cele doua oscilatii
care se compun au ecuatiile:
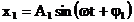 (3)
(3)
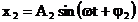 (4)
(4)
Oscilatia rezultanta a sistemului va avea ecuatia:
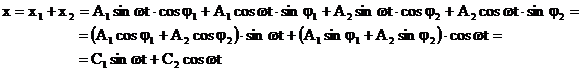 (5)
(5)
in
care: 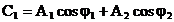 (6)
(6)
si: 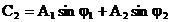 (7)
(7)
sunt
doua constante care depind de amplitudinile si fazele initiale
ale celor doua oscilatii care se compun.
Relatia (5) mai poate fi
scrisa si sub forma:
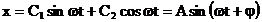 (8)
(8)
deoarece
o combinatie liniara de doua functii armonice, de
aceeasi pulsatie, este tot o functie armonica, de
pulsatie identica cu a celor doua oscilatii. Amplitudinea A
si faza initiala j pot fi
exprimate in functie de amplitudinile si fazele initiale ale oscilatiilor
care se compun.
Relatia (8) poate fi dezvoltata in continuare
si va avea forma:
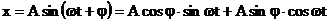 (9)
(9)
Identificand cei doi termeni cu cei din relatia(5)
se obtine sistemul de ecuatii:
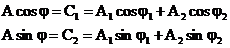 (10)
(10)
Rezolvand sistemul de ecuatii se pot obtine
expresiile amplitudinii:
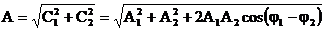 (11)
(11)
si fazei initiale:
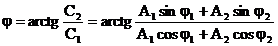 (12)
(12)
pentru oscilatia rezultanta.
Din cele doua relatii (11) si (12) se
observa ca daca j j ,
oscilatiile sunt in faza si:
A = A1 + A2 iar j j j (13)
Daca j j p, oscilatiile sunt in opozitie
de faza si:
A
= A1 - A2 iar j j j p (14)
Cele doua cazuri de
oscilatii discutate anterior sunt prezentate grafic in figura 6
|
|
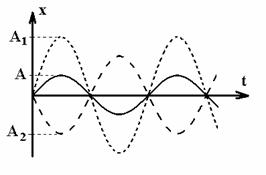 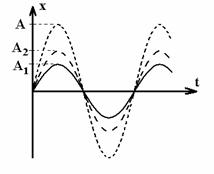
a)
b)
Fig.
6
|
|
1.2 Compunerea oscilatiilor armonice liniare paralele
de pulsatii diferite
Cele doua oscilatii care
se compun sunt descrise de relatiile (1) si (2). In urma compunerii
celor doua oscilatii se obtine o combinatie liniara de
doua functii armonice de pulsatii diferite. Miscarea
oscilatorie rezultanta este descrisa, in acest caz, de o functie
nearmonica in timp, de forma:
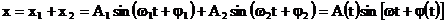 (15)
(15)
Atat amplitudinea cat si faza initiala a
miscarii rezultante nu sunt constante ci sunt functii variabile
in timp. Daca numai amplitudinea miscarii nearmonice este
functie variabila in timp se spune ca miscarea
nearmonica este modulata in amplitudine (liniar, exponential,
armonic, etc.; in functie de expresia liniara exponentiala
sau armonica de variatie a amplitudinii in timp). De exemplu,
oscilatiile unui pendul liber sunt nearmonice, modulate exponential
in amplitudine.
Miscarea oscilatorie
nearmonica descrisa de relatia (15) are in general o expresie
complicata in functie de valorile amplitudinilor A1
si A2, a fazelor initiale j si j precum si a pulsatiilor w si w . Un caz particular este acela in care
pulsatiile sunt intr-un raport egal cu un numar intreg si mic.
Compunerea se poate realiza in acest caz pe cale grafica asa cum este
prezentat in exemplul din figura 7.
|
|
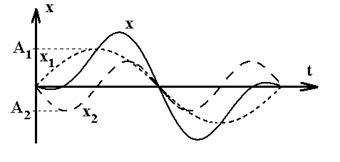
Fig.
7
|
|
1.3 Compunerea oscilatiilor armonice liniare paralele
de pulsatii putin diferite. Batai
Prezinta
importanta practica si teoretica situatia in care
pulsatiile celor doua oscilatii care se compun, descrise de
relatiile (1) si (2), sunt putin diferite. Intre cele doua
pulsatii se pot scrie relatiile:
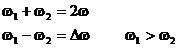 (16)
(16)
in care Dw este diferenta dinte pulsatiile
celor doua oscilatii care se compun, iar w este valoarea medie a celor doua pulsatii.
Cele doua
pulsatii pot fi scrise, printr-un artificiu matematic, sub forma:
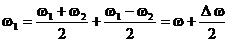 (17)
(17)
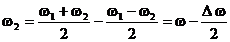 (18)
(18)
Tinand cont de
acestea, expresiile (1) si (2) pot fi scrise:
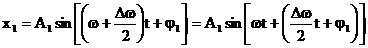 (19)
(19)
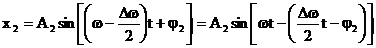 (20)
(20)
Daca se
noteaza: 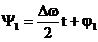 (21)
(21)
si 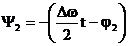 (22)
(22)
relatiile (19) si (20) se pot scrie:
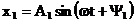 (23)
(23)
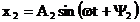 (24)
(24)
Se observa acum,
ca aceste expresii sunt, formal, asemanatoare cu relatiile
(3) si (4). Repetand acelasi rationament ca cel prezentat la la
compunerea oscilatiilor armonice paralele de aceeasi pulsatie,
se obsine ecuatia miscarii oscilatorii rezultante:
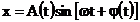 (25)
(25)
in care:
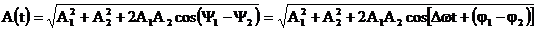 (26)
(26)
si: 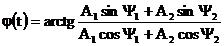 (27)
(27)
Deoarece Y si Y sunt functii variabile in timp, atat
amplitudinea cat si faza initiala a miscarii
oscilatorii rezultante sunt functii variabile in timp, astfel incat
oscilatia rezultanta nu este o miscare oscilatorie
armonica. Graficul acestei miscari este reprezentat in figura 8.
|
|
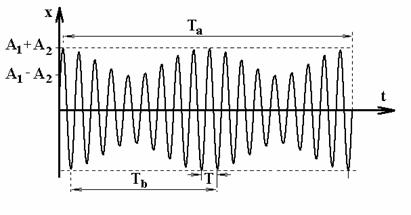
Fig.
8
|
|
Oscilatia
rezultanta este nearmonica modulata armonic in timp de
amplitudine ce variaza intre Amax. = A1 + A2
si Amin. = A1 - A2 (daca A1
> A2).
Perioada de variatie
a amplitudinii este:
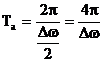 (28)
(28)
Apare astfel, un fenomen
de crestere si scadere periodica a amplitudinii
oscilatiei rezultante. Acest fenomen este cunoscut in tehnica sub
numele de "fenomenul de batai". Perioada batailor este
jumatate din perioada de modificare a amplitudinii, adica:
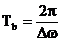 (29)
(29)
Frecventa
batailor este egala cu diferenta frecventelor celor
doua oscilatii:
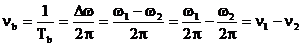 (30)
(30)
Daca diferenta
dintre frecventele celor doua oscilatii este prea mare,
frecventa batailor este de asemenea mare si fenomenul nu
este perceptibil. De asemenea, atunci cand diferenta frecventelor
celor doua oscilatii care se compun este prea mica,
frecventa batailor este atat de mica incat fenomenul este
din nou greu perceptibil. In acest caz, pe parcursul perioadei unei
batai, se poate considera miscarea oscilatorie ca fiind
armonica.
Daca cele doua
oscilatii care se compun au amplitudini egale, se obtine cazul
particular reprezentat grafic in figura 9.
In acest caz:
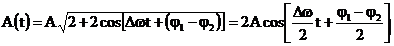 (31)
(31)
|
|
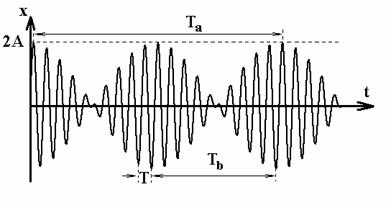
Fig. 9
|
|
cu Amax. = 2A si Amin. = 0.
De asemenea:
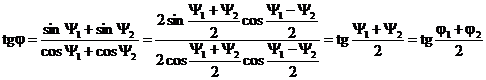 (32)
(32)
deci faza initiala j nu mai este
o functie de timp, oscilatia rezultanta fiind nearmonica,
modulata doar in amplitudine, avand ecuatia: 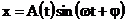 (33)
(33)
Principalele
aplicatii ale fenomenului de batai sunt in domeniul acusticii,
la determinarea frecventelor unor oscilatii sonore necunoscute. De
asemenea, fenomenul este utilizat in electrotehnica, cand se cupleaza
in paralel alternatorii, precum si in radiotehnica.
2
Compunerea oscilatiilor armonice liniare perpendiculare
Daca un sistem este obligat
sa oscileze simultan dupa doua directii perpendiculare,
ecuatia de miscare a acestuia este mai complicata.
In continuare sunt tratate cele
doua cazuri de compuneri de oscilatii armonice liniare, perpendiculare:
de aceeasi pulsatie;
de pulsatii diferite.
2.1 Compunerea oscilatiilor armonice liniare
perpendiculare de aceeasi pulsatie
Cele doua oscilatii armonice
liniare, perpendiculare, de aceeasi pulsatie, care se compun au
ecuatiile:
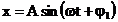 (34)
(34)
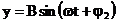 (35)
(35)
Un punc material supus
actiunii simultane a celor doua oscilatii va descrie in planul
xOy si in timpul T (perioada comuna celor doua oscilatii
perpendiculare), o traiectorie inchisa, a carei ecuatie se va
obtine eliminand timpul intre cele doua ecuatii de miscare.
Pentru aceasta se dezvolta cele doua ecuatii de miscare
descrise anterior, obtinandu-se:
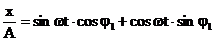 (36)
(36)
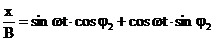 (37)
(37)
In continuare se
inmulteste relatia (36) cu 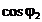 si relatia (37)
cu
si relatia (37)
cu  . Facand diferenta dintre relatiile
inmultite se obtine:
. Facand diferenta dintre relatiile
inmultite se obtine:
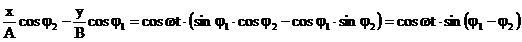 (38)
(38)
De asemenea
inmultind relatia (36) cu 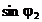 si relatia (37)
cu
si relatia (37)
cu 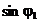 , apoi facand diferenta intre relatiile
inmultite se obtine:
, apoi facand diferenta intre relatiile
inmultite se obtine:
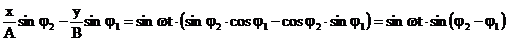 (39)
(39)
Pentru a elimina timpul
intre noile relatii (38) si (39) se ridica la patrat
fiecare expresie, se aduna si in acelasi timp se grupeaza
termenii, obtinandu-se in final expresia:
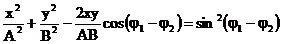 (40)
(40)
Daca notam
diferenta dintre fazele initiale ale celor doua oscilatii
armonice perpendiculare j j j se obtine expresia ecuatiei de miscare a sistemului
supus actiunii simultane a doua oscilatii perpendiculare
descrise de ecuatiile (34) si (35):
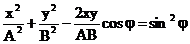 (41)
(41)
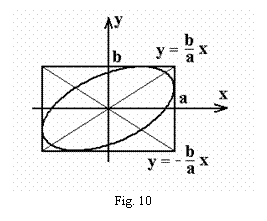 Aceasta reprezinta
ecuatia unei elipse. Forma elipsei reprezentata schematic in figura 10
depinde de raportul amplitudinilor celor doua oscilatii
perpendiculare care se compun si de diferenta de faza j, dintre cele doua oscilatii.
Aceasta reprezinta
ecuatia unei elipse. Forma elipsei reprezentata schematic in figura 10
depinde de raportul amplitudinilor celor doua oscilatii
perpendiculare care se compun si de diferenta de faza j, dintre cele doua oscilatii.
Amplitudinile
A si B fiind cunoscute si pozitive, orientarea si forma
elipsei-traiectorie va depinde exclusiv de diferenta de faza j dintre cele doua oscilatii.
Se
pot considera urmatoarele trei cazuri caracteristice:
Pentru cazul in care j = 0, ecuatia elipsei degenereaza in ecuatia unei drepte
prezentata in figura 10, de ecuatie:
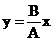 (42)
(42)
Pentru cazul in care 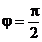 ecuatia (41)
devine:
ecuatia (41)
devine:
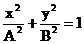 (43)
(43)
Aceasta este ecuatia
unei elipse cu semiaxele orientate dupa axele Ox si Oy. Si mai
particular este cazul in care A = B = R. In acest caz elipsa degenereaza
intr-un cerc de raza R de ecuatie 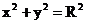 .
.
Pentru cazul in care j p, elipsa degenereaza din nou intr-o
dreapta de ecuatie:
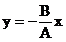 (44)
(44)
Traiectorile descrise de
oscilatia rezultanta si sensurile de parcurgere ale acestora,
pentru diferite valori ale diferentei de faza j sunt prezentate in figura 11.
Cand traiectoria este
parcursa in sensul miscarii acelor unui ceasornic se spune
ca oscilatia rezultanta este polarizata eliptic spre dreapta,
iar cand traiectoria este parcursa in sens invers miscarii
acelor unui ceasornic se spune ca oscilatia rezultanta este
eliptic polarizata spre stanga. Cand traiectoria are forma uneia dintre
cele doua drepte se spune ca
oscilatia rezultanta este liniar polarizata.
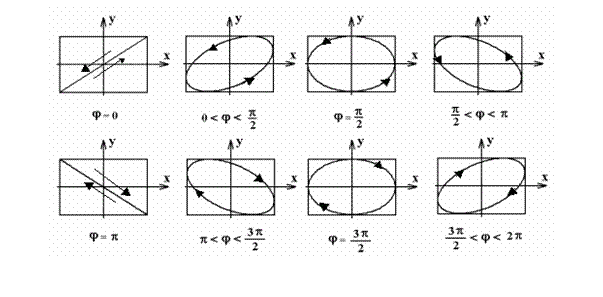 fig. 11
fig. 11
2.1 Compunerea oscilatiilor armonice liniare
perpendiculare de pulsatii diferite
Daca cele doua
oscilatii perpendiculare au pulsatii diferite, descrise de
ecuatiile: 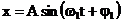 (45)
(45)
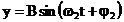 (46)
(46)
atunci traiectoria descrisa de sistemul supus actiunii
simultane a celor doua oscilatii in planul xOy poate sa fie o
curba inchisa, sau o curba deschisa.
Pentru ca traiectoria
sa fie o curba inchisa trebuie ca dupa un interval de timp,
sistemul sa treaca prin acelasi punct, in aceeasi
directie si sens. Intervalul minim de timp T, dupa care
miscarea sistemului se repeta identic, trebuie sa fie in
acelati timp un multiplu atat al perioadei primei oscilatii
descrisa de ecuatia (45), cat si al perioadei celei de-a doua
oscilatii descrisa de ecuatia (46). Deci:
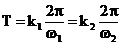 (47)
(47)
De aici rezulta ca daca raportul celor doua
pulsatii este un numar rational:
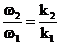 (48)
(48)
traiectoria descrisa de sistem este o curba inchisa.
Daca raportul
pulsatiilor celor doua oscilatii care se compun este un
numar irational, traiectoria miscarii oscilatorii
rezultante este o curba deschisa.
Forma traiectoriei descrise de un sistem mecanic supus actiunii
simultane a doua oscilatii perpendiculare de pulsatii diferite
depinde de raportul amplitudinilor celor doua oscilatii 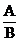 , de raportul pulsatiilor
, de raportul pulsatiilor 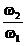 si de
diferenta de faza j dintre cele
doua oscilatii.
si de
diferenta de faza j dintre cele
doua oscilatii.
Figurile care descriu
traiectoriile sistemului mecanic sun cunoscute sub numele de "figurile
lui Lissajous" deoarece au fost prezentate pentru prima data de
fizicianul francez Jules Antoine Lissajous (1822-1880) in anul 1857.
In figura 12 sunt
prezentate cateva figuri ale lui Lissajous corespunzatoare unui defazaj
dintre cele doua oscilatii perpendiculare j
|
|
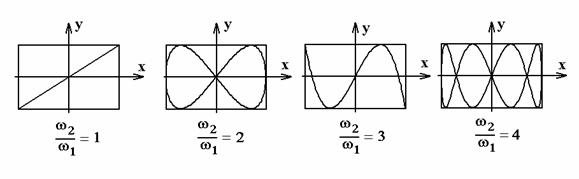 Fig.12 Fig.12
|
|
3
Compunerea oscilatiilor armonice liniare pe directii oarecare
In cazul in care asupra
unui sistem mecanic actioneaza simultan doua oscilatii care
formeaza un unghi oarecare intre ele, ca in figura 13, se poate alege
totdeauna un sistem de coordonate xOy astfel incat axa Ox sa
corespunda cu directia unei oscilatii.
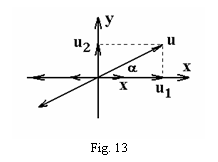 Ecuatia acestei
oscilatii va fi:
Ecuatia acestei
oscilatii va fi:
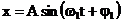 (49)
(49)
Cea de-a doua
oscilatie va forma cu directia primei oscilatii un unghi a iar ecuatia acestei oscilatii este:
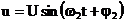 (50)
(50)
Aceasta
oscilatie va fi descompusa in doua componente
corespunzatoare proiectiilor pe cele doua axe, Ox si Oy,
obtinandu-se:
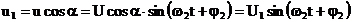 (51)
(51)
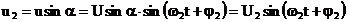 (52)
(52)
In continuare se pot
compune oscilatiile x si u1, descrise de ecuatiile (49)
si (51) ca doua oscilatii paralele, obtinandu-se
oscilatia rezultanta: v = x + u1. In continuare se compun
oscilatiile v si u2 ca doua oscilatii
perpendiculare, obtinandu-se in final oscilatia rezultanta
finala:
z = u2 +v (53)
In etapele intermediare
de compunere a oscilatiilor paralele sau perpendiculare se pot intalni
oricare din cazurile prezentate anterior, in paragraful 1 sau 2.







 Daca se
actioneaza cu forta F pentru a scoate sistemul din pozitia
de echilibru cu alungirea x, atunci in cele doua elemente elastice care se
alungesc cu x1 respectiv cu x2 vor apare fortele
elastice F1 si respectiv F2, care sunt egale cu
forta F:
Daca se
actioneaza cu forta F pentru a scoate sistemul din pozitia
de echilibru cu alungirea x, atunci in cele doua elemente elastice care se
alungesc cu x1 respectiv cu x2 vor apare fortele
elastice F1 si respectiv F2, care sunt egale cu
forta F: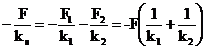 (2.11)
(2.11)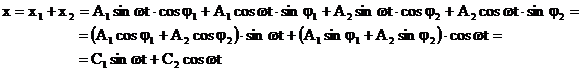 (5)
(5)



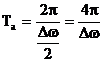 (28)
(28)
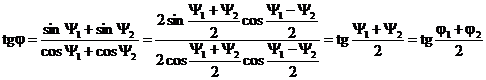 (32)
(32) Aceasta reprezinta
ecuatia unei elipse. Forma elipsei reprezentata schematic in figura 10
depinde de raportul amplitudinilor celor doua oscilatii
perpendiculare care se compun si de diferenta de faza
Aceasta reprezinta
ecuatia unei elipse. Forma elipsei reprezentata schematic in figura 10
depinde de raportul amplitudinilor celor doua oscilatii
perpendiculare care se compun si de diferenta de faza 
 Fig.12
Fig.12 Ecuatia acestei
oscilatii va fi:
Ecuatia acestei
oscilatii va fi: