econometrie
Import, produs intern brut, indicele preturilor
bunurilor de consum
Analiza econometrica
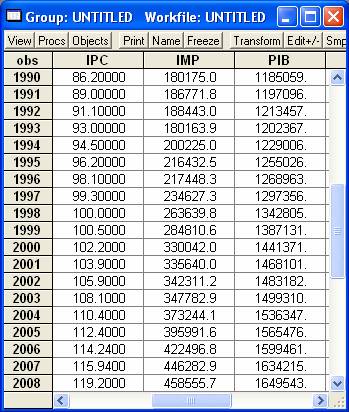
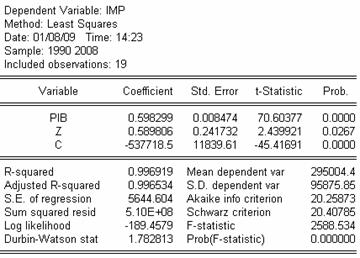
Am preluat datele pentru produsul intern brut (PIB)
si valoarea anuala totala a importurilor (IMP) pentru
Franta de pe site-ul EuroStat. Pentru acesti doi indicatori unitatea
de masura folosita este milioane
de euro, iar pentru a asigura comparabilitatea datelor am preluat acele
date care au ca baza de comparatie anul 2000. Valorile anuale ale
indicilor preturilor bunurilor de consum (IPC) au fost preluate de pe
site-ul www.insee.fr. Datele au valori
anuale, acoperind perioada 1990-2008. Acestea sunt redate in continuare.
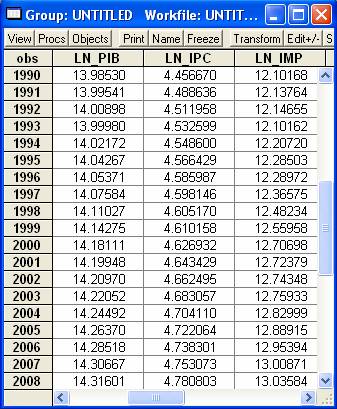
Cu ajutorul comenzii Proc→Generate Series am generat si seriile logaritmice
ale acestor serii de date (in dreapta: LN_PIB, LN_IPC, LN_IMP).
Mai intai voi caracteriza relatia dintre valoarea importurilor si
produsul intern brut, definita prin urmatorul model de regresie:
IMPi = a1
+ b1 * PIBi + εi i=1..19 (1) marimea esantionului este de 19
observatii in acest caz
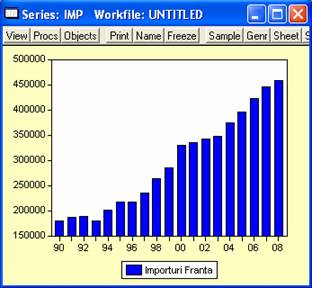
Am reprezentat grafic evolutia importului in perioada analizata.
Se observa din fig.3 ca predomina o tendinta generala
de crestere a valorilor importurilor de la un an la altul, singura
exceptie inregistrandu-se in anul 1993, cu o valoare a importurilor mai
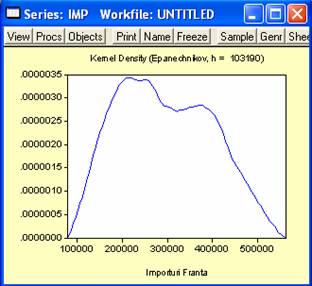
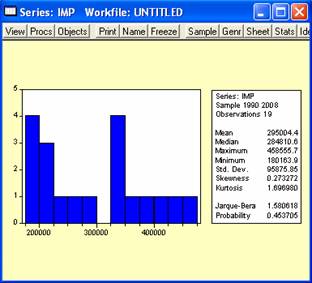
mica decat in anul precedent. Am caracterizat distributia variabilei
IMP prin utilizarea comenzilor View→Descriptive
Statistics→Histogram and Stats
In acest fel am obtinut valorile mediei, medianei, dispersiei,
valorii minime si maxime, si alte caracteristici ale
distributiei.
Urrmaresc sa descriu dependenta
dintre variabila PIB si IMP. Pentru aceasta am realizat graficul "norului
de puncte", grafic in care sunt reprezentate cele 2 caracteristici pe axe
diferite.
Prin utilizarea comenzii Graph→Scatter→Scatter
with regression s-a obtinut graficul urmator, grafic ce
contine si dreapta de regresie corespunzatoare.
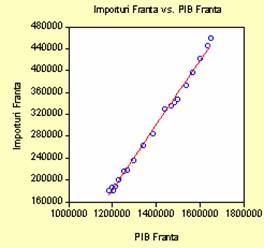
Se observa o dependenta directa, pozitiva intre
valoarea produsului intern brut si valoarea importurilor. Cu cat PIB-ul
creste cu atat Franta importa un volum mai mare de bunuri
si servicii.
Dreapta reprezentata este de fapt dreapta de regresie
corespuntatoare modelului (1), ai carei parametrii trebuie
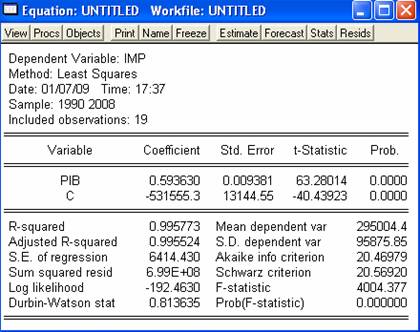
estimati. Valorile estimatorilor, rezultate in urma aplicarii metodei
celor mai mici 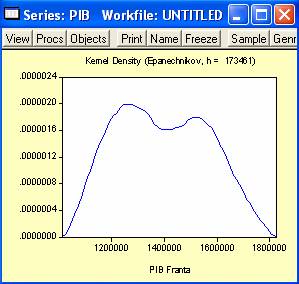 patrate, sunt date in urmatorul
tabel. Ceea ce a rezultat este ca dependenta certa dintre
valorea variabilei PIB si IMP este asigurata de valoarea
substantial diferita de zero a coeficientului b1=0.593. Valoarea
coeficientului b1 se interpreteaza astfel: la cresterea cu
o unitate a PIB-ului, importurile cresc in medie cu 0.593 unitati.
Estimatorul termenului liber are valoarea -531555.3, dar nu are interpretare
economica. In acest tabel ne sunt furnizate si alte informatii
referitoare la valorile statisticilor t si F, intre care se verifica
relatia t2=F sau valoarea raportului de determinare R2=0.995773.
Deoarece aceasta valoare este extrem de apropiata de 1 putem conclude
ca dependenta dintre cele 2 variabile este una directa (deoarece
e pozitiva) si puternica. Mai putem citi din tabel valoarea
ajustata a coeficientului de corelatie, suma patratelor
erorilor, valoarea statistici Durbin-Watson de care ma voi lega intr-o
etapa urmatoarea a proiectului.
patrate, sunt date in urmatorul
tabel. Ceea ce a rezultat este ca dependenta certa dintre
valorea variabilei PIB si IMP este asigurata de valoarea
substantial diferita de zero a coeficientului b1=0.593. Valoarea
coeficientului b1 se interpreteaza astfel: la cresterea cu
o unitate a PIB-ului, importurile cresc in medie cu 0.593 unitati.
Estimatorul termenului liber are valoarea -531555.3, dar nu are interpretare
economica. In acest tabel ne sunt furnizate si alte informatii
referitoare la valorile statisticilor t si F, intre care se verifica
relatia t2=F sau valoarea raportului de determinare R2=0.995773.
Deoarece aceasta valoare este extrem de apropiata de 1 putem conclude
ca dependenta dintre cele 2 variabile este una directa (deoarece
e pozitiva) si puternica. Mai putem citi din tabel valoarea
ajustata a coeficientului de corelatie, suma patratelor
erorilor, valoarea statistici Durbin-Watson de care ma voi lega intr-o
etapa urmatoarea a proiectului.
Doresc sa testez
daca valoarea coeficientului pantei difera semnificativ de zero.
Pentru aceasta folosesc testul t-Student.
Am definit ipotezele testului
statistic:
H0: b1=0;
H1: b1≠0;
Se
defineste statistica testului:
t=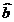 1/
1/ 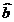 1 t19-2
1 t19-2
Conform datelor din tabelul de mai sus, tcalc=63.28, iar pentru un prag de semnificatie de 5%
si 17 grade de libertate tα/2,17=2.567.
Cum tcalc>tα/2,17
se accepta ipoteza alternativa conform careia panta dreptei de
regresie difera semnificativ de zero.
In
tabelul care caraterizeaza regresia analizata, in coloana Prob avem pragul de semnificatie. Daca
valoarea acestuia e mai mica decat 0.05 atunci se respinge ipoteza
nula.
Voi testa daca valoarea coeficientului pantei
dreptei de regresie difera semnificativ de 1. Pentru aceasta definesc
ipotezele testului statistic:
H0: b1=1
H1: b1≠1
Statistica testului
este t = 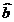 1-1/
1-1/ 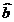 1→ t19-2
1→ t19-2
t = 0.59363-1/0.009381 = -43.31 =st1
Am aflat aceasta valoare prin utilizarea comenzii Scalar st1=(@coefs(1)-1)/@stderrs(1)
Dupa ce,
in prealabil, am definit modelul de regresie in EViews prin comanda
Equation EQ1.IS IMP c PIB
Pentru luarea unei decizii determin o cuantila a repartitiei
t-Student pentru pragul de semnificatie de 0.05 si 17 grade de
libertate. Am folosit comanda
Scalar vqst1=@qtdist(0.05,17)
Valoarea vqst1 = -1.739
Deoarece |tcalc|≥t0.05 se accepta ipoteza nula si anume se
poate spune ca valorea estimatorului pentru coeficientul pantei nu
difera semnificativ de 1.
Pentru a gasi cu ce
probabilitate valoarea importurilor se gaseste intre 2 valori (300000
si 400000) se tine cont de urmatoarele consideratii.
Φ(x) 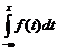 , unde
, unde
f(t)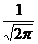 exp(-
exp(-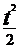 )
)
Variabila IMP ~ N(295004, 95876)
Prob_IMP = P((300000-295004)/95876<(IMP-295004)/95876<(400000-295004)/95876)=Φ(0.513)-Φ(-1.043)
scalar Prob_IMP=@cnorm(0.513)-@cnorm(-1.043)
Probabilitatea care se obtine este de 54.75%.
In variabila
Prob_IMP se salveaza valoarea probabilitatii.
Pentru a determina daca
modelul de regresie este semnificativ preiau din tabelul distributiei F valoarea
predeterminata pentru un prag de semnificatie de 0.05.
k-1=2-1=1
n-k=19-2=17
F0.05 =4.45
Cum Fcalc=4004.377>
F0.05 atunci modelul de regresie este
semnificativ.
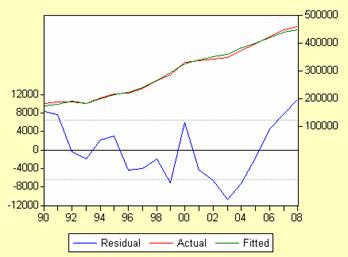
In continuare urmaresc sa confirm sau
anulez proprietatea de autocorelare a
erorilor pentru modelul de regresie analizat.
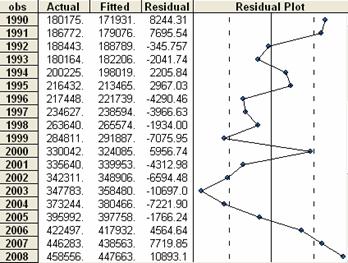
In prima figura se prezinta pe doua
scale graficul valorilor reale si cel al celor estimate ale
caracteristicii IMP, scala din partea stanga, precum si cea a
rezidurilor, scala din dreapta. Intr-o alta forma de prezentare avem
intr-un tabel valorile reale ale importurilor, cele ajustate, precum si
ale rezidurilor. Este prezentat, de asemenea, un grafic al rezidurilor in
paralel.
 Pentru
a pune in evidenta corelatia
de ordinul intai poate fi reprezentata grafic in Eviews seria de date (
Pentru
a pune in evidenta corelatia
de ordinul intai poate fi reprezentata grafic in Eviews seria de date (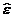 i-1,
i-1, 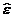 i)i=2, 19
i)i=2, 19
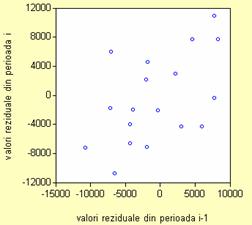
Pentru aceast lucru se foloseste urmatoarea instructiune in
Eviews:
scat resid(-1) resid
S-a
obtinut urmatorul grafic:
 O
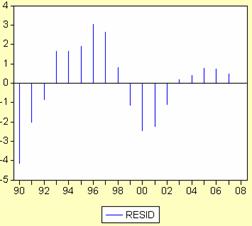
alta reprezentare a rezidurilor se vede in
graficul urmator. Se obsrva o anumita
sezonalitate a datelor, erorile osciland intre perioade cu valoare
negativa sau pozitiva. Inainte de a
aplica testul de verificare a autocorelarii, se observa din grafic
ca punctele sunt dispuse in jurul unei drepte. Acest
fapt implica prezenta autocorelarii. Pentru a verifica
daca erorile sunt corelate de ordinal I sau nu se aplica testul
Durbin-Watson. Valoarea statisticii acestui test se gaseste in
tabelul caracteristicilor regresiei si are
valoarea 0.8136. Pentru a lua o decizie preluam din tabelul
distributiei Durbin-Watson valorile DU si DL
corespunzatoare unui prag de semnificatie de 0.05, pentru 2 parametrii
si 19 observatii.
O
alta reprezentare a rezidurilor se vede in
graficul urmator. Se obsrva o anumita
sezonalitate a datelor, erorile osciland intre perioade cu valoare
negativa sau pozitiva. Inainte de a
aplica testul de verificare a autocorelarii, se observa din grafic
ca punctele sunt dispuse in jurul unei drepte. Acest
fapt implica prezenta autocorelarii. Pentru a verifica
daca erorile sunt corelate de ordinal I sau nu se aplica testul
Durbin-Watson. Valoarea statisticii acestui test se gaseste in
tabelul caracteristicilor regresiei si are
valoarea 0.8136. Pentru a lua o decizie preluam din tabelul
distributiei Durbin-Watson valorile DU si DL
corespunzatoare unui prag de semnificatie de 0.05, pentru 2 parametrii
si 19 observatii.
DU=1.08
DL=1.53
Cum valoarea calculata Dcalc<DU
se respinge ipoteza nula a absentei
autocorelarii erorilor. Deci eroarea din anul t-1are o
influenta asupra erorii din anul t.
 Este
necesar sa estimez parametrii modelului de
regresie prin eliminarea autocorelarii erorilor. Pentru acest lucru
memorez valorile rezidurilor in variabila ERR1 cu ajutorul comenzii genr err1=resid
Este
necesar sa estimez parametrii modelului de
regresie prin eliminarea autocorelarii erorilor. Pentru acest lucru
memorez valorile rezidurilor in variabila ERR1 cu ajutorul comenzii genr err1=resid
Estimez parametrii modelului de
regresie:
IMPi= a1 + b1 * PIBi
+ c1 * Z, Z0=0, Zi=ERR1i-1, i=2..19
Acest model are caracteristicile alaturate.
 Acest model de regresie nu prezinta
fenomenul de autocorelare a erorilor. Deoarece estimatorul pentru variabila Z
are o valoare semnificativ diferita de zero, putem spune ca erorile sunt
puternic corelate in modelul precedent.
Acest model de regresie nu prezinta
fenomenul de autocorelare a erorilor. Deoarece estimatorul pentru variabila Z
are o valoare semnificativ diferita de zero, putem spune ca erorile sunt
puternic corelate in modelul precedent.
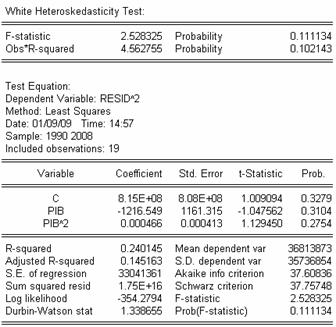
Heteroschedasticitate
Pentru a verifica daca modelul respecta proprietatea de
homoschedasticitate am folosit testul
White direct implementat in Eviews: View/Residual Tests/White
Heteroskedasticity (Cross Terms sau No Cross Terms sunt la fel pentru cazul
cu 2 parametrii). Statistica testului este W=T*R2→χ21
Wcalc=19*0.240145=4.56, iar valoarea tabelara a
distributiei χ2,
pentru un grad de libertate este 3.84. Pentru a lua decizia testului
comparam cele 2 valori. Cum Wcalc>3.84, spunem ca
fenomenul de heteroschedasticitate este prezent in model.
 Caracterizez relatia dintre valoarea
importurilor Frantei si indicele preturilor de consum prin
urmatorul model de regresie simpla:
Caracterizez relatia dintre valoarea
importurilor Frantei si indicele preturilor de consum prin
urmatorul model de regresie simpla:
IMPi = a2
+ b2 * IPCi + εi i=1..19 (2)
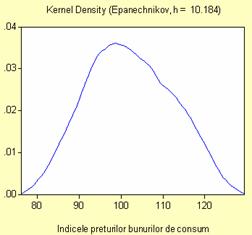
Am realizat un grafic al evolutiei indicelui preturilor bunurilor
de consum, precum si cel al distributiei acestuia. Se observa
ca distributia este una normala. Din graficul urmator se
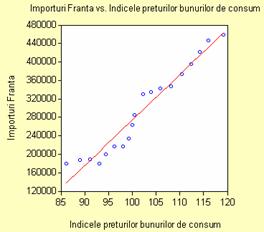
observa o dependenta directa intre valoarea indicilor
preturilor bunurilor de consum si valoarea importurilor.
 Din datele furnizate in tabelul rezultat
in urma estimarii parametrilor prin metoda celor mai mici patrate
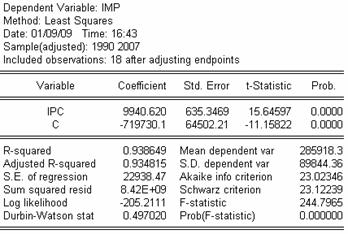
putem citi ca estimatorul pantei dreptei de regresie are valoarea b2=9940.620,
care se poate interpreta astfel: la cresterea indicelui preturilor cu
o unitate, valoarea importurilor creste in medie cu 9940.620
unitati. Dreapta de regresie este si ea reprezentata in
graficul alaturat. Valoarea estimatorului termenului liber este de
-719730.1, dar nu are interpretare economica. Deoarece valoarea raportului
de determinare este foarte apropiata de 1, dependenta dintre cele 2
variabile este directa si puternica.
Din datele furnizate in tabelul rezultat
in urma estimarii parametrilor prin metoda celor mai mici patrate
putem citi ca estimatorul pantei dreptei de regresie are valoarea b2=9940.620,
care se poate interpreta astfel: la cresterea indicelui preturilor cu
o unitate, valoarea importurilor creste in medie cu 9940.620
unitati. Dreapta de regresie este si ea reprezentata in
graficul alaturat. Valoarea estimatorului termenului liber este de
-719730.1, dar nu are interpretare economica. Deoarece valoarea raportului
de determinare este foarte apropiata de 1, dependenta dintre cele 2
variabile este directa si puternica.
Vreau sa pun in evidenta prezenta sau absenta
fenomenului de autocorelare a erorilor.
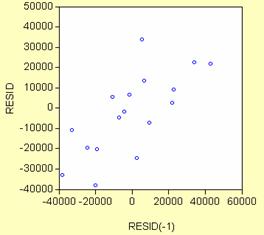 Deoarece din graficul urmator se
observa ca erorile sunt asezate de-a lungul unei drepte, putem
afirma ca erorile sunt corelate. Pentru a verifica daca
erorile sunt corelate de ordinal I sau nu se aplica testul Durbin-Watson.
Valoarea statisticii acestui test se gaseste in tabelul
caracteristicilor regresiei si are valoarea
0.497. Pentru a lua o decizie preluam din tabelul distributiei
Durbin-Watson valorile DU si DL corespunzatoare unui
prag de semnificatie de 0.05, pentru 2 parametrii si 19
observatii.
Deoarece din graficul urmator se
observa ca erorile sunt asezate de-a lungul unei drepte, putem
afirma ca erorile sunt corelate. Pentru a verifica daca
erorile sunt corelate de ordinal I sau nu se aplica testul Durbin-Watson.
Valoarea statisticii acestui test se gaseste in tabelul
caracteristicilor regresiei si are valoarea
0.497. Pentru a lua o decizie preluam din tabelul distributiei
Durbin-Watson valorile DU si DL corespunzatoare unui
prag de semnificatie de 0.05, pentru 2 parametrii si 19
observatii.
DU=1.08
DL=1.53
Cum valoarea calculata Dcalc<DU
se respinge ipoteza nula a absentei
autocorelarii erorilor. Deci eroarea din anul t-1are o
influenta asupra erorii din anul t.
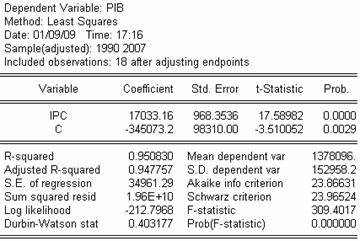
Analizez dependenta dintre valoarea produsului intern brut si
valoarea indicilor preturilor bunurilor de consum prin urmatorul model
de regresie:
PIBi = a3
+ b3 * IPCi + εi i=1..19 (3)
Din studierea diferitelor valori obtinute in
tabelul alaturat putem afirma ca ecuatia reprezinta un
model de regresie.
Din nou erorile sunt autocorelate. Acest lucru se
vede din valoarea statisticii Durbin-Watson si din graficele
urmatoare.
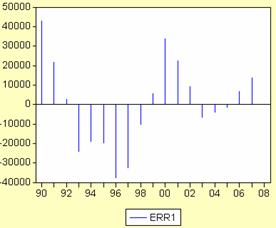
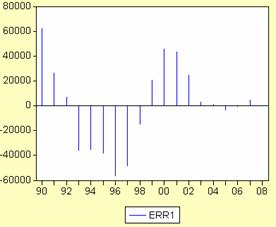
In urma aplicarii testului White pentru ultimele doua
ecuatii a rezultat prezenta fenomenului de heteroschedasticitate in
ambele cazuri.
Am aplicat si testul Arch
pentru modelul de regresie (1), pentru 8 orizonturi de timp (q)
et2=a0+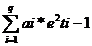 Valoarea statisticii este A=19*R2=18.95→χ21
Valoarea statisticii este A=19*R2=18.95→χ21
 Valoarea tabelata din
distributia χ2
este 3.84. Cum Acalc>Atab spunem ca
exista cel putin un estimator care difera semnificativ de zero,
ceea ce implica prezenta heteroschedasticitatii. Am ales
modelul cu 8 orizonturi de timp, deoarece in urma estimarii mai multor
variante, acestui model ii corespundea valoarea cea mai mica pentru Akaike
Info Criterion. Interpretarea care poate fi data modelului in urma
acestui test este ca datele de acum 8 ani influenteaza
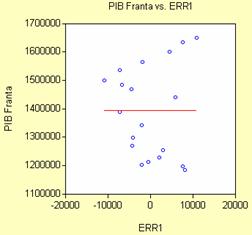
prezentul. Din graficul alaturat se observa si o dispunere in
forma de "palnie"a punctelor (dependenta dintre variabila
endogena si reziduri) in jurul unei drepte de regresie, ceea ce este
comun cand avem heteroschedasticitate.
Valoarea tabelata din
distributia χ2
este 3.84. Cum Acalc>Atab spunem ca
exista cel putin un estimator care difera semnificativ de zero,
ceea ce implica prezenta heteroschedasticitatii. Am ales
modelul cu 8 orizonturi de timp, deoarece in urma estimarii mai multor
variante, acestui model ii corespundea valoarea cea mai mica pentru Akaike
Info Criterion. Interpretarea care poate fi data modelului in urma
acestui test este ca datele de acum 8 ani influenteaza
prezentul. Din graficul alaturat se observa si o dispunere in
forma de "palnie"a punctelor (dependenta dintre variabila
endogena si reziduri) in jurul unei drepte de regresie, ceea ce este
comun cand avem heteroschedasticitate.
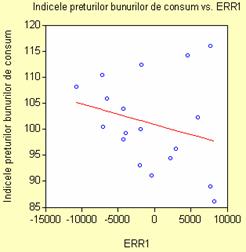 Urmatorul grafic arata ca
varianta variabilei reziduale este si in functie de indicele
preturilor bunurilor de consum (variabila exogena pentru modelul (1)), tot din forma de palnie a
distributiei.
Urmatorul grafic arata ca
varianta variabilei reziduale este si in functie de indicele
preturilor bunurilor de consum (variabila exogena pentru modelul (1)), tot din forma de palnie a
distributiei.
Deoarece am aratat anterior ca variabila
reziduala este in functie de variabila exogena, putem aplica testul Glejser. Estimez parametrii modelelor
de regresie:
|et|=a0 + a1PIB + ut,
|et|=a0 + a1*1/PIB + ut,
|et|=a0 + a1*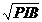 + ut,
+ ut,
dupa care testez daca estimatorul a1 difera
semnificativ de 0. Salvez valorile |et|
in seria abserr1 prin comanda:
genr abserr1=abs(err1)
Generez seriile sqr(PIB), 1/PIB
Modelul care poate fi acceptat la limita ca
relatie intre reziduri si Pib este cel de-al treilea, adica regresia
intre valorile absolute ale erorilor si radicalul PIB-ului. Estimatorii
sunt cei din tabelul alaturat. Se observa ca relatia nu
include termenul liber. Deci dependenta ar fi de forma |et|
= a1*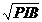 + ut , t=1..19
+ ut , t=1..19
Acesta este modelul care ofera cea mai corecta explicitare a
termenului liber.
In continuare am definit un model de regresie multipla, folosind
importurile ca variabila endogena, respectiv PIB-ul si IPC ca
variabile exogene:
IMPi = α +
β * PIBi + γ * IPC + εi , i=1..19
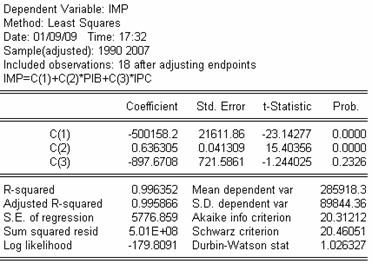 S-au estimat parametrii acestei regresii
in Eviews prin metoda celor mai mici patrate. Caracteristicile modelului
sunt prezentate in tabelul urmator. Ceea ce se poate citi la o prima
vedere este ca cele 2 variabile, PIB si IPC, au influente de
sens contrar asupra importurilor Frantei. Cresterea cu un milion de
euro a valorii PIB-ului implica cresterea valorii importurilor cu
0.636 milioane de euro in medie, iar cresterea indicelui preturilor
cu un procent determina scaderea importurilor cu -897.67 de milioane
de euro in medie.
S-au estimat parametrii acestei regresii
in Eviews prin metoda celor mai mici patrate. Caracteristicile modelului
sunt prezentate in tabelul urmator. Ceea ce se poate citi la o prima
vedere este ca cele 2 variabile, PIB si IPC, au influente de
sens contrar asupra importurilor Frantei. Cresterea cu un milion de
euro a valorii PIB-ului implica cresterea valorii importurilor cu
0.636 milioane de euro in medie, iar cresterea indicelui preturilor
cu un procent determina scaderea importurilor cu -897.67 de milioane
de euro in medie.
In continuare voi testa daca valoarea estimatorului pentru
coeficientul IPC difera semnificativ de zero.
Ipotezele testului statistic:
H0: γ=0;
H1: γ≠0;
Se
defineste statistica testului:
t=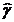 /σ
/σ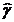 →t19-2
→t19-2
Conform datelor din tabelul de mai sus, tcalc=-1.244025, iar pentru un prag de semnificatie de 5%
si 17 grade de libertate tα/2,17=2.567.
Cum |tcalc|≤tα/2,17 se accepta ipoteza nula conform
careia panta dreptei de regresie nu difera semnificativ de zero, deci
nu poate fi inclusa in ecuatia de regresie.
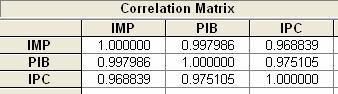
Urmaresc sa determin care sunt cauzele acestui rezultat. In
primul rand, am determinat matricea de
corelatie.
Se observa ca exista o corelatie puternica intre
variabila dependenta si fiecare din variabilele exogene, dar, in
acelasi timp, cele 2 variabile explicative sunt puternic corelate.
Datorita acestui fapt, in modelul de regresie definit anterior se manifesta
fenomenul de coliniaritate.
Voi testa acest lucru prin utilizarea testului
Klein. Din tabelul de regresie avem valoarea raportului de determinare R2=0.996.
Coeficientul de corelatie dintre PIB si IPC este r2pib/ipc=0,95.
Cum R2< r2pib/ipc intre perechile de variabile PIB si IPC
exista o dependenta liniara puternica, deci se
manifesta fenomenul de coliniaritate.
Am estimat anterior parametrii modelului format
din variabilele explicative PIB si IPC, modelul (3), dar si ai
modelului format din IMP, ca variabila endogena si IPC ca
variabila exogena, modelul (2). Aceasta reprezinta o modalitate
mecanica de eliminare a coliniaritatii.
Bibliografie
- "Econometrie",
T. Andrei, Editura Economica, Bucuresti, 2008
- "Introducere in
econometrie utilizand EViews", T. Andrei, Editura Economica, Bucuresti,
2008
- https://epp.eurostat.ec.europa.eu










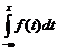 , unde
, unde 
 Pentru
a pune in evidenta
Pentru
a pune in evidenta 
 O
O
 Este
necesar
Este
necesar 









 Urmatorul grafic arata ca
varianta variabilei reziduale este si in functie de indicele
preturilor bunurilor de consum (variabila exogena pentru modelul (1)), tot din forma de palnie a
distributiei.
Urmatorul grafic arata ca
varianta variabilei reziduale este si in functie de indicele
preturilor bunurilor de consum (variabila exogena pentru modelul (1)), tot din forma de palnie a
distributiei. 
