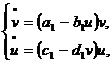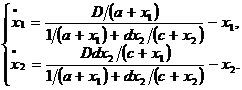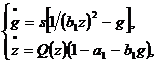Modele neliniare
Foarte multe relatii dintre variabilele
economice analizate in teoria economica sunt descrise ca avand o
forma neliniara. Varietatea relatiilor de acest tip
prezinta importanta atat din perspectiva estimarii (fiind
mai "aproape" de realitate) cat si din cea a prognozelor pe termen mediu
si, mai ales, lung. In continuare prezentam
cele mai importante modele neliniare din literatura de specialitate.
Determinarea pretului de
maximizare a profitului
Economistii
au elaborat un model de stabilire a pretului pentru ca acesta sa
contribuie la maximizarea profitului. Se pleaca de la ideea ca firma
respectiva cunoaste care sunt functiile cererii si costului
produsului in cauza. Daca in urma analizei de regresie ecuatia cererii are forma
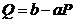
iar functia
costului ce descrie costul total C al producerii cantitatii Q intr-o
perioada de timp este de tip liniar:
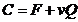
unde F este costul total
fix si v - costul variabil pe unitatea de produs si tinand cont
ca ecuatia venitului total V este:
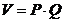
unde P - pretul practicat, Q - cantitatea
vanduta si profitul total Z
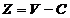
firma poate determina raportul dintre profit si
pret astfel
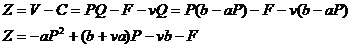
Deci, profitul total net este o ecuatie de gradul doi ce are ca
necunoscuta pretul. Maximul se atinge in punctul 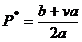
Modele GARCH pentru
analiza riscului de portofoliu
Modelele GARCH (G - generalizat, AR - autoregresiv, C -
conditional, H - heteroschedasticitate) au fost proiectate pentru a modela
serii economice ce nu urmeaza o distributie normala. In cadrul
acestor serii exista o abatere larga a valorilor extreme de la media
lor, unele fiind chiar asimetrice, ele prezentand si o evolutie
neuniforma a dispersiei de-a lungul perioadei de timp analizate. Primul
astfel de model a fost realizat de catre Robert Eagle in 1982. El cuprinde
o ecuatie pentru medie si una pentru dispersie, respectiv [11,pag.4]:
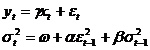
unde yt este variabila dependenta in perioada
curenta, xt - variabila independenta in perioada
curenta, 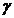 - coeficientul care
arata influenta variabilei independente asupra variabilei dependente,
- coeficientul care
arata influenta variabilei independente asupra variabilei dependente,
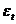 - termeni reziduali in
perioada curenta,
- termeni reziduali in
perioada curenta, 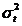 - dispersia variabilei
dependente in periada curenta,
- dispersia variabilei
dependente in periada curenta,  - constanta
ecuatiei dispersiei, α - coeficientul ARCH,
- constanta
ecuatiei dispersiei, α - coeficientul ARCH, 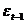 - termeni reziduali
din perioada precedenta,
- termeni reziduali
din perioada precedenta, 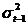 - dispersia variabilei
dependente in perioada precedenta, β - coeficient GARCH.
- dispersia variabilei
dependente in perioada precedenta, β - coeficient GARCH.
O
prezentare generalizata a acestui model poate fi gasita in
[31,pag.480].
Un alt model asemanator, a fost introdus de Nelson in 1991:
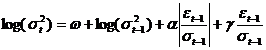
iar efectul de levier
poate fi testat prin testarea inegalitatii 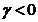 . Sa remarcam ca logaritmul
transfera modelul intr-unul neliniar.
. Sa remarcam ca logaritmul
transfera modelul intr-unul neliniar.
Modelul lui Goodwin de repartitie a
venitului
Sa
consideram o economie constand din muncitori si capitalisti
si sa presupunem ca muncitorii isi cheltuiesc toate
veniturile. Iata definitiile si relatiile care descriu
cadrul economic de lucru, in care preturile au fost normalizate la
unitate,
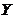 - productie
(realizarile economiei);
- productie
(realizarile economiei); 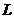 - munca
(identificata cu muncitorii);
- munca
(identificata cu muncitorii); 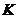 - capital investit
(identificat cu capitalistii);
- capital investit
(identificat cu capitalistii); 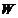 - salariu (identificat
cu salariul mediu lunar);
- salariu (identificat
cu salariul mediu lunar); 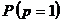 - pret produse
(bunuri);
- pret produse
(bunuri); 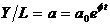 ,
,  - constanta -
productivitatea muncii;
- constanta -
productivitatea muncii; 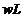 - venitul muncii
(venitul muncitorilor);
- venitul muncii
(venitul muncitorilor); 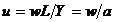 - partea muncii din
venit (partea muncitorilor din venit);
- partea muncii din
venit (partea muncitorilor din venit); 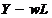 - venitul
capitalistilor;
- venitul
capitalistilor; 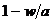 - partea
capitalistilor din venit;
- partea
capitalistilor din venit; 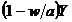 - economii;
- economii; 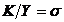 (constanti) -
raportul capital-productie;
(constanti) -
raportul capital-productie; 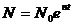 ,
, 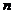 - constanti -
numar de muncitori;
- constanti -
numar de muncitori; 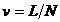 - rata de ocupare a
fortei de munca; Presupunand
ca investitiile
- rata de ocupare a
fortei de munca; Presupunand
ca investitiile 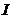 egaleaza
economiile, atunci cresterea stocului de capital
egaleaza
economiile, atunci cresterea stocului de capital 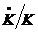 este de forma
este de forma 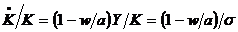 . Rata de crestere a stocului de capital este egala
cu rata de crestere a venitului
. Rata de crestere a stocului de capital este egala
cu rata de crestere a venitului 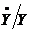 atunci cand raportul
capital-productie este constant. Cunoscand productivitatea muncii,
atunci cand raportul
capital-productie este constant. Cunoscand productivitatea muncii, 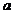 , se poate determina forta de munca
, se poate determina forta de munca 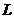 , necesara unei productii
, necesara unei productii 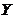 , prin formula
, prin formula 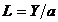 . Logaritmand si diferentiind aceasta
formula obtinem
. Logaritmand si diferentiind aceasta
formula obtinem 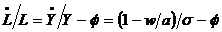 . Rezumand, avem urmatoarele rate de crestere
folosite in model:
. Rezumand, avem urmatoarele rate de crestere
folosite in model: 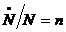 ,
, 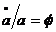 ,
, 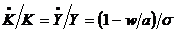 ,
, 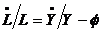 .
.
Variabilele
de stare in modelul lui Goodwin sunt: rata 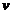 de ocupare a
fortei de munca si partea muncitorilor de venit
de ocupare a
fortei de munca si partea muncitorilor de venit  . Pentru a deduce ecuatiile in
. Pentru a deduce ecuatiile in 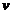 si
si  sa luam in
considerare doar evolutia ratei de ocupare a fortei de munca.
Logaritmand, diferentiind si efectuand calculele in expresia lui
sa luam in
considerare doar evolutia ratei de ocupare a fortei de munca.
Logaritmand, diferentiind si efectuand calculele in expresia lui 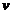 obtinem
obtinem 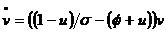 . Efectuand aceleasi prelucrari si in expresia
lui
. Efectuand aceleasi prelucrari si in expresia
lui  obtinem
obtinem 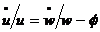 . Goodwin presupune ca salariul muncitorilor
evolueaza conform curbei standard a lui Philips, adica
. Goodwin presupune ca salariul muncitorilor
evolueaza conform curbei standard a lui Philips, adica 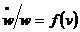 , in care
, in care 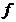 verifica
conditiile
verifica
conditiile 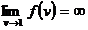 ,
, 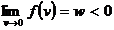 si
si 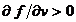 . Pentru simplicitate aceasta curba este
aproximata cu o linie
. Pentru simplicitate aceasta curba este
aproximata cu o linie 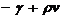 , deci evolutia partii din venit ce revine
muncitorilor capata expresia
, deci evolutia partii din venit ce revine
muncitorilor capata expresia 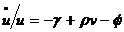 . De aici deducem imediat:
. De aici deducem imediat: 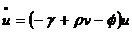 . Prin urmare tinand seama de toate ipotezele de mai
sus, evolutia ratei de ocupare a fortei de munca si a
partii din venit ce revine muncitorilor este descrisa de
s.e.d.o. de forma
. Prin urmare tinand seama de toate ipotezele de mai
sus, evolutia ratei de ocupare a fortei de munca si a
partii din venit ce revine muncitorilor este descrisa de
s.e.d.o. de forma
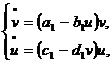
unde 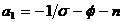 ,
, 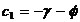 ,
, 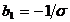 ,
, 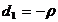 .
.
Problema
Cauchy pentru acest sistem poate fi asociata unui sistem dinamic
bidimensional cu neliniaritati patratice care depinde de patru
parametri reali. El este cunoscut sub numele
de modelul lui Goodwin. Acest model are pentru majoritatea valorilor parametrilor
doua echilibre, pentru o alta multime de masura
nula avand un singur echilibru. De asemenea el poseda si un
ciclu limita.
Modelul lui Denenbourg, de Palma si
Kahn (1979)
Acest
model descrie alegerea dinamica a unei modalitati de transport.
Fie 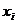 - numarul de
drumuri. Daca
- numarul de
drumuri. Daca 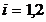 atunci modelul este
dat de
atunci modelul este
dat de 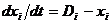 unde
unde 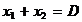 . Punand
. Punand 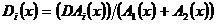 , dinamica depinde de fiecare
, dinamica depinde de fiecare 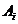 . Daca presupunem ca
. Daca presupunem ca 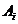 sunt
proportionale cu vitezele
sunt
proportionale cu vitezele 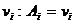 si ca nu
exista interactiuni intre cele doua (fie masina
si autobuz), atunci avem
si ca nu
exista interactiuni intre cele doua (fie masina
si autobuz), atunci avem 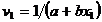 ,
, 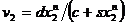 . Daca, in plus,
. Daca, in plus, 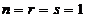 atunci dinamica
modalitatii de transport este data de
atunci dinamica
modalitatii de transport este data de
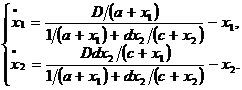
Model de crestere cu rata de
ajustare
Sistemul
descrie interactiunea dinamica dintre rata de crestere si
sistemul de asigurari sociale. Este considerat cazul in care viteza de ajustare
a ratei de crestere este optima dar nu prea rapida. El are forma
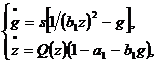
unde 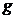 - rata de
crestere,
- rata de
crestere, 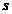 - viteza de ajustare,
- viteza de ajustare, 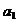 - viteza de consum,
- viteza de consum, 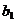 - cresterea
raportului capital-productie,
- cresterea
raportului capital-productie, 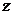 - valoarea totala
a productiei.
- valoarea totala
a productiei.
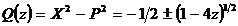
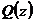 trebuie sa fie negativ cand
trebuie sa fie negativ cand 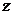 este pozitiv;
este pozitiv; 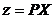
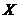 - capacitatea,
- capacitatea, 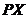 - valoarea totala a
capacitatii.
- valoarea totala a
capacitatii.


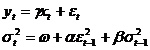
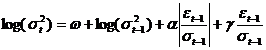
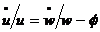 . Goodwin presupune ca salariul muncitorilor
evolueaza conform curbei standard a lui Philips, adica
. Goodwin presupune ca salariul muncitorilor
evolueaza conform curbei standard a lui Philips, adica