INTERSECTIA
SUPRAFETELOR CURBE
Generalitati
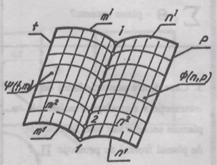
Se stie ca
doua suprafete 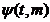 si
si 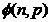 se intersecteaza, daca ele au puncte comune (fig.1).
Totalitatea punctelor (11 ,2, ,i) ce apartin ambelor
suprafete formeaza linia l de intersectie a
suprafetelor:
se intersecteaza, daca ele au puncte comune (fig.1).
Totalitatea punctelor (11 ,2, ,i) ce apartin ambelor
suprafete formeaza linia l de intersectie a
suprafetelor:
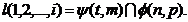
 Aceasta
linie poate fi plana sau spatiala. Ea poate fi de asemenea
curba sau poligonala (in cazul cind se intersecteaza
poliedrele). Ordinul liniei de intersectie este egal cu produsul ordinelor
suprafetelor. Constructia liniei de intersectie pe desene se
bazeaza pe proprietatea, ca punctele comune ale suprafetelor pot
fi la intersectia liniilor, care apartin acestor suprafete, in
scopul evidentierii acestor linii la construirea liniei de intersectie
se folosesc suprafete secante auxiliare.
Aceasta
linie poate fi plana sau spatiala. Ea poate fi de asemenea
curba sau poligonala (in cazul cind se intersecteaza
poliedrele). Ordinul liniei de intersectie este egal cu produsul ordinelor
suprafetelor. Constructia liniei de intersectie pe desene se
bazeaza pe proprietatea, ca punctele comune ale suprafetelor pot
fi la intersectia liniilor, care apartin acestor suprafete, in
scopul evidentierii acestor linii la construirea liniei de intersectie
se folosesc suprafete secante auxiliare.
Drept suprafete auxiliare pot fi
utilizate suprafetele plane ori sferice. Din aceste considerente la
construirea liniei de intersectie a suprafetelor se
diferentiaza metoda planelor auxiliare si metoda
sferelor auxiliare.
Metoda
planelor secante paralele
 Esenta
acestei metode consta in aceea ca suprafetele date
Esenta
acestei metode consta in aceea ca suprafetele date  si
si  sunt intersectate de
suprafete plane auxiliare
sunt intersectate de
suprafete plane auxiliare  care se aleg in
asa fel incit ele sa intersecteze suprafetele initiale
care se aleg in
asa fel incit ele sa intersecteze suprafetele initiale 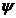 si
si  in linii drepte sau cercuri
in linii drepte sau cercuri 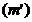 si
si 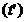 la intersectia
carora se obtin punctele 1 si 2 care apartin liniei de
intersectie l a suprafetelor (fig.2).
la intersectia
carora se obtin punctele 1 si 2 care apartin liniei de
intersectie l a suprafetelor (fig.2).
Asadar,
algoritmul de baza al gasirii punctelor comune ale suprafetelor
intersectate poate fi scris in felul urmator:
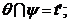
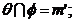
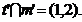
Procedura intersectiei suprafetelor se
repeta de atitea ori de cite este necesar pentru a obtine o linie cit
mai exacta.
Daca linia de
intersectie a suprafetelor date se construieste cu ajutorul
suprafetelor plane, care sunt paralele cu unul dintre planele de proiectie, aceasta
metoda se numeste metoda
 planelor auxiliare
secante paralele. Ea se utilizeaza in cazurile cind planele auxiliare intersecteaza
suprafetele date in linii drepte sau circumferinte.
planelor auxiliare
secante paralele. Ea se utilizeaza in cazurile cind planele auxiliare intersecteaza
suprafetele date in linii drepte sau circumferinte.
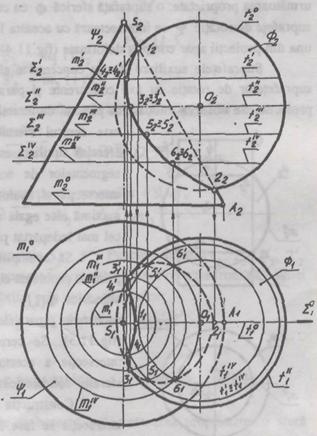
Sa exemplificam
utilizarea acestei metode in dubla proiectie ortogonala la intersectia unei suprafete conice 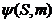 cu o suprafata sferica
cu o suprafata sferica 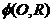 (fig.3).
(fig.3).
Punctele comune ale suprafetelor
se determina utilizind drept plane auxiliare ∑' Iv care sectioneaza
suprafata conica dupa circumferintele m', m', m1', m Iv si suprafata sferica - dupa circumferintele
t', t', t1', t Iv
 Intersectia acestor circumferinte determina punctele comune 3, 4, 5, 6
si 3',4',5',6'. Punctele de
baza 1 si 2 se gasesc la intersectia liniilor de contur t20
si S2A2 ale suprafetelor. Punctele 3 si 3', in care ecuatorul
sferei intersecteaza conul, se obtin cu ajutorul planului ||Π1 care se traseaza
prin centrul O2 al sferei. Aceste doua puncte situate pe
ecuatorul t' in proiectia orizontala impart linia de
intersectie a suprafetelor in doua parti:
vizibila (31-41-11-4 1-3 1)
si invizibila (31-61,-21-6'1-3 1). Din cauza simetriei fata
de planul de front pe
suprafata frontala doua ramuri ale liniei de intersectie
coincid.
Intersectia acestor circumferinte determina punctele comune 3, 4, 5, 6
si 3',4',5',6'. Punctele de
baza 1 si 2 se gasesc la intersectia liniilor de contur t20
si S2A2 ale suprafetelor. Punctele 3 si 3', in care ecuatorul
sferei intersecteaza conul, se obtin cu ajutorul planului ||Π1 care se traseaza
prin centrul O2 al sferei. Aceste doua puncte situate pe
ecuatorul t' in proiectia orizontala impart linia de
intersectie a suprafetelor in doua parti:
vizibila (31-41-11-4 1-3 1)
si invizibila (31-61,-21-6'1-3 1). Din cauza simetriei fata
de planul de front pe
suprafata frontala doua ramuri ale liniei de intersectie
coincid.
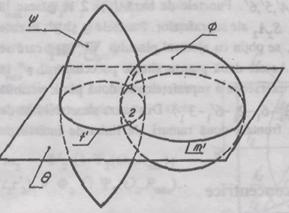
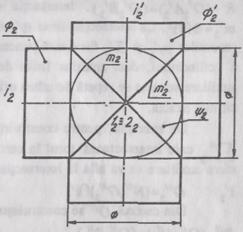
3. Metoda sferelor concentrice
Utilizarea
suprafetelor concentrice drept suprafete auxiliare pentru
determinarea curbelor de intersectie a doua suprafete de
rotatie are la baza urmatoarea proprietate: o
suprafata sferica  cu centrul in O situat
pe axa i a unei suprafete de
rotatie
cu centrul in O situat
pe axa i a unei suprafete de
rotatie 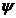 se intersecteaza cu aceasta in circumferinte (m, m'),
care in una din proiectii apar
complet deformate (fig. 4).
se intersecteaza cu aceasta in circumferinte (m, m'),
care in una din proiectii apar
complet deformate (fig. 4).
Suprafetele
auxiliare sferice concentrice sunt utilizate in cazul intersectiei
suprafetelor de rotatie cu axe concurente si paralele cu unul
dintre planele de proiectie. Se observa totodata ca punctul
de intersectie al axelor suprafetelor date este centrul sferelor
auxiliare. Raza minima a sferelor auxiliare este egala cu lungimea
maxima a segmentelor de normale trasate din punctul de intersectie al
axelor O pe suprafetele date. Raza maxima este egala cu
distanta dintre punctul O si cel mai indepartat punct al
liniei de intersectie.
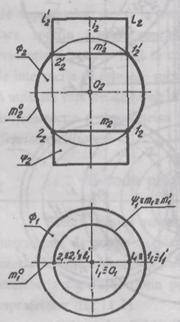 Sa
exemplificam cele expuse mai sus printr-o problema concreta. Fie
date doua suprafete cilindrice
Sa
exemplificam cele expuse mai sus printr-o problema concreta. Fie
date doua suprafete cilindrice 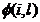 si
si 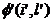 de rotatie cu axele concurente si paralele cu
planul frontal de proiectie (fig. 5). Se cere sa se
construiasca linia de intersectie a acestor suprafete, utilizind
metoda sferelor concentrice.
de rotatie cu axele concurente si paralele cu
planul frontal de proiectie (fig. 5). Se cere sa se
construiasca linia de intersectie a acestor suprafete, utilizind
metoda sferelor concentrice.
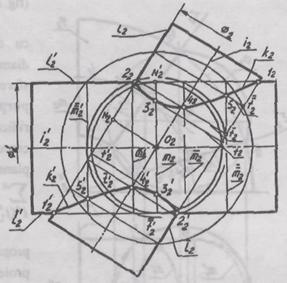
Constructia
grafica a proiectiei liniei de intersectie se face in felul
urmator: se determina
Centrul sferelor concentrice: 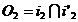 . Se gaseste
raza celei mai mici sfere
. Se gaseste
raza celei mai mici sfere 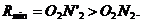 In suprafetele
date se inscrie prima sfera
In suprafetele
date se inscrie prima sfera 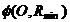 cu raza
cu raza 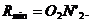 Se construiesc cercurile
de intersectie ale suprafetelor date cu sfera auxiliara:
Se construiesc cercurile
de intersectie ale suprafetelor date cu sfera auxiliara:
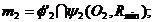
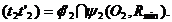
 Se gasesc punctele de
intersectie ale cercurilor, care apartin celor doua
suprafete cilindrice si suprafetei sferice:
Se gasesc punctele de
intersectie ale cercurilor, care apartin celor doua
suprafete cilindrice si suprafetei sferice:
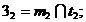
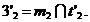
Se repeta procedura inscrierii
altei suprafete sferice cu R>Rmin si se
construiesc cercurile de intersectie ale suprafetelor:
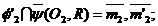
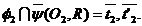
Se gasesc inca doua
puncte de intersectie ale cercurilor 4 si 4':
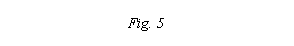
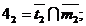
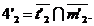
In mod analog se construiesc si
punctele 52 , 5' . Punctele de baza 12,22,
l'2, 2'2 se
afla la intersectia liniilor de contur ale suprafetelor date.
Proiectia frontala a liniei de intersectie a suprafetelor
se obtine prin unirea punctelor:
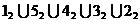 si
si 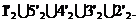
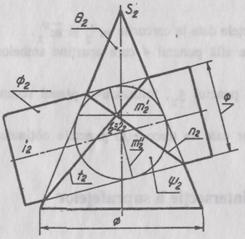
4. Metoda
sferelor excentrice
Utilizarea acestei
metode se bazeaza pe urmatoarea proprietate: o sfera 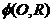 poate sa
intersecteze un tor
poate sa
intersecteze un tor 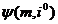 dupa
circumferinte (generatoarele m', m'), daca centrul sferei O se
gaseste in planul de simetrie ∑° al suprafetei (fig. 6).
dupa
circumferinte (generatoarele m', m'), daca centrul sferei O se
gaseste in planul de simetrie ∑° al suprafetei (fig. 6).
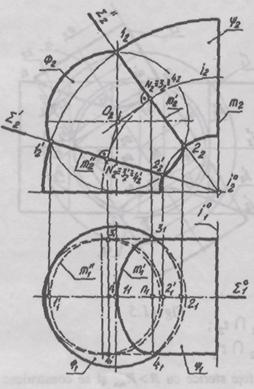 Segmentele (12,22),
(1 ' ) cu centrele in N2,
N' reprezinta
diametrele acestor cercuri. Centrul sferei O2 se
gaseste la intersectia perpendicularelor N2O2 si
N'2O2 ridicate
din centrele N2 si N' Planele cercurilor m' si m' se gasesc
in planele proiectante ∑'┴Π2
si ∑'' Π2
trasate prin axa de rotatie i0(i10,i20)
a torului.
Segmentele (12,22),
(1 ' ) cu centrele in N2,
N' reprezinta
diametrele acestor cercuri. Centrul sferei O2 se
gaseste la intersectia perpendicularelor N2O2 si
N'2O2 ridicate
din centrele N2 si N' Planele cercurilor m' si m' se gasesc
in planele proiectante ∑'┴Π2
si ∑'' Π2
trasate prin axa de rotatie i0(i10,i20)
a torului.
Sa examinam
utilizarea acestei proprietati a sferei la construirea
proiectiilor liniei de intersectie a suprafetelor.
Fie date torul 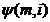 si suprafata cilindrica
si suprafata cilindrica 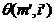 axele arora se
gasesc intr-un plan de front (fig. 7). Se cere sa se
construiasca linia de intersectie a suprafetelor:
axele arora se
gasesc intr-un plan de front (fig. 7). Se cere sa se
construiasca linia de intersectie a suprafetelor:
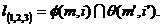
Punctele comune ale suprafetelor
pot fi gasite in felul urmator: stiind, ca axele i' si i ale
suprafetelor se afla intr-un plan de front, se gasesc punctele
de baza 12 si 22 ca rezultat al
intersectiei liniilor de contur ale suprafetelor. Prin axa i20
se traseaza un plan auxiliar ∑ la intersectia
caruia cu suprafata torica obtinem cercul m2'
cu diametrul A2'B'
 Din centrul N'2
al cercului
se coboara o perpendiculara pe planul cercului pina la
intersectia ei cu axa de rotatie i a cilindrului (se
obtine centrul O'2 ).
Din centrul N'2
al cercului
se coboara o perpendiculara pe planul cercului pina la
intersectia ei cu axa de rotatie i a cilindrului (se
obtine centrul O'2 ).
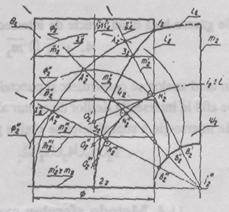 Din centrul O'2, se
construieste suprafata sferica
Din centrul O'2, se
construieste suprafata sferica 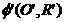 cu raza
cu raza 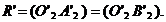 Intersectia
sferei
Intersectia
sferei 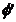 cu torul
cu torul 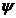 formeaza cercul m'2=
formeaza cercul m'2=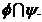 La intersectia sferei
La intersectia sferei 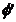 cu cilindrul
cu cilindrul 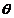 obtinem
cercul
obtinem
cercul 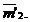 Intersectia cercurilor
Intersectia cercurilor 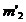 si
si 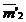 formeaza punctul 32
care apartine atit proiectiei torului cit si a cilindrului, deci apartine liniei de
intersectie. Procedura construirii sferelor auxiliare secante se repeta de
atitea ori, de cite este necesar pentru a obtine o linie cit mai
exacta.
formeaza punctul 32
care apartine atit proiectiei torului cit si a cilindrului, deci apartine liniei de
intersectie. Procedura construirii sferelor auxiliare secante se repeta de
atitea ori, de cite este necesar pentru a obtine o linie cit mai
exacta.
 De exemplu, pentru
construirea punctlui 42
se traseaza prin i20 planul ∑ care
intersecteaza torul in cercul m'. Proiectia centrului celei de-a doua
sfere auxiliare se va afla la intersectia perpendicularei N'2Q'2
cu axa cilindrului
De exemplu, pentru
construirea punctlui 42
se traseaza prin i20 planul ∑ care
intersecteaza torul in cercul m'. Proiectia centrului celei de-a doua
sfere auxiliare se va afla la intersectia perpendicularei N'2Q'2
cu axa cilindrului
i20: 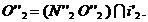
Din centrul O'
se construieste sfera auxiliara 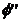 cu raza :
cu raza :
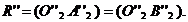
Aceasta sfera va
intersecta suprafetele date in cercurile 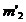 si
si 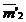
La intersectia
acestor cercuri se afla punctul 4 care apartine ambelor
suprafete: 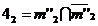
In mod analog se
construieste si punctul 52,
folosindu-se planul secant auxiliar ∑'''┴
Linia de
intersectie a suprafetelor date va trece prin punctele obtinute:
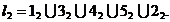
5 Cazuri
particulare de intersectie a suprafetelor de ordinul doi
 Intrucit
suprafetele de ordinul doi sunt algebrice, linia de intersectie este
o curba algebrica (in caz general - o linie spatiala).
Aceasta curba este de ordinul patru, fiindca ordinul liniei de
intersectie este egal cu produsul ordinelor suprafetelor, in practica
construirii desenelor industriale se imilnesc cazuri cind linia de
intersectie a suprafetelor de ordinul doi se descompune in citeva
linii de ordine inferioare.
Intrucit
suprafetele de ordinul doi sunt algebrice, linia de intersectie este
o curba algebrica (in caz general - o linie spatiala).
Aceasta curba este de ordinul patru, fiindca ordinul liniei de
intersectie este egal cu produsul ordinelor suprafetelor, in practica
construirii desenelor industriale se imilnesc cazuri cind linia de
intersectie a suprafetelor de ordinul doi se descompune in citeva
linii de ordine inferioare.
O
importanta deosebita are descompunerea liniei de
intersectie de ordinul patru in doua curbe plane de ordinul doi. In
continuare sunt prezentate unele cazuri mai des intilnite in practica.
l. Daca doua
suprafete de ordinul doi se intersecteaza dupa o curba
plana de ordinul doi, atunci ele se intersecteaza inca dupa
o curba tot de ordinul doi.
 Justetea legii
reiese din conditia ca suma ordinelor liniilor, in care se descompune
linia de intersectie, este egala cu ordinul acestei linii, in cazul
dat linia de intersectie este de ordinul patru. Daca o parte din
aceasta linie este o curba de ordinul doi, inseamna ca a
doua parte trebuie sa fie de asemenea de ordinul doi. De exemplu,
daca o suprafata cilindrica de ordinul doi
Justetea legii
reiese din conditia ca suma ordinelor liniilor, in care se descompune
linia de intersectie, este egala cu ordinul acestei linii, in cazul
dat linia de intersectie este de ordinul patru. Daca o parte din
aceasta linie este o curba de ordinul doi, inseamna ca a
doua parte trebuie sa fie de asemenea de ordinul doi. De exemplu,
daca o suprafata cilindrica de ordinul doi  intersecteaza o suprafata sferica
intersecteaza o suprafata sferica 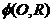 dupa un cerc m
atunci ea se intersecteaza cu sfera inca dupa un cerc m'
(vezi fig. 4-7).
dupa un cerc m
atunci ea se intersecteaza cu sfera inca dupa un cerc m'
(vezi fig. 4-7).
Daca doua suprafete  si
si 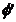 de ordinul
doi au contact in doua puncte (1,2), atunci linia lor de
intersectie se descompune in doua curbe plane de ordinul doi, planele
carora trec prin dreapta care uneste punctele de contact (fig. 8).
de ordinul
doi au contact in doua puncte (1,2), atunci linia lor de
intersectie se descompune in doua curbe plane de ordinul doi, planele
carora trec prin dreapta care uneste punctele de contact (fig. 8).
 Fie dati
Fie dati 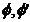 - doi cilindri cu
diametre egale, unde 1,2 sunt puncte de contact ale cilindrilor, in
acest caz se obtin doua linii de intersectie:
- doi cilindri cu
diametre egale, unde 1,2 sunt puncte de contact ale cilindrilor, in
acest caz se obtin doua linii de intersectie: 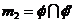 si
si 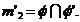 Liniile m,m' reprezinta doua
curbe de ordinul doi (elipse).
Liniile m,m' reprezinta doua
curbe de ordinul doi (elipse).
Daca
doua suprafete  si
si 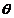 (fig. 9) de
ordinul doi sunt circumscrise unei suprafete de ordinul doi
(fig. 9) de
ordinul doi sunt circumscrise unei suprafete de ordinul doi 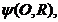 atunci ele se
intersecteaza dupa curbe plane (t,n) de
ordinul doi. Planele acestor curbe trec prin dreapta (1,2), care
uneste punctele de intersectie ale liniilor de contact.
atunci ele se
intersecteaza dupa curbe plane (t,n) de
ordinul doi. Planele acestor curbe trec prin dreapta (1,2), care
uneste punctele de intersectie ale liniilor de contact.
Intrebari
de control
Ce se numeste
linie de intersectie a suprafetelor?
Prin ce metode se efectueaza
constructia liniei de intersectie a suprafetelor?
In ce consta
esenta metodei planelor secante paralele?
In ce consta
esenta metodei sferelor concentrice?
Ce proprietate a
sferei este pusa la baza utilizarii sferei ca suprafata auxiliara
pentru constructia liniilor de intersectie?
In ce cazuri se
utilizeaza metoda planelor auxiliare?
In ce cazuri se
utilizeaza metoda sferelor concentrice?
Cum se determina
ordinul liniei de intersectie a suprafetelor?
Care sunt cazurile
particulare de intersectie a suprafetelor de ordinul doi?






 Se gasesc punctele de
intersectie ale cercurilor, care apartin celor doua
suprafete cilindrice si suprafetei sferice:
Se gasesc punctele de
intersectie ale cercurilor, care apartin celor doua
suprafete cilindrice si suprafetei sferice: 


