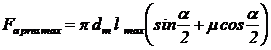ASAMBLARI INTRE BUTUCI SI ARBORI
1. Notiuni genarale
Utilizare. Asamblarile intre butuci si arbori sunt asamblari
demontabile formate dintr-o piesa cuprinzatoare (butuc) si o piesa cuprinsa
(arbore). Ele sunt utilizate pentru fixarea rotilor sau a altor organe de
masini pe arbori in scopul transmiterii momentelor de torsiune, si/sau a
fortelor axiale, asigurarea impotriva deplasarilor relative axiale sau
unghiulare si ca elemente de siguranta la suprasarcini sau inpotriva desfacerii
in timpul functionarii.
Clasificare. Asamblarile intre butuci si arbori se clasifica in
principal dupa criteriile indicate in fig. 1:
natura
elementului intermediar de imbinare;
modul de
transmitere a sarcinilor.
Recomandari de utilizare. Alegerea si utilizarea unui anume tip de asamblare
dintre cele prezentate in fig. 1 depinde de:
natura si
caracterul incarcarii (forta sau moment de torsiune, static sau dinamic);
tipul
asamblarii (fix sau cu posibilitati de deplasare axiala sau unghiulara);
frecventa
demontarii;
alte cerinte
functionale si constructive (importanta, destinatie, gabarit, acces, pret de
cost, tehnologie de fabricatie etc).
In tab. 1 sunt indicate cateva
recomandari privind utilizarea acestor asamblari.
2. Asamblari prin forma
Definire. Asamblari
prin forma folosesc pentru transmiterea sarcinilor fie elemente intermediare
(pene, stifturi), fie elemente care fac corp comun cu piesele asamblate,
cuplate reciproc (caneluri, profile speciale), fara sa apara forte de
strangere. Aceste elemente sunt solicitate, dupa caz, la rasucire, forfecare,
strivire (contact) sau incovoiere.
Materiale. Elementele intermediare de asamblare se fabrica in
genaral din oteluri carbon (OL50, OL60) fara tratamente termice, sau oteluri
carbon de calitate pentru imbunatatire (OLC35, OLC45). Pentru asamblari ce
lucreaza in conditii deosebite de mediu (agresiv) sau in cazul unor gabarite
impuse se pot utiliza si alte materiale: oteluri inoxidabile, refractare,
oteluri cu caracteristici superioare sau aliaje neferoase.
2.1. Asamblari cu stifturi si
bolturi
Stifturile si bolturile sunt organe
de masini ce servesc constituirea asamblarilor demontabile cu utilizari dintre
cele mai diverse.
Stifturile
sunt in general organe de masini standardizate si foarte variate ca forma:
stifturi cilindrice
netede (STAS 1599-80), stifturi cilindrice crestate (STAS 7464-71), stifturi
filetate cu locas hexagonal STAS 10423-80, (cu varf tesit STAS 5173-69, cu varf
conic STAS 5123-69, cu cep STAS 5171-69), stifturi filetate cu cap de surubelnita (varf tesit, STAS 4847-69, varf conic, STAS 4771-69, cu cep,
STAS 4867-69), stifturi filetate cu autoblocare (STAS 10420-76, STAS 10421-76
etc), stifturi conice netede (STAS 3436-80), stifturi conice crestate (STAS
7303-80), stifturi elasice (STAS 9729/1,2,3-80).
Bolturile sunt de forma
cilindrica: bolturi cu cap (STAS 5754/1,2-80) si bolturi fara cap (STAS
5756-73).
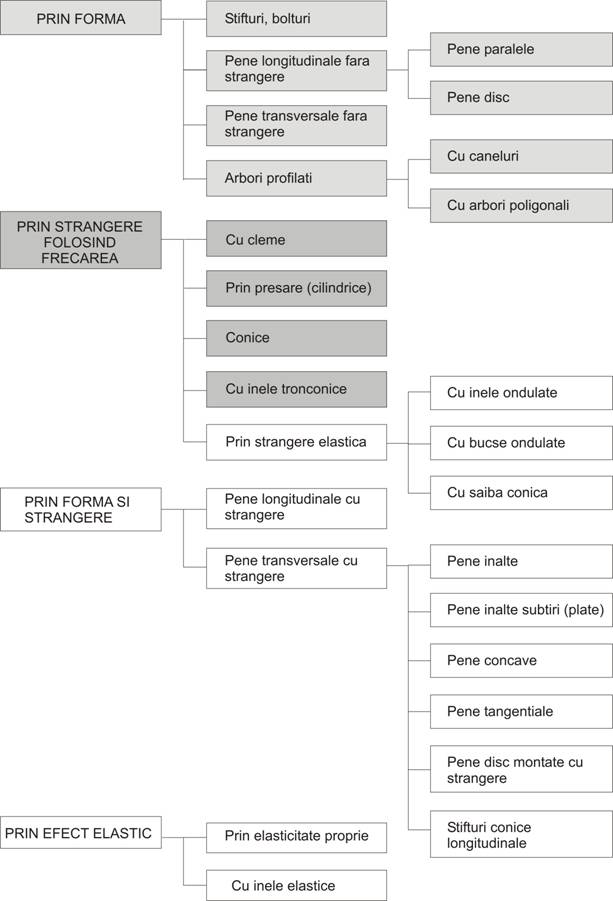
Fig. 1. Clasificarea asamblarilor arbore-butuc
Tabelul 1
Recomandari
de utilizare pentru diversele asamblari butuc-arbore
|
Recomandari
|
Asamblari
prin strangere
|
Asamblari
prin forma
|
Asamblari
prin forma si strangere
|
|
Momente de rasucire mici
|
Bratara elastica
Inele ondulate
Bucsa ondulata
|
Stift transversal
Stift longitudinal
Pana disc
Pana paralela
|
Pana concava
|
|
Momente de rasucire unidirectionale
|
Bratara elastica
Strangere proprie
Pana tangentiala
Inele ondulate
|
Stift transversal
Stift longitudinal
Pana paralela
|
Pana concava
|
|
Momente de rasucire cu schimbare de sens
|
Inele ondulate
|
Pana paralela
|
Pana concava
|
|
Momente de rasucire mari cu
schimbare de sens sau cu socuri
|
Strangere proprie
Strangere pe con
Cu inel tronconic
|
Arbori profilati (caneluri si arbori triunghiulari)
|
Pana inclinata
Pana tangentiala
|
|
Arbore scurt, momente mari de rasucire
|
Strangere pe con
Strangere cu inel tronconic
|
Arbori profilati (caneluri dreptunghiulare si triunghiulare, arbori
poligonali)
|
|
|
Asamblare cu
deplasare axiala (butuc sau arbore deplasabil)
|
|
Pana paralela lunga
Caneluri dreptunghiu-lare
|
|
|
Butuci usor demontabili
|
Bratara elastica
Strangere proprie
Strangere pe con
Cu inel tronconic
Cu inele si bucse ondulate
Cu inele elastice
|
Pana paralela,
arbori profilati (cu caneluri triunghiulare)
|
Pene inclinate (inalte,
tangentiale concave)
|
|
Arbore neted
|
Diverse imbinari cu strangere
|
|
Pana concava
|
|
Pentru pozitionarea usoara a
butucului in sens circular
|
Bratara elastica
Strangere pe con
Cu inel tronconic
Cu inele si bucse ondulate
Cu saibe conice
|
Caneluri triunghiulare
|
Pana concava
|
|
Asamblari cu arbore tubular
|
Cu inele tronconice
Strangere proprie
|
Caneluri dintate
|
|
Materiale. Stifturile si bolturile
standardizate se fabrica din materiale indicate in standardele respective
(OL50, OL60, OLC35). Stifturile elastice se executa din banda de otel de arc
OLC70A, iar stifturile filetate din materiale cu sr
= (650.800) Mpa eventual cu
tratamente termice de durificare superficiala in zona de varf (42.45 HRC).
Asamblarile cu stifturi si bolturi
servesc pentru:
transmiterii
de sarcini relativ mici (stifturi
lobgitudinale si transversale);
realizarea de
articulatii (stifturi cilindrice, bolturi);
asigurare si
fixare (stifturi cilindrice sau conice stemuite, stifturi filetate);
asigurarea
pozitiei reciproce corecte in cazul montarilor si demontarilor repetate;
ca elemente de
siguranta (stifturi filetate la asamblarile cu pana sau la asamblarile
filetate).
Datorita marii varietati de forme constructive a stifturilor si
bolturilor exista o mare diversitate de asamblari de acest tip. In fig.2 sunt
indicate cateva exemple de utilizare.
Stiftul transversal (fig. 2,a). Tensiunea nominala de forfecare din
stift este:
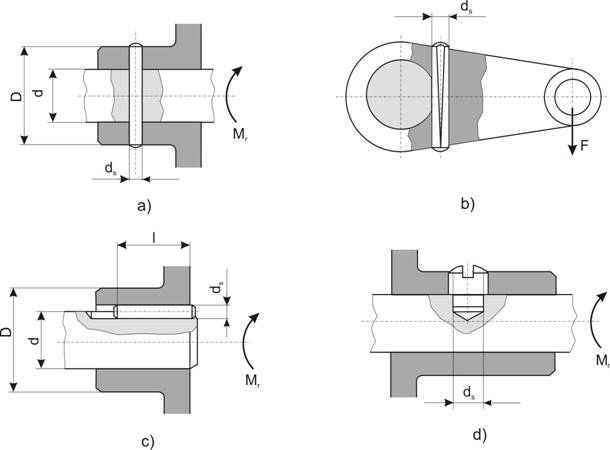
Fig. x.2. Asamblari de forma prin stifturi:
a)-stift transversal; b)-stift transversal
elastic; c)-stift longitudinal; d)-stigt transversal filetat
|
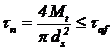
|
(1)
|
in care: taf
- tensiunea admisibila la forfecare; taf = (0,2.0,3)s0,2
s0,2
- limita de curgere a materialului stiftului.
Pentru
stifturile transversale elastice (fig. 2,b)., in standarde se indica
forta de forfecare minima, Ff pentru o sectiune sau doua sectiuni de
forfecare, astfel incat conditia de rezistenta se formuleaza altfel:
pentru o
sectiune de forfecare: 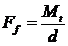
pentru o
sectiune de forfecare: 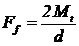
Coeficientul
de siguranta al imbinarii este: 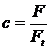
Tensiunile
de contact nominale (valori medii) sunt:
intre stift si butuc:
|
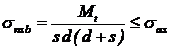
|
(2)
|
in care: sas -
tensiunea admisibila la strivire a materialului stiftului; 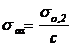 ; c = 2.4, pentru asamblari fixe. Pentru asamblari mobile,
din conditia de ungere: sas = (10.13) Mpa
; c = 2.4, pentru asamblari fixe. Pentru asamblari mobile,
din conditia de ungere: sas = (10.13) Mpa
intre stift si arbore:
|
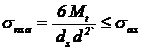
|
(3)
|
Stifult longitudinal (fig. 2,c). Tensiunea nominala de forfecare din
stift este:
|
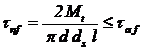
|
(4)
|
Tensiunile
de contact nominale (valori medii) sunt:
|
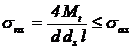
|
(5)
|
Stift transversal
filetat nepatruns (fig. 2,d).
Tensiunea nominala de forfecare din stift este:
|
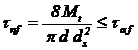
|
(6)
|
Boltul de articulatie
(fig. 3) este cel mai utilizat element pentru astfel de imbinari. El este
solicitat la forfecare, strivire si incovoiere.
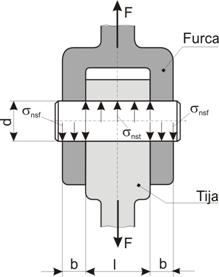
Fig. 3.
Asamblare de forma prin bolt (de articulatie)
Tensiunea nominala de
forfecare din bolt:
|
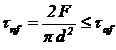
|
(7)
|
Tensiunea nominala de
contact:
dintre bolt si tija:
|
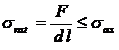
|
(8)
|
dintre bolt si
furca:
|
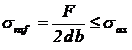
|
(9)
|
Tensiunea nominala de
incovoiere tinand seama de sarcina uniform distribuita:
|
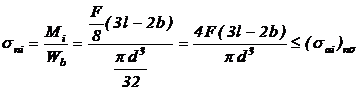
|
(10)
|
in care: Mi - momentul
incovoietor maxim;
Wb - modulul de rezistenta
axial al boltului;
(sai )ns -
tensiunea admisibila la incovoiere a materialului boltului pentru un anume grad
de solicitare.
Stifturile
de siguranta sunt folosite la asamblari care trebuie sa transmita o anumita
solicitare (forta sau moment de torsiune), si care la depasirea acesteia se
distrug anuland asamblarea. Cele mai utilizate asamblari cu stift de siguranta
sunt acelea la care stiftul se foarfeca. Pentru a se controla mai bine
solicitare (de forfecare pura) stiftul se intriduce in doua bucse care sa poata
prelua solicitarea de contact, iar suprafetele de separatie ale acestora,
situate la limita elementelor asamblate sa solicite stiftul numai la forfecare
(fig. 4) si (fig. 5). Aceste tipuri de asamblari se utilizeaza la cuplajele de
siguranta (limitatoare de moment de torsiune). In unele cazuri stiftul este
prevazut cu crestatura in zona de forfecare pentru a amorsa ruperea.
Bucsele
se verifica la solicitarea de contact, iar stiftul la solicitarea de forfecare:
|
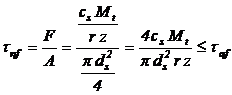
|
(11)
|
in care: F - forta de forfecare pe un stift;
A - aria de forfecare a stiftului;
cs - coeficient de sarcina;
cs = (1.3); uzula se adopta cs = 1,25.
taf
- tensiunea admisibila la forfecare; taf = K sr (coeficientul K are valori date in tab. 2).
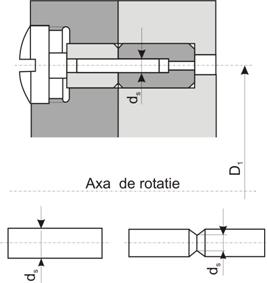
Fig. 4.
Cuplaj de siguranta cu flanse
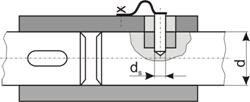
Fig. 5. Cuplaj de siguranta cu manson
Tabelul
2
Stifturi de siguranta. Valorile coeficientului K
|
Diametrul
stiftului,
ds,[mm]
|
Stift neted
|
Stift cu
crestatura
|
|
Alungirea la
rupere a materialului:
|
|
12 . 17 %
|
20 . 22 %
|
|
2.3
|
0,80 . 078
|
0,81 .0,80
|
0,80. 0,90
|
|
4.5
|
0,72 . 0,68
|
0,76 . 0,75
|
0,80. 0,90
|
Ajustajele recomandate pentru:
asamblari cu stifturi: pentru arbore-butuc (H11/h11
sau H7/m6), pentru centrari (H7/m6), pentru stifturi elastice, la
alezaje (H12), pentru stifturi crestate, alezaj (H8, H9, H11);
asamblari cu
stifturi de siguranta pentru stift-bucsa (H11/h11);
asamblarile cu
bolturi, in dunctie de destinatie.
2.2. Asamblari cu pene transversale
fara strangere
Penele transversale fara strangere
servesc pentru asamblarea a doua piese coaxiale. Pana are o forma
paralelipipedica in sectiune avand muchiile rotunjita (fig. 6,a). Pana este
montata cu jos in locasurile
practicate in piesele de imbinat (fig. 6,b,c).
Materiale.
Pentru penele transversale fara strangere se folosesc oteluri carbon (OL50,
OL60, OL70) fara tratamente termice, sau oteluri carbon de calitate pentru
imbunatatire (OLC35, OLC45), sau dupa caz, oteluri aliate cu caracteristici
superioare de rezistenta.
Calculul
de verificare. Penele transversale fara strangere sunt solicitate la:
incovoiere:
|
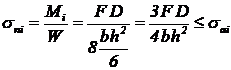
|
(12)
|
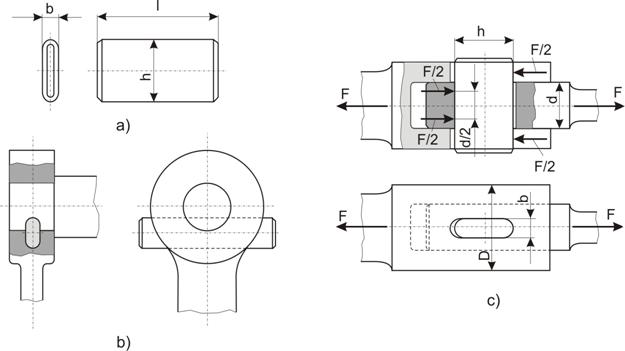
Fig. 6. Asamblari cu pene transversale fara
strangere;
a)-pena transversale fara strangere;
b)-asigurarea a doua piese imbinate; c)-asamblare tip tija-manson
forfecare:
|
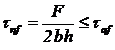
|
(13)
|
strivire
(contact):
intre manson-pana:
|
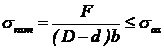
|
(14)
|
intre
arbore-pana:
|
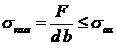
|
(15)
|
in care: Mi - momentul
incovoietor maxim;
W - modulul de rezistenta axial al
penei;
Tensiunile admisibile de mai sus se pot determina
aproximativ cu relatiile:
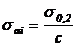 ; c = 1,45.1,80
; c = 1,45.1,80
taf = (0,2.0,3) s0,2
sas = 0,8 s0,2
2.3.
Asamblari cu pene longitudinale fara strangere
Penele longitudinale fara
strangere sunt de forma
paralelipipedica (exceptie fac penele disc) cu capelele rotunde sau drepte. Ele
se introduc in canale speciale practicate in arbori si butuci realizand o
solidarizare a acestora la rasucire. Prin aceste tipuri de asamblari se transmit numai momente de torsiune (datorita
sectiunii constante ale penelor, functie de ajustajul dintre arbore-butuc si
pana-butuc pot avea loc deplasari axiale relative intre arbore si butuc).
Transmiterea momentelor de torsiune se efectueaza prin zonele de contact
laterale ale penelor cu peretii canalelor din arbore si butuc.
Materiale.
Pentru penele longitudinale fara strangere se foloseste oteluri carbon (OL50,
OL60) fara tratamente termice, sau oteluri carbon de calitate pentru
imbunatatire (OLC35, OLC45) si mai rar oteluri aliate cu caracteristici
superioare de rezistenta.
Formele constructive ale penelor
longitudinale fara strangere sunt indicate in (fig. 7) si sunt de doua feluri:
pene
paralele cu capetele rotunde sau drepte, fig. 7,a,b de forma paralelipipedica avand uneori gauri de fixare in
arbori. Tipodimensiunile penelor paralele cu destinatie generala sunt tipizate
in STAS 1004-81, STAS 1006-90, STAS
9501-81, STAS 12933-91; penele paralele cu destinatie speciala (masini unelte,
prese) fac obiectul altor standarde sau norme speciale;
pene disc (fig. 7,c), STAS 1012-77 avand forma unei prisme
su sectiunea segment de cerc.
Penele paralele, datorita simplitatii lor
constructive se folosesc in cazul in care se pun conditii de coaxialitate
concomitent cu alegerea corespunzatoare a ajustajului arbore-butuc-pana sau
cand se impun deplasari axiale relative a butucului fata de arbore. Atunci cand
conditiile de montaj nu permit montarea unei pene de o anumita lungime
(determinata din conditia de de rezistenta), se pot utiliza doua sau trei pene
montate la 1200. In tab. 3 si tab. 4 se dau extrase din standarde privitoare la tipodimensiunile
penelor paralele si disc precum si abaterile dimensionale si ajustajele
recomandate.
Pentru a impiedica deplasarea axiala
a butucului fata de arbore se prevad si alte sisteme de fixare (umeri de
arbori, umeri rezultati prin solidarizarea unei bucse cu stifturi in arbore,
inele de fixare, sau un ajustaj corespunzator butuc-pana).
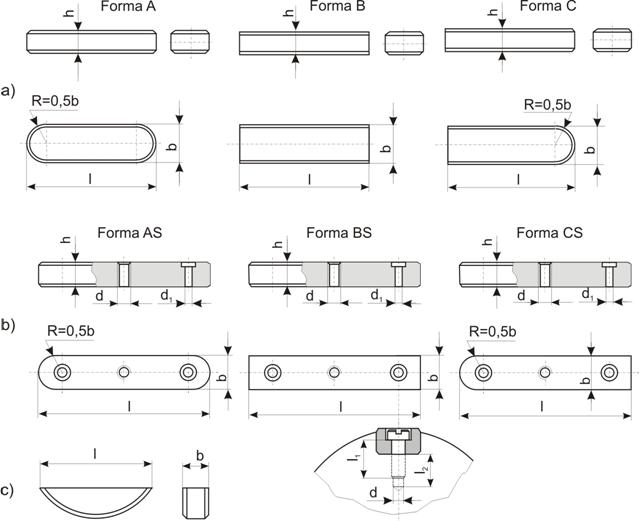
Fig. 7 Pene longitudinale
fara strangere:
a)-pene paralele simple; b)-pene
paralele cu elemente de fixare in arbore; c)-pene disc
Alegerea tipului de pana paralela (cu
capete rotunde sau drepte) se face in functie de posibilitatile tehnologice de
executie sau de conditiile de montaj. Cele mai frecvent folosite sunt insa
penele paralele cu capetele rotunde.
Pene paralele de lungimi mari
(penele-ghidaj), ce depasesc cu mult lungimea butucului se fixeaza de arbori
prin suruburi pentru se evita smulgerea penei din canal datorita apasarilor
laterale sau incovoierii ansamblului, cu toate ca acesta solutie reduce
rezistenta la oboseala a arborelui.
Penele disc se utilizeaza pentru
transmiterea momentelor de torsiune mici, ca pene de fixare sau atunci cand
arborele in zona asamblarii are rotiri mari.
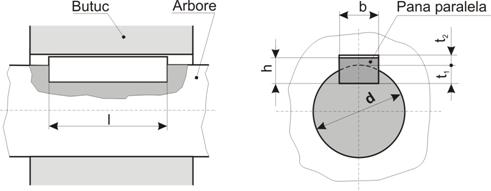
Elemente de calcul. Pana paralele este ajustata pe suprafetele
laterale ale canalului din butuc si arbore, fara strangere radiala si transmite
momentul de torsiune prin contactul avut pe fetele laterale ale canalelor
amintite (fig. 8). Calculul penei se rezuma la alegerea din standarde a
sectiunii penei b h in functie de
diametrul arborelui, d si consta in doua etape:
Tabelul 3
Pene paralele. Dimensiuni de pene si sectiuni de
canale (extras din STAS 1004-81)
|
Diametrul
nominal, d,
[mm]
|
Dimensiunile
penei, [mm]
|
Dimensiunile
canalului, [mm]
|
|
Sectiunea
|
Lungimea, l***)
|
Adancimea
|
b, ajustaj normal
|
|
b **)
|
h
|
t1
|
t2
|
In arbore
(N9)
|
In arbore
(Js9)
|
|
Nominal
|
Abateri, (h9)
|
Nominal
|
Abateri
|
Minim
|
Maxim
|
|
10 *) 12
|
4
|
0
- 0,030
|
4
|
0
0.030
|
8
|
45
|
2,5
|
1,8
|
0
- 0,030
|
0,015
|
|
12 17
|
5
|
5
|
10
|
56
|
3,0
|
2,3
|
|
17 22
|
6
|
6
|
14
|
70
|
3,5
|
2,8
|
|
22 30
|
8
|
0
- 0,036
|
7
|
0
0.090
|
18
|
90
|
4,0
|
3,3
|
0
- 0,036
|
0,018
|
|
30 38
|
10
|
8
|
22
|
110
|
5,0
|
3,3
|
|
38 44
|
12
|
0
- 0,043
|
8
|
28
|
140
|
5,0
|
3,3
|
0
- 0,043
|
0,022
|
|
44 50
|
14
|
9
|
36
|
160
|
5,5
|
3,8
|
|
50 58
|
16
|
10
|
45
|
180
|
6,0
|
4,3
|
|
58 65
|
18
|
11
|
50
|
200
|
7,0
|
4,4
|
|
65 75
|
20
|
0
- 0,052
|
12
|
0
0.110
|
56
|
220
|
7,5
|
4,9
|
0
- 0,052
|
0,026
|
|
75 85
|
22
|
14
|
63
|
250
|
9,0
|
5,4
|
|
85 95
|
25
|
14
|
70
|
280
|
9,0
|
5,4
|
|
95 110
|
28
|
16
|
80
|
320
|
10,0
|
6,4
|
|
110 130
|
32
|
0
- 0,062
|
18
|
90
|
360
|
11,0
|
7,4
|
0
- 0,062
|
0,026
|
|
130 150
|
36
|
20
|
0
0.130
|
100
|
400
|
12,0
|
8,4
|
|
150-170
|
40
|
22
|
110
|
450
|
13,0
|
9,4
|
|
* Se
include prima valoare, se exclude a doua valoare (exemplu: inclusiv 10
exclusiv 12).
** Pentru canal abaterile sunt:
ajustaj
liber: arbore h9; butuc D10;
ajustaj
presat: arbore si butuc P9.
*** Lungimile
nominale sunt: 6; 8; 10; 12; 14; 16; 18; 20; 22; 25; 28; 32; 36; 40; 45; 50;
56; 63; 70;
80; 90; 100; 110; 125; 140; 160; 180; 200;
220; 250; 280; 320; 360; 400; 450; 500.
|
1. Dimensionarea penei din
conditia de rezistenta la contact (conditie mai severa), cand se considera ca
adancimea canalelor in butuc si arbore sunt egale, (t1 t2), rezultand lungimea necesara,
dupa care se adopta lungimea penei standardizata:
|
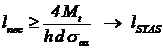
|
(16)
|
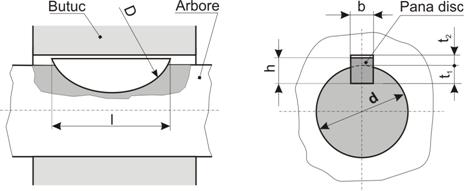
Tabelul 4
Pene disc. Dimensiuni de pene si sectiuni de canale
(extras din STAS 1012-77)
|
Diametrul
arborelui, d
|
Dimensiunile
penei, [mm]
|
Dimensiunile
canalului de pana, [mm]
|
Masa
kg/103
buc.
|
|
Pentru pene
ca elemente de transmitere a momente-lor de torsiune
|
Pentru pene
ca elemente de fixare a pozitiei
|
b
|
h
|
D
|
Latimea, b
|
Adancimea
|
D0+0,5
|
R
|
|
Nominal
|
Nominal
|
Nominal
|
Nominal
|
Arbore, t1
|
Butuc, t2
|
|
Nominal
|
Abateri
limita
|
Nominal
|
Abateri
limita
|
|
Peste 12
pana la 14
|
Peste 18
pana la 20
|
4
|
6,5
|
16
|
4
|
5
|
+0,2
0
|
1.8
|
+0,1
0
|
16
|
0,25.
0,16
|
2,40
|
|
Peste 14
pana la 16
|
Peste 20
pana la 22
|
4
|
7,5
|
19
|
6
|
1.8
|
19
|
3,27
|
|
Peste 16
pana la 18
|
Peste 22
pana la 25
|
5
|
6,5
|
16
|
5
|
4,5
|
2.3
|
16
|
3,01
|
|
Peste 18
pana la 20
|
Peste 25
pana la 28
|
5
|
7,5
|
19
|
5,5
|
2.3
|
19
|
4,90
|
|
Peste 20
pana la 22
|
Peste 28
pana la 32
|
5
|
9
|
22
|
7
|
+0,3
0
|
2.3
|
22
|
5,30
|
|
Peste 22
pana la 25
|
Peste 32
pana la 36
|
6
|
9
|
25
|
6
|
6,5
|
2.8
|
22
|
6,80
|
|
Peste 25
pana la 28
|
Peste 36
pana la 40
|
6
|
10
|
25
|
7
|
3.3
|
+0,2
0
|
25
|
8,40
|
|
Peste 28
pana la 32
|
Peste 40
|
8
|
11
|
28
|
8
|
8
|
3.3
|
28
|
14,0
|
|
Peste 32
pana la 38
|
|
10
|
13
|
32
|
10
|
10
|
3.3
|
32
|
0,40.
0,25
|
21,0
|
2. Verificarea penei alese la forfecare:
|
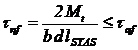
|
(17)
|
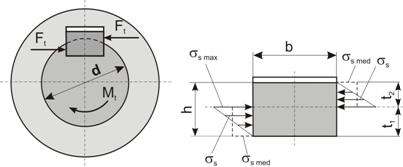
Fig. 8 Elemente de calcul
pentru pene paralele
Tensiunea admisibile de strivire, pentru materiale cu srt = (380.450) MPa pentru
arbore (otel) si srt = (200.250) MPa
pentru butuc (fonta cenusie) se pot
adopta astfel:
sas = (100.150) Mpa, pentru solicitari constante;
sas = (100.150) Mpa, pentru solicitari pulsatorii;
sas = (100.150) Mpa, pentru solicitari alternante si cu socuri;
sas = (100.150) Mpa, pentru imbinari mobile.
Tensiunile admisibile de
mai sus se pot determina aproximativ folosind si relatia:
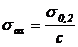 ,
,
in care: c - coeficient de siguranta cu valorile urmatoare:
c = 2.3, pentru sarcini statice, asamblari fixe;
c = 3.4, pentru sarcini dinamice, asamblari fixe;
c = 4.5, pentru sarcini dinamice, asamblari mobile;
taf = (0,2.0,3) s0,2 (pentru materialul penei).
2.4. Asamblari cu arbori profilati
La aceste tipuri de asamblari,
arborele si butucul au profile conjugate care nu fac posibila rotirea relativa
a arborelui fata de butuc, asigurand astfel transmiterea momentului de
torsiune, si functie de ajustajul butuc-arbore, si deplasari axiale. Dupa forma,
aceste asamblari pot fi: asamblari cu arbori canelati (caneluri) si asamblari
cu arbori poligonali.
1. Asamblari cu arbori canelati. La asamblarile canelate, atat arborii cat si
butucii au prevatute la periferia zonei imbinate proieminente si canale care se
imbina reciproc (profile conjugate). Ca mod de functionare si transmitere a
momentului de torsiune, canelurile pot fi asimilate cu o succesiune de pene
paralele longitudinale, avand avantajul unei capacitati portante mult sporite.
Asamblari cu arbori canelati se
utilizeaza la pentru transiterea de sarcini mari, cu asigurarea coaxialitatii
elementelor si in conditii de gabarite restranse (cutii de viteze, roti cu
deplasare axiala etc). Criteriul principal de alegere intre o asamblare cu pana
si una cu caneluri este unul tehnologic (costul relativ ridicat al prelucrarii
canelurii).
Clasificarea asamblarilor cu arbori
canelati se face dupa mai multe criterii:
1.
dupa
forma canelurilor
cu profil
dreptunghiular (tab. 5) serie usoara (fig. 9,a), STAS 1768-86, serie mijlocie
(fig. 9,b), STAS 1769-86, serie grea (fig. 9,c), STAS 1770-86);
cu profil triunghiular (fig. x.9,e) STAS 7346-83, cu profil in evolventa (fig. 9,f) STAS 6858-85'
cu profil dreptunghiular pentru masini unelte,
STAS 2670-78;
2. dupa modul in care se
realizeaza centrarea canelurilor
butucului pe cele ale arborelui:
interioara (pe
diametrul interior al canelurii arborelui, fig. 10,a);
exterioara (pe
diametrul exterior al canelurii arborelui, fig. 10,b);
laterala (pe
flancurile canelurilor, fig. 10,c);
3. dupa tipul asamblarii
fixa;
mobila (cu
posibilitati de deplasare axiala).
Canelurile dreptunghiulare sunt, din punct de vedere tehnologic, cel mai
simplu de executat (avand flancurile paralele cu planul median al acesteia),
motiv pentru care sunt cele mai utilizate. Centrarea se face in cele trei
moduri posibile (la diametre nominale mici se recomanda centrarea interioara,
la diametre mari, centrarea pe flancuri).
Canelurile triunghiulare, cu o buna rezistenta la oboseala de incovoiere,
sunt recomamdate pentru imbinari fixe ce transmit momente mari, cu socuri.
Centrarea se realizeaza pe flancuri. Avand inaltimea mica, permit un mare numar
de caneluri realizand o pozitionare buna a pieselor (imbinari de manivele,
fusuri, brate etc).
Canelurile in evolventa au o rezistenta sporita la oboseala, cu centrare
pe flancuri (recomandata pentru transmiterea momentelor cu schimbari dese de
sens si socuri) se utilizeaza in constructia de autovehicule (cutii de viteze,
mecanisme precise).
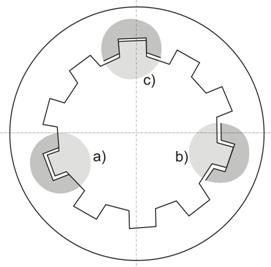
Fig. 10.
Posibilitati de centrare a canelurilor butucului cu cele ale arborelui:
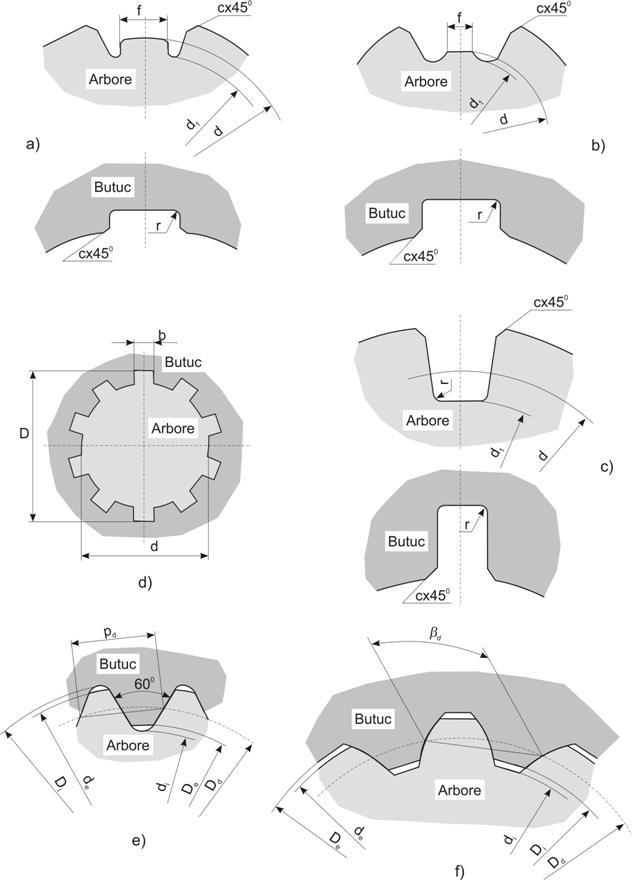
Fig. 9. Profiluri de caneluri:
a)-caneluri
dreptunghiulare (serie usoara); b)-caneluri dreptunghiulare (serie mijlocie);
c)-caneluri dreptunghiulare (serie grea); e)-caneluri
triunghiulare; f)-caneluri in evolventa
Elemente de calcul. In cazul asamblarilor cu caneluri (fig. 11)
transmiterea momentelor de torsiune se face prin contactul lateral al flancurilor,
deci solicitarea de
contact
este predominanta (solicitarile de incovoiere si forfecare a canelurilor sunt
neesentiale. Initial, se determina din fie din conditia de rezistenta la
incovoiere sau rasucire (sau ambele), fie constructiv, diametrul arborelui
(butucului) in zona imbinarii. Apoi se adopta tipul de canelura. Lungimea
canelurii (similar ca la penele paralele) rezulta din conditia de rezistenta la
contact (strivire):
Tabelul 5
Arbori si butuci canelati cu profil
dreptundghular. Dimensiuni, [mm]
|
d
|
Seria usoara
STAS 1768 86
|
Seria
mijlocie
STAS 1769 86
|
Seria grea
STAS 1770 86
|
|
D
|
b
|
z
|
Centrarea
|
D
|
b
|
z
|
Centrarea
|
D
|
b
|
z
|
Centrarea
|
|
11
13
16
18
21
23
26
28
32
36
42
46
52
56
62
72
82
92
102
112
|
26
30
32
36
40
46
50
58
62
68
78
88
98
108
120
|
6
6
7
6
7
8
9
10
10
12
12
12
14
16
18
|
|
|
14
16
20
22
25
28
32
34
38
42
48
54
60
65
72
82
92
102
112
125
|
3
3.5
4
5
5
6
6
7
6
7
8
9
10
10
12
12
12
14
16
18
|
6
|
Interioara
|
20
23
26
29
32
35
40
45
52
56
60
65
72
82
92
102
115
125
|
2.5
3
3
4
4
4
5
5
6
7
5
5
6
7
6
7
8
9
|
10
|
Interioara
sau pe flancuri
|
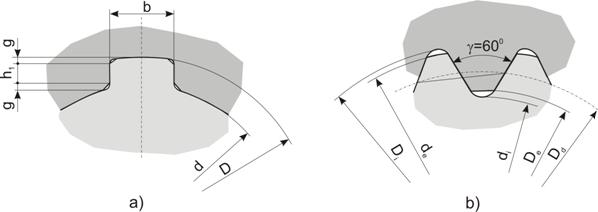
Fig. 11. Elemente de calcul pentru canelurile:
a)- triunghiulare; b)- caneluri in evolventa
|
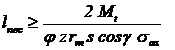
|
(18)
|
in care: j - coeficient de neuniformitate a repartitiei
sarcinii pe caneluri, datorita impreciziei de prelucrare: j = 0,75,
pentru caneluri dreptunghiulare si evolventice;
j = 0,50,
pentru caneluri triunghiulare;
z - numarul total de caneluri;
rm - raza medie: 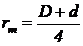 , pentru caneluri dreptunghiulare;
, pentru caneluri dreptunghiulare;
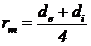 , pentru caneluri triunghiulare;
, pentru caneluri triunghiulare;
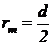 , pentru caneluri
evolventice.
, pentru caneluri
evolventice.
s - inaltimea de contact (s = h1):
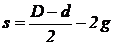 , pentru caneluri
dreptunghiulare;
, pentru caneluri
dreptunghiulare;
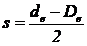 , pentru caneluri triunghiulare;
, pentru caneluri triunghiulare;
g - unghiul flancului, [grd]: g = 00, pentru caneluri dreptunghiulare;
g = 600, pentru unele caneluri triunghiulare;
sas
- tensiunea admisibila de contact: 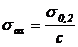 ,
,
in care: c - coeficient de siguranta cu
valorile urmatoare:
c = 2.3, pentru sarcini statice, asamblari fixe;
c = 3.4, pentru sarcini dinamice, asamblari fixe;
c = 4.5, pentru sarcini dinamice, asamblari mobile;
Pe aceasta baza, in STAS
1767-67 se da calcul complet pentru canelurile dreptunghiulare.
Recomandari
constructive. Fixarea, respectiv
posibilitatea de deplasare a butucului pe arbore se stabilesc functie de destinatie si de
ajustaj. In tab. 6 se dau unele indicatii
constructive pentru caneluri dreptunghiulare. In
privinta ajustajelor se recomanda utilizarea celor indicate in STAS 6565-79
(caneluri dreptunghiulare) si in STAS 7338-65 (caneluri in evolventa).
2.
Asamblari cu arbori poligonali. La aceste tipuri de asamblari, arborele are
in sectiune transversala, un contur poligonal (triunghiular, patrat si mai rar
hexagonal), adesea rotunjit, suprafetele de contact putand fi drepte sau curbe
(fig. 12). De-a-lungul asamblarii sectiunea poate fi constanta sau variabila
(conica). Printre avantajele acestor tipuri de imbinari fata de imbinarile cu
penese pot mentiona: evitarea canalelor, a muchiilor ascutite si a schimbarilor
bruste de sectiune, deci o reducere a concentrarilor de tensiuni si o mai buna
centrare a pieselor asamblate. Ca dezavantaje se pot enumera: costul ridicat de
fabricare (necesita utilaje si dispozitive speciale de executie si un grad mai mare de precizie), nu este posibila
deplasarea axiala a butucului sub sarcina.
Tabelul 6
Asamblari cu caneluri dreptundghulare.
Recomandari constructive
|
Seria
|
Domeniul de
utilizare
|
Lungimea L
recomandata pentru butuc
|
|
Momentul transmis
comparativ cu cel transmis de arborele cu diametrul, d
|
Tipul
asamblarii
|
|
Usoara STAS
1768 68
|
Inferior
|
Fixa
|
L = 1,5 d
|
|
Mijlocie
STAS 1769 68
|
Egal
|
Fixa sau
mobila, cu deplasarea axiala a butucului fara sarcina
|
L = (1,5 .
2,5) d
|
|
Grea STAS
1770 68
|
Egal
|
Mobila, cu
deplasare axiala a butucului sub sarcina
|
L = (1,5 .
2,5) d
|
Cele
mai folosite asamblari cu arbori poligonali sunt asamblarile cu profil
triunghiular utilizate la transmiterea sarcilnilor mari in imbinari fixe (mai
rar in imbinari mobile). Asamblarile cu profil p[atrat sau hexagonal sunt
folosite la transmiterea sarcinilor mici (de regula la fixarea parghiilor pe
arbori).
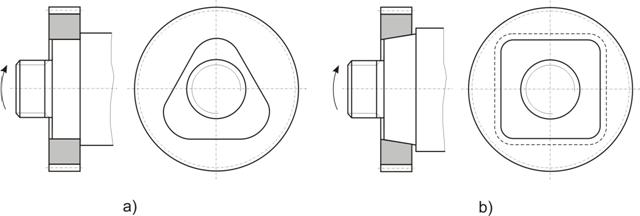
Fig. 12.
Asamblari cu arbori poligonali:
a)- cu sectiune constanta triunghiulara si ;
b)- cu sectiune variabila patrata
Calculul
acestor tipuri de imbinari este mai complex datorita starii de tensiune reale
in elementele asamblarii si a formei sectiunii imbinarii. Pentru simplificare
se considera ca tensiunea de contact este predominanta. In [OM-GAF] este prezentat un calcul de verificare la
solicitarea de contact pentru o imbinare cu profilul triunghiular, patrat,
hexagonal si cilindru tesit.
3. Asamblari cilindrice prin
strangere
Asamblarile cilindrice prin strangere
sunt asamblari demontabile care functioneaza pe baza fortelor de frecare care
apar intre butuc si arebore ca efect al actiunii normale pe suprafetele de
contact (cilindrice). Marimea solicitarilor transmise prin aceste tipuri de
asamblari (momente de torsiune, forte axiale) depinde in mod direct de valoarea
coeficientului de frecare m, care la randul sau este influientat de o serie de factori:
materialele cuplei de frecare, macro si microgeometria suprafetelor de contact,
existenta si
natura
lubrifiantului, prezenta oxizilor (tab. 7) etc. Daca se tine seama si de natura
solicitarii, pentru micsorarea gradului de incertitudine, se utilizeaza in
calcule coeficienti de siguranta, c adecvati determinati experimental.
Astfel: c = 1,2.1,5 pentru solicitari
normale; c = 2.4 pentru solicitari
dinamice cu soc.
Realizarea fortei normale necesare
functionarii unei asamblari prin strangere se face in doua moduri:
prin intermediul
unor elemente ca cleme, bucse, inele, saibe etc;
prin strangere
proprie;
combinat (de
exemplu asamblarea conica tensionata axial).
3.1 Asamblari cu cleme
La asamblarile cu cleme forta normale
(radiala) necesara transmiterii momentelor de torsiune, Mt
sau a fortelor axiale, FA se efectueaza cu ajutorul
suruburilor de strangere. In cazul transmiterii unor solicitari mici se poate utiliza un singur surub de strangere, dar
Tabelul 7
Valorile coeficientului de frecare m
|
Cuplul de materiale
|
Starea suprafetelor in contact
|
Calittaea suprafetelor in contact
|
m
|
|
Otel pe otel
|
Uscata fara oxizi
|
Arbore rectificat butuc alezat
Arbore rectificat fin butuc rectificat
|
0.1 . 0.3
0.25 . 0.4
|
|
Bine unsa
|
Arbore rectificat butuc alezat
Arbore rectificat fin butuc rectificat
|
0.07 .. 0.16
0.05 . 0.13
|
|
Otel pe fonta sau fonta pe fonta
|
Uscata fara oxizi
|
Arbore rectificat butuc alezat
Arbore rectificat fin butuc rectificat
|
0.15 . 0.25
0.17 . 0.33
|
|
Bine unsa
|
Arbore rectificat butuc alezat
Arbore rectificat fin butuc rectificat
|
0.06 . 0.13
0.02 . 0.1
|
|
Otel pe bronz
|
Uscata fara oxizi
Bine unsa
|
Arbore rectificat butuc alezat
|
0.13 . 0.25
0.02 . 0.1
|
|
Otel pe aliaj de aluminiu
|
Uscata fara oxizi
|
Arbore rectificat butuc alezat
|
0.03 . 0.08
|
|
Otel pe materiale plastice
|
Uscata fara oxizi
|
Arbore rectificat butuc alezat
|
0.33
|
pentru asigurarea
uniformitatii necesare presarii suprafetelor in contact pe toata lungimea
asamblarii numarul de suruburi se alege constructiv, urmand a se verifica
presiunea de contact si suruburile la intindere.
Utilizand notatiile din fig. 13 se
pot stabili cateva relatii de calcul generale pentru asamblarile de uz general:
suprafata de
frecare: 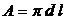
lungimea
necesara a butucului:
|
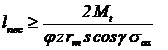
|
(19)
|
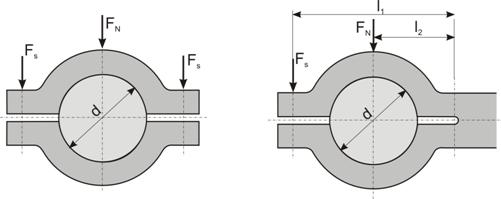
Fig. 13. Model de calcul pentru asamblari cu cleme de uz
general
unde: c - coeficientul de siguranta;
pa - presiunea
admisibila pentru materialul cel mai slab aflat in contact.
forta necesara
(normala) a se realiza cu ajutorul suruburilor:
|
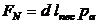
|
(20)
|
forta necesara
repartizata pe toate suruburile (functie de solutia constructiva):
|
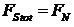 sau sau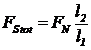
|
(21)
|
forta necesara
repartizata pe un surub (z-numarul de suruburi):
|
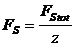
|
(22)
|
Observatie: Forta FS
se majoreaza cu 30% pentru a se tine seama de solicitarea de
torsiune ce apare la strangerea cu cheia.
In cazul asamblarilor precise este
necesar un calcul mai exact (fig. 14,a). Variatia reala a presiunii pe
suprafata de contact este prezentata in fig. 14,c diferita de cea prezentata in
fig. 14,a si este determinata de macro si microgeometria suprafetelor in
contact precum si de rigiditatea la incovoiere a butucului (cu cat rigiditatea
butucului este mai mica cu atat contactul este mai complet si presiunea mai
uniforma). Pentru cazul clasic al unui butuc elastic la incovoiere (fig. 14.a,
b) este necesar sa se faca distinctie
intre presiunea p pe suprafata proiectata ld si presiunea medie pm
pe suprafata de contact (fortele FN si N fiind in echilibru):
|
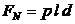
|
(23)
|
|
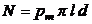
|
(24)
|
Presiunea medie pm
este media aritmetica a repartitiei efective a presiunilor pe conturul
arborelui este:
|
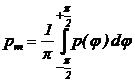
|
(25)
|
Presiunea p pe suprafata proiectata rezulta din componentele verticale ale
presiunii efective p(j
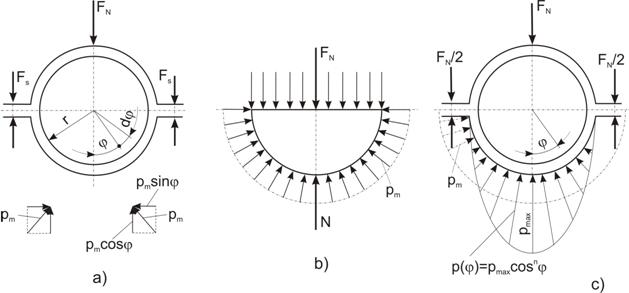
Fig. 14.
Model de calcul precis pentru asamblari prin presare:
a)-model de
calcul mai exact; b)-distributie simplificata a presiunilor; c)- distributie
reala a presinilor
|
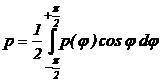
|
(26)
|
unde: p(j -
presiunea efectiva de contact.
Pentru determinarea repartitiei
presiunii efective de contact, p(j in [OM-Gaf] se utilizeaza o aproximatie de tipul:
|
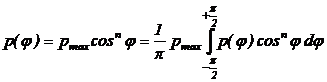
|
(27)
|
Pentru diferita valori ale
exponentului n = 0, 1, 2, 3, . se pot regasi cateva cazuri particulare [OM-Gaf].
Deoarece in practica, datorita
cunoasterii insuficiente a rigiditatii butucului, evaluarea exacta a presiunii pmax
este dificila, pentru determinarea momentul de torsiune capabil se face aproximatia p(j) = const.
In acest caz momentul de torsiune capabil este:
|
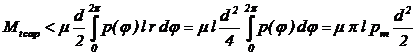
|
(28)
|
sau in
ideea utilizarii unui coeficient de siguranta, c:
|
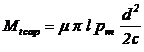
|
(29)
|
Pentru asigurarea unei
repartitii cat mai uniforme a presiunii pe suprafata de contact sunt necesare
printre altele:
alegerea unui
ajustaj corespunzator a clemei pe arbore; se recomanda ajustajele: H7/h6
sau K7/h6, pentru diametre de pana la 60 mm, H7/m6 sau M7/h6,
pentru diametre peste 60 mm;
o calitate
buna a suprafetelor in contact; se recomanda Ra = 3,2 pentru
alezaje si Ra = 1,6 pentru arbori;
o montare
ingrijita;
pentru clemele
cu strangere radiala se recomanda ca diametrul exterior al clemei sa fie: D
= (1,8.2) d.
Principalele avantaje ale
asamblarilor cu cleme sunt: simplitatea constructiva, realizarea unor strangeri
reglabile si demontarea usoara.
Domeniul de aplicare al
acestui tip de asamblare este foarte divers: solidarizarea pe arbori sau osii,
pe coloane sau tije, pe ghidaje fixe sau mobile a unor organe de masini fixe,
rotative sau oscilante care de multe ori fac corp comun cu clema insasi. Ca
exemple de utilizare se pot aminti: fixarea pe ghidaje a sistemelor de masura
si control pentru aparatele de laborator, pozitionarea mecanismelor masinilor
unelte pe coloane sau ghidaje orizontale, pozitionarea limitatorilor etc.
3.2 Asamblari cilindrice
prin presare
3.2.1 Notiuni genarale
La aceste tipuri de asamblari
demontabile fixarea butucului rotilor pe arbore in vederea transmiterii
momentelor de rasucire ca si a fortelor axiale fara patinare, se obtine prin
realizarea unui ajustaj cu strangere intre butuc si arbore (de regula in sistem
alezaj unitar). Aceasta inseamna ca inainte de asamblare diametrul arborelui
trebuie sa fie mai mic decat cel al alezajului butucului.
Dupa asamblare are loc o crestere a
alezajului cu valoarea Db si o micsorare a
diametrului arborelui cu Da, obtinundu-se in final
un diametru comun d (fig. 15,a). Se realizeaza o strangere aparenta de valoare:
|
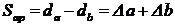
|
(30)
|
Ca efect direct al strangerii, pe
suprafatele de contact varfurile rugozitatilor arborelui si butucului se reduc
cu o valoare totala DS astfel incat asigurarea
presiunii de contact necesare strangerii se datoreaza numai strangerii
efective:
|
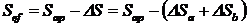
|
(31)
|
Considerand ca netezirea
varfurile rugozitatilor se produce pana la o valoare de 0,6Rmax, rezulta [OM-Gaf]:
|
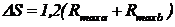
|
(32)
|
unde: Rmax a,
Rmax b - inaltimea asperitatilor de suprafata ale arborelui,
respectiv ale butucului, tab.
Tabelul 8
Inaltimea
microneregularitatilor de suprafata, Rmax
|
Felul
prelucrarii
|
Rmax mm]
|
Felul
prelucrarii
|
Rmax mm]
|
|
Lustruire
Lepuire fina
Lepuire
Honuire
Rectificare
foarte fina
Rectificare
fina
Rectificare
Razuire 3.5
puncte/cm2
Razuire 1.3
puncte/cm2
Brosare
|
0.10 . 0.40
0.16 . 1.0
0.60 . 4.0
0.10 . 1.0
0.10 . 1.0
1.0 . 4.0
4.0 . 10.0
2.5. 10.0
10.0. 40.0
2.5 . 10.0
|
Alezare fina
Alezare
Strunjire
fina cu diamant
Strunjire
fina cu metal dur
Netezire
prin strunjire
Strunjire
grosolana
Frezare fina
Netezire
prin frezare
Netezire
prin rabotare
Rabotare
grosolana
|
1.0 . 4.0
4.0 . 10.0
1.0 . 2.5
2.5 . 10.0
10.0 . 40.0
40.0 . 100.0
4.0 . 10.0
10.0 . 40.0
10.0 . 40.0
40.0 . 100.0
|
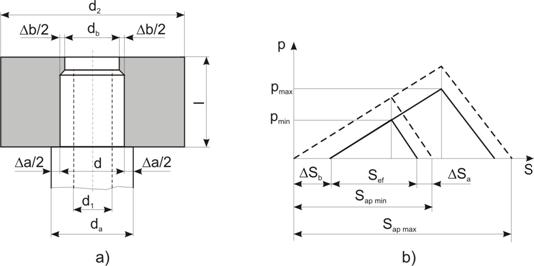
Fig. 15 Elementele generale ale
unei asamblari cilindrice prin presare:
a)-dimensiuni; b)-diagrama de tensionare
Datorita presiunii efectuate
de alezaj asupra arborelui, pe suprafata de contact ia nastere o presiune p
a carei variatie cu strangerea este data in fig. 15,b. (diagrama de
strangere).
Pentru desfacerea unei astfel
de asamblari trebuiesc invinse fortele de frecare ce apar la suprafata de
contact dintre alazaj si arbore. Pentru determinarea momentului de torsiune
capabil se pleaca se la ipoteza mentinerii in domeniul elastic al
solicitarii si deformatiei in zona de contact. Daca se noteaza cu l si
d lungimea, respectiv diametrul imbinarii prin strangere si cu p presiunea
uniform distribuita de pe suprafata de contact (fig. 16), atunci forta totala
de frecare a asamblarii este:
|
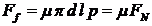
|
(33)
|
Daca se defineste un
coeficient de siguranta al asamblarii, c > 1, atunuci momentul de
torsiune capabil al intregii abamblari cu stangere este:
|
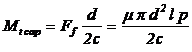
|
(34)
|
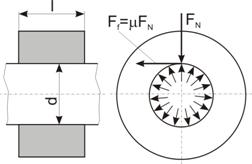
 Fig. 16. Model de calcul genaral al unei asamblari cilindrice
prin presare:
Fig. 16. Model de calcul genaral al unei asamblari cilindrice
prin presare:
Principalele avantaje
ale acestui tip de asamblare fata de
cele clasice sunt :
posibilitatea
transmiterii unor momente de torsiune si forte axiale mari si foarte
mari in regim de solicitare statica si
dinamica (solicitari alternante sau cu socuri);
asigurarea
unor centrari foarte precise;
gabarit si
pret de cost redus;
economie de
material si manopera.
Ca dezavantaje
se pot enumera:
tehnologia
specifica utilizata la montare-demonatre;
posibilitatea
deteriorarii suprafetelor de contact in timpul demontarii;
necesitatea
selectarii prealabile (imperechierii) a pieselor conjugate in scopul reducerii
domeniului de variatie a strangerii la acelasi tip de ajustaj si la acelasi
diametru nominal.
Asamblarile
prin presare sunt utilizate in:
realizarea
unor asamblari compuse din doua organe de masini cu functiuni diferite
(rulmenti pe arbori, roti pe arbori, bucse de lagare de frictiune in carcase
etc)
constituirea
din parti componente a unui organ de masina (coroana dintata pe corpul rotii,
bandajul pe discul rotii de vagon, realizarea unui arbore cotit din fusuri si
manetoane fabricate separat).
Tehnologiile
de realizare a asamblarii prin presare sunt:
a. Asamblari prin
deplasarea radiala a suprafetelor de contact realizata prin contractia butucului incalzit in prealabil si dilatatia
arborelui subracit in prealabil. Incalzirea butucului se efectueaza: pe placa
incalzitoare (pana la +100 0C), in baie de ulei (pana la +370
0C) si in cuptor cu gaze, electric sau cu inductie (pana la 700
0C). Deoarece la incalzirire peste 300 0C la
piesele din otel apare un strat superficial de arsura (tunder), lucru nepermis
in cazul asamblarilor demontabile, este necesar ca la aceste temperaturi
incalzirea sa se faca in cuptoare cu atmosfera reducatoare sau vid. Pentru
subracirea arborilor se foloseste zapada carbonica (pana la -70 0C)
sau aer lichid (pana la -190 0C).
b. Asamblari prin presare
longitudinala ce se executa la temperatura ambianta si care
constau in introducerea butucului pe arbore (sau invers), prin presare,
utiluzand pentru aceasta prese (hidraulice sau cu surub) cu viteze mici (cca 2
mm/s). In cazul diametrelor nominale mari (elice de nave, bucse de
frictiune in carcasele morilor de ciment) se introduce, prin canale special
practicate, ulei la presiuni mari (200
bar) intre cele doua piese de asamblat. Ca urmare a presiunii mari, se
elimina deferentele de dimensiuni dintre arbore si butuc prin deformatii
elastice facand posibila montarea (demontarea). Pentru demontarea asamblarii
realizate prin incalzire (racire) se incalzeste (raceste) butucul (arborele).
3.2.2 Elemente de calcul
1. Asamblare arbore
tubular-butuc gros In cazul general al strangerii intre arbore si
butuc, la nivelul suprafetei de contact, apare o stare triaxiala de tensiuni: st sr si sz.
Pentru simplificare se introduce ipoteza starii plane de tensiuni (sz
= 0), considerandu-se lungimea
butucului infinita. Distributia si valoarea tensiunilor st
si sr , cunoscuta din teoria elasticitatii (relatiile
lui Lame), sunt date in fig. 17, respectiv in tab. 9
Din aceste
relatii se vede ca marimile tensiunilor depind de valoarea presiunii p
deci implicit de valoarea strangerii efective, Sef . Tinand
seama de deformatiile (specifice) elastice ale arborelui si butucului si
utilizand legea lui Hooke pentru starea plana de tensiuni se poate determina
strangerea efectiva [OM-Gaf]:
|
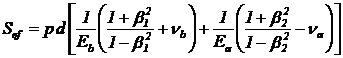
|
(35)
|
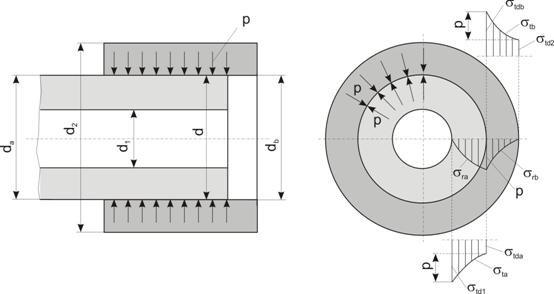
Fig. 17. Distributia tensiunilor la o asamblare cilindrice prin
presare in ipoteza starii plana de tensiuni
unde: υa,
υb - constantele lui Poisson pentru materialul
arborelui, respectiv al butucului (pentru otel, υ = 10/3, iar pentru fonta υ
4
Ea, Eb - modulele de elesticitate longitudinale pentru
materialul arborelui, respectiv al butucului.
Pentru cazul in care arborele este
plin (b2 = 0) iar materialele arborelui si butucului sunt
de aceiasi natura (Ea = Eb
= E) relatia (35) devine:
|
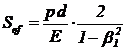
|
(36)
|
Tabelul 9
Relatiile lui Lame pentru o asamblare cilindrice
prin presare in ipoteza starii plana de tensiuni
|
Tensiunea
tangentiala
|
Tensiunea radiala
|
|
Butuc
|
Arbore
|
Butuc
|
Arbore
|
|
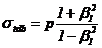
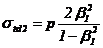
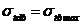
|
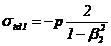
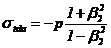
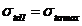
|
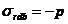
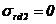
|
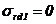
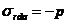
|
|
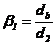 
|
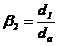 
|
|
Pentru transmiterea fara
patinare a momentului de torsiune a
fortei axiale sau a ambelor simultan (fig. 18), este necesar ca presiunea
dintre arbore si alezaj sa aiba o valoare minima, pmin. Este evident faptul ca valoarea pmin
pmax
= pas (presiunea
admisibila a materialului cu caracteristicile de rezistenta cele mai scazute).
In tab. 10 sunt indicate relatii de determinare a presiunii minime necesare la
asamblarile prin presare.
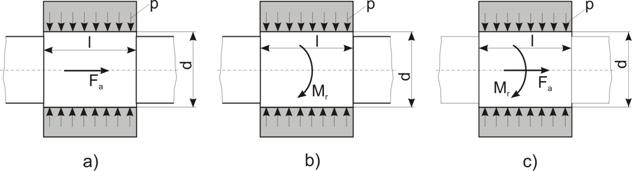
Fig. 1 Solicitari transmise prin asamblarile prin
presare
Pentru calculul de
verificare, in cazul cel mai frecvent al asamblarilor cu strangere prin
presare elastice, folosind teoriile de rezistenta, se pot determina
tensiunile echivalente pentru diametrul interior al butucului, db
si diametrul interior al arborelui tubular, d1:
Tabelul 10
Relatii de calcul pentru presiunea minima necesare la asamblarile prin
presare
|
Solicitarea
(conf. fig. 6)
|
Conditia
de preluare prin frecare
|
Presiunea
minima necesara
|
Forta axiala
|
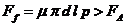
|
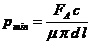
|
Moment de torsiune
|
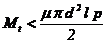
|
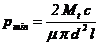
|
|
Forta axiala
Moment de torsiune
|
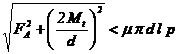
|
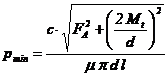
|
pentru butuc:
|
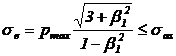
|
(37)
|
pentru arbore:
|
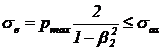
|
(38)
|
in care: sas
- tensiunea admisibila la strivire al materialului.
Tensiunea admisibila la
strivire are pentru un calcul aproximativ valorile:
pentru
materialele tenace :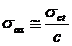 ,
,
unde: sct
- limita de curgere la tractiune;
c -
coeficientul de siguranta (c = 1,1.1,3)
pentru
materialele fragile : 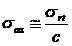 ,
,
unde: srt
- rezistenta de rupere la tractiune;
c = 1,1.1,3.
Daca se inlocuieste in
relatia (35) valoarea lui pmin
si valoarea cea mai mica a lui pmax
(pas a materialului cu
caracteristicile de rezistenta cele mai scazute), se obtin strangerile efective
minima si maxima Sef min si Sef max, iar
din relatia (31) strangerile aparente minima si maxima Sap min
si Sap max. Strangerile standard, Ss
trebuie sa indeplineasca se conditiile:

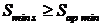 ;
; 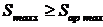
Valorile Smin s
si Smax s servesc pentru alegerea ajustajului, care trebuie
sa faca parte din seria ajustajelor preferentiale, conform STAS 8100/4-8
Pentru asamblarea prin
presare longitudinala (axiala) forta axiala necesara rezulta din tab. 10, in care
se inlocuieste p pmax
Pentru asamblarea prin
presare prin deplasare radiala a suprafetei de cotact, diferenta de temperatura
necesara pentru intruducerea libera a arborelui in butuc este:
|
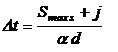 , [0C] , [0C]
|
(39)
|
unde: Smax
s - diferenta maxima dintre diametrul arborelui si al alezajului
butucului dupa alegerea ajustajului, [mm];
j - jocul de montaj, [mm]; se recomanda: j (d/1000);
a - coeficientul de
dilatare termica al materialului arborelui sau butucului, [1/0C].
Calculul indicat mai sus nu
este suficient pentru cazul functionarii la turatii ridicate ale ansamblului
butuc-arbore sau in cazul cand arborele sau butucul functioneaza la temperaturi
diferite.
Daca ansamblul se roteste la
turatii ridicate, datorita actiunii fortei centrifuge diametrul alezajului
butucului se largeste cu o valoare mai mare decat diametrul arboirelui, astfel
ca presiunea de la suprafata de contact scade. De aceea la aceste imbinari
trebuiesc luate masuri pentru cresterea valorii pmin.
In cazul in care arborele si
butucul au coeficienti de dilatare termica diferiti sau in cazul in care
arborele si butucul, imbinati prin asamblare prin presare, functioneaza la
temperaturi diferite, este necesar sa se calculeze diferentele de dilatare a
butucului si arborelui la nivelul diametrului d si sa se tina seama de
sensul lor.
In afara de asamblarile cu strangere prin presare
elastice se mai utilizeaza asamblarile cu strangere prin presare
elasto-plastice, aplicabile materialelor tenace la care strangerile pot fi atat
de mari incat la nivelul diametrului nominal, d, in zona cea mai solicitata
limita de curgere este depasit si ca urmare se produc importante deformatii
plastice pe o zona limitata denumita raza de plasticitate. Odata cu
cresterea strangerii aceasta zona se poate extinde pana la diametrul exterior
al butucului, d2, producand o plasticizare completa.
Asamblarile cu strangere prin presare elasto-plastice fara atingerea
plasticizarii complete sunt foarte rationale din punct de vedere al utilizarii
resurselor de rezistenta ale materialelor tenace.
2. Asamblare arbore plin
- butuc subtire (bucsa). In cazul
in care grosimea butucului este mult mai mica decat raza arborelui se poate
admite ca deformatia radiala er
= 0 si tensiunea radiala sr
= 0, astfel ca, in coformitate cu
teoria invelisurilor subtiri, presiunea de pe suprafata de contact, p,
datorata strangerii aparente Sap, produce numai tensiuni de
intindere st in bucsa (butuc) cu repartitie constanta in
sectiune (fig. 19), a carei valoare este:
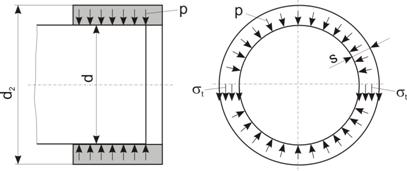
Fig. x.19. Model de calcul pentru arbore plin-butuc
subtire
|
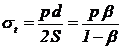 ; ; 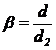
|
(40)
|
Strangerea efectiva este in
acest caz:
|
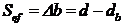
|
(41)
|
Actiunea presiunii p
determina cresterea diametrului bucsei. Strangerea efectiva rezulta:
|
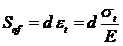
|
(42)
|
in care: et -
deformatia specifica diametrala, in sens tangential.
Inlocuind in relatia (35) valoarea
lui st din relatia (40) se obtine:
|
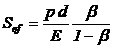
|
(43)
|
3.2.3 Metodica de calcul a
asamblarilor cilindrice prin presare
Pentru calculul unei
asamblari cilindrice prin presare este necesa de parcurgerea urmatoarelor
etape:
1.
Stabilirea
datelor initiale: d, da, db, d1, d2
si a coeficientului de siguranta, c.
2.
Stabilirea
caracteristicilor de rezistenta pentru materialele arborelui si butucului, sas
3.
Determinarea
presiunii minime de contact a asamblarii, pmin din conditia
transmiterii fara patinare a fortei axiale, FA, a momentului
de torsiune, Mt sau a
amandorora, cu relatiile date in tab. 10.
4.
Stabilirea
strangerilor efective minime necesare si maxime, Sef min prin inlocuirea in relatia (35) a valorii p
cu pmin.
5.
Stabilirea
strangerilor efective maxime, Sef max prin inlocuirea in
relatia (35) a valorii p cu pmax = sas
(tensiunea admisibila la strivire se ia cea corespunzatoare materialului cu
caracteristicile de rezistenta mai scazute), inclusiv calculul de verificare
pentru tensiunile echivalente la butuc si arbore cu relatiile (37, 38).
6. Se determina strangerile
aparente minime necesare si maxime, Sap min si Sap max utilizand pentru
aceasta relatia (31).
7.
Se adopta
ajustajul, care trebuie sa faca parte din seria ajustajelor preferentiale, conform
STAS 8104-6
1.Determinarea
fortei axiale, FA necesare pentru asamblarea prin presare longitudinala
utilizand relatia din tab. 10, in care se inlocuieste p pmax
2. Determinarea diferentei de
temperatura, Dt necesare asamblarii
prin deplasare radiala a suprafetelor de contact utilizand relatia (39).
3.3 Asamblari conice prin
presare
La asamblarile conice prin
presare forta radiala necesara pentru transmiterea momentului de torsiune fara
patinare, este realizata in doua moduri:
imbinari cu
autoblocare (prin strangere
proprie, fig. 20,a), la care semiunghiul conului din asamblare se gaseste fata
de unghiul de frecare, r, in relatia: 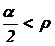 (tab.11);
(tab.11);
imbinari
fara autoblocare (prin strangere
cu ajutorul unei piulite, fig. 20), la care semiunghiul conului din asamblare
se gaseste fata de unghiul de frecare, r, in
relatia: 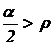 ;
;
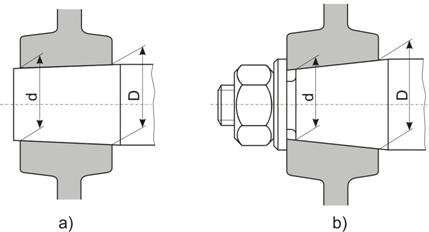
Fig. 20 Asamblari conice prin presare:
a)-prin
autoblocare; b)-prin strangere
Cu
notatiile din fig. 21,a, pentru un element din portiunea conica, in ipoteza
unei presiuni constante pe suprafata conica de contact, forta normala
elementara si forta normala, respectiv momentul de frecare elementar si
momentul de frecare sunt (cu dm = 0,5 (D + d), diametrul
mediu):
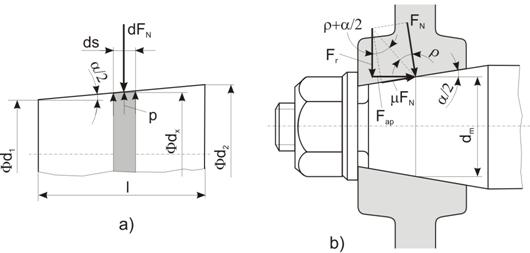
Fig. 21 Elemente de calcul pentru asamblari conice
prin presare:
a)-prin
autoblocare; b)-prin strangere
si notand
cu c coeficientul de siguranta momentul capabil al imbinarii este:
|
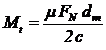
|
(46)
|
Presiunea minima (normala)
pe suprafata conica de contact este:
|
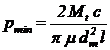
|
(47)
|
Forta axiala de presare
necesara pentru asigurarea presiunii minime pe suprafata de contact este:
|
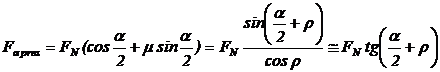 , ,
|
(48)
|
si cu
relatia (46) rezulta:
|
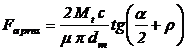
|
(49)
|
Forta
axiala pentru depresare este (se
schimba sensul fortei de frecare):
|
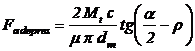
|
(50)
|
In analogie cu strangerea
cilindrica, strangerea aparenta este:
|
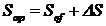 , ,
|
(51)
|
si se
realizeaza prin deplasarea axiala Dl
|
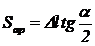
|
(52)
|
Pentru determinarea valorii medii
a strangerii efective minime, Sef min, este necesar:
se inlocuieste
suprafata conica cu o suprafata cilindrica medie, aftfel ca rapoartele b1
si b2 din relatia (35) devin (pentru cazul arborelui
tubular) 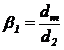 si
si 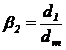 (d1
fiind diametrul interior al arborelui, iar d2, diametrul
exterior al butucului);
(d1
fiind diametrul interior al arborelui, iar d2, diametrul
exterior al butucului);
presiunea din
relatia (35) se inlocuieste cu componenta radiala a presiunii pmin:
|
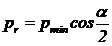
|
(53)
|
Avantajul asamblarii conice
prin presare fata de cea cilindrica consta in faptul ca se poate realiza o
asamblare prin presare la care cele doua componente (arborele si butucul) au
diametre diferite, la o cursa axiala relativ mica, prin deplasare axiala
reciproca. In plus aceasta asamblare mai are avantajul ca fortele de
presare-depresare sunt mici, exista posibilitatea de reglare a cursei, iar
cursele de presare-depresare sunt scurte.
Dezavantajele constau in
dificultatea efectuarii unui calcul exact al tensiunilor axiale, radiale si
tangentiale la ajustajele conice (deoarece forta de presare poate fi indicata
cu o precizie limitata) si in necesitatea asigurarii unei conicitati exacta a
arborelui si butucului.
Metodica de calcul pentru
asamblarile prin presare conice este urmatoarea:
1.
Calculul
presiunii minime la nivelul suprafetelor de contact, pmin din
conditia de transmitere fara patinare a momentului de torsiune, Mt,
utilizand relatia (47).
2.
Determinarea
fortei axiale de presare minime, Fa pres min cu relatia (49).
3.
Stabilirea
strangerii efective minime, Sef min din relatia (35)
inlocuind suprafata conica cu o suprafata cilindrica medie, de diametru dm
si pmin pr din relatia (53).
4.
Stabilirea
strangerii aparente minime, Sap min cu relatia (51).
5.
Determinarea
cursei de presare axiale minime, Dlmin cu relatia (52).
6.
Stabilirea
caracteristicilor de rezistenta ale materialului, sas
pentru materialele arborelui si ale butucului; se considera ca presiunea maxima
de presare, pmax = sas
(pentru materialul cel mai slab), si in plus se efectueaza verificari pentru
cele doua piese in contact cu relatiile (37) si (38).
7.
Se calculeaza
strangerea efective maxima, Sef max, similar ca la pc. 3.
8.
Se calculeaza
strangerea aparenta maxima, Sap max, similar ca la pc. 4.
9.
Se determina
cursei de presare axiale maxima, Dlmax, similar ca la pc. 5.
10. Se determina forta de presare axiala maxima, Fa
pres max utilizand o relatie similata cu (48):
|
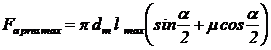
|
(54)
|
Pentru asigurarea unei presiuni cat mai uniforme a presiunii la
nivelul suprafetei de contact se recomanda urmatoarele:
abaterea de la
conicitate, in clasa 7-a de precizie;
rugozitatea
suprafetei alezajului, Ra = 1,6 mm, si
a alezajului, Ra = 0,87mm
campul de
toleranta pentru diametrul d al arborelui, h6.
3.4 Asamblari cu inele
tronconice
La aceste asamblari, forta
radiala (normala) necesara pentru transmiterea momentului de torsiune fara
patinare, este obtinuta prin deformatia radiala a unor inele tronconice,
ca urmare a actiunii unei forte de impingere axiale data de o piulita sau
suruburi de strangere. Inelele tronconice (fig. 22 si tab. 11) sunt doua inele
circulare inchise cu sectiuni tronconice asezate suprapus, inelul exterior fiind
cilindric la exterior si conic la interior, iar inelul interior este cilindric la interior si conic la exterior.
Conicitatea celor doua inele pe zona de contact este aceiasi.
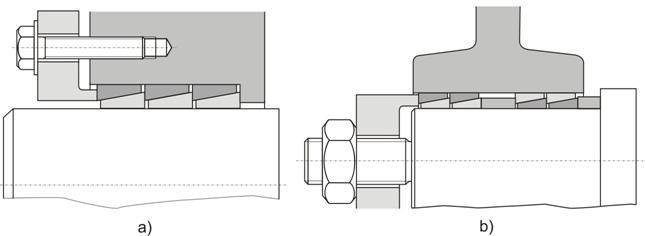
Fig. 22. Asamblari realizate cu inele tronconice la care
forta axiala este data de:
a)-strangere cu mai multe suruburi; b)-cu o singura
piulita
Ca urmare a fortei de
impingere axiale, Fa, in
inele vor aparea tensiuni de intindere (inelul exterior) si de compresiune
(inelul interior) care vor deforma cele doua inele corespunzator: inelul
exterior isi va mari diametrul exterior, iar inelul interior isi va micsora
diametrul interior. Aceste deformatii conduc la aparitia de presiuni pe
suprafetele de contact butuc-inel exterior-inel interior-arbore, a caror
valoare este functie de marimea fortei axiale de impingere. Cresterea acestei
forte conduce la deformarea inelelor in sensul aratat, pana la anularea
jocurilor de montaj, moment din care pe suprafetele de contact apar strangeri
fatorate fortelor de frecare ce actioneaza la nivelul acestor suprafete. Acest
lucru inseamna ca la o anumita valoare a fortei axiale se poate tramsmite
momentul de torsiune fara patinare. O pereche de inele tronconice pot
transmite, in functie de marime, momemte de torsiune relativ mici. Pemtru
transmiterea momentuler de torsiune de valori mari este necesara inserierea mai
multor perechi de inele. Fortele axiale preluate de la perechea de inele
precedente sunt transmise perechii urmatoare cu valori diminuate datorita
actiunii fortelor de frecare. De aceea numarul maxim de perechi de inele
tronconice este patru.
Avantajele acestui tip de
asamblare sunt in principal: posibilitatea unei montari-demontari relativ
usaore, asigurarea unei bune centrari a butucului fata de arbore, posibilitatea
patinarii inelelor fara pericol de deteriorare a suprafeleror active ale
arborelui, respectiv a alezajului butucului, in cazul aparitiei suprasarcinilor
de scurta durata, posibilitatea fabricarii inelelor in serii mari etc.
Ca dezaavantaje se pot
enumera cresterea gabaritului radial al asamblarii si necesitatea existentei
unui sistem de impingere axiala a inelelor.
Pentru realizarea unei
asamblari corecte se recomanda urmatoarele tolerante: m5, k5, m6, h7
(pentru arbore) si H7, H8 (pentru alezajul butucului).
Metodica de calcul a
asamblarii prin presare cu inele tronconice comporta parcurgerea urmatoarelor etape:
1.
Stabilirea
caracteristicilor de rezistenta ale materialului, sas
pentru materialele arborelui si ale butucului; se considera ca presiunea maxima
de presare, pmax = sas
(pentru materialul cel mai slab).
2.
Determinarea
fortei radiale (normale) maxime, FN max corespunzatoare
presiunii maxime, pmax.
3.
Calculul
momentului de torsiune capabil transmis de o singura pereche de inele
tronconice, Mt1.
4.
Stabilirea
numarului de perechi de inele tronconice necesare pentru tramsmiterea
momentului de torsiune total, Mt.
5.
Calculul
fortei axiale de impingere totale, FA necesara pentru
tramsmiterea momentului de torsiune total, Mt.
Tabelul 7.11
Dimensiuni de inele tronconice
recomandate, [mm]
|
d D
|
L
|
l
|
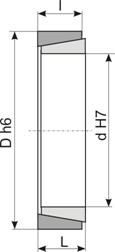
|
|
30 35
35 40
40 45
45 52
50 57
55 62
60 68
65 73
70 79
75 84
80 91
85 96
90 101
95 106
100 114
110 124
120 134
130 148
140 158
|
6.3
7
8
10
10
10
12
12
14
14
17
17
17
17
21
21
21
28
28
28
|
5.3
6
6.6
6
6
6
10.4
10.4
12.2
12.2
15
15
15
15
17
17
17
25.3
25.3
25.3
|
O varianta mai recenta a
asamblarii cu inele tronconice este cea cu inel circular inchis avand alezajul
cilindric la interior, iar la exterior conicitate dubla pe care se monteaza
doua flanse cu conicitati corespunzatoare la interior. Pentru realizarea
asamblarii cele doua flanse se strang (se apropie) cu ajutorul unor
suruburi,fig. 23.
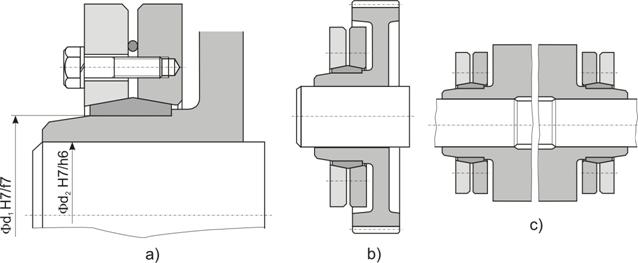
Fig. 23. Varianta de asamblare prin strangere realizata cu
inele cu dubla conicitate:
a)-elemente de
detaliu ale asamblarii; b,c)-utilizari ale acestui tip de asamblare.




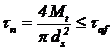
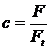
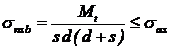
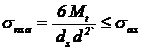

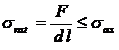
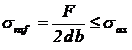
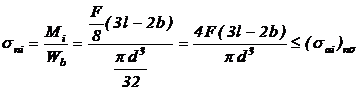
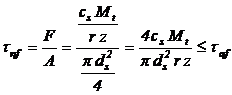


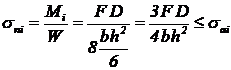

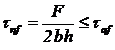
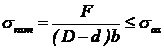
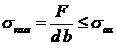


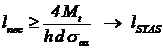

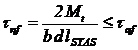




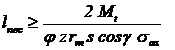

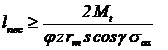

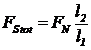
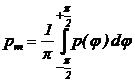

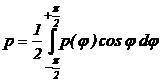
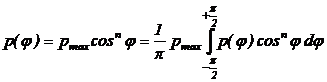
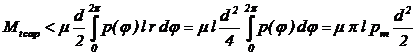
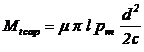

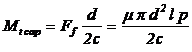

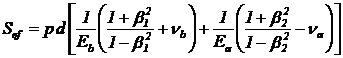

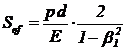

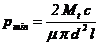
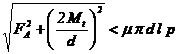
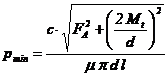
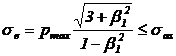
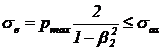
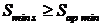 ;
; 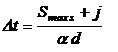 , [0C]
, [0C] 
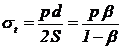 ;
; 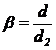


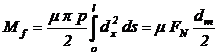 ,
, 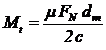
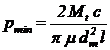
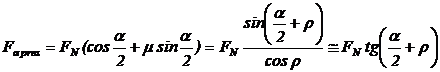 ,
,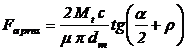
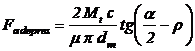
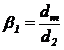 si
si 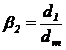 (d1
fiind diametrul interior al arborelui, iar d2, diametrul
exterior al butucului);
(d1
fiind diametrul interior al arborelui, iar d2, diametrul
exterior al butucului);