Teorema Hille - Yosida
Am vazut
ca generatorul infinetezimal al
unui 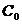 - semigrup este un
operator inchis si dens infinit.
- semigrup este un
operator inchis si dens infinit.
Problema. Dat un operator inchis si dens definit, genereaza
acesta un
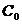 - semigrup?
- semigrup?
In general , raspunsul este negativ. Totusi
in anumite conditii suplimentare problema de mai sus are o solutie. Scopul
acesui paragraf este de a stabili o conditie necesara si
suficienta pentru ca un operator dens definit si inchis sa fie
generatorul unui
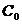 - semigrup.
- semigrup.
Teorema
I.4.1. Fie S =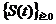 un
un 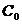 - semigrup pe spatiul Banach X, iar A generatorul
sau infinetezimal. Atunci exista M
- semigrup pe spatiul Banach X, iar A generatorul
sau infinetezimal. Atunci exista M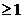 si
si 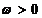 astfel incat
astfel incat
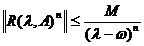 ,
, 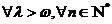 .
.
Demonstratie. Fie M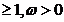 dati
din Teorema I.1.1. Atunci
dati
din Teorema I.1.1. Atunci 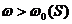 si din Teorema I.3.2.
rezulta ca pentru orice
si din Teorema I.3.2.
rezulta ca pentru orice 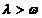 avem
avem
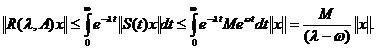
Ca
o consecinta a identitatii rezolvantei se obtine
imediat ca
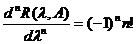
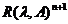 ,
,
deci
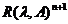 =(-1)
=(-1)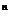
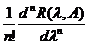 . (1.11)
. (1.11)
Din reprezentarea pentru aplicatia
rezolventa data din Teorema I.3.2 observam ca
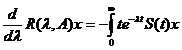 dt (1.12)
dt (1.12)
si inductiv rezulta
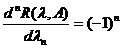
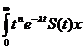 dt
dt
Din relatiile (1.11) si (1.12) deducem
ca
n! 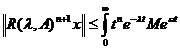 dt
dt 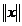 =
=
=M 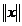
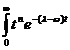 dt
dt 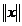 (1.13)
(1.13)
Integrand prin parti, obtinem
ca
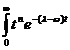 dt =
dt = 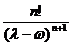 .
.
De aici si
din relatia (1.13), rezulta
ca
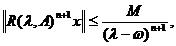
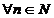 .
.
Corolarul I.4.1. Fie S=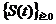 un C
un C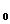 -semigrup pe spatiul Banach X,iar generatorul sau infinitezimal. Atunci
exista M
-semigrup pe spatiul Banach X,iar generatorul sau infinitezimal. Atunci
exista M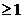 si
si 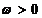 astfel incat
astfel incat
(i)
pentru
orice 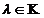 cu Re
cu Re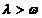 , avem
, avem 
(ii)
pentru
orice 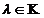 cu Re
cu Re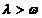 , avem
, avem
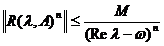 ,
, 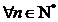 .
.
Demonstratie.
(i) Rezulta din
Corolarul I.3.1.
(ii)
Se obtine din (i) si din Teorema I.4.1.
Teorema I.4.2.(Hille Yosida) Fie A:D(A)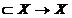 un operator liniar inchis si dens. Daca exista
M
un operator liniar inchis si dens. Daca exista
M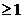 si
si 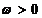 astfel incat
astfel incat
(i) (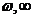 )
) 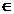
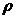 (A);
(A);
(ii) 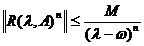 , pentru
orice
, pentru
orice 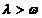 si orice n
si orice n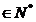
atunci exista un C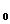 -semigrup S=
-semigrup S=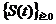 al carui generator infinitezimal este A si cu
proprietatea ca
al carui generator infinitezimal este A si cu
proprietatea ca
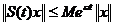 ,
, 
Demonstratie.
Vom face
demonstratia in patru etape.
ETAPA 1. Aratam ca pentru orice x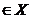 exista
exista 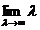 R(
R(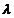 ,A)x=x.
,A)x=x.
Fie x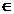 D(A). Din
D(A). Din
R(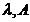 )(
)(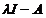 )x = x
)x = x
rezulta ca
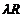 (
(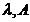 )x = x +R(
)x = x +R(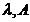 )Ax ,
)Ax , 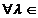
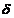 (A).
(A).
Din (ii) deducem ca
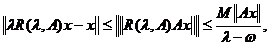
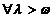 .
.
De aici rezulta ca
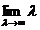 R(
R(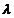 ,A)x=x ,
,A)x=x , 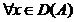 .
.
Cum
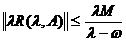 ,
, 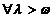
deducem ca exista K > 0 astfel incat
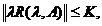
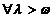
Fie x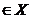 si
si 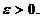 Din faptul ca
operatorul A este dens definit rezulta ca exista y
Din faptul ca
operatorul A este dens definit rezulta ca exista y 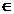 D(A) astfel incat
D(A) astfel incat 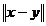 <
< 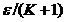 . Atunci din (1.15) avem
. Atunci din (1.15) avem
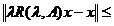
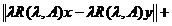
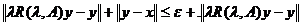 .
.
Astfel conform (1.14) si datorita
faptului ca 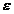 a fost arbitrar,
obtinem
a fost arbitrar,
obtinem
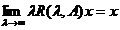 ,
, 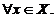 (1.16)
(1.16)
ETAPA
2. Pentru 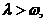 definim A
definim A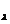 =
= 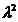 R(
R(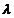 ,A)
,A) 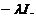 Atunci A
Atunci A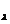
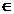 B(X).
B(X).
Fie x 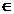 D(A). Rezulta
ca
D(A). Rezulta
ca

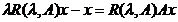
deci
A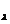 x=
x= 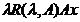 .
.
Din relatia (1.16) deducem ca
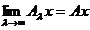 ,
, 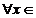 D(A). (1.17)
D(A). (1.17)
ETAPA
3. Fie 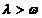 . Pentru fiecare
t
. Pentru fiecare
t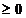 , definim S
, definim S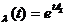 .
.
Rezulta ca
S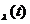 = e
= e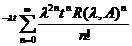 ,
, 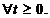
Atunci , obtinem ca
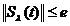
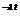
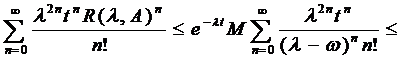
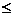
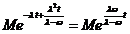 ,
, 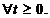
Fie r > 1 . Daca 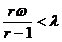 , adica
, adica 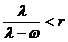 , atunci
, atunci
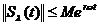 ,
, 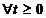 . (1.18)
. (1.18)
Fie x 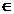 D(A). Deducem succesiv
ca
D(A). Deducem succesiv
ca
S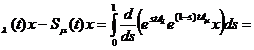
= 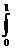 t
t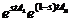 (A
(A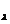 x
x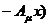 ds=
ds=
=t 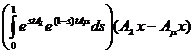 ,
, 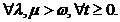
Din (1.18) si
(1.19) deducem ca
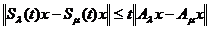
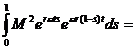
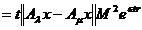 ,
, 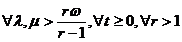 . (1.20)
. (1.20)
Din (1.17) si (1.20) rezulta ca
pentru orice 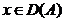 exista
exista 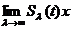 .
.
In plus, aceasta limita este
uniforma in raport cu t pe orice compact
[0,a] cu a > 0 . Din densitatea
lui D(A) in X , tinand seama de relatia
(1.18), se obtine ca pentru orice x 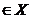 , exista
, exista 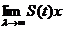 si limita este
si limita este
uniforma in raport cu t pe [0, a], pentru orice a> 0.
Astfel, pentru fiecare t 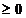 , are sens sa definim
, are sens sa definim
S(t):= 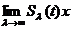 ,
, 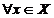 .
.
ETAPA 4. Aratam ca S=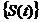
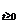 este un C
este un C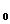 - semigrup, iar A este generatorul sau
infinitezimal.
- semigrup, iar A este generatorul sau
infinitezimal.
Din relatia (1.18) rezulta
ca
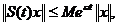
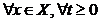 (1.21)
(1.21)
deci S(t) 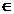 B(X), pentru orice
t
B(X), pentru orice
t 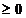 . In plus,
observam ca
. In plus,
observam ca
S(0)x = 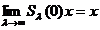 , pentru
orice x, respectiv ca
, pentru
orice x, respectiv ca
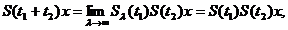
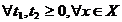
si

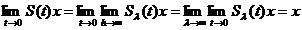 ,
, 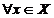 .
.
Obtinem de aici ca S=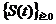 este un C
este un C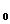 - semigrup.
- semigrup.
Aratam
ca A este generatorul sau infinitezimal.
Fie
B : D(B)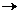 generatorul
sau infinitezimal . Fie x
generatorul
sau infinitezimal . Fie x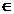 D(A) , t > 0 , si r > 1.
D(A) , t > 0 , si r > 1.
Avem ca
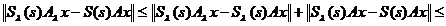
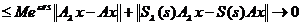 , pentru
, pentru 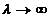
uniform pe [0,t] . Deci 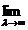
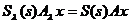 , uniform pe [0,t ]
, pentru orice
, uniform pe [0,t ]
, pentru orice
t > 0, si
orice x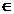 D(A).
D(A).
Deoarece
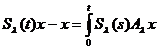 ds ,
ds , 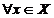
deducem ca
S(t)x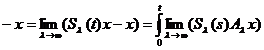 ds =
ds =
=
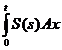 ds ,
ds , 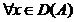
si de aici avem
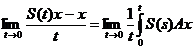 ds = Ax ,
ds = Ax , 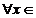 D(A).
D(A).
Rezulta ca D(A) 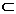 D(B) si Bx
= Ax , pentru orice x
D(B) si Bx
= Ax , pentru orice x 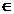 D(A).
D(A).
Reciproc , din relatia (1.21)
rezulta ca daca 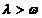 , atunci
, atunci 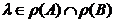 .
.
Deducem de aici ca 
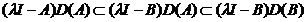
deci
(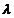 I-B)D(A) = X.
I-B)D(A) = X.
Aplicand
acestei relatii pe 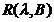 rezulta ca D(A)
= D(B) si astfel A = B , care incheie demonstratia .
rezulta ca D(A)
= D(B) si astfel A = B , care incheie demonstratia .
In
final , deducem teorema de caracterizare a generatorului unui C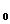 - semigrup.
- semigrup.
Corolarul
I.4.2. (Hille - Yosida ) Fie A : D(A)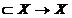 un operator
un operator
liniar inchis si dens definit . A
este generatorul unui C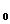 - semigrup S =
- semigrup S = 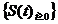 daca si
numai daca exista M
daca si
numai daca exista M 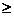 1 si
1 si 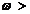 0 astfel incat
0 astfel incat
(i) (  ,
, 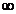 )
) 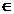
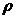 (A);
(A);
(ii) 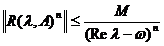 , pentru orice Re
, pentru orice Re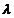 >
>  si orice n
si orice n 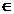
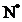 .
.
In plus , in conditiile de mai sus
avem
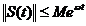 ,
, 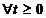 .
.
Demonstratie.
Rezulta imediat din Corolarul I.4.1. si din Teorema I.4.2.


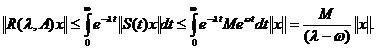
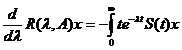 dt (1.12)
dt (1.12)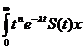 dt
dt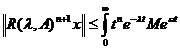 dt
dt 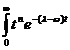
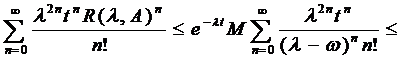
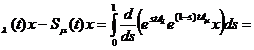
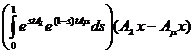 ,
, 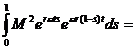
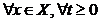 (1.21)
(1.21)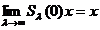 ,
, 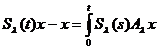 ds ,
ds , 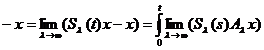 ds =
ds =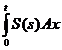 ds ,
ds ,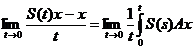 ds = Ax ,
ds = Ax ,