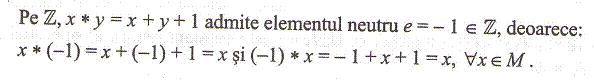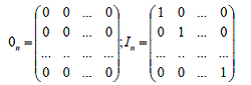Relatii de echivalenta. Partitii.
I)
Definirea
unei relatii si proprietati
O relatie  este definita
prin :-o multime A, numita multime de plecare a lui
este definita
prin :-o multime A, numita multime de plecare a lui 
- o multime B, numita multime de
sosire a lui 
- o parte G a produsului cartezian A x B,
numita
graficul relatiei .
Prin
definitie, spunem ca elementul x  A se afla in relatia
A se afla in relatia  cu elementul y
cu elementul y  B, daca si numai
daca(x ;y )
B, daca si numai
daca(x ;y ) 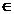 G .
G .
Acest
fapt se scrie : x  y si se citeste ,,elementul x din multimea A
se afla in relatia
y si se citeste ,,elementul x din multimea A
se afla in relatia  cu elementul y din
multimea B. Se spune ca
cu elementul y din
multimea B. Se spune ca  este o relatie de la A la B (sau intre A si B) si se
noteaza cu
este o relatie de la A la B (sau intre A si B) si se
noteaza cu  = ( A,B, G)
= ( A,B, G)
Observatii :
- Din definitie rezulta : G =
- Produsul cartezian a doua multimi defineste
o relatie de la A la B, al carui graf este AxB.
- Graful unei relatii poate fi uneori
vizualizat fie printr o reprezentare cu sageti, fie printr o reprezentare
carteziana.
- Daca A=B, atunci relatia se numeste binara
in A.
- Definitia unei relatii de la
multimea A la multimea B prezinta urmatoarele particularitati : a) un
element din A poate avea mai multe imagini in B. 
b) pot exista
in A elemente care sa nu aiba imagini in B
c) un element din B poate fi imaginea mai
multor elemente din B.
d) poate
exista in B unul sau mai multe elemente care sa nu fie imaginea niciunui elemnt
din A
II )
Proprietati generale ale relatiilor definite intr o multime:
Reflexivitatea:
Definitie: o
relatie  definita pe o multime
A este reflexiva daca pentru orice x din multimea A avem x
definita pe o multime
A este reflexiva daca pentru orice x din multimea A avem x  x.
x.
O relatie binara in AxA este reflexiva
daca graful sau contine diagonala lui AxA.
Exemple : -
in multimea numerelor intregi relatia ,,este mai mic sau egal cu '' este reflexiva deoarece pentru orice x
din Z, se poate scrie x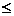 x.
x.
- in
multimea dreptelor din plan, relatia ,,este paralela cu '' este o  relatie reflexiva
relatie reflexiva
Simetria :
Definitie : o relatie  definita pe o multime A se numeste simetrica daca si numai daca pentru orice cuplu (x,y)
definita pe o multime A se numeste simetrica daca si numai daca pentru orice cuplu (x,y) 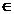 AxA avem x
AxA avem x y
y 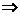 y
y x .
x .
-2-
Exemple : - pe multimea Z definim relatia (x  y)
y)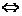 x+y=0, care este o relatie simetrica deoarece x+y=0
x+y=0, care este o relatie simetrica deoarece x+y=0 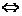 y+x=0.
y+x=0.
3 )Tranzitivitatea :
Definitie :O
relatie  definita pe o multime A se numeste tranzitiva daca si numai daca pentru oricare elemente x,y,z, din A avem (x
definita pe o multime A se numeste tranzitiva daca si numai daca pentru oricare elemente x,y,z, din A avem (x  y si y
y si y  z )
z )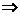 (x
(x  z).
z).
Exemple : - pe multimea Z, relatia ,,este
strict mai mic decat '' este tranzitiva, deoarece pentru orice x,y,z din Z,
avem (x<y si y<z) 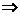 x<z .
x<z .
- pe multimea numerelor naturale
N, relatia ,,este divizibil prin''este o relatie tranzitiva, deoarece pentru
orice x,y,z din N , (x / y si y / z )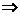 ( x / z)
( x / z)
III ) RELATIA DE ECHIVALENTA
O relatie  definita pe o multime E se numeste relatie de
echivalenta daca :
definita pe o multime E se numeste relatie de
echivalenta daca :
1)  esta reflexiva 1)
esta reflexiva 1) 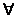 x
x 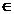 E, x
E, x  y
y
2)  esta simetrica adica 2)
esta simetrica adica 2) 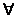 x,y
x,y 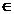 E, (x
E, (x  y)
y)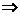 (y
(y  x )
x )
3)  este tranzitiva 3)
este tranzitiva 3) 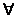 x,y,z
x,y,z 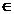 E, (x
E, (x  y) si (y
y) si (y  z)
z)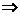 (x
(x  z)
z)
Doua
elemente x si y din E, astfel incat x  y se numesc echivalente in raport cu relatia
y se numesc echivalente in raport cu relatia  .
.
Exemple :
1)Pe multimea dreptelor din
plan relatia ,,a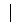
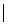 b
b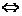 ( a
( a 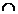 b =
b = 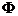 sau a = b) '',unde a
si b sunt drepte din plan , este o relatie de echivalenta.
sau a = b) '',unde a
si b sunt drepte din plan , este o relatie de echivalenta.
2) Pe
multimea E a elevilor din liceu relatia
,,x este coleg de clasa cu y ''este o relatie de echivalenta.
3) Fie
multimea intregilor Z si p 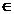 Z
Z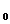 , relatia binara al carui graf G este alcatuit din cuplurile
(a,b) cu proprietatea ca : (a,b)
, relatia binara al carui graf G este alcatuit din cuplurile
(a,b) cu proprietatea ca : (a,b)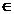 G
G 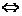 ( a-b)se divide cu p,
este o relatie de echivalenta. Intr
adevar,
( a-b)se divide cu p,
este o relatie de echivalenta. Intr
adevar,
a) a-a este intotdeauna divizibil cu p
b) daca a-b se divide cu p, atunci si b-a se divide cu p.
c) daca a-b si b-c se divid cu p, atunci
si a-c se divide cu p.
Aceasta
relatie de echivalenta in Z se numeste congruenta modulo p si se noteaza cu : a  b ( mod p).
b ( mod p).
4)
Relatia obtinuta intre doua figuri plane atunci cand ele se pot suprapune este
o relatie de echivalenta.(Adjectivul ,,egal''il folosim doar pentru aceeasi figura).
IV )CLASE DE
ECHIVALENTA SI MULTIMEA CAT
Definitie: Fie  o
relatie de echivalenta definita pe multimea E si a
o
relatie de echivalenta definita pe multimea E si a 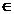 E.
E.
Se
numeste clasa de echivalenta a
elementului a in raport cu relatia  , notata C(a),multimea elementelor din E care sunt
echivalente cu a , adica,
, notata C(a),multimea elementelor din E care sunt
echivalente cu a , adica,
C(a) = .
-3-
Proprietatile
claselor de echivalenta
1) Doua elemente ce apartin aceleiasi clase de echivalenta sunt echivalente intre ele.
2) Clasele a doua elemente
echivalente sunt egale.
3)Doua clase de echivalenta care au
in comun cel putin un element sunt
egale.
4)Relatia  determina o
descompunere a multimii E in multimi
disjuncte, adica o partitie.
determina o
descompunere a multimii E in multimi
disjuncte, adica o partitie.
Definitie :
Se numeste partitie a multimii E orice
familie de submultimi ale lui E cu proprietatile : a) nici o submultime nu este vida
b) oricare doua
submultimi sunt disjuncte
c) reuniunea tuturor
submultimilor este E.
Exemplu :
Fie multimea Z si relatia intre doua elemente a si b din Z, a  b data prin,
b data prin,
,, a -
b este divizibil cu 4 ''
Avem proprietatile : a
) a - a=0, 0= 4k, k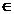 Z - reflexivitatea
Z - reflexivitatea
b) a - b = 4k 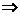 b - a = - 4k, k
b - a = - 4k, k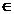 Z -simetria
Z -simetria
c) ( a - b= 4k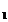 si b - c = 4k
si b - c = 4k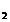 )
) 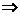 ( a - c = 4k
( a - c = 4k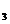 ), unde k
), unde k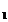 ,k
,k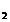 ,k
,k
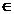 Z
Z
si k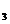 = k
= k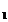 - k
- k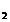 -
tranzitivitatea
-
tranzitivitatea
Relatia
,,a - b este divizibil cu 4'' imparte multimea Z in clase de echivalenta:
C (0) = . C(1) =
C(2) = C(3) =
Multimea
acestor clase se noteaza cu Z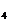 si se numeste multimea cat.
si se numeste multimea cat.
Teorema: Orice relatie de echivalenta intr-o multime E determina o partitie a lui E si
reciproc, orice partitie a lui E determina o relatie de echivalenta in E.
In general, descompunerea
multimii E in submultimi formate din elemente echivalente intre
ele, constituie o partitie: un element
oarecare din E face parte dintr o clasa de echivalenta, relatia fiind reflexiva
pentru orice x din E avem x  x.
x.
Aceste
submultimi sunt nenule, disjuncte si reuniunea lor formeaza multimea E
Un exemplu remarcabil : Relatia de congruenta in Z.
Fie ( Z,+, 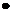 ) multimea numerelor intregi Z, inzestrata cu operatia de adunare si inmultire si fie m
) multimea numerelor intregi Z, inzestrata cu operatia de adunare si inmultire si fie m 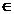 N.
N.
Intre
elementele lui Z introducem relatia ,,a congruent cu b modulo m ''
astfel :
( a  b (mod m))
b (mod m))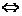 ( m / (a - b ))
( m / (a - b ))
Aceast
este o relatie de echivalenta in Z deoarece :
a) m / (a - a)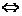 ( a
( a  a ( mod m ) ) -reflexivitate
a ( mod m ) ) -reflexivitate
b) ( a b ( mod m)
b ( mod m)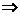 ( m / ( a - b )
( m / ( a - b )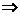 m / ( b - a )
m / ( b - a ) 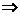 (b
(b  a (mod m ))
a (mod m ))
- simetria
c) [ ( a  b
( mod m) si b
b
( mod m) si b  c ( mod m )]
c ( mod m )]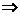 m / ( a - b ) si m / (b - c)
m / ( a - b ) si m / (b - c) 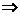
[m / ( a-b +b - c) ] 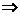 [ m / ( a - c )]
[ m / ( a - c )] 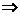 a
a  c (mod m ) - tranzitivitatea
c (mod m ) - tranzitivitatea
-4-
Multimea Z este impartita de relatia de congruenta in clase de echivalenta .
Multimea cat este Z= , iar elementele ei se mai numesc si clase de resturi modulo m.
Relati de congruenta ,,(  mod m )'' este
compatibila cu adunarea, respectiv inmultirea numerelor intregi. Aceast
inseamna ca doua congruente in raport cu acelasi modul se pot aduna membru cu
membru si se pot inmulti membru cu
membru.
mod m )'' este
compatibila cu adunarea, respectiv inmultirea numerelor intregi. Aceast
inseamna ca doua congruente in raport cu acelasi modul se pot aduna membru cu
membru si se pot inmulti membru cu
membru.
Pe aceasta baza se definesc pe multimea
claselor de resturi doua operatii , numite,
,, adunarea ''
respectiv ,, inmultirea '' claselor,
astfel :
a 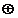 b
b 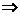 a + b si a
a + b si a 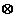 b
b 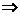 a
a 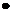 b , unde a si b sunt reprezentantii claselor a si b , iar
b , unde a si b sunt reprezentantii claselor a si b , iar 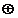 si
si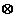 semnifica adunarea si inmultirea claselor.
semnifica adunarea si inmultirea claselor.
Deci, oricare ar fi elementul clasei lui a si
elementul clasei lui b, suma ( respectiv
produsul lor ) apartine
clasei a + b ( respectiv a 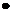 b).
b).
Proprietati
ale legilor de compozitie interna
1. Asociativitatea
Definitie:
O operatie algebrica "* " pe
multimeaM se numeste asociativa , daca:
( x * y ) * z = x * ( y * z ) , x, y, z M
Exemple:
1. Adunarea si inmultirea sunt operatii
asociative pe oricare dintre multimile N, Z, Q, R, C.
2. Adunarea matricelor in multimea. Mnxn(R)
este asociativa .
Pe R se defineste legea * : R x R R , prin x * y = xy -2x - 2y + .
Sa cercetam daca legea * este asociativa:
(x * y) * z = (xy - 2x - 2y + 1) * z = xyz - 2xz - 2yz + z - 2xy + 4x +
4y-2-2z+1 = xyz- 2xy -2xz-2yz + 4x + 4y - z - 1 (*)
x*(y*z) = x* (yz - 2y - 2z + 1) = xyz - 2xy - 2xz +x - 2x - 2yz +4y + 4z
- 2 + 1 = xyz - 2xy - 2xz - 2yz -x + 4y + 4z - 1 (**)
Din (*) si (**) rezulta ca operatia nu este
asociativa.
4. Tot pe R reluand calculele pentru operatia x*y = xy-2x-2y-6 se ajunge
la concluzia ca aceasta este asociativa.
Daca "* " este o operatie pe M, iar H este o
parte a lui M, stabila fata de "* ", atunci: daca "* " este asociativa peM, ea
este asociativa si pe H.
Comutativitatea
Definitie:
O operatie algebrica "* " pe
multimeaM se numeste asociativa , daca:
x
* y = y * x , x, y M


Observatii:
1. Daca "* " este o operatie pe M, iar H este
o parte a lui M, stabila fata de "* ", atunci: daca
"* " este comutativa pe M,
ea este comutativa si pe H.
2. Daca "* " este o operatie pe M data prin tabla operatiei, operatia " " este comutativa daca si numai daca tabla
operatiei
este simetrica fata de diagonala principala.
Distributivitatea
Exemple:
Pe oricare dintre multimile N, Z, Q, R, C sunt definite
operatiile de adunare si inmultire. Legea de compozitie
"inmultirea' este
distributiva fata de "adunare':
a . (b
+ c) = ab + ac, pentru orice a,b,c e N, Z, Q, R, C.
Pe multimea Mn(R) sunt definite adunarea si
inmultirea matricelor. inmultirea este distributiva
fata de adunare:
A . (B + C) = AB + AC, pentru orice A,B,C.
Definitie:
Fie "* " si "s " doua operatii
algebrice pe aceeasi multime M.
Spunem ca operatia "*" este
distributiva la stanga fata de operatia "° ", daca:
(1) x * (y s z) = (x * y) s (x * z),
Spunem ca operatia "* " este
distributiva la dreapta fata de operatia "s ", daca:
(2) (y s z) * x = (y * x) s (z * x),
Spunem ca operatia "* " este
distributiva fata de operatia "° ", daca este
distributiva atat la stanga cat si la dreapta, adica sunt
verificare ambele conditii (1) si (2).
Elementul
neutru
Fie (x, y) x * y o lege de compozitie pemultimeaM.
Spunemca legea admite element neutru
daca exista astfel incat:
x*e = e*x=x , pentru orice
Elementul
e cu aceasta proprietate (daca exista) se numeste element
neutru fata de operatia "*"
Exemplu:
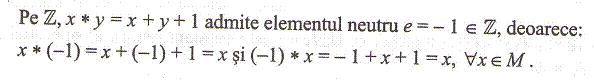

Daca
o lege de compozitie interna admite element neutru, atunci acesta
este unic
in multimea Mn(R) a matricelor patrate de ordinul n
cu coeficienti reali avem legile de compozitie:
adunarea (A, B) A + B si inmultirea (A, B) A . B.
Elementele neutre fata de aceste legi de
compozitie sunt respectiv matricea 0n (matricea zero de ordin n)
si matricea unitate de ordin n care s-a notat cu In :
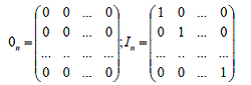

Observatie
In cazul cand legea de compozitie este notata aditiv, elementul neutru este notat cu 0 si se numeste elementul zero.
Daca legea de
compozitie este notatamultiplicativ,
elementul neutru se numeste elementul
unitate.
Sa definim prin inductie compunerea
unui numar finit de elemente din M:


5. Fata de compunerea functiilor
elementele simetrizabile sunt functiile bijective, deoarece o functie
este inversabila daca
si numai daca este bijectiva.
6. Pe multimea R a numerelor reale se
defineste legea de compozitie "* " astfel:
*:RxR R,
x * y = xy - 7x - 7y + 56 al carei element neutru este e = 8.
Cautam elementele simetrizabile.
Fie x e R.. Cautam x' e R
astfel incat x * x' = x' * x = 8 xx' - 7x - 7x' + 56 = xx' - 7x' - 7x + 56
= 8 (deoarece
pe
R adunarea si ".' sunt comutative) xx' -7x-7x' + x'(x - 7) = 7x - 48.
i)
Daca x = 7 ecuatia devine x' . 0 = 1, care nu are
solutie. Prin urmare, x = 7 nu este simetrizabil.
Daca "* ' este o operatie pe M, asociativa cu element
neutru,
notam U(M)
multimea elementelor din M, simetrizabile fata de
operatia
Exemple;
1. Pentru multimea Z inzestrata cu
inmultirea, U(Z) = .
2. Pentru R cu legea x * y = xy - 7x -
ly + 56, dupa cum am vazut anterior, U(R) = R.
3. Pentru, M3(C), inzestrata cu
inmultirea, avem
U(M3(C)) =.
Fie "* " o lege de compozitie interna
asociativa si cu element neutru, definita pe o multimeM.
Atunci:
1°. Daca elementele x,.y sunt
simetrizabile, atunci x * y este simetrizabil si ( x * y )' = y'
* x'
Daca
elementul x este simetrizabil, atunci simetricul sau x' este de asemenea
simetrizabil si ( x' )' = x
Spatii vectoriale
NOTIUNEA
DE SPATIU VECTORIAL
Definitia 1. Se numeste spatiu
vectorial peste un corp K , o
multime nevida V dotata cu doua operatii,
:V
V
V si
: K V V , cu
proprietatile:
I. (V, ) grup abelian;
II. a x x x K x V
b (x y x y K x, y V
c x x K x V
d) 1K
x x x V , unde 1K este
elementul neutru al
operatiei de
inmultire din K .
Exemple de spatii vectoriale:
Rn
, R este spatiul
vectorial numeric real n-dimensional, unde
R
t
n
n
Mm,n R ,R este spatiul
vectorial real al matricelor de tipul
m,n cu elemente numere reale.
R X , R este spatiul
vectorial real al polinoamelor in
nedeterminata X , cu
coeficienti reali.
Rn X
, R este spatiul vectorial real al polinoamelor de grad
cel mult n , in nedeterminata X
, cu coeficienti reali.
F a,b ,
R este spatiul
vectorial real al functiilor reale definite
pe intervalul a,b
Definitia
2. Fie (V,K) un spatiu vectorial si W
V,W
Spunem ca W este subspatiu
vectorial al spatiului vectorial
(V,K) daca:
x,
y W x y W
K, x W
x W
Observatie.
Un subspatiu vectorial are o structura de spatiu
vectorial
in raport cu operatiile induse.
DEPENDENTA SI INDEPENDENTA LINIARA A SISTEMELOR DE
VECTORI
Definitia 1. Fie V,K un spatiu
vectorial. Un sistem finit de vectori n v ,v ,,v 1
2 din V se numeste liniar independent daca n K cu proprietatea 1v1 2v2 nvn 0 , rezulta
n
Definitia 2. Fie V,K un spatiu
vectorial. Un sistem finit de vectori n v ,v ,,v 1
2 din V se numeste liniar dependent daca exista
scalarii n K , nu toti nuli, astfel
incat 1v1 2v2 nvn
Propozitia 1. Un sistem de vectori din
spatiul vectorial Rn , R este liniar
independent daca si numai daca rangul matricei avand pe coloane
vectorii sistemului este egal cu numarul de vectori.
Propozitia 2. Sistemul V este liniar dependent daca
si numai daca cel putin un vector din sistem este o
combinatie liniara a celorlalti.
Propozitia 3. Orice subsistem al unui
sistem de vectori liniar independent este liniar independent.
Propozitia 4. Orice suprasistem al unui
sistem de vectori liniar dependent este liniar dependent.
Propozitia 5. Orice sistem de vectori care
contine vectorul nul este
liniar dependent.