Operatii
cu vectori
Reprezenatrea vectorilor cu sageti ne permite sa dam interpretari geometrice interesanete operatilor cunoscute cu
vectori

 S(x1+x2.Y1+y2)
S(x1+x2.Y1+y2)
A(x1
Y1)
(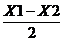 ,
,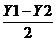 )
)
B.
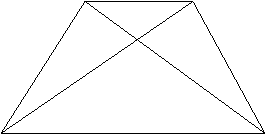
Teormea : Suma vectorilor
Fie vectori OA si
OB cu A(x1 ,y1) ,
B2(x2 ,y2) si suma 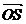 , S(x1+x2.Y1+y2)
, S(x1+x2.Y1+y2)
Segmentul OS este
diagonala paralelogramului cu laturile OA si OB
Demonstartie deoarece mijloacele segmentelor AB si OS au aceelasi
coordonate anume 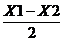 ,
,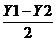 ) , rezulta ca ele coincid , deci AOBS
este paralelogram
) , rezulta ca ele coincid , deci AOBS
este paralelogram
Deci suma vectorilor 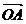 si
si 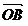 este vectorul
este vectorul 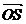 unde S este cel de
al patrulea varf al paralelogramului cu
laturile OA si OB Acest procedeu de obtinere a sumei a doi vectori se numeste
regula paralelogramului
unde S este cel de
al patrulea varf al paralelogramului cu
laturile OA si OB Acest procedeu de obtinere a sumei a doi vectori se numeste
regula paralelogramului
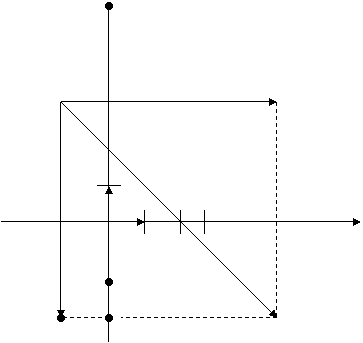
Exemplu
Fie vectori 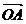 si
si 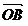 su A(2,1)so B(-1,3)
pentru a gasi suma
su A(2,1)so B(-1,3)
pentru a gasi suma
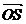 =
= 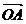 +
+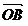 desenam
paralelogramul OASB
desenam
paralelogramul OASB








 y
y
S(1,4)
B(-1,3)
A(2,1)
x
O
Teorema fie
vectorii 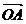 si
si 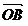 cu A(x1 Y1) , B2(x2
,y2)
cu A(x1 Y1) , B2(x2
,y2)







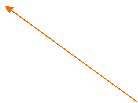
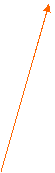


 Diferenta intre
Diferenta intre 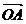 -
-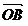 este vectorul
este vectorul 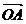 +
+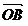 unde B'(-x2'-y2) este simetricul lui b
fata de O
unde B'(-x2'-y2) este simetricul lui b
fata de O
y
A(x1
Y1)
D
B2(x2
,y2)
x
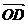 =
=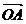 -
-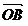
B'(-x2'-y2)
Diferenta dintre 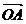 -
-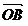 este vectorul
este vectorul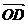 unde D este cel de al doilea patrulater varf al
paralelogramului cu laturile OA si OB'(B este simetricul lui b fata de O)
unde D este cel de al doilea patrulater varf al
paralelogramului cu laturile OA si OB'(B este simetricul lui b fata de O)
Teorema Produsului unui vector cu un scalar
Fie vectorul 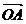 cu A(x1 Y1)
si
cu A(x1 Y1)
si 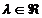
Produsul vectorului 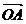 cu scalarul
cu scalarul  este vectorul
este vectorul 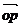 cu proprietatile : OP=
cu proprietatile : OP=  OA si P
OA si P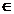 (OA, daca
(OA, daca  >0
>0
P=O, daca  =0
=0
P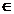 OA-[OA, dac
OA-[OA, dac <0
<0
 y
y
P( x ,
x ,  y)
y)
A(x1
Y1)
 x
x
O
A(x1
Y1)
x
P( x ,
x ,  y)
y)

 Fie vectorul
Fie vectorul 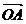 ,A(4,2) pentru a
obtine 3OA gasim punctul p in semidreapta (oa, astfel incat OP= 3OA
,A(4,2) pentru a
obtine 3OA gasim punctul p in semidreapta (oa, astfel incat OP= 3OA
 y
y
 P(12,6)
P(12,6)
A(4,2)
Reprezentarea vectorilor in spatiu
Am reprezentat vectorii (x,y) 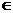 R2 prin puncte sau sageti in plan .Pentru a face acelasi lucru cu vectori (x, y, z)
R2 prin puncte sau sageti in plan .Pentru a face acelasi lucru cu vectori (x, y, z) 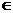 R3 avem nevoie de un reper cartezian (ortogonal) in spatiu
R3 avem nevoie de un reper cartezian (ortogonal) in spatiu
Definitie .Trei axe Ox , Oy Oz cu aceeasi
origine O,perpendiculare doua cate doua , formeaza un reper ortogonal Oxyz in spatiu orientarea axelor se alege
, de obicei asa cum indica sagetile din figura
z

 y
y
o
x
Vectori liberi
s-au definit vectori in functie de un reper
ortogonal dat .In continuare , vom introduce notiune a de vector liber in
plan fara a ne mai baza pe reper , ci flolosind proprietatile geometrice ale
dreptei si planului
definitie se numeste segment arientat o pereche ordonata de puncte din plan .
Segmentul orientat corespunzator perechi de puncate (P,Q) se noteaza cu PQ punctul P situat pe primul loc se numeste origine iar
Q se numeste exterminarea segmentului pq in cazul cand originea se extermitatea coincid se
obtine segmentul orientat nul
Atentie Daca P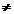 Q aveam PQ=QP
(egali de segmente neorientate )
Q aveam PQ=QP
(egali de segmente neorientate )
Definitie .Dreapta PQ(P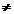 Q) se numeste dreapta
suport a segmentului
Q) se numeste dreapta
suport a segmentului 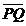 pentru segmentul
orientat nul , dreapta suport este
nedeterminata
pentru segmentul
orientat nul , dreapta suport este
nedeterminata
Marimea (modul) .marimea sau modulul segmentului orientat 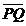 .se noteaza cu PQ sau
.se noteaza cu PQ sau 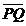 si este lungimea segmentului neorientat PQ.segementul orientat
nul aare marimea zero
si este lungimea segmentului neorientat PQ.segementul orientat
nul aare marimea zero
Directia . daca d este o dreapta
atunci multimea formata din dreapta d si toate dreptele paralele cu d se numeste directia dreptei d
Sens .Pe orice dreapta exista doua
sensuri , corespunzatoare celor doua semi drepte pe care fiecare punct le
determina pe dreapta .
Sensul este indicat de varful unei
sageti
Produsul unui vector cu un numar real
Definitie inmultirea
unui vector cu un numar real .
Produsul dintre vectorul 
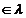 si scalarul
si scalarul 
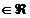 este un nou vector , notat
este un nou vector , notat 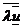 , definit astfel :
, definit astfel :
- Daca 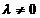 si
si
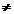
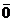 , atunci
, atunci 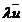 are modulul egal
are modulul egal  x
x  , directia lui
, directia lui  si sensul lui
si sensul lui  pentru
pentru  >0 si sens contrar lui
>0 si sens contrar lui  pentru
pentru  <0 ;
<0 ;
daca  =0 sau
=0 sau  =
=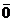 , atunci
, atunci 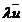 este
este 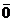 .
.
Exemplu vectorul 2 are distanta si sensul lui
are distanta si sensul lui  , iar modul egal cu
dublu modului lui
, iar modul egal cu
dublu modului lui . Vectorul -
. Vectorul -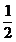
 are directia lui
are directia lui  , sensul contrar lui
, sensul contrar lui  , iar modulul egal cu
jumatate din modulul lui
, iar modulul egal cu
jumatate din modulul lui 



 2
2
 -
-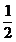

Teorema Proprietatile inmultiri uni vector cu saclar .
- (
(  +
+ )=
)= 
 +
+
 ,
, 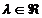
 ,
, g
g
-( +
+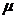 )
)  =
=
 +
+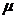
 ,
, 
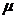
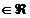

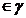
-
( +
+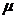 )=(
)=(
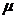 )
)
 ,
,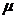
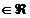 ,
, 
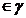
-1  =
= ,0
,0  =
=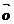

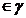
Exerciti :
1 Fie
A si B doua puncte diferite .Demonstreaza ca M este mijlocul segmentului AB
daca si numai daca 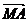 +
+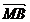 =
=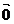
Daca M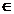 (AB) si AM=MB atunci
(AB) si AM=MB atunci 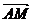 =
=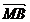 , deci
, deci 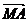 +
+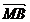 =
=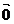
Reciproc .Fie M' mijlocul segmentului AB.
Conform regulii paralelogramului 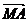 +
+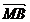 =2
=2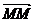 .Deci 2
.Deci 2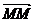 =
=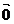 adica M=M' este mijlocul segmentului AB
adica M=M' este mijlocul segmentului AB
2) DOUa Paralelograme ABCD siAB'CD' au diagonala AC comuna .Demonstreaza
vectorialca BB'DD' este paralelogram .
Cum
ABCD este paralelogramul rezulta 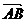 +
+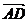 =
=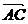
Iar din
faptul ca AB'CD' este paralelogram deducem 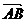 +
+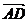 =
=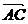 .Asadar avem
.Asadar avem 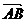 -
-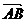 =
=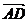 '-
'-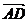 sau
sau 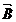 'B=
'B=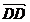 , ceea ce inseamna ca BB'DD' este paralelogram
, ceea ce inseamna ca BB'DD' este paralelogram
Fie triunghiul ABC si A',B'C'
mijloacele laturilor BC , CA si respectiv AB
a)
demonstreaza ca G astefl incat 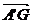 =
=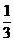
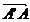 .Arata ca
.Arata ca 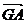 =2
=2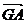 si
si 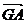 +
+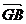 +
+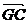 =
=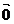
b)
Demonstreaza ca 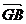 +2
+2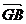 =
=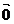 .Arata ca B,C,B' sunt coliniare
.Arata ca B,C,B' sunt coliniare
c)
Arata ca medianele AA' BB' , CC'
sunt concurente



 A
A
 C' B'
C' B'
G
B A C
a) Impartim prin doua puncte segmentu AA' in trei parti egale si notam cu
punctul situat mai aproape de A' .Vectori 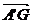 ,
,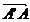 au aceeasi directie acelasi sens si
au aceeasi directie acelasi sens si 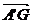 =
=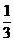
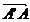 , deci
, deci 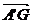 =
=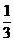
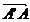 .Avem 3
.Avem 3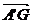 =
=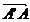 , de unde rezulta 2
, de unde rezulta 2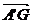 =
=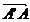 -
-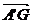
Obtinem -2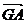 '=
'=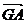 si
si 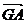 +
+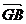 +
+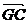 =
=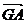 +(
+(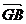 +
+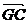 )=
)=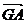 +2
+2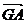 '=
'=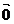
b) Cum B' este mijlocul lui AC rezulta ca 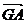 +
+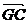 =2
=2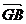 '.Aceasta inseamna ca
'.Aceasta inseamna ca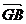 si
si 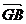 ' au aceasi directie deci B,G,B' sunt coliniare
' au aceasi directie deci B,G,B' sunt coliniare
c) Aratam in mod analog ca C.G.C'
sunt cooliniare .Prin urmare ,
AA',BB',CC sunt sunt concruente in G
Vectori coliniari
Definitie
.Doi vectori sunt coliniari daca cel
putin unul este nul sau daca amndoi sunt ne nuli si au aceeasi directie
Observatie :
din definitie rezulta ca vectorul
nul este coliniar cu orice vector.
Doi vectori necoliniari sunt doi
vectori nenuli care au directi diferite








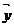
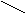



Exemplu
Daca ABCD este trapez cu AB CD si AC BD =atunci vectori 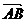 si
si 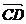 ,
,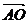 si
si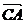 ,
, 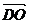 si
si 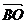 sunt coliniari iar
vectori
sunt coliniari iar
vectori 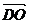 si
si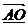 ,
,
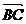 ,
, 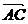 si
si 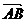 sunt becoliniari
sunt becoliniari
D C
O
A B
Teorema Fie  vector ne nul si
vector ne nul si  un vector oarecare
un vector oarecare
1 Daca  si
si sunt coliniari i exista un nu numar real l , unic
astfel incat
sunt coliniari i exista un nu numar real l , unic
astfel incat  =l
=l
2 Daca existal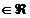 astfel incat
astfel incat  =l
=l , atunci
, atunci  si
si  sunt coliniari
sunt coliniari
Demonstartie
1) Daca  =
= 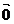 , atunci
, atunci  =
=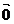 =0
=0 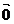
 deci l
deci l
Daca 
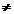
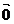 si
si  ,
,  sunt coliniari ,
exista trei puncte coliniare Q,P,R astfel incat
sunt coliniari ,
exista trei puncte coliniare Q,P,R astfel incat

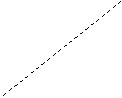


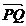 =
= si=
si= .Fie l=
.Fie l=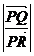 daca
daca 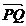 si
si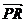 au acelasi sens si l=-
au acelasi sens si l=-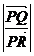 cand
cand 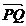 si
si 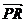 au sensuri diferite
au sensuri diferite


R  P
P  Q
Q
Pentru  astfel ales , vectorul
astfel ales , vectorul 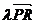 are aceeasi directe , sens si marime ca
are aceeasi directe , sens si marime ca 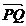 , deci
, deci 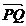 = l
= l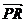 sau
sau  =l
=l
Sa dovedim unicitatea numarului l a carui existenta am demonstrat -o .In acest scop presupem ca ca exista l1 + l 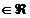 astfel incat
astfel incat  =l
=l  si
si  l
l  .Din aceste egalitai deducem ca l
.Din aceste egalitai deducem ca l  =l
=l  sau ( l l )
sau ( l l )  =
=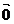 deci l l
deci l l
Exerciti
1 fie  si
si  doi vectori necoliniari .Arata ca :
doi vectori necoliniari .Arata ca :
a)daca
exista x, y 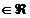 astefel incat x
astefel incat x  + y
+ y =
=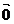 , atunci x=y=0
, atunci x=y=0
b)
daca exista a , b ,a', b' 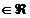 astfel inact a
astfel inact a +b
+b = a
= a =b'
=b'  , atunci a = a' si b=b'
, atunci a = a' si b=b'
rezolvare
Sa presupunem prin reducere la absurd ca x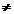 0.Atunci di egalitatea x
0.Atunci di egalitatea x =y
=y =
=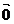 , rezulta ca
, rezulta ca  =-
=-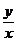
 , deci vectorii
, deci vectorii  si
si  sunt coliniari , ceea
ce contrazice ipoteza .Asa dar , avem x=0. Analog se demonstreaza ca y= o
sunt coliniari , ceea
ce contrazice ipoteza .Asa dar , avem x=0. Analog se demonstreaza ca y= o
b) Relatia data se scrie in forma: ( a-a')  + (b-b')
+ (b-b')  =
=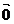 de unde rezulta conform punctului a0 ca a-a' =o si b-b'=0
deci a= a' si b = b'
de unde rezulta conform punctului a0 ca a-a' =o si b-b'=0
deci a= a' si b = b'
Descompunerea unui vector dupa doua directi
date
Dupa directie pot fi definite de doi vectori necoliniari
Teorema .Fie 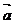 si
si 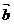 doi vectori
necoliniari .Oricare ar fi vectorul
doi vectori
necoliniari .Oricare ar fi vectorul 
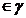 , exista a b
, exista a b 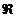 astfel incat
astfel incat  =a,
=a,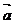 +b
+b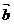 .Scalarii a si b cu
aceasta proprietate sunt unici
.Scalarii a si b cu
aceasta proprietate sunt unici
Exemplu
Fie paralelogramul ABCD cu centrul in O
punctele M
cu centrul in O
punctele M 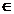 (AB), N
(AB), N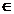 (AD) , astfel incat AM=
(AD) , astfel incat AM=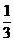 AB si AN =
AB si AN =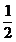 AD
AD
D C



N


 O
O
A M B
Daca 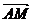 =
= si
si 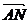 =
= sa descompunem
vectorii
sa descompunem
vectorii 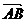 ,
, 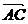 ,
,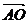 si
si 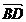 dupa vectori ne
coliniari
dupa vectori ne
coliniari  si
si 
 Definitie Fie xOy un reper cartezian .Consideram punctele A(1, 0) si B(0 ,1) .Vectori
Definitie Fie xOy un reper cartezian .Consideram punctele A(1, 0) si B(0 ,1) .Vectori 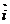 =
=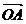 si
si 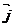 =
=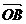 se numesc versorii
axelor de coordonare .Ei au modulul egal
cu 1, Directiile Axelor si sensurile
semiaxelor pozitive Ox si Oy
se numesc versorii
axelor de coordonare .Ei au modulul egal
cu 1, Directiile Axelor si sensurile
semiaxelor pozitive Ox si Oy
B(0,1)
A(1,0)
Exemplu fie Oy un sistem de coordonate
si puncte A(-1,3) , B(4,-2)
Proiectia lui AB pe Ox este pr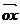 AB=
AB=
Proiectia lui AB pe Oy este pr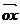 AB=
AB=
A(-1,3) A(0,3) C
J
O
D B (O,-2) B(4-2)
2 IN reperul
cartezian xOy se considera baza Ortonoma
.Reprezinta punctele A, B,C,D, stiind ca 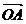 =3
=3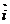 +2
+2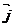 ;
; 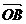 =3
=3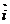 ;
; 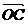 =2
=2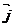 ;
;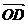 -3
-3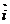 -2
-2
 y
y

 C A
C A
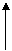











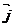
x
 O
O 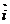
B
D