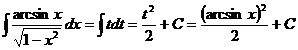METODE DE CALCUL AL INTEGRALELOR
2.
FORMULA SCHIMBARII DE VARIABILA
(SAU METODA SUBSTITUTIEI).
Teorema:
Fie I,J intervale din R si 
1) este derivabila pe I;
este derivabila pe I;
2) f admite primitive. (Fie F o primitiva
a sa.)
Atunci functia (f o )
) ' admite primitive, iar functia F o
' admite primitive, iar functia F o este o primitiva a lui (f o
este o primitiva a lui (f o )
) ' adica:
' adica:
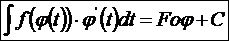
Sa
se calculeze integralele
1. 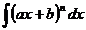 2.
2. 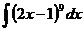 3.
3. 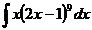
4. 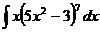 5.
5. 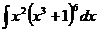 6.
6. 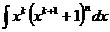
7. 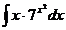 8.
8. 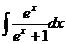
 9.
9. 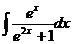
10. 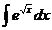 11.
11. 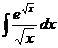 12.
12. 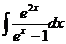
13. 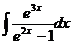 14.
14. 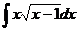 15.
15. 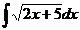
16. 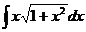 17.
17. 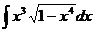 18.
18. 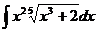
19. 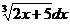 20.
20.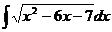 21.
21. 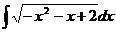
22. 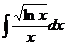 23.
23. 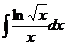 24.
24. 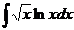
25. 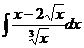 26.
26.
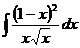 27.
27. 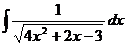
28. 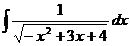 29.
29. 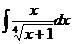 30.
30.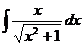 31.
31.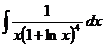 32.
32. 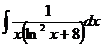 33.
33. 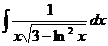 34.
34.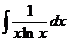 35.
35.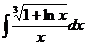 36 .
36 . 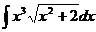 37.
37.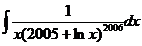 38.
38. 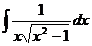
Rezolvari:
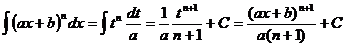 unde ax+b=t
unde ax+b=t 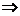 adx=dt dx=
adx=dt dx=
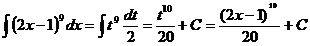 unde 2x-1=t
unde 2x-1=t 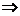 2dx=dt
2dx=dt
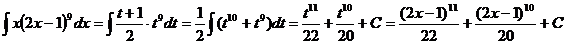
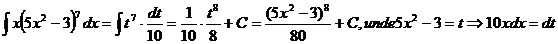
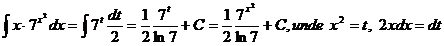
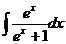
 Notam:
Notam: 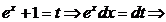

15. 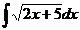 Notam:
Notam: 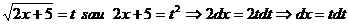
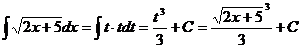
20.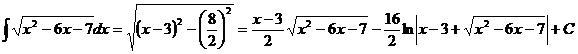 deoarece:
deoarece: 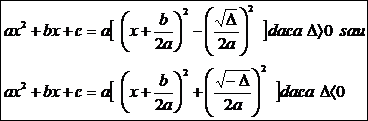
23. 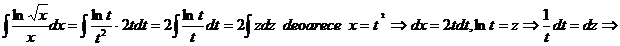
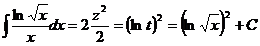
28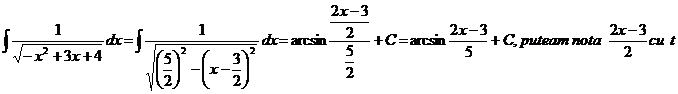
INTEGRAREA FUNCTIILOR TRIGONOMETRICE
Calculul integralelor trigonometrice se poate
face fie folosind formula
integrarii prin parti, fie metoda substitutiei.
In acest caz se pot face substitutiile:
1. Daca functia este impara in
sin x, R(-sin x,cos x)=-R(sin x,cos x) atunci cos x=t.
2. Daca functia este impara in
cos x, R(sin x,-cos x)=-R(sin x,cos x) atunci sin x=t.
3. Daca functia este para in
raport cu ambele variabile R(-sin x,-cos x) atunci tg x=t.
4. Daca o functie nu se
incadreaza in cazurile 1,2,3,atunci se utilizeaza substitutiile
universale:
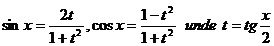
5. Se mai pot folosi si alte formule
trigonometrice:
sin 2x=2sin x .cos x, 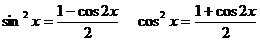
Sa
se calculeze:
1.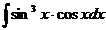 2.
2. 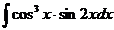 3.
3.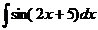
4. 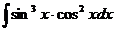 5.
5. 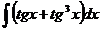 6.
6. 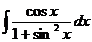
7. 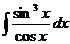 8.
8. 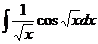 9.
9. 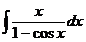
10.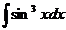 11.
11.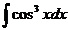 12.
12.
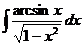
13.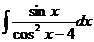 14.
14.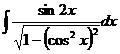 15.
15.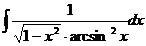
16.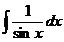 17.
17.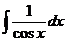 18.
18. 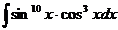
19.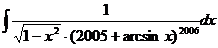 20.
20. 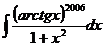
Rezolvari:
Notam sin x=t 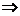 cosx dx= dt
cosx dx= dt 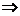
2. Notam cos x=t 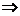 -sin x dx=dt
-sin x dx=dt
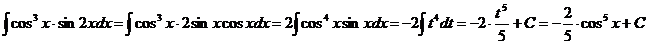
10. 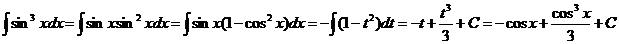 12.
12. 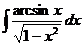 Notam cu t pe
arcsin x
Notam cu t pe
arcsin x 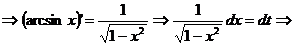
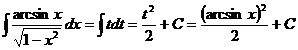


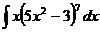
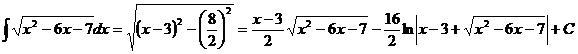
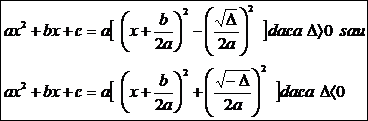
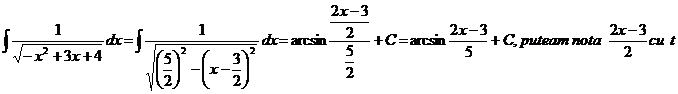
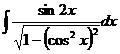 15.
15.