Matematica si muzica

MATEMATICA si MUZICA

Muzica, arta care exprima cu ajutorul sunetelor sentimente si stari psihice, sunete combinate melodios si armonic spre a fi placute auzului, a aparut de timpuriu in istoria culturii; de muzica a dispus omul inainte de a articula cuvinte, poate din paleolitic, sigur din neolitic. Ea se bazeaza pe suntete produse de vibratiile regulate ale corpurilor elastice, adica pe sunete muzicale (muzica electronica moderna foloseste insa, uneori, pe langa sunete muzicale, si zgomote, adica vibratii neregulate; iar asa-numita muzica abstracta utilizeaza cu precadere zgomote).

Acum 2500 de ani, Pitagora s-a servit de un instrument numit monocord (o singura coarda vibranta), care este analog cu sonometrul utilizat astazi pentru studiul vibratiilor coardelor. Utilizand acest monocord, Pitagora si-a dat seama, cel dintai, ca sunetul muzical (sau cel vorbit) este rezultatul vibratiilor regulate ale corpurilor elastice. De asemenea, Pitagora a constat ca atunci cand vibreaza impreuna doua coarde, dintre care una este de doua ori mai lunga decat cealalta, se aud doua sunete, coarda mai scurta dand sunetul cel mai inalt. Sunetul cel mai inalt produs de coarda scurta este in octava fata de sunetul cel mai jos produs de coarda dubla. Prin urmare, daca cele doua coadre au raportul lungimilor lor 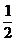raportul frecventelor sunetelor emise este 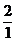, adica rapoartele lungimilor si ale frecventelor sunt inverse unul altuia. Tot Pitagora a constatat ca daca lungimile coardelor sunt in raportul 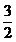, sunetele ce se aud formeaza intervalul muzical numit cvinta; iar raportul 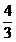da intervalul numit cvarta. In felul acesta evaluarea simpla si precisa in rapoarte de numere intregi ale celor trei intervale considerate consonante perfecte, octava, cvinta si cvarta, perfecte, a constituit baza sistemului muzical. Precizandu-se aceste trei intervale de baza de catre Pitagora si discipolii sai, s-a putut fixa ulterior gama (scara) diatonica greaca (scara lui Pitagora), ale carei sunete (note) au fost numite ulterior do, re, mi, fa, sol, la ,si, do. Englezii, olandezii, germanii si ungurii desemneaza cele 8 suntele ale octavei prin litere:

Prin urmare, Pitagora si discipolii sai si-au dat seama ca in succesiunea sunetelor (notelor) muzicale intervin rapoarte constante din nunmere intregi ca 1,2,3,4.

Mai tarziu, s-a vazut ca daca vom considera egala cu unitatea lungimea sonometrului care produce pe do, lungimile pentru celelalte note sunt mai mici decat 1, dar totdeauna exprimate prin numere rationale ca rapoarte de numere intregi. Si anume, s-a gasit ca pentru scara muzicala a lui Pitagora, avem urmatoarea corespondenta:

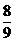
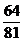
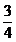
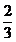
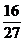
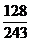
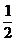
Aceasta scara muzicala a lui Pitagora este convenabila pentru scrierea melodica a unei lucrari muzicale, dar nu-i satisfacatoare pentru scrierea armonica; de aceea, ea nu a fost folosita decat pana la sfarsitul evului mediu, mai ales de catre compozitorii cantecelor bisericesti. Aparand necesitatea polifoniei si dezvoltandu-se scrierea armonica s-a gasit ca daca in scara lui Pitagora, intervalele de la do la mi, fa la la si sol la si se vor restrange, se va obtine o intonatie mult mai placuta, mult mai satisfacatoare. In acest fel, toate tertele majore fa -la -do, sol- si - re, do - mi -sol devin terte majore perfecte in raportul 4 : 5 : 6.

Noua scara, dandu-se seria sunetelor armonice, a fost numita, de aceea, scara (gama) majora cu intonatie justa sau scara muzicala naturala.

Cei vechi aveau un instrument muzical mult folosit in reprezentatiile muzicale : lira cu 8 coarde vibrante. La aceasta lira s-au determinat raportele dintre doua sunete muzicale, precum tonul, semitonul, cvarta, cvinta, octava. Un interval muzical, distanta dintre doua sunete sau doua note muzicale, poate fi reprezentat aritmetic prin catul dintre frecventa sunetului muzical mai acut si frecventa sunetului muzical mai grav. Aceasta inseamna, experimentandu-se in alt mod matematic, ca logaritmul unui interval oarecare este egal cu logaritmul frecventei notei mai inalte minus logaritmul frecventei notei mai joase. Dar un logaritm poate fi exprimat si ca o suma de logaritmi ai intervalelor componente (ceea ce inseamna, in acest caz, ca intervalul poate fi determinat aritmetic ca un produs de numere).

Tonul este intervalul muzical dintre doua note consecutive ale gamei diatonice grecesti ( afara de intervalul dintre mi si fa sau cel dintre si si do). Semitonul este intervalul de o jumatate de ton, ca de exemplu, intre mi si fa sau si si do.

Prima este intervalul dat de aceeasi nota repetata, de exemplu do₁ - do₁, distanta zero data de aceeasi treapta; secunda este distanta dintre doua sunete alaturate, de exemplu, do -re, mi -fa etc.; terta este intervalul dintre trei trepte consecutive, de exemplu, do - mi, sol - si etc.; cvarta consta din patru trepte, deci intervalul dintre sunetele 1 si 4 (de exemplu do - fa); cvinta consta din cinci trepte, deci intervalul dintre sunetele 1 si 5 (de exemplu, do - sol), si asa mai departe; octava este intervalul dintre prima si ultima nota cu acelasi nume dintr-o gama (de exemplu, do- do₁).

Unisonul are raportul egal cu 1, dar octava este caracterizeaza prin ra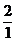portul , adica do de sus si do de jos din aceeasi octava au frecventele lor in raportul .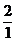

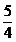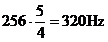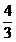Terta majora inseamna raportul ;daca do₃ are 256 Hz, atunci mi₃ din scara majora naturala are . Tot asa, cvarta perfecta inseamna raportul si este inversa unei cvinte perfecte, Aceasta din urma insemnand raportul 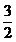, pentru raportul cvartei perfecte putem scrie:

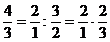
Astfel spus, o cvarta perfecta si o cvinta perfecta ne dau o octava, adica

,

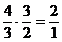ca rapoarte de numere intregi. Sau logaritmic putem scrie :

,

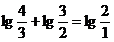De unde

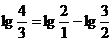
ceea ce se citeste: logaritmul cvartei perfecte este egal cu logaritmul octavei minus logaritmul cvintei perfecte.

Logaritmii sunt descoperiti insa de Neper, putin dupa anul 1600 e.n., astfel incat in scoala lui Pitagora (sec. VI - V i.e.n.) nu s-a stiut de legatura logaritmica dintre diferitele intervale.

Caracterizam matematic, mai departe, cateva din intervalele muzicale cele mai importante:

Sexta majora inseamna raportul 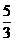si este egala cu o cvarta perfecta o terta majora, deoarece :

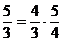
Sau, aplicand logaritmii :

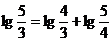
adica logaritmul sextei majore marite este egal cu suma logaritmului cvartei perfecte si cel al tertei majore.

Terta mica (minora) inseamna pentru raportul frecventelor celor doua sunete valoarea 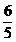si este intervalul prin care o cvinta intrece o terta majora deoarece:

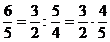
Altfel spus, o terta minora mica plus o terta majora ne dau o cvinta perfecta, deoarece :

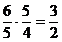
si aplicand logaritmii:

.

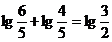Sexta mica (minora) este reprezentata prin raportul 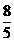si este egala, logaritmic, cu suma unei cvarte perfecte si a unei terte minore micsorate, adica :

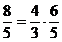
sau

.

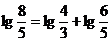Sexta minora micsorata este inversa tertei majore, deoarece avem :

.

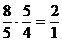Septima mica ( minora) este reprezentata prin raportul 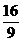si este egala, logaritmic, cu suma a doua cvarte perfecte.

Intr-adevar, avem :

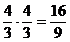
Acesta este un interval disonant.

Septima majora este reprezentata prin raportul frecventelor dat de 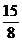si este egala cu suma unei cvinte perfecte si a unei terte majore, deoarece avem :

.

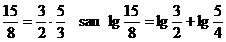Fara a mai da si alte exemple , logartmii pot fi folositi spre a preciza intervalele muzicale, pentru ca, spre a gasi logartmul unui interval muzical dat, nu avem altceva de facut decat de adunat sau de scazut logaritmii altor intervale.

Dar se pot stabili legaturi si intre muzica si matematica moderna abstracta. Intr-adevar, frecventele tonurilor pure muzicale formeaza o multime de numere reale distribuite intre limitele inferioare si superioare ale auditibilitatii (16Hz, respectiv 20000Hz). Notele pianului formeaza o submultime finita din spectrul infinit al sunetelor, submultime care contine, obisnuit, numai 88 de elemente (88 clapete). La instrumentele cu coarde (vioara, etc.) si la trombon, avem de-a face cu o submultime infinita de sunete; la celelalte instrumente avem insa numai submultimi finite de sunete discrete muzicale.

Cand avem doua note, una infierioara de frecventa a si alta superiaora de frecventa b, intre ele avem, in realitate, o relatie de preordine b>a, antisimetrica si tranzitiva. Apoi, notele pot fi impartite in clase de echivalenta, printr-o relatie de echivalenta: doua note sunt echivalente cand sunt separate exact printr-o octava.

In sfarsit, ca sa terminam cu legatura dintre muzica si matematica moderna, consemnam ca daca se canta la un instrument muzical oarecare, modelul matematic care poate reprezenta sunetele ne este dat de un spatiu vectorial.

In armonie, cand este vorba de dublarea sau de suprimarea sunetelor in acorduri , rasturnari de acorduri, de intarzieri sau suspensii, anticipatii, broderii, apogiaturi, cadente, acorduri de septima dominanta sau de nona majora, alteratii coboratoare, acorduri de undecima, modulatii, imitatii, progresii armonice etc., toate acestea nu se fac oricum, ci dupa anumite reguli bine stabilite si precis respectate de compozitori; dar regulile acestea inseamna calcul matematic. Si tot astfel fuga in muzica, adica lucrarea polifonica in care are loc repetarea imitativa a unuia sau doua subiecte dupa un anumit plan tonal-armonic, atat de intalnita la Bach si Handel, nu se intocmeste oricum, ci tot dupa reguli matematice, pe care compozitorii trebuie sa le stapaneasca aproape intuitiv.

Numai matematica singura insa nu este capabila sa explice totul in muzica. Nu se va ajunge niciodata sa se scrie muzica cu ajutorul simbolismului matematic ca, de exemplu, muzica in ecuatii. Dar muzica poate fi tratata prin mijlocirea matematicii, aceasta dandu-i un fundament solid de mare profunzime. In sprijinul acestei idei, calculatoarele pot fi folosite la mecanizarea orchestratiilor compozitiilor muzicale. In scrierea programelor, intervin legile armoniei.

Una din dovezile cele mai impersionante pentru legatura dintre muzica si matematica a gasit-o matematicianul Goncearov, prin studii privind ecuatii cu derivate partiale, un acord cu totul nou, extrem de placut, aceasta putand duce la constructia de instrumente muzicale noi.

Cine studiaza istoria matematicii constata ca Gh. Titeica, Dimitrie Pompeiu, Traian Lalescu si Petre Sergescu cantau la vioara, Victor Valcovici la flaut, Mihail Ghermanescu la violoncel. Toti acestia nu erau simpli diletanti, ci executanti foarte buni ai compozitiilor muzicale clasice. La Paris era arhicunoscut un cvartet desavarsit, din care faceau parte matematicienii Henri Poincare si C.A. Laisant, cvartet care interpreta in special pe L.van Beethoven.

Si in muzica intervine, ca si in poezie, cadenta si masura; numai asa se asigura trainicia si estetica operelor muzicale. Cum cadenta si masura inseamna matematica, iata legatura stransa dintre arta care poate exprima toate sentimentele omenesti si stiinta certitudinii.

Spre a incheia, sa reamintim cele spuse de marele matematician Sylvester :

"Nu s-ar putea oare reprezenta muzica drept matematica a simturilor si matematica drept muzica a ratiunii? Caci muzicianul simte matematica, iar matematicianul concepe muzica. Muzica-i vis, matematica viata practica" !