Grafuri planare
1.
Definitii si proprietati
Pentru a
reprezenta unele structuri geometrice in plan sau in spatiu se
foloseste o categorie speciala de structuri de date: grafuri planare.
Definitia 1. Un graf G este planar daca este
posibil sa fie reprezentat pe un plan astfel incit virfurile sa fie
distincte, muchiile curbe simple si doua muchii sa nu se
intersecteze decit la extremitatile lor (daca sint adiacente).
Reprezentarea
grafului conform cu conditiile impuse se numeste graf planar
topologic si se noteaza tot prin G. Nu se considera distincte doua grafuri planare
topologice daca le putem face sa coincida prin deformarea
elastica a planului.
Definitia 2. O fata a
unui graf planar este o regiune a planului delimitata de muchii, care
are proprietatea ca orice doua puncte din aceasta regiune pot fi
unite printr-o curba simpla care nu intilneste nici muchii
si nici virfuri.
Definitia 3. Frontiera unei
fete este multimea muchiilor care ating fata
respectiva. Doua fete sint adiacente daca frontierele lor
au cel putin o muchie comuna.
Intr-un graf
topologic, frontiera unei fete este formata din unul sau mai multe
cicluri elementare disjuncte, din muchii suspendate sau care unesc doua
cicluri disjuncte (istmuri).
Definitia 4. Conturul unei
fete este conturul ciclurilor elementare care contin in
interiorul lor toate celelalte muchii ale frontierei.
Exista
intotdeauna o fata infinita si care are frontiera, dar
nu are contur; toate celelalte fete sint finite si admit un contur.
Teorema 1 (Euler). Intr-un graf planar
topologic conex cu n virfuri, m muchii si f fete avem relatia:
n - m f 2
Demonstratie (Tomescu - 1981, pg
203-204). Daca f 1 atunci m n-1 pentru un arbore (teorema 6.2), deci relatia este
adevarata.
Presupunem
afirmatia adevarata pentru orice graf planar conex cu f
-1 fete, si sa consideram un graf planar conex cu f fete. Fie (x,y) o muchie a unui
ciclu; aceasta se afla pe frontiera a doua fete S si T. Daca eliminam muchia (x,y) se obtine un
graf planar conex cu n' n virfuri, m' m-1 muchii si f' f -1 fete.
Conform ipotezei de inductie n'-m' f n-1-m 1 f 2, de unde obtinem ca
n-m f 2. n
Corolar 2. In orice graf planar
topologic conex cu n virfuri, m muchii si f fete avem:
(i) n
2m/3 ; m 3f-6 ; n 2f-4
(daca
fiecare virf are gradul cel putin trei)
(ii) f 2m/3 ; m 3n-6 ; f 2n-4
(daca graful are cel putin doua muchii)
Demonstratie. (i) Din fiecare virf
pleaca cel putin trei muchii, si fiecare muchie uneste
doua virfuri; rezulta 3n 2m. Celelalte doua
inegalitati rezulta prin simpla inlocuire.
(ii) Daca m 2 atunci f 1 si n 3. Daca f 1 si m > 2 atuncin m 1. Daca f 2 atunci fiecare
fata are cel putin trei laturi (muchii), si o muchie este
comuna la cel mult doua fete; rezulta 3f 2m. Celelalte doua inegalitati rezulta prin
simpla inlocuire. n
Sa
consideram in spatiul tridimensional un poliedru convex cu n virfuri, m muchii si f
fete. Putem sa-l reprezentam pe o sfera astfel incit
doua muchii sa nu se intersecteze decit la extremitati.
Efectuind o proiectie stereografica al carei centru sa fie
in mijlocul unei fete, poliedrul se poate reprezenta pe un plan. Graful
fiind planar, se obtine relatia lui Euler n m f 2.
Sa
consideram un graf planar topologic conex G, caruia ii facem sa-i corespunda un graf planar
topologic G* astfel:
- in interiorul
fiecarei fete s din G plasam un punct x* din G*;
-
fiecarei muchii u din G ii facem sa-i corespunda o
muchie u* din G* care uneste virfurile x*
si y* corespunzatoare
fetelor s si t situate de o parte si de alta a
muchiei u.
Graful G* este de asemenea planar (figura 1).
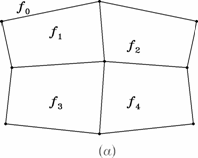
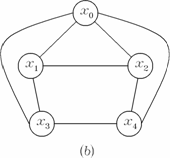
Figura 1. Un graf
planar (a) si dualul sau (b).
2. Reprezentarea unui graf planar
In continuare
prezentam o descriere simplificata a unei structuri de date
(Preparata, Shamos) (de Berg et al), folosita pentru reprezentarea in
memorie a unui graf planar.
Sa
consideram o diviziune a planului indusa de un graf planar in care
muchiile sint segmente de dreapta (PSLG - planar straight line graph). Consideram de asemenea ca o
muchie este deschisa, adica virfurile nu apartin muchiei. O fata a diviziunii este o
multime conexa maximala care nu contine nici un punct pe
muchie si nici un virf; o fata este deci o regiune
poligonala deschisa a carei frontiera este formata din
muchii si virfuri ale diviziunii. Complexitatea diviziunii este
definita ca suma dintre numarul de virfuri, numarul de muchii
si numarul de fete care o compun. Daca un virf este
capatul unei muchii, spunem ca virful si muchia sint incidente,
de asemenea o fata si un virf de pe frontiera sint
incidente.
O astfel de
reprezentare a diviziunii este utila, de exemplu, pentru a parcurge
frontiera unei fete date, sau pentru a determina o fata
adiacenta alteia fiind data o muchie comuna. Reprezentarea
discutata in continuare suporta toate aceste operatii; aceasta
este numita lista de muchii
dublu conectata (DCEL - doubly
connected edge list).
O lista
de muchii dublu conectata se compune din cite o inregistrare pentru
fiecare fata, muchie si virf al subdiviziunii. Informatiile
despre geometria si topologia diviziunii memorate in lista trebuie
sa permita operatiile de baza mentionate mai sus.
Pentru a putea parcurge frontiera unei fete in sens trigonometric memoram
un pointer de la fiecare muchie la urmatoarea. O muchie este
incidenta de regula la doua fete, astfel ca este
convenabil sa vedem cele doua orientari ale unei muchii ca
si doi vectori distincti.
Avem deci un singur vector urmator si un singur vector precedent
pentru fiecare vector. Aceasta inseamna ca un vector este incident la
o singura fata. Cei doi vectori pe care ii obtinem dintr-o
muchie se numesc gemeni. Definirea
vectorului urmator al unui vector in raport cu o parcurgere in sens
trigonometric a unei fete pe care o margineste induce o orientare
pentru fiecare vector: un vector este orientat astfel incit fata pe care o
margineste se afla in stinga pentru un observator aflat pe
muchie. Deoarece un vector este orientat putem vorbi despre originea si
destinatia acestuia. Daca un vector  are virful x ca origine si virful y ca destinatie, vectorul
geaman are virful y ca origine
si virful x ca destinatie.
Pentru a regasi frontiera unei fete avem nevoie sa memoram
in inregistrarea fetei un pointer catre un vector oarecare care
margineste fata. Incepind cu acest vector putem determina
urmatorul vector si astfel sa parcurgem fata.
are virful x ca origine si virful y ca destinatie, vectorul
geaman are virful y ca origine
si virful x ca destinatie.
Pentru a regasi frontiera unei fete avem nevoie sa memoram
in inregistrarea fetei un pointer catre un vector oarecare care
margineste fata. Incepind cu acest vector putem determina
urmatorul vector si astfel sa parcurgem fata.
In concluzie, lista de muchii dublu
conectata se compune din trei colectii de inregistrari: una
pentru virfuri, una pentru fete si una pentru vectori. Aceste
inregistrari memoreaza urmatoarea informatie
geometrica si topologica:
- inregistrarea de tip virf memoreaza
coordonatele unui virf x, si
eventual un pointer spre unul din vectorii care au originea in acest virf;
- inregistrarea de tip fata
memoreaza un pointer spre inregistrarea unui vector oarecare incident la
fata respectiva; o fata este descrisa ca o lista
circulara inlantuita de vectori;
- inregistrarea de tip vector a unui
vector 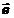 memoreaza doi
pointeri spre virfurile origine si destinati, un pointer spre
geamanul sau, si un pointer spre fata Fata(
memoreaza doi
pointeri spre virfurile origine si destinati, un pointer spre
geamanul sau, si un pointer spre fata Fata(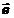 ) pe care o margineste; originea lui
) pe care o margineste; originea lui  se alege astfel incit
fata incidenta sa se afle la stinga daca vectorul este
parcurs de la origine la destinatie; se memoreaza de asemenea un
pointer catre vectorul urmator Urm(
se alege astfel incit
fata incidenta sa se afle la stinga daca vectorul este
parcurs de la origine la destinatie; se memoreaza de asemenea un
pointer catre vectorul urmator Urm( ), care margineste aceeasi fata ca
si
), care margineste aceeasi fata ca
si  .
.
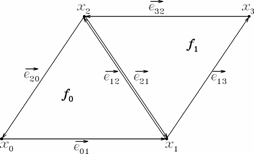
Figura 2. Lista de
muchii dublu conectata.
Virf Coord Fata Un vector incident
x0 (-3,-2) f0 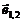
x1 (1,-2) f1 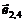
x2 (-1,2)
x3 (3,2)
Vector Origine Destinatie Geaman Fata Urm
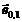 x0 x1 - f0
x0 x1 - f0 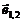
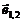 x1 x2
x1 x2 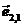 f0
f0 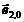
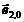 x2 x0 - f0
x2 x0 - f0 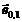
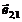 x2 x1
x2 x1 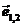 f1
f1 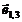
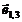 x1 x3 - f1
x1 x3 - f1 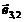
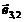 x3 x2 - f1
x3 x2 - f1 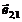
In multe
probleme practice nu avem nevoie ca regiunea infinita sa fie
memorata in mod explicit. Un caz de exceptie este de exemplu
reprezentarea unui poliedru convex, unde una din fete (nu are
importanta care, nici nu se precizeaza in reprezentare) este
considerata a fi infinita. In exemplul din figura 2 am memorat in
lista doar cele doua regiuni finite ale domeniului: f0 si f1, impreuna cu cei
sase vectori incidenti acestor fete.
3. Planificarea traiectoriei unui robot
Unul dintre
scopurile finale ale roboticii este proiectarea unor roboti autonomi:
roboti carora sa le spunem ce
sa faca fara sa fie nevoie sa le spunem cum sa faca. Printre altele,
un robot trebuie sa-si poata planifica miscarea. Pentru
aceasta robotul trebuie sa aiba cunostinte despre mediul in
care se va deplasa. De exemplu, un robot mobil care se deplaseaza in jurul
unei fabrici trebuie sa stie unde sint localizate obstacolele.
Folosind informatii despre mediu robotul trebuie sa ajunga
intr-o pozitie finala evitind coliziunea cu orice obstacol.
Problema
generala a planificarii miscarii este destul de
dificila, de aceea facem o serie de simplificari. Considera problema
planificarii miscarii in plan, astfel ca mediul este o
regiune planara compusa din obstacole de forma poligonala.
In prima etapa consideram ca robotul este un punct, iar in a
doua un disc. Presupunem de asemenea ca mediul este static - nu
exista obstacole mobile - si cunoscut in intregime de robot. Aceste
restrictii nu sint chiar asa de severe cum ar parea la prima
vedere: pentru un robot care se deplaseaza intr-un mediu planar de lucru, o
modelare a acestuia (poligoane pentru ziduri, mese, masini s.a.) este
adesea suficienta.
Miscarile
pe care le poate efectua un robot sint stabilite in momentul proiectarii
acestuia: unii roboti se pot deplasa in orice directie, se pot roti
in jurul unei axe, in timp ce altii au limitari destul de severe (de
exemplu o masina trebuie sa se deplaseze paralel cu frontiera
unui obstacol).
Fie un robot
punctual R si o multime de
obstacole poligonale S := , numarul total de
virfuri fiind n. Pentru inceput
construim o structura de date care memoreaza o reprezentare a
spatiului liber (in care robotul se poate deplasa). Aceasta poate fi
ulterior folosita pentru a determina o traiectorie intre oricare doua
puncte date: cel de plecare (start) si cel destinatie (terminus).
Pentru a
simplifica descrierea restringem deplasarea robotului la o zona
dreptunghiulara B care
contine multimea poligoanelor. Cu alte cuvinte, adaugam un
extra-obstacol infinit care este zona aflata in exteriorul dreptunghiului B. Spatiul liber este acel fragment
al zonei B neacoperit de nici
un obstacol:
Free(S ) = B
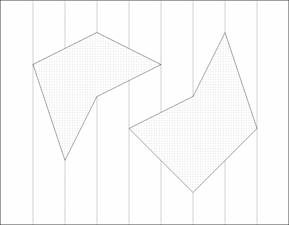
Figura 3. O
subdiviziune trapezoidala a spatiului liber.
Pentru
reprezentarea spatiului liber se foloseste o structura de date
numita harta trapezoidala
(trapezoidal map, figura 3). Aceasta este o subdiviziune a planului
formata din trapeze, care se poate determina folosind un algoritm bazat pe
tehnica de scanare a planului.
O harta
trapezoidala poate fi determinata intr-un timp de ordin O(n log n)
(Preparata, Shamos) (de Berg et al). Deoarece ordinul de marime a
hartii (numarul de trapeze) nu depaseste ordinul
de marime al unei diagrame Delaunay (a se vedea capitolul 6), rezulta
ca harta are o marime de ordin O(n), deci
liniar.
Ramine
un detaliu de rezolvat: cum se foloseste Free(S ) pentru a
gasi o traiectorie intre un punct ps
si un punct pt?
Daca cele doua puncte se afla in acelasi trapez, robotul se
deplaseaza pur si simplu din ps
in pt.
In cazul in
care cele doua puncte se afla in trapeze diferite, traiectoria va
traversa un anumit numar de trapeze si va avea un anumit numar
de schimbari de directie. In acest scop construim un graf G care reprezinta harta drumurilor libere. Acesta este un graf planar ale carui
noduri si arce se afla in spatiul liber Free(S ). Cu
exceptia punctului de start si a punctului terminus, orice
traiectorie va urma intotdeauna aceasta harta. Sa observam
ca orice doua trapeze vecine partajeaza o muchie verticala,
fapt care conduce la definirea hartii dupa cum urmeaza.
Plasam cite un nod in centrul fiecarui trapez, si de asemenea
cite un nod in mijlocul fiecarei muchii comune la doua trapeze. In
continuare definim arce intre doua noduri daca si numai
daca un nod este centrul unui trapez si celalalt este pe
frontiera aceluiasi trapez. Arcele se reprezinta grafic ca si
segmente de dreapta, astfel ca parcurgerea unui arc de pe harta
corespunde unei deplasari in linie dreapta a robotului. Harta
drumurilor poate fi construita intr-un timp de ordin O(n) prin traversarea
listei de muchii dublu conectate corespunzind la Free(S ). Folosind
arcele din harta drumurilor ne putem deplasa dintr-un nod aflat in centrul unui
trapez in nodul aflat in centrul unui trapez vecin via nodul aflat pe muchia
comuna.
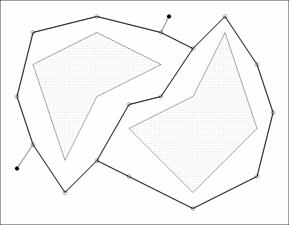
Figura 4. Determinarea hartii drumurilor libere
Putem folosi
harta drumurilor, impreuna cu harta trapezoidala, pentru a planifica
deplasarea intre doua puncte (figura 4). Mai intii determinam
trapezele Ds si Dt care contin cele doua puncte. Daca
acestea nu se afla in acelasi trapez, sa presupunem ca vs si vt nodurile din graf care au
fost plasate in centrele celor doua trapeze. Drumul dintre vs si vt pe care il construim se
compune din trei parti: prima parte este un segment de dreapta
de la ps la vs, a doua parte este un drum
de la vs la vt, si a treia parte
este un segment de dreapta de la vt
la pt.
Un drum intre doua virfuri
poate fi determinat cu ajutorul algoritmului lui Dijkstra.
In a doua
etapa presupunem ca robotul R
este un disc de raza r cu
centrul aflat in ps,
si trebuie sa ajunga cu centrul in pt fara sa penetreze vreun obstacol. Am
precizat mai sus ca unii roboti au limitari destul de severe in
ceea ce priveste libertatea de miscare. Pentru simplificare vom
considera ca discul acopera in intregime robotul.
Ca si pina
acum, obstacolele sint poligoane disjuncte. Problema robotului discoidal poate
fi adusa la problema precedenta astfel. Intr-o prima faza,
de preprocesare, se inconjura fiecare poligon cu o banda de
latime egala cu r
(raza discului), care este chiar urma pe care ar lasa-o discul
deplasindu-se de-a lungul frontierei poligonului (a se vedea figura 4.??).
Se impune o
observatie: prin extinderea obstacolelor este posibil ca din doua
obstacole sa se obtina unul singur, atunci cind doua noi
obstacole nu mai sint disjuncte.
In faza a
doua fiecare obstacol nou construit se ajusteaza pentru virfurile convexe,
inlocuindu-se arcele de cerc cu segmente tangente la aceste arce.
In continuare
robotul poate fi redus la un punct si se poate astfel determina un drum
intre cele doua virfuri s
si t.






