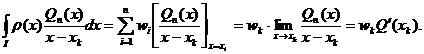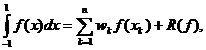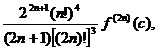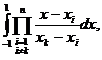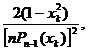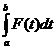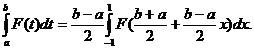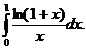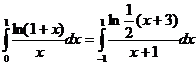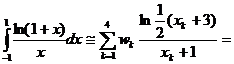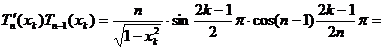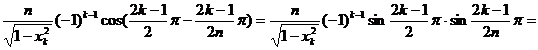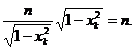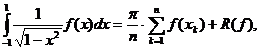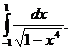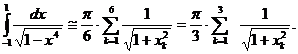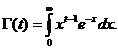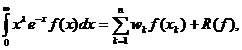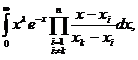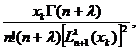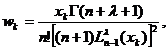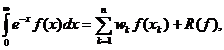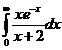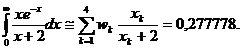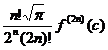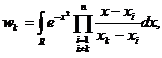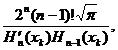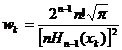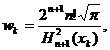Formulele Gauss
Formulele
de integrare numerica de tip Gauss se folosesc in special pentru
aproximarea integralelor improprii. Forma generala a acestor formule este:
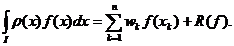
unde I este un interval real, finit
sau infinit, 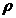 :I
:I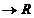 este o funcție pozitiva și continua, astfel incat
este o funcție pozitiva și continua, astfel incat 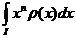 exista pentru orice n
exista pentru orice n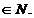 Numerele w
Numerele w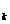 ,x
,x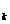
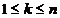 , se determina astfel incat formula (75) sa fie exacta
pentru polinoame de grad mai mic sau egal cu 2n-1. Pentru deducerea acestor
formule se folosesc polinoamele ortogonale.
, se determina astfel incat formula (75) sa fie exacta
pentru polinoame de grad mai mic sau egal cu 2n-1. Pentru deducerea acestor
formule se folosesc polinoamele ortogonale.
Voi
prezenta in continuare metoda generala pentru obținerea acestor
formule și apoi cateva formule particulare.
Fie
f:I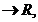 f
f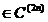 (I), pentru care exista integrala
(I), pentru care exista integrala
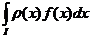 , și
, și 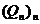 un șir de polinoame definite pe
intervalul real I, ortogonale in raport cu ponderea
un șir de polinoame definite pe
intervalul real I, ortogonale in raport cu ponderea 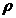
Consideram
in I punctele distincte x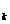
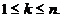 Formula de interpolare a lui
Lagrange pentru funcția f pe aceste noduri este: f(x)=p(x)+r(x),
Formula de interpolare a lui
Lagrange pentru funcția f pe aceste noduri este: f(x)=p(x)+r(x),
unde:
p(x)=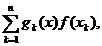 g
g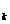 (x)=
(x)=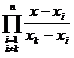 ,
,
r(x)=
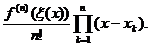
Vom avea:
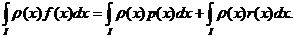
Rezulta:
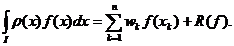
unde:
w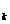 =
=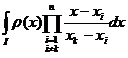 ,
, 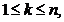

R(f)=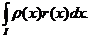
Vom determina nodurile x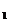 ,x
,x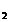 ,,x
,,x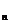 astfel incat R(f)=0 pentru f polinom de grad cel mult 2n-1.
In acest caz
astfel incat R(f)=0 pentru f polinom de grad cel mult 2n-1.
In acest caz 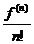 este polinom de grad
cel mult n-1, iar
este polinom de grad
cel mult n-1, iar 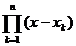 este polinom de grad
n. Cum
este polinom de grad
n. Cum 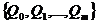 determina o
baza in spațiul vectorial al polinoamelor de grad cel mult m,
rezulta:
determina o
baza in spațiul vectorial al polinoamelor de grad cel mult m,
rezulta:
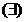
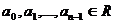 a.i.
a.i. 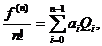
(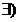 b
b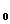 ,
,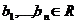 a.i.
a.i. 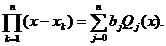
Obținem:
R(f)= 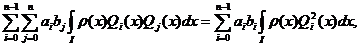
pentru ca 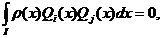 daca
daca 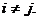
Pentru 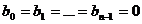 rezulta R(f)=0. In acest caz:
rezulta R(f)=0. In acest caz:
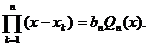
Deci, 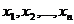 sunt radacinile
polinomului
sunt radacinile
polinomului 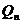 , iar
, iar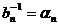 , unde
, unde 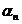 este coeficientul dominant al
aceluiaș polinom.
este coeficientul dominant al
aceluiaș polinom.
Fie acum
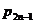 polinomul de interpolare Hermite de
grad cel mult 2n-1 cu proprietațile:
polinomul de interpolare Hermite de
grad cel mult 2n-1 cu proprietațile:
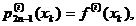
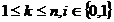
Deci:
f=p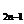 +r
+r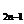 , unde : r
, unde : r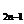 (x)=
(x)=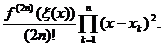
Avem:
R(f)=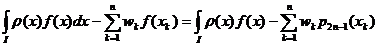
Cum formula (75) este exacta pentru p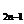 , rezulta:
, rezulta:
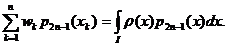
Deci:
R(f)=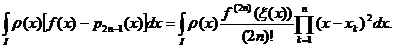
Aplicand
o teorema de medie pentru ultima integrala, rezulta
existența unui punct c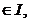 astfel incat:
astfel incat:
R(f)=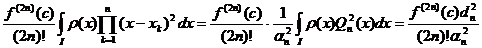
unde: d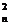
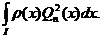
Deci,
forma generala a formulelor de tip Gauss este:
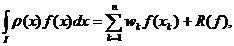 unde:
unde:
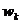
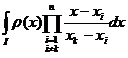
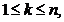
R(f)=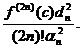
In
aceste formule 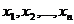 sunt radacinile
polinomului
sunt radacinile
polinomului 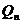 dintr-un șir de polinoame (
dintr-un șir de polinoame (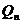
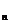 , ortogonale in I in raport cu
, ortogonale in I in raport cu 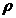
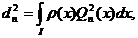 iar
iar 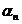 este coeficientul dominant din
expresia polinomului
este coeficientul dominant din
expresia polinomului 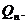
In
formulele (80), pentru calculul numerelor 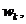 intervin din nou integrale pe
intervalul I. Pentru calculul acestor numere vom deduce formule mai simple, in
care intervin valorile polinoamelor
intervin din nou integrale pe
intervalul I. Pentru calculul acestor numere vom deduce formule mai simple, in
care intervin valorile polinoamelor 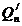 și
și 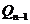 in x
in x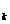 . Pentru aceasta vom utiliza formula Cristoffel-Darboux :
. Pentru aceasta vom utiliza formula Cristoffel-Darboux :
(x-y)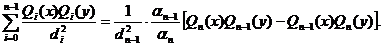
Pentru
y=x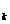 , unde
, unde 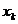 este o radacina a
polinomului
este o radacina a
polinomului 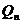 , vom avea:
, vom avea:
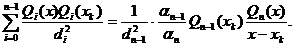
Rezulta:
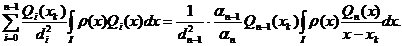
Dar:
 pentru
pentru 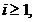
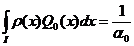
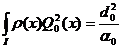 , (
, (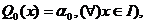
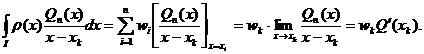
Revenind in (82) obținem:
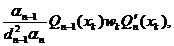
de unde :
w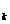 =
=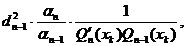
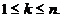
In continuare vom deduce patru formule de tip Gauss,
corespunzatoare polinoamelor ortogonale
1. Formula Gauss-Legendre.
Polinoamele lui Legendre:
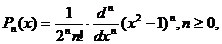
sunt
definite pe I=(-1,1) și sunt ortogonale in raport cu ponderea 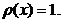 Pentru aceste
polinoame avem:
Pentru aceste
polinoame avem:
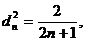
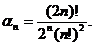
Formula Gauss-Legendre, dedusa
din (79)-(80)-(81), este:
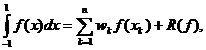
unde:
R(f)=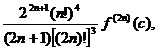 c
c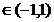
w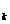
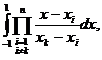
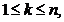
sau, dupa (83):
w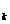 =
=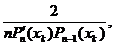
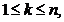
In aceste formule 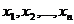 sunt radacinile
polinomului p
sunt radacinile
polinomului p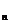
Comentarii. 1 Utilizand formula de
recurența:
Utilizand formula de
recurența:
(1-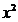 )
)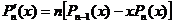 ,
, 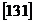
și
formula (87) obținem:
w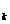 =
=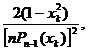
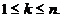
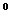 Pentru o integrala de forma
Pentru o integrala de forma 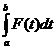 se efectueaza schimbarea de
variabila:
se efectueaza schimbarea de
variabila:
t=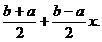
Rezulta:
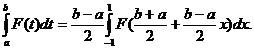
Pentru ultima integrala se
aplica formula (84) cu:
f(x)=F(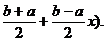
Exemplu. Fie I=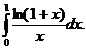
Avem:
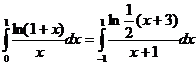
Pentru n=4 avem:

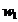
x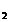
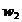
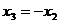
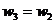
x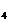
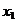
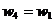
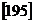
Rezulta: 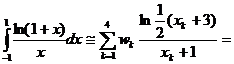
2. Formula
Gauss-Cebișev.
Polinoamele lui
Cebișev:
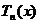 = cos(n* arccos x), n
= cos(n* arccos x), n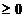 ,
,
sunt definite pe intervalul I=(-1,1) și
ortogonale in raport cu ponderea : 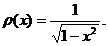
In acest caz avem: 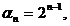 d
d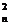
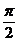 pentru
pentru 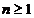 și d
și d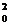
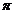
Radacinile
polinomului 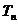 sunt
sunt 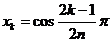 ,
, 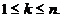
Avem:
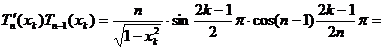
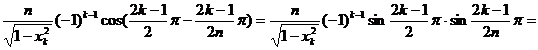
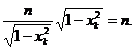
Utilizand formula (83) obținem:
w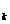 =
=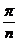 ,
, 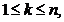 (n
(n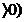
Formula Gauss-Cebișev este:
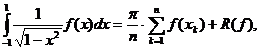
unde:
x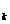 =cos
=cos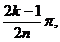
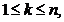
R(f)= 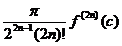 , c
, c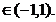
Pentru integrale de forma 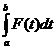 se efectueaza schimbarea de
variabila t=
se efectueaza schimbarea de
variabila t=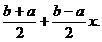
Rezulta:
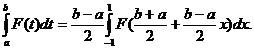
Pentru a doua integrala din aceasta egalitate se
aplica formula (90) cu f(x)=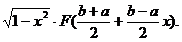
Exemplu. Fie I=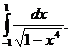
Aplicam formula (90) cu f(x)= 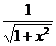 și n=6. Avem:
și n=6. Avem:
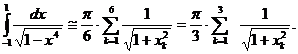
Ultima egalitate are loc pentru ca:
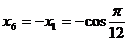
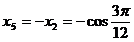
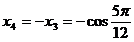
Se obține: I
3 Formula Gauss-Laguerre.
Polinoamele lui Laguerre:
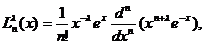
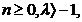
sunt definite pe intervalul I=(0,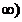 și ortogonale in raport cu ponderea
și ortogonale in raport cu ponderea 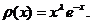 Pentru aceste polinoame avem:
Pentru aceste polinoame avem:
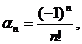 d
d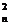
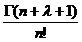 , unde
, unde 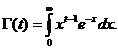
Formula Gauss-Laguerre este:
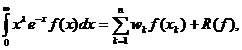
unde:
w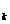 =
=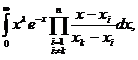
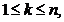
R(f)=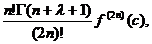 c
c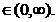
Folosind
formula (83) obținem:
w =-
=-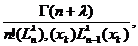
In aceste formule 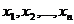 sunt radacinile
polinomului
sunt radacinile
polinomului 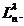
Comentarii. 1 . Utilizand formula:
. Utilizand formula:
X(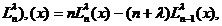
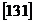 ,
,
obținem:
w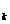 =
=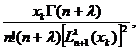
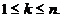
Daca in plus, folosim și
formula de recurența:
(n+1)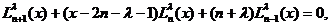
Atunci (97) devine:
(98) 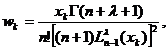
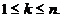
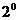 Pentru
Pentru 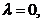 deoarece
deoarece 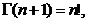 se obține formula:
se obține formula:
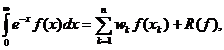
unde:
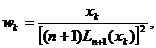
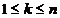 ,
,
R(f)=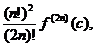 c
c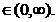
(Am notat
cu 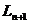 polinomul
polinomul 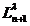 pentru
pentru 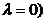 .
.
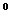 Pentru integrale de forma
Pentru integrale de forma 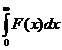 se folosește formula (93) cu
f(x)=
se folosește formula (93) cu
f(x)= 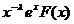 , sau formula (99) cu f(x)=
, sau formula (99) cu f(x)=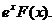
Exemplu. Pentru integrala 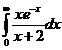 vom aplica formula (99) cu f(x)=
vom aplica formula (99) cu f(x)=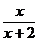 și n=4.
și n=4.
In acest caz avem:
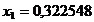
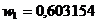
x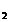
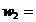
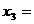 4,536620
4,536620 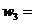 0,038888
0,038888
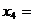 9,395071
9,395071 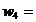 0,000539
0,000539 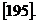
Rezulta:
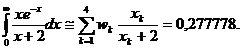
4. Formula
Gauss-Hermite.
Polinoamele
lui Hermite:
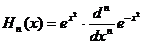 ,
, 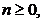
definite
pe R, sunt ortogonale in raport cu ponderea 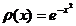 .
.
In acest caz: 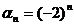 ,
, 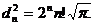
Formula
Gauss-Hermite este:
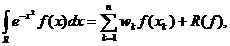
R(f)=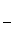
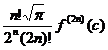 , c
, c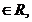
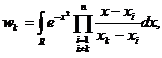
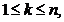
sau :
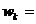
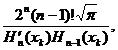
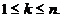
In aceste formule 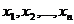 sunt radacinile
polinomului
sunt radacinile
polinomului 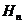
Comentarii. 1 Folosind formula de recurența:
Folosind formula de recurența:
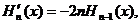
din (105) rezulta:
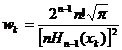
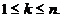
Daca se adauga și formula de
recurența:
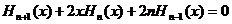
Atunci (106) devine:
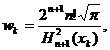
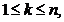
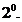 Pentru integrale
de forma
Pentru integrale
de forma 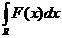 se folosește formula
(102) cu f(x)=
se folosește formula
(102) cu f(x)=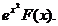
Exemplu. Pentru 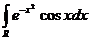 in (102) vom lua f(x)=cosx.
in (102) vom lua f(x)=cosx.
Pentru n=5 avem:
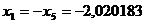
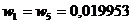
x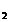
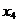
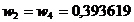
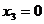
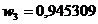
Se
obține:
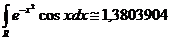
Valoarea
exacta a integralei este 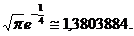


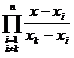 ,
, 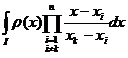 ,
,