Erori
de-ale matematicienilor
Pot gresi matematicienii in
calculele si demonstratiile lor? Cum sa nu!
Dreptul la greseala neintentionata este cel
dintai din toate drepturile, nu numai in viata omeneasca (ca nu e om
care sa vietuiasca si sa nu greseasca), ci si in domeniul
stiintelor. Si cei mai ilustrii s-au inselat. Au spus
strabunii nostrii romani: Errare humanum est, perseverare diabolicum .
Sa luam numai prima parte a maximei: 'A gresi este
omeneste'; a gresi insa neintentionat.
De unde provin greselile
neintentionate in stiinte in general si in matematica in cazul special
ce-l discutam? Erorile provin din lipsa de atentie la calcule sau demonstratii,
din graba de a publica, din distractie, din erori de tipar, din
neperfectionarea simturilor noastre care pot duce la iluzii optice in cazul
geometriei, sau din nestiinta.
Cel dintai care s-a gandit sa adune intr-un volum erori ale matematicienilor a
fost spaniolul Luciano Novarroin 1886. Ulterior, in revista l'Intermédiare
des mathématiciens ,
in rastimpul anilor s-au adunat multe erori de asemenea natura. In
sfarsit, o carte interesanta publicata in acest domeniu este cea a lui Maurice Lecat: Erreurs de mathématiciens
des origines a nos jours (Erori ale matematicienilor de la origini
pana in zilele noastre), tiparita la Bruxelles si Louvain in 1935.
Exista in lume un singur matematician care nu are nici o eroare: Galois.
Dar este explicabil: a murit la 21 de ani si
toata opera lui - de mare valoare de altfel - insumeaza 60 de pagini.
De aceea Galois are, cum spune belgianul Maurice Lecat, casier vierge (cazierul
nepatat). Daca ar fi trait mai mult, probabil
nici Galois nu ar fi fost scutit de greseala.
Dintre genille
matematice au comis erori si Gauss, si Newton. Nu putem spune nimic de Arhimede
deoarece nu a lasat nimic scris de mana sa, adica, mai bine zis,
pana la descoperirea documentului de la Constantinopol (azi Istanbul),
gasit in 1906 de catre J.L. Heinberg si intitulat Teoreme de
mecanica, metode , tratat adresat de Arhimede prietenului sau
Eratostene, nu cunosteam nimic scris de Arhimede; totul ne fusese transmis prin
altii. Dar acest tratat gasit la Constantinopol nu a
fost studiat din punct de vedere al eventualelor erori.
Dintre marii matematicieni au
comis importante erori: Abel, Chauchy, Descartes, Euler, Fermat, Hermite,
Jacobi, Lagrange, Laplace, Leibniz, Pointcaré,
Sylvester. Dintre ceilalti
matematicieni care au erori de calcul sau demonstratii putem cita
pe Michel Chasles, Legendre, iar dintre fizico-matematicieni pe Galileo Galilei.
Legendre a dat, de exemplu, 7 demonstratii, toate bineinteles
eronate, pentru postulatul al V-lea a lui Euclid rpivind dreptele paralele.
Fizicianul Ampere a gasit - dar scuzabil, deoarece era in varsta de
13 ani - cvadratura cercului .
Sonia Kowalewski a avut si ea erori de demonstratie intr-una din lucrarile
sale importante, erori care au fost aratate in detaliu de matematicianul italian Vito Volterra.
Altii au comis
erori cu privire la misticismul numerelor. Dar, lasand la o parte erorile privind problemele
nerezolvabile din matematica, aici este vorba
de erori importante de calcul sau demonstratie de ale matematicienilor. De ce sa fie scutiti matematicienii de asemenea erori?
Este admisibil ca Euler, a carui opera cuprinde deocamdata 72 de
volume, sa nu aiba nici o eroare intr-o
opera atat de vasta? Este imposibil ca lui Henri Pointcaré ultimul
savant universal, care de obicei nu-si revizuia manuscrisele ci le da la tipar
asa cum ieseau din prima redactare, este imposibil, spuneam, sa nu i se
gaseasca vreo eroare in vasta sa opera cuprinzand peste 500 de
memorii si peste 30 de volume tiparite.
Cele mai multe
erori ale matematicienilor sunt din domeniul teoriei numerelor. Asa, de exemplu, Euler a
calculat numerele prime de forma 232a 2 + 1 si a dat 76 de valori. Printre cele 76 de valori doua sunt gresite. Si anume Euler a socotit numere prime pe 232 x 57 2 + 1 si 232 x
117 2 + 1. Dar acestea nu sunt numere prime pentru ca s-a dovedit
ulterior ca 232 x 57 2 + 1 = 179 x 4 211 iar 232 x 117 2 + 1 = 271 x 11
719.
Tot Euler a socotit numarul
1 000 169 ca fiind prim, cand in realitate el este
egal cu 197 x 5 077. La fel a spus ca 1234 2 + 1 este
prim, cand realmente este egal cu 421 x 3 617. Abatele Mersenne considera pe 2
61 - 1 ca numar neprim, desi in realitate acesta este
prim. Iar Leibniz a scris ca 2 n - 2 nu se divide cu n decat daca n
este prim, eroare pe care a indreptat-o el insusi mai tarziu. Si fiindca
veni vorba de numere prime sa consemnam aici
ca cel mai mare numar prim cunoscut este 2 4423 - 1.
Lagrange a
afirmat ca orice numa este diferenta a doua patrate,
ceea ce nu are loc intotdeauna. Gauss a spus ca restul diviziunii lui 20 4
prin 113 este 2, ceea ce nu-i just. Newton a afirmat ca nici o ovala nu
se poate rectifica si nici nu i se poate face cvadratura, ceea ce nu-i adevarat. Cat priveste pe
Descartes, acesta a dat o relatie inexacta intre spatiu si timp in
caderea corpurilor. Asa ca nu numai filozoful
antichitatii Aristotel a gresit esential spunand ca 'un corp de
2 ori mai greu cade de 2 ori mai repede', ci a gresit insusi Descartes.
D'Alembert, Laplace si Poisson au facut
erori de calcule in calculul probabilitatilor .
Am putea prelungi mult citarea de
erori de-ale matematicienilor. S-au scris cum spuneam, in
aceasta privinta cele 2 volume ale lui Novarro si Maurice Lecat.
Ne oprim aici insa numai cu cateva erori citate, fiindca chiar in
acestea puteti vedea ca nici un domeniu matematic
nu este scutit de erori involuntare.
Erori de istorie matematica
Dar in afara de erori
neintetionate de-ale matematicienilor sunt si erori de istorie matematica,
fiindca adevarul istoric privind paternitatea anumitor
descoperiri matematici nu s-a putut stabili intotdeauna cu precizie.
Spunem, de
exemplu, teorema lui Pitagora la teorema din geometrie privind relatia
numerica dintre patratul ipotenuzei si suma catetelor unui triunghi
dreptunghic, cand in realitate aceasta teorema a fost luata de
Pitagora de la babilonieni. Deci ar trebui sa i se spuna teorema babiloneana ;
iata o importanta eroare istorica.
Tot asa, pana in anul 1911
s-a considerat ca Heron cel Batran a stabilit aria triunghiului in
functie de laturi :
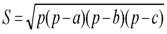 .
Recent s-a dovedit insa ca relatia aceasta o stabilise anterior
Arhimede. Se atribuie apoi in toate cartile de matematica lui Euler
paternitatea relatiei care leaga distanta dintre centrele cercului
circumscris si celui inscris intr-un triunghi de razele acestor cercuri ,
relatie care se numeste a lui Euler .In realitate, aceasta a fost
descoperita de William Chapple in 1746 si publicata in revista Miscellanea
curiosa mathematica (Diferite curiozitati matematice) care a dat-o sub
forma obisnuita in care o intalnim astazi: d 2 = R (R - 2r), pe cand
Euler a dat-o intr-o forma neutilizata astazi.
.
Recent s-a dovedit insa ca relatia aceasta o stabilise anterior
Arhimede. Se atribuie apoi in toate cartile de matematica lui Euler
paternitatea relatiei care leaga distanta dintre centrele cercului
circumscris si celui inscris intr-un triunghi de razele acestor cercuri ,
relatie care se numeste a lui Euler .In realitate, aceasta a fost
descoperita de William Chapple in 1746 si publicata in revista Miscellanea
curiosa mathematica (Diferite curiozitati matematice) care a dat-o sub
forma obisnuita in care o intalnim astazi: d 2 = R (R - 2r), pe cand
Euler a dat-o intr-o forma neutilizata astazi.
La fel spunem, in geometria triunghiului , teorema
privind dreapta lui Simsom , cand este in realitate datorita lui William
Wallace, care a publicat-o in 1800. Corect ar trebui sa spunem deci dreapta
lui Wallace .

