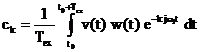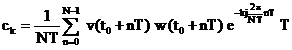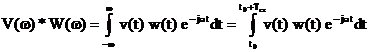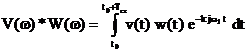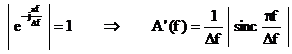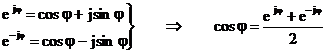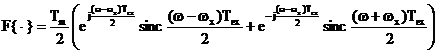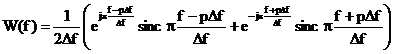v
Analiza semnalelor cu ajutorul
transformatei Fourier discrete
v
Curent se folosesc urmatorii
termini: Transformata Fourier Discreta (DFT = Discrete Fourier Transform)
care este metoda matematica prin care se studiaza spectrul semnalelor
esantionate si Transformata Fourier Rapida (FFT = Fast Fourier
Transform), este acea varianta a metodei DFT in care s-au minimizat
numarul operatiilor aritmetice. FFT este de fapt algoritmul prin care
se implementeaza DFT.
Analiza in frecventa a
semnalelor analitice
v
Rezultatul
transformatei Fourier discrete este un spectru de linii obtinut cu formula
de calcul a coeficientilor seriei Fourier sau se calculeaza prin
esantionarea in frecventa a unei functii de densitate
spectrala rezultata din transformata Fourier. Din aceste motive,
in interpretarea rezultatului transformatei Fourier discrete intervin atat
proprietatile seriei Fourier cat si ale transformatei Fourier.
In acest subcapitol se reiau succint acele proprietati ale seriei
Fourier complexe si ale transformatei Fourier care ulterior vor fi
folosite pentru demonstrarea proprietatilor transformatei Fourier
discrete.
Seria Fourier complexa
v
Seria
Fourier se foloseste pentru analiza semnalelor periodice. Un semnal 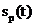 este periodic
daca pentru orice valoare a variabilei independente
este periodic
daca pentru orice valoare a variabilei independente 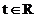 exista cel
putin un numar constant
exista cel
putin un numar constant 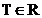 numit perioada a
semnalului pentru care este valabila afirmatia:
numit perioada a
semnalului pentru care este valabila afirmatia:
v
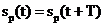 . (2.1)
. (2.1)
v
Valoarea
minima a numarului 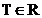 se noteaza
se noteaza 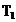 si se
numeste perioada principala a semnalului, iar
si se
numeste perioada principala a semnalului, iar 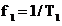 frecventa fundamentala
a semnalului. Perioada principala a semnalului are proprietatea:
frecventa fundamentala
a semnalului. Perioada principala a semnalului are proprietatea:
v
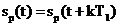 ,
, 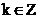 . (2.2)
. (2.2)
v
Frecventele
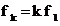 sunt armonicele semnalului
periodic, iar pentru
sunt armonicele semnalului
periodic, iar pentru 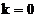 ,
, 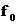 este componenta
continua a semnalului. Semnalul
este componenta
continua a semnalului. Semnalul 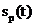 poate fi unic
reprezentat in functie de armonicele sale:
poate fi unic
reprezentat in functie de armonicele sale:
v
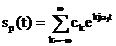 , (2.3)
, (2.3)
v
unde
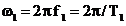 este frecventa
semnalului
este frecventa
semnalului 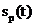 masurata in
masurata in 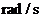 , iar
, iar 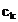 , sunt coeficientii Fourier complecsi
calculati cu formula:
, sunt coeficientii Fourier complecsi
calculati cu formula:
v
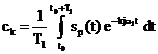 . (2.4)
. (2.4)
v
Analiza
pe o perioada a semnalului 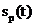 descrie complet
comportarea semnalului pentru
descrie complet
comportarea semnalului pentru 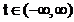 . Rezultatul analizei nu depinde de momentul initial
. Rezultatul analizei nu depinde de momentul initial 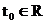 care in (2.4) este o constanta arbitrara.
care in (2.4) este o constanta arbitrara.
v
Seria
Fourier da un spectru de linii compus dintr‑o componenta
continua, amplitudinea si faza fundamentalei spectrului si
amplitudinea si faza armonicelor. Din coeficientul complex 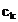 se calculeaza
amplitudinea
se calculeaza
amplitudinea 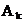 si faza
si faza 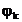 a liniei spectrale de
ordinul k:
a liniei spectrale de
ordinul k:
v
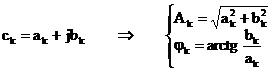 . (2.5)
. (2.5)
v
Pe
o axa continua spectrul de amplitudine al semnalului periodic 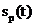 (2.5), se reprezinta
sub forma unei distributii:
(2.5), se reprezinta
sub forma unei distributii:
v
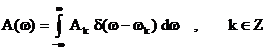 , (2.6)
, (2.6)
v
unde:
v
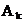 este amplitudinea
liniei spectrale;
este amplitudinea
liniei spectrale;
v
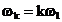 este frecventa
liniei spectrale corespunzatoare armonicii de ordinul k;
este frecventa
liniei spectrale corespunzatoare armonicii de ordinul k;
v
 este frecventa
fundamentala a spectrului;
este frecventa
fundamentala a spectrului;
v
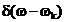 este functia
este functia 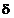 care da forma
liniei spectrale cu frecventa
care da forma
liniei spectrale cu frecventa 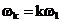 .
.
v Semnalul periodic 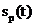 are serie Fourier
daca sunt indeplinite conditiile Dirichlet. Prima conditie
Dirichlet cere ca integrala:
are serie Fourier
daca sunt indeplinite conditiile Dirichlet. Prima conditie
Dirichlet cere ca integrala:
v
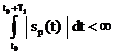 (2.7)
(2.7)
v
sa
fie convergenta. A doua conditie Dirichlet cere ca semnalul 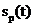 sa aiba un
numar finit de intervale de monotonie in intervalul
sa aiba un
numar finit de intervale de monotonie in intervalul 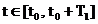 .
.
Transformata Fourier
v
Transformata
Fourier se foloseste pentru analiza semnalelor aperiodice (numite si
impulsuri). Semnalele aperiodice nu au o frecventa
fundamentala, ci contin intr‑o masura mai mica
sau mai mare toate frecventele in domeniul 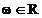 . Fie semnalul aperiodic
. Fie semnalul aperiodic 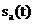 . Spectrul semnalului
este o functie continua de densitate spectrala
. Spectrul semnalului
este o functie continua de densitate spectrala 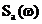 ,
, 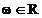 . Similar ca in (2.3) sau (2.6) semnalul
. Similar ca in (2.3) sau (2.6) semnalul 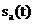 poate fi unic
reprezentat in functie de functia sa de densitate spectrala:
poate fi unic
reprezentat in functie de functia sa de densitate spectrala:
v
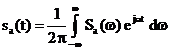 . (2.8)
. (2.8)
v
Functia
de densitate spectrala a semnalului aperiodic 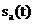 este:
este:
v
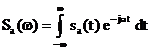 , (2.9)
, (2.9)
v
Spectrele
de amplitudine si faza sunt:
v
 (2.10)
(2.10)
v
unde
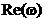 ,
, 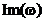 ,
, 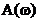 si
si 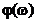 sunt functii
sunt functii 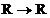 , continue pentru
, continue pentru 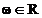 . Semnalul aperiodic
. Semnalul aperiodic 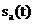 are transformata
Fourier daca sunt indeplinite conditiile lui Dirichlet. In acest caz,
prima conditie a lui Dirichlet cere ca integrala
are transformata
Fourier daca sunt indeplinite conditiile lui Dirichlet. In acest caz,
prima conditie a lui Dirichlet cere ca integrala
v
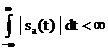 (2.11)
(2.11)
v
sa
fie convergenta, iar a doua conditie Dirichlet cere ca semnalul 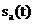 sa aiba un
numar finit de intervale de monotonie pentru
sa aiba un
numar finit de intervale de monotonie pentru 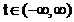 .
.
Diferenta dintre seria
Fourier si transformata Fourier
v
Diferentele
dintre seria Fourier si transformata Fourier pot fi explicate pe exemple
simple. Fie semnalul armonic
v
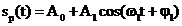 , (2.12)
, (2.12)
v
unde
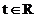 , iar
, iar 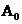 ,
, 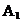 ,
,  si
si 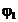 sunt numere reale
fixate. Pentru acest semnal sunt indeplinite ambele conditii ale lui
Dirichlet formulate pentru seria Fourier, integrala (2.7) este finita
si intr‑o perioada sunt un numar finit de intervale de
monotonie. In acelasi timp, conditiile lui Dirichlet formulate pentru
transformata Fourier nu sunt indeplinite. Daca
sunt numere reale
fixate. Pentru acest semnal sunt indeplinite ambele conditii ale lui
Dirichlet formulate pentru seria Fourier, integrala (2.7) este finita
si intr‑o perioada sunt un numar finit de intervale de
monotonie. In acelasi timp, conditiile lui Dirichlet formulate pentru
transformata Fourier nu sunt indeplinite. Daca 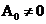 atunci prima
conditie a lui Dirichlet (2.11) nu este indeplinita si nici nu
se poate vorbi despre un numar finit de intervale de monotonie pentru
atunci prima
conditie a lui Dirichlet (2.11) nu este indeplinita si nici nu
se poate vorbi despre un numar finit de intervale de monotonie pentru 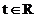 .
.
v
Similar,
pentru semnalele aperiodice nu este valabila conditia de
periodicitate (2.1), deci prima conditie a lui Dirichlet (2.7),
enuntata pentru semnale periodice nu poate fi aplicata
semnalelor aperiodice.
v
Conditiile
lui Dirichlet au formulari diferite atat in cazul seriei Fourier cat
si a transformatei Fourier. Nici semnalele periodice nu au transformate
Fourier si nici semnalele aperiodice nu au serie Fourier.
Alterarea semnalului prin
trunchiere in timp
v
Atat seria Fourier cat si
transformata Fourier sunt metode analitice de prelucrare a semnalelor, deci
semnalele 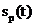 si
si 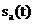 , analizate in subcapitolul 2.1 sunt:
functii algebrice simple, o suma finita de functii algebrice
simple sau functii algebrice simple definite pe un numar finit de
intervale.
, analizate in subcapitolul 2.1 sunt:
functii algebrice simple, o suma finita de functii algebrice
simple sau functii algebrice simple definite pe un numar finit de
intervale.
v
Un semnal analogic,  , prelevat dintr-un circuit de
masura nu este o functie analitica. Acest semnal are
amplitudinea si banda de frecventa limitate si are o desfasurare
infinita in timp. In consecinta si secventa
rezultata din procesul de achizitie a datelor are o
desfasurare infinita in timp. Prin firea lucrurilor, un
calculator numeric nu poate prelucra decat secvente finite de esantioane
ale semnalului
, prelevat dintr-un circuit de
masura nu este o functie analitica. Acest semnal are
amplitudinea si banda de frecventa limitate si are o desfasurare
infinita in timp. In consecinta si secventa
rezultata din procesul de achizitie a datelor are o
desfasurare infinita in timp. Prin firea lucrurilor, un
calculator numeric nu poate prelucra decat secvente finite de esantioane
ale semnalului 
v
Obiectivul acestui subcapitol este
studiul cantitativ al alterarii spectrului semnalului datorata
trunchierii in timp.
Achizitia datelor
v
Achizitia unui semnal este o
succesiune de patru operatii: esantionarea, conversia analog‑numerica
(cuantizarea), scalarea (reprezentarea esantioanelor prin numere reale exprimate
in unitatea de masura a marimii fizice modelate numeric)
si trunchierea in timp.
v
In continuare se considera
un semnal de tensiune  care a fost corect
esantionat (v. teorema lui Shanon), iar conversia
numerica a semnalului
care a fost corect
esantionat (v. teorema lui Shanon), iar conversia
numerica a semnalului  se
face cu un numar suficient de mare de biti. In urma scalarii
secventa rezultata din achizitia datelor este memorata intr‑un
vector de numere reale reprezentate in virgula flotanta.
se
face cu un numar suficient de mare de biti. In urma scalarii
secventa rezultata din achizitia datelor este memorata intr‑un
vector de numere reale reprezentate in virgula flotanta.
v 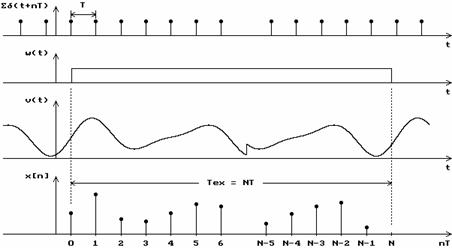
v Figura 2.1. Achizitia semnalului 
v
In figura 2.1 se prezinta
diagrama de timp a functiei delta periodice 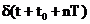 , a functiei fereastra
, a functiei fereastra 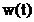 , a semnalului analizat
, a semnalului analizat  si a secventei
si a secventei 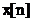 ,
, 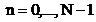 rezultate in urma
achizitiei datelor, unde
rezultate in urma
achizitiei datelor, unde 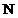 este numarul de
esantioane prelevate din semnalul
este numarul de
esantioane prelevate din semnalul  . In figura s‑au notat
. In figura s‑au notat 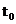 momentul inceperii
achizitiei datelor si
momentul inceperii
achizitiei datelor si 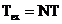 timpul de observare al
semnalului
timpul de observare al
semnalului  ( sau durata
experimentului).
( sau durata
experimentului).
v
Esantionarea se modeleaza matematic prin inmultirea semnalului  cu functia delta
periodica
cu functia delta
periodica 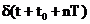 , unde
, unde 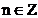 , iar
, iar 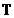 este perioada de
esantionare.
este perioada de
esantionare.
v
Trunchierea in timp se modeleaza prin inmultirea semnalului  cu functia
fereastra
cu functia
fereastra 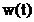 . Functia fereastra are expresia:
. Functia fereastra are expresia:
v
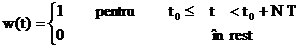 (2.13)
(2.13)
v
In subcapitolul 2.4 se vor studia
si functii fereastra care au forme diferite de (2.13). Aceste
functii trebuie sa se anuleze in afara intervalului 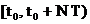 si sa
aiba proprietatea:
si sa
aiba proprietatea:
v
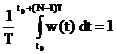 (2.14)
(2.14)
v
Scalarea este operatia inversa a cuantizarii. In urma
scalarii, 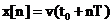 , pentru
, pentru 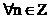 .
.
v
In consecinta procesul
de achizitie a datelor se modeleaza prin:
v
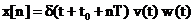 ,
, 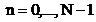 . (2.15)
. (2.15)
Transformata Fourier discreta
v
Transformata Fourier discreta
este o metoda off‑line de prelucrare digitala a semnalelor prin
care dintr‑o secventa 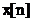 , memorata intr-un vector de dimensiune finita
se obtine un spectru discret
, memorata intr-un vector de dimensiune finita
se obtine un spectru discret
v
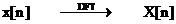 ,
, 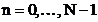 . (2.16)
. (2.16)
v
Secventa 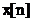 se obtine din
semnalul
se obtine din
semnalul  in urma
esantionarii cu perioada
in urma
esantionarii cu perioada 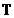 , din care sunt prelevate
, din care sunt prelevate 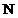 esantioane, indexate
dupa regula
esantioane, indexate
dupa regula 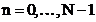 . In figura 2.1 s‑a notat
. In figura 2.1 s‑a notat 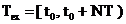 timpul de observare al
semnalului.
timpul de observare al
semnalului.
v
Nu este cunoscuta
evolutia semnalului  pentru
pentru 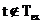 deoarece in afara intervalului
de timp
deoarece in afara intervalului
de timp 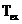 nu s‑a
facut achizitia semnalului analizat. Totusi asupra
evolutiei semnalului
nu s‑a
facut achizitia semnalului analizat. Totusi asupra
evolutiei semnalului  pentru
pentru 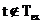 se pot face doua
ipoteze care permit analiza in frecventa a secventei
se pot face doua
ipoteze care permit analiza in frecventa a secventei 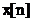 :
:
v
Ipoteza 1. Se presupune ca semnalul  este
periodic cu perioada
este
periodic cu perioada 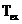 , deci semnalul
, deci semnalul  are serie Fourier
si un spectru discret.
are serie Fourier
si un spectru discret.
v
Ipoteza 2. Se presupune ca semnalul 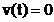 pentru
pentru
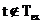 , deci semnalul
, deci semnalul  are transformata
Fourier si un spectru continuu.
are transformata
Fourier si un spectru continuu.
v
Este evident ca ambele
ipoteze ignora forma reala a semnalului  in
afara intervalului de timp in care a fost observat semnalul, dar cele
doua ipotezele sunt necesare pentru a putea aplica una dintre cele
doua metode de analiza in frecventa cunoscute: seria
Fourier sau transformata Fourier.
in
afara intervalului de timp in care a fost observat semnalul, dar cele
doua ipotezele sunt necesare pentru a putea aplica una dintre cele
doua metode de analiza in frecventa cunoscute: seria
Fourier sau transformata Fourier.
Calculul spectrului DFT in
conditiile primei ipoteze
v
Se
considera un semnal armonic  care are si o
componenta continua. Prin inmultire cu functia
fereastra
care are si o
componenta continua. Prin inmultire cu functia
fereastra 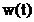 din acest semnal se
"decupeaza" portiunea
din acest semnal se
"decupeaza" portiunea 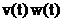 care se periodizeaza
cu perioada
care se periodizeaza
cu perioada 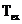 . In cazul primei ipoteze semnalul analizat de transformata
Fourier discreta este:
. In cazul primei ipoteze semnalul analizat de transformata
Fourier discreta este:
v
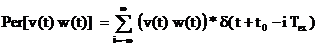 , (2.17)
, (2.17)
v
unde
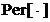 este operatorul de
prelungire periodica a portiunii de semnal
este operatorul de
prelungire periodica a portiunii de semnal 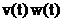 . In membrul drept al functiei (2.17) convolutia
cu functia
. In membrul drept al functiei (2.17) convolutia
cu functia 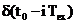 ,
, 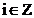 face o translatie
a portiunii de semnal
face o translatie
a portiunii de semnal 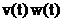 cu intervalul de
timp
cu intervalul de
timp 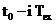 .
.
v
In
figura 2.2 se prezinta semnalul  , functia fereastra
, functia fereastra 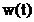 , (v. functia (2.14)), iar in a treia diagrama de
timp, in intervalul
, (v. functia (2.14)), iar in a treia diagrama de
timp, in intervalul 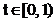 este reprezentat
semnalul
este reprezentat
semnalul 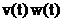 , obtinut in urma procesului de achizitie a
datelor. In figura timpul este reprezentat pe o axa continua,
marcajele sunt in pozitiile
, obtinut in urma procesului de achizitie a
datelor. In figura timpul este reprezentat pe o axa continua,
marcajele sunt in pozitiile 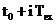 ,
, 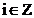 , iar in dreptul marcajului este notat numarul
, iar in dreptul marcajului este notat numarul 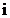 .
.
v 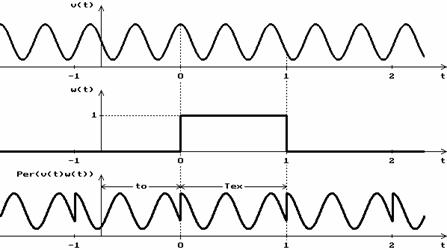
v Figura 2.2. Analiza semnalului  in conditiile
primei ipoteze
in conditiile
primei ipoteze
v
Semnalul
(2.17) este periodic, cu perioada principala 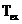 . Din conditiile puse la achizitia semnalului
rezulta ca sunt indeplinite conditiile lui Dirichlet pentru
seria Fourier, deci se poate aplica formula de calcul a coeficientilor
seriei Fourier (2.4)
. Din conditiile puse la achizitia semnalului
rezulta ca sunt indeplinite conditiile lui Dirichlet pentru
seria Fourier, deci se poate aplica formula de calcul a coeficientilor
seriei Fourier (2.4)
v
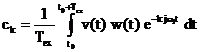 ,
, 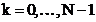 (2.18)
(2.18)
v
unde
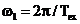 este frecventa
fundamentala a spectrului discret (v. notatiile din sectiunea
2.1). Pentru ca semnalul
este frecventa
fundamentala a spectrului discret (v. notatiile din sectiunea
2.1). Pentru ca semnalul  a fost esantionat
cu perioada
a fost esantionat
cu perioada 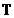 si s‑au
prelevat
si s‑au
prelevat 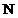 esantioane, in
integrala din formula (2.18) se considera
esantioane, in
integrala din formula (2.18) se considera 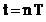 ,
, 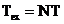 si
si 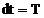 , deci coeficientii
, deci coeficientii 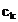 se calculeaza
prin suma:
se calculeaza
prin suma:
v
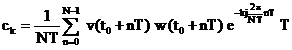 (2.19)
(2.19)
v
In
urma procesului de achizitie a datelor 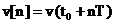 pentru
pentru 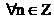 . Daca se esantioneaza si functia fereastra
. Daca se esantioneaza si functia fereastra 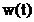 , cu care se face trunchierea in timp, se obtine secventa
, cu care se face trunchierea in timp, se obtine secventa
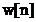 , cu regula de indexare
, cu regula de indexare 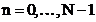 . Cu aceste notatii, dupa simplificari,
formula (2.19) devine
. Cu aceste notatii, dupa simplificari,
formula (2.19) devine
v
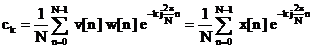 . (2.20)
. (2.20)
v
Formula
(2.20) este foarte importanta pentru ca este folosita de
programul care implementeaza transformata Fourier discreta. Din
(2.13) si din figura 2.2 rezulta ca 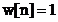 pentru
pentru 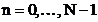 si la prima
vedere, in (2.20) se poate renunta la factorul
si la prima
vedere, in (2.20) se poate renunta la factorul 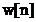 , dar in subcapitolul 2.4 se vor studia si functii
de ponderare,
, dar in subcapitolul 2.4 se vor studia si functii
de ponderare, 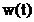 , care au alta forma.
, care au alta forma.
v
In
formula (2.18) frecventa fundamentala a seriei Fourier 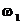 se masoara in
se masoara in 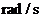 . Traditional, spectrul de linii rezultat din
transformata Fourier discreta se reprezinta pe o axa
liniara sau logaritmica gradata in
. Traditional, spectrul de linii rezultat din
transformata Fourier discreta se reprezinta pe o axa
liniara sau logaritmica gradata in 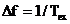 , unde
, unde 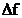 este o unitate de
masura relativa la
este o unitate de
masura relativa la 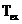 , intervalul de timp in care este observat experimentul.
, intervalul de timp in care este observat experimentul.
v
Marimea
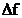 se numeste frecventa fundamentala a spectrului
discret si este intervalul de frecventa minim in care se pot
afla informatii despre semnalul studiat. Din acest motiv,
se numeste frecventa fundamentala a spectrului
discret si este intervalul de frecventa minim in care se pot
afla informatii despre semnalul studiat. Din acest motiv, 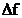 se mai numeste si rezolutia spectrului
discret.
se mai numeste si rezolutia spectrului
discret. 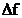 se masoara
in
se masoara
in 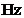 . In (2.20)
. In (2.20) 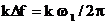 ,
, 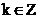 .
.
Proprietati ale
coeficientilor 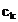
prima
proprietate este 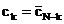 . Din formula lui Euler rezulta ca exponentialele
complexe care intra in calculul coeficientilor
. Din formula lui Euler rezulta ca exponentialele
complexe care intra in calculul coeficientilor 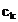 si
si 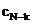 sunt:
sunt:
v
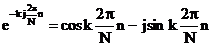 . (2.21)
. (2.21)
v
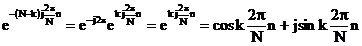 . (2.22)
. (2.22)
v
pentru
ca 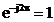 din (2.21), (2.22) si (2.20) rezulta ca
din (2.21), (2.22) si (2.20) rezulta ca 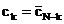 .
.
v
Coeficientii
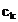 sunt indexati
dupa regula
sunt indexati
dupa regula 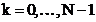 . In consecinta, din proprietatea
enuntata anterior rezulta numarul de coeficienti
independenti:
. In consecinta, din proprietatea
enuntata anterior rezulta numarul de coeficienti
independenti:
v
daca
N este impar atunci 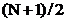 coeficienti
Fourier sunt independenti;
coeficienti
Fourier sunt independenti;
v
daca
N este par atunci 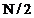 coeficienti
Fourier sunt independenti.
coeficienti
Fourier sunt independenti.
v
Din
sectiunea precedenta rezulta ca 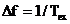 este rezolutia cu
care se calculeaza spectrul secventei
este rezolutia cu
care se calculeaza spectrul secventei 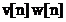 , iar din prima proprietate demonstrata in aceasta
sectiune rezulta ca prelevarea unui numar mai mare de
esantioane in acelasi interval de timp de observare al
experimentului
, iar din prima proprietate demonstrata in aceasta
sectiune rezulta ca prelevarea unui numar mai mare de
esantioane in acelasi interval de timp de observare al
experimentului 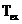 nu
imbunatateste rezolutia spectrului discret, ci
mareste numarul de coeficienti independenti.
nu
imbunatateste rezolutia spectrului discret, ci
mareste numarul de coeficienti independenti.
v
Alte
proprietati importante descriu rolul coeficientilor 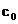 si
si 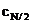 . Coeficientul
. Coeficientul 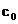 este componenta
continua a semnalului
este componenta
continua a semnalului  pentru ca
pentru ca 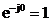 . Daca N este par, exponentiala care
intra in calculul coeficientului
. Daca N este par, exponentiala care
intra in calculul coeficientului 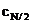 este
este
v
 . (2.23)
. (2.23)
v
Din
(2.23) rezulta ca valoarea coeficientului 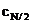 nu depinde de valoarea
componentei continue a semnalului
nu depinde de valoarea
componentei continue a semnalului  pentru ca N este
par. Tot din (2.20) rezulta ca
pentru ca N este
par. Tot din (2.20) rezulta ca 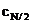 este partea
reala a amplitudinii armonicii cu frecventa egala cu
jumatate din frecventa de esantionare, pe cand partea
imaginara este ignorata. In consecinta, daca
este partea
reala a amplitudinii armonicii cu frecventa egala cu
jumatate din frecventa de esantionare, pe cand partea
imaginara este ignorata. In consecinta, daca 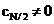 este posibil ca
frecventa de esantionare sa fie prea mica pentru ca in
secventa
este posibil ca
frecventa de esantionare sa fie prea mica pentru ca in
secventa 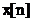 este prezenta o
componenta cu frecventa egala cu jumatate din
frecventa de esantionare.
este prezenta o
componenta cu frecventa egala cu jumatate din
frecventa de esantionare.
Calculul spectrului DFT in
conditiile celei de‑a doua ipoteze
v
Se
considera acelasi semnal  ca in sectiunea
precedenta. In figura 2.3 sunt reprezentate semnalul
ca in sectiunea
precedenta. In figura 2.3 sunt reprezentate semnalul  , functia fereastra
, functia fereastra 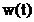 si semnalul
si semnalul 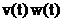 , obtinut in urma procesului de achizitie a
datelor.
, obtinut in urma procesului de achizitie a
datelor.
v 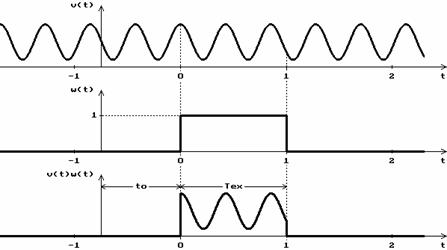
v Figura 2.3. Achizitia semnalului
 in conditiile
celei de‑a doua ipoteze
in conditiile
celei de‑a doua ipoteze
v
Pentru
ca 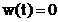 pentru
pentru 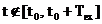 , semnalul
, semnalul 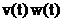 are transformata
Fourier, se aplica formula (2.9) si se obtine functia de
densitate spectrala
are transformata
Fourier, se aplica formula (2.9) si se obtine functia de
densitate spectrala
v
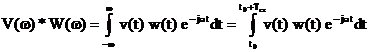 . (2.24)
. (2.24)
v
Se
observa ca formulele (2.18) si (2.24) au aproximativ
aceeasi forma. Daca se fac notatia 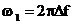 formula (2.18) se pune
sub forma
formula (2.18) se pune
sub forma
v
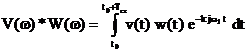 ,
, 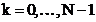 , (2.25)
, (2.25)
v
deci
in formulele (2.24) si (2.25) s-a obtinut aceeasi
integrala. Aparent, cele doua formule sunt echivalente si
coeficientii Fourier complecsi 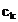 pot fi exprimati
si astfel:
pot fi exprimati
si astfel:
v
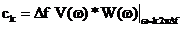 . (2.26)
. (2.26)
v
unde
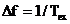 . Formulele (2.24) si (2.26) sunt doar algebric
echivalente pentru ca provin din fenomene fizice diferite. In
sectiunea urmatoare se face o discutie calitativa a relatiei
(2.26).
. Formulele (2.24) si (2.26) sunt doar algebric
echivalente pentru ca provin din fenomene fizice diferite. In
sectiunea urmatoare se face o discutie calitativa a relatiei
(2.26).
Esantionarea in frecventa
a unei functii de densitate spectrala
v
Se
considera un semnal  oarecare si
coeficientii
oarecare si
coeficientii 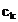 calculati cu
formula (2.20). Amplitudinile armonicilor spectrului discret sunt:
calculati cu
formula (2.20). Amplitudinile armonicilor spectrului discret sunt:
v
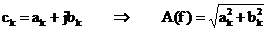 ,
, 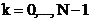 . (2.27)
. (2.27)
v
spectrul
discret 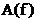 se reprezinta pe o axa continua,
se reprezinta pe o axa continua, 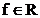 , ca o distributie
, ca o distributie
v
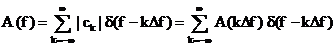 , (2.28)
, (2.28)
v
unde
s‑a notat 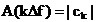 , iar functia
, iar functia 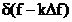 da forma liniei
spectrale. Se observa ca in (2.28) functia delta este
folosita similar ca in (2.15). Din acest motiv, uneori, liniile spectrale
ale spectrului discret sunt numite esantioane de frecventa.
da forma liniei
spectrale. Se observa ca in (2.28) functia delta este
folosita similar ca in (2.15). Din acest motiv, uneori, liniile spectrale
ale spectrului discret sunt numite esantioane de frecventa.
v
Pentru
acelasi semnal  se calculeaza
functia de densitate spectrala
se calculeaza
functia de densitate spectrala 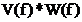 cu formula (2.24)
cu formula (2.24)
v
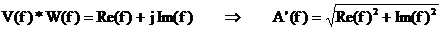 , (2.29)
, (2.29)
v
unde
s‑a notat 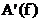 amplitudinea
functiei de densitate spectrala. Daca semnalul experimental
amplitudinea
functiei de densitate spectrala. Daca semnalul experimental  , este o tensiune atunci amplitudinile spectrului discret
, este o tensiune atunci amplitudinile spectrului discret 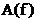 se masoara
in
se masoara
in 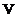 , iar amplitudinea functiei de densitate spectrala
, iar amplitudinea functiei de densitate spectrala 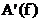 se masoara
in
se masoara
in 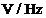 .
.
v
In
figura 2.4 se prezinta 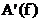 , functia de densitate spectrala de amplitudine a
semnalului
, functia de densitate spectrala de amplitudine a
semnalului  calculata cu
formula (2.29) in conditiile celei de a doua ipoteze si spectrul discret
calculata cu
formula (2.29) in conditiile celei de a doua ipoteze si spectrul discret
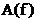 reprezentat sub forma
unei distributii, calculat cu formula (2.28) in conditiile primei
ipoteze.
reprezentat sub forma
unei distributii, calculat cu formula (2.28) in conditiile primei
ipoteze.
v 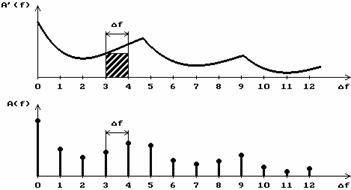
v Figura 2.4. Esantionarea in
frecventa a unei functii de densitate spectrala
v
Se
observa ca pentru 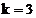 coeficientul
coeficientul 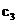 calculat cu
relatia (2.26) este egal cu suprafata
dreptunghiului hasurat. Aceasta inseamna ca relatia (2.26)
este exacta doar daca functia de densitate spectrala
calculat cu
relatia (2.26) este egal cu suprafata
dreptunghiului hasurat. Aceasta inseamna ca relatia (2.26)
este exacta doar daca functia de densitate spectrala 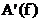 este constanta
in intervalul
este constanta
in intervalul 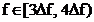 ceea ce in exemplul
prezentat in figura nu se intampla. Relatia (2.26) si
exemplul din figura 2.4 sugereaza ca spectrul discret
ceea ce in exemplul
prezentat in figura nu se intampla. Relatia (2.26) si
exemplul din figura 2.4 sugereaza ca spectrul discret 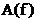 se poate obtine
prin esantionarea in frecventa a functiei de densitate
spectrala
se poate obtine
prin esantionarea in frecventa a functiei de densitate
spectrala 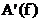 cu pasul de
esantionare
cu pasul de
esantionare 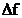 .
.
v
Fenomenul
prin care valoarea functiei de densitate spectrala este
cunoscuta numai in punctele 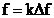 iar in intervalele
iar in intervalele 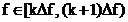 , se pot face doar previziuni ale formei functiei de
densitate spectrala cunoscut prin numele sugestiv Picket Fence Effect.
In figura 2.5 se prezinta
, se pot face doar previziuni ale formei functiei de
densitate spectrala cunoscut prin numele sugestiv Picket Fence Effect.
In figura 2.5 se prezinta 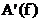 , aceeasi functie de densitate spectrala
folosita in exemplul din figura 2.4. Functia de densitate
spectrala este acoperita de un gard de scanduri prin care se
vad numai punctele
, aceeasi functie de densitate spectrala
folosita in exemplul din figura 2.4. Functia de densitate
spectrala este acoperita de un gard de scanduri prin care se
vad numai punctele 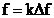 .
.
v 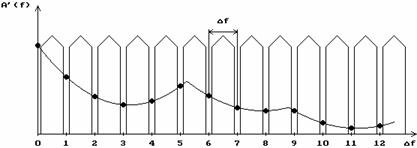
v Figura 2.5. Picket Fence Effect.
v
Din
rezultatele teoretice anterioare se desprind urmatoarele concluzii:
v
nici
una dintre ipotezele enuntate in sectiunea 2.2.2 nu poate fi
verificata, in consecinta formulele (2.20) si (2.25) nu
sunt exacte deci si relatia de echivalenta (2.26) este ea
afectata de erori;
v
formula
(2.20) dedusa din (2.18) (v. sectiunea 2.2.3) este folosita in
practica pentru calculul coeficientilor 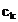 din semnale
esantionate. Din (2.20) nu rezulta nici o informatie despre ce
se intampla intre doua esantioane de frecventa;
din semnale
esantionate. Din (2.20) nu rezulta nici o informatie despre ce
se intampla intre doua esantioane de frecventa;
v
formula
(2.25) este folosita pentru calculul spectrului 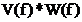 numai din semnale
analitice, nu si din semnale esantionate
numai din semnale
analitice, nu si din semnale esantionate 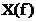 ;
;
v
se
cunoaste forma analitica a functiei fereastra 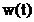 deci se cunoaste
si forma spectrului continuu
deci se cunoaste
si forma spectrului continuu 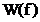 , deci se pot face previziuni analitice ale modului in care
produsul de convolutie
, deci se pot face previziuni analitice ale modului in care
produsul de convolutie 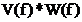 modifica forma
spectrului discret.
modifica forma
spectrului discret.
v
In
subcapitolul 4 sunt studiate formele altor functii fereastra pentru
care se demonstreaza teoretic ca reduc diferentele dintre
formulele (2.20) si (2.26).
Analiza semnalelor armonice cu
transformata Fourier discreta
v
In
acest subcapitol se analizeaza semnale armonice de forma 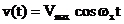 , unde
, unde 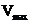 este amplitudinea
semnalului masurata in volti, iar
este amplitudinea
semnalului masurata in volti, iar 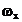 este frecventa
semnalului masurata in
este frecventa
semnalului masurata in 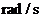 . Din semnal se preleveaza o portiune
continua de durata
. Din semnal se preleveaza o portiune
continua de durata 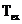 prin inmultire cu
o fereastra rectangulara
prin inmultire cu
o fereastra rectangulara 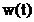 . In sectiunile urmatoare se face un studiu cantitativ
asupra erorilor introduse de trunchierea in timp facuta cu
fereastra rectangulara, asupra estimarii amplitudinii unui
semnal armonic.
. In sectiunile urmatoare se face un studiu cantitativ
asupra erorilor introduse de trunchierea in timp facuta cu
fereastra rectangulara, asupra estimarii amplitudinii unui
semnal armonic.
Spectrul ferestrei rectangulare
v
In
figurile 2.2 si 2.3 pentru trunchierea in timp a semnalului armonic  a fost
facuta cu functia fereastra rectangulara (2.13),
numita si fereastra Dirichlet. Daca se considera
a fost
facuta cu functia fereastra rectangulara (2.13),
numita si fereastra Dirichlet. Daca se considera 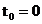 atunci functia
fereastra este
atunci functia
fereastra este
v
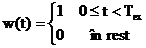 ,
, 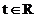 . (2.30)
. (2.30)
v
Functia
fereastra 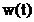 indeplineste
conditiile lui Dirichlet formulate pentru transformata Fourier.
Functia de densitate spectrala corespunzatoare functiei
fereastra (2.30), (v. Adelaida Mateescu, 1975, exemplul de la p.40,) este:
indeplineste
conditiile lui Dirichlet formulate pentru transformata Fourier.
Functia de densitate spectrala corespunzatoare functiei
fereastra (2.30), (v. Adelaida Mateescu, 1975, exemplul de la p.40,) este:
v
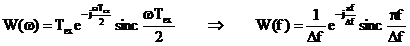 , (2.31)
, (2.31)
v
unde
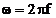 si
si 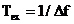 . In literatura, functiile
. In literatura, functiile 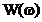 sau
sau 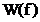 sunt cunoscute sub
numele "nucleul lui Dirichlet".
sunt cunoscute sub
numele "nucleul lui Dirichlet".
v 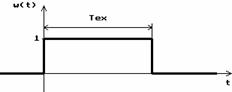
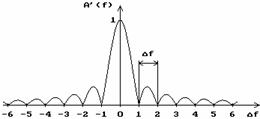
v Figura 2.6. Functiile 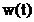 si
si 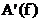 .
.
v
In
figura 2.6 se prezinta forma functiei fereastra
rectangulara 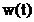 si
si 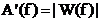 , functia de densitate spectrala de amplitudine. Se
observa ca exponentiala din formula (2.31) nu intra decat
in calculul spectrului de faza pentru ca
, functia de densitate spectrala de amplitudine. Se
observa ca exponentiala din formula (2.31) nu intra decat
in calculul spectrului de faza pentru ca
v
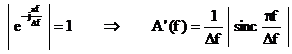 , (2.32)
, (2.32)
v
deci
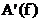 din (2.32) este
expresia analitica a functiei de densitate spectrala de amplitudine
a ferestrei rectangulare
din (2.32) este
expresia analitica a functiei de densitate spectrala de amplitudine
a ferestrei rectangulare
Dificultati teoretice in
analiza DFT a semnalului armonic
v
Semnalul
analizat este 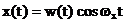 unde
unde 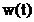 este functia
(2.30). Evident si semnalul
este functia
(2.30). Evident si semnalul 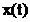 are transformata
Fourier dar functia de densitate spectrala nu se poate pune sub
forma
are transformata
Fourier dar functia de densitate spectrala nu se poate pune sub
forma 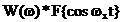 pentru ca
semnalul
pentru ca
semnalul 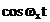 este periodic si
nu indeplineste conditiile lui Dirichlet formulate pentru transformata
Fourier (v. concluziile din sectiunea 2.1.3).
este periodic si
nu indeplineste conditiile lui Dirichlet formulate pentru transformata
Fourier (v. concluziile din sectiunea 2.1.3).
v
Dificultatea
prezentata anterior se depaseste printr‑un artificiu
facut in doi pasi. Intai functia cosinus se exprima cu
ajutorul formulelor lui Euler
v
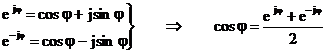 , (2.33)
, (2.33)
v
iar
cu aceasta formula semnalul 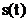 se pune sub forma:
se pune sub forma:
v
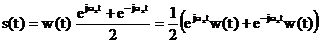 . (2.34)
. (2.34)
v
Apoi
se aplica teorema modularii din transformata Fourier (v. Adelaida
Mateescu, 1975, p.40 si exemplul de la p.41)
v
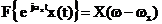 . (2.35)
. (2.35)
v
Din
(2.34) si (2.35) rezulta
v
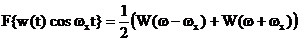 . (2.36)
. (2.36)
v
Notam
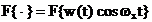 . Inlocuind
. Inlocuind 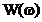 din (2.31) in (2.36),
se obtine
din (2.31) in (2.36),
se obtine
v
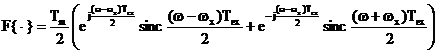 . (2.37)
. (2.37)
v
Se
noteaza 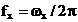 ,
, 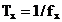 si se
observa ca
si se
observa ca 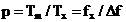 , deci numarul
, deci numarul 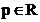 este numarul de
perioade prelevate din semnalul
este numarul de
perioade prelevate din semnalul 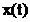 , sau frecventa semnalului
, sau frecventa semnalului 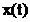 raportata la
fundamentala spectrului discret. Daca se tine cont ca
raportata la
fundamentala spectrului discret. Daca se tine cont ca 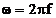 si
si 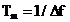 functia (2.37) se
pune sub forma:
functia (2.37) se
pune sub forma:
v
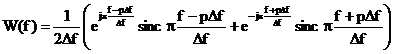 . (2.38)
. (2.38)
v
Calculele
implicate de aflarea amplitudinii functiei (2.38) 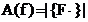 sunt mai complicate
in comparatie cu cele din (2.31) pentru ca amplitudinile celor doi
termeni se aduna vectorial, chiar daca spectrul de faza nu are
importanta.
sunt mai complicate
in comparatie cu cele din (2.31) pentru ca amplitudinile celor doi
termeni se aduna vectorial, chiar daca spectrul de faza nu are
importanta.
v 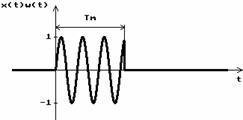
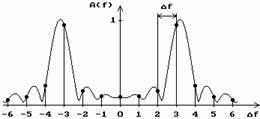
v Figura 2.7. Functiile 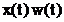 ,
, 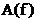 si
si 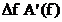 .
.
v
In
figura 2.7, in stanga, se prezinta semnalul continuu analizat 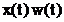 . In acest exemplu s‑au analizat
. In acest exemplu s‑au analizat 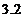 perioade ale
semnalului
perioade ale
semnalului 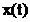 deci
deci 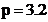 .
.
v
Tot
in figura 2.7, in dreapta, pe o axa continua a frecventei, prin
puncte se prezinta spectrul discret de amplitudine calculat cu formula
(2.20), (v. si (2.21), reprezentarea spectrului discret printr‑o distributie)
si spectrul continuu de amplitudine 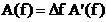 calculat analitic cu
formula (2.40).
calculat analitic cu
formula (2.40).
Erorile maxime de estimare a
amplitudinii unei linii spectrale
v
Semnalul
periodic 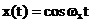 , daca este analizat cu seria Fourier conduce la un spectru
cu doua linii spectrale cu frecventele
, daca este analizat cu seria Fourier conduce la un spectru
cu doua linii spectrale cu frecventele 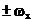 . In sectiunea precedenta, a fost trunchiat la
. In sectiunea precedenta, a fost trunchiat la 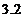 perioade si
analizat prin transformata Fourier discreta. S‑a obtinut
spectrul din figura 2.7 care are mai mult de doua linii spectrale, nici
una dintre ele nu are amplitudinea calculata prin seria Fourier.
perioade si
analizat prin transformata Fourier discreta. S‑a obtinut
spectrul din figura 2.7 care are mai mult de doua linii spectrale, nici
una dintre ele nu are amplitudinea calculata prin seria Fourier.
v
Pentru
ca in practica 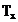 perioada semnalului
perioada semnalului 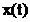 si
si 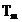 timpul de observare al
semnalului
timpul de observare al
semnalului 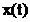 nu sunt corelate se
pune problema determinarii pe cale analitica a erorilor maxime de
evaluare a amplitudinii liniilor spectrale. Se disting doua cazuri:
nu sunt corelate se
pune problema determinarii pe cale analitica a erorilor maxime de
evaluare a amplitudinii liniilor spectrale. Se disting doua cazuri:
v
cazul
cel mai favorabil best
case): din semnal
sunt prelevate un numar intreg de perioade;
v
cazul
cel mai putin favorabil worst case):
cand din semnal sunt prelevate un numar intreg de perioade si
inca o semiperioada.
v
In
figurile 2.8 si 2.9 semnalul 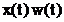 , coeficientii
, coeficientii 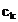 si spectrul
si spectrul 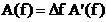 sunt prezentate la fel
ca in figura 2.8.
sunt prezentate la fel
ca in figura 2.8.
v 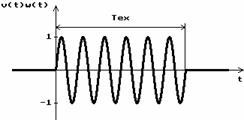
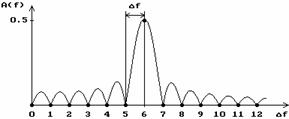
v Figura 2.8. Cazul cel mai favorabil, 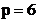 , adica
, adica 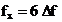
v
In
exemplul din figura 2.8 s‑au prelevat 6 perioade ale semnalului armonic 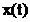 deci frecventa
fundamentala a semnalului
deci frecventa
fundamentala a semnalului 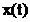 este
este 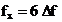 (v. notatiile
facute pentru formula (2.38) din sectiunea 2.3.2). In cazul cel mai
favorabil prin transformata Fourier discreta se obtine acelasi
rezultat ca si prin seria Fourier pentru ca
(v. notatiile
facute pentru formula (2.38) din sectiunea 2.3.2). In cazul cel mai
favorabil prin transformata Fourier discreta se obtine acelasi
rezultat ca si prin seria Fourier pentru ca 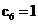 este echivalent cu
este echivalent cu 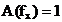 . In plus
. In plus 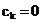 pentru
pentru 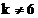 .
.
v 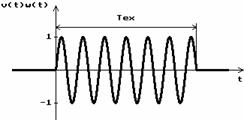
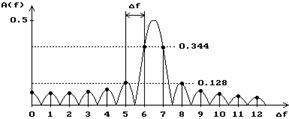
v Figura 2.9. Cazul cel mai putin
favorabil, 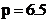 , adica
, adica 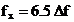
v
In
exemplul din figura 2.9 s‑au prelevat 6.5 perioade ale semnalului armonic
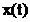 deci frecventa
fundamentala a semnalului
deci frecventa
fundamentala a semnalului 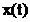 este
este 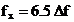 . In spectrul prezentat in figura din dreapta se
observa ca
. In spectrul prezentat in figura din dreapta se
observa ca 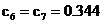 ceea ce inseamna
ca
ceea ce inseamna
ca 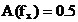 amplitudinea fundamentalei semnalului
amplitudinea fundamentalei semnalului 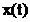 este estimata cu
o eroare de
este estimata cu
o eroare de
v
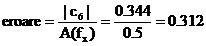 , (2.39)
, (2.39)
v
adica
31 %, iar coeficientii 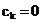 pentru
pentru 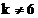 si
si 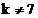 sunt estimati cu
o eroare maxima de 25.4 %.
sunt estimati cu
o eroare maxima de 25.4 %.
Concluzii
v
In ceea ce priveste
corelatia dintre proprietatile semnalului fizic  si
si 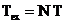 , timpul de observare a semnalului
, timpul de observare a semnalului  se disting patru cazuri:
se disting patru cazuri:
v
semnalul  este periodic si
este periodic si 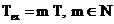 , adica timpul de masura este un multiplu al
perioadei semnalului
, adica timpul de masura este un multiplu al
perioadei semnalului 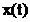 . Transformata Fourier discreta
devine un caz particular al seriei Fourier, in care coeficientii Fourier
se calculeaza dintr-un semnal esantionat;
. Transformata Fourier discreta
devine un caz particular al seriei Fourier, in care coeficientii Fourier
se calculeaza dintr-un semnal esantionat;
v
semnalul  este periodic, dar timpul de observare a
semnalului
este periodic, dar timpul de observare a
semnalului 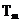 si perioada semnalului
si perioada semnalului 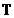 nu sunt corelate. In
aceasta situatie, semnalul
nu sunt corelate. In
aceasta situatie, semnalul  are un spectru de linii si transformata
Fourier discreta da rezultate foarte bune;
are un spectru de linii si transformata
Fourier discreta da rezultate foarte bune;
v
semnalul  , vizualizat cu un osciloscop, are
aspect periodic si este posibil sa fie generat de un proces fizic
periodic. Un astfel de semnal se numeste "quasiperiodic" pentru ca
asupra semnalului se poate formula doar o ipoteza de periodicitate.
Rezultatele date de transformata Fourier discreta sunt bune;
, vizualizat cu un osciloscop, are
aspect periodic si este posibil sa fie generat de un proces fizic
periodic. Un astfel de semnal se numeste "quasiperiodic" pentru ca
asupra semnalului se poate formula doar o ipoteza de periodicitate.
Rezultatele date de transformata Fourier discreta sunt bune;
v
semnalul  este aleator si in consecinta
nu este nici o corelatie intre timpul de observare a semnalului
este aleator si in consecinta
nu este nici o corelatie intre timpul de observare a semnalului 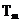 si continutul semnalului. In
aceasta situatie, transformata Fourier discreta este dificil
de aplicat nu se poate cunoaste modul in care trunchierea in timp
modifica forma spectrului. Exista totusi metoda medierii
spectrelor de putere, metoda care reduce aceasta influenta;
si continutul semnalului. In
aceasta situatie, transformata Fourier discreta este dificil
de aplicat nu se poate cunoaste modul in care trunchierea in timp
modifica forma spectrului. Exista totusi metoda medierii
spectrelor de putere, metoda care reduce aceasta influenta;
v
in subcapitolul 2.3 s‑a
studiat doar influenta ferestrei rectangulare asupra unui semnal armonic.
In capitolul 4 se vor studia si alte functii de ponderare care reduc
diferentele dintre cazul cel mai favorabil si cel mai putin
favorabil constatat in sectiunea 3.3.3 si erorile care apar prin
esantionarea unui spectru continuu cu de relatia (2.26) (v. figura
2.4 si comentariul din sectiunea 2.2.6).


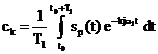
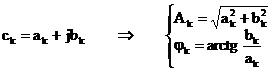
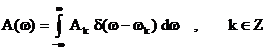
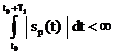
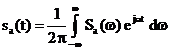
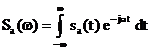

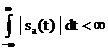

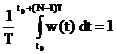 (2.14)
(2.14)