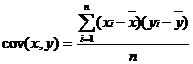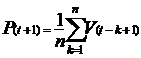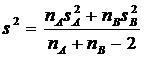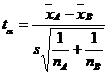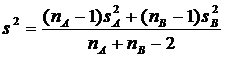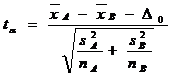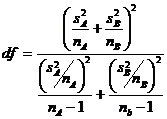ANALIZE STATISTICE, INGINERESTI SI FINANCIARE
In Excel aveti
doua metode principale cu ajutorul carora puteti face diferite
analize statistice, ingineresti, sau financiare:
Puteti sa
introduceti in foaia de calcul formulele statistice, ingineresti, sau
financiare pe care le doriti. In aceste formule puteti sa
folositi ca operanzi si anumite functii statistice,
ingineresti, sau financiare dintre cele pe care vi le ofera Excel,
daca aceste functii returneaza valori.
Puteti sa
folositi instrumentele din Analysis
ToolPak. Unui astfel de instrument trebuie sa‑i indicati
datele de intrare, pentru a va oferi analiza ceruta intr‑un
tabel de iesire, pe baza unor formule adecvate, prestabilite, pe care
dumneavoastra nici nu le vedeti. Unele instrumente de acest fel
genereaza si grafice.
Prima metoda cere un
efort mai mare din partea dumneavoastra, deoarece pe langa
pregatirea datelor de intrare, trebuie sa construiti formulele
care se aplica asupra acestor date. Folositi aceasta metoda
daca nu gasiti printre instrumentele din Analysis ToolPak nici
unul care sa va satisfaca. In formulele pe care le
construiti puteti folosi ca operanzi functii standard oferite de
Excel. Aceste functii sunt descrise in paragraful "Care sunt functiile
pe care vi le ofera Excel?".
A doua metoda este
mai simpla, deoarece Excel face aproape totul dupa ce i‑ati
pregatit datele de intrare. Trebuie doar sa stiti sa
apelati instrumentul potrivit din Analysis
ToolPak. Pentru a vizualiza lista instrumentelor de analiza pe care vi
le ofera Excel, apelati comanda Tools
| Data Analysis . . Daca
in meniul Tools nu apare
comanda Data Analysis . ,
probabil ca nu au fost instalate aceste instrumente, sau nu au fost
activate inca. Pentru a instala instrumentele de analiza, trebuie
sa relansati programul Setup
din kit-ul de instalare. Pentru a activa aceste instrumente, trebuie sa
urmati procedura de activare a facilitatilor extinse.
Aceasta procedura este descrisa in paragraful urmator.
Cum folositi anumite
facilitati extinse?
Pentru a activa
instrumentele de analiza din Analysis
ToolPak, procedati in felul urmator:
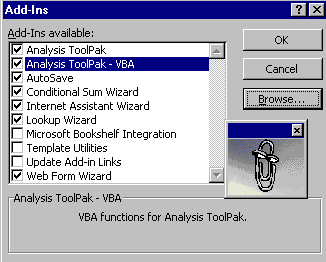
Apelati comanda Tools | Add‑Ins .
pentru a aparea dialogul Add‑Ins. In lista Add‑Ins
available apar toate facilitatile extinse ale programului Excel,
care au fost instalate si sunt disponibile. Facilitatile care
sunt active au un marcaj in partea stanga, iar cele care nu sunt active nu
au acest marcaj.
Cautati facilitatea Analysis ToolPak in
aceasta lista si activati comutatorul care ii corespunde in
partea stanga.
Incheiati dialogul cu OK.
Pentru
a folosi un instrument de analiza din pachetul Analysis ToolPak, procedati in felul urmator:
Selectati domeniul de date pe
care vreti sa‑l analizati.
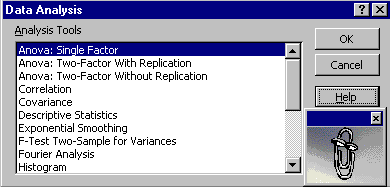
Apelati comanda Tools | Data Analysis . pentru a aparea fereastra de dialog Data Analysis.
Alegeti din lista Analysis Tools instrumentul de
analiza pe care il doriti.
Daca doriti ajutor, Office Assistant
va sta la dispozitie. Dupa ce ati ales din lista
instrumentul de analiza pe care il doriti, incheiati dialogul cu
OK.
Care sunt instrumentele
din pachetul Analysis ToolPak ?
In
continuare sunt enumerate instrumentele de analiza pe care vi le
ofera Excel in pachetul Analysis
ToolPak. La aceste instrumente aveti acces in fereastra de dialog Data Analysis, pe care o lansati
cu ajutorul comenzii Tools | Data Analysis . .
v
Testele
ANOVA (Analysis Of Variance) - Excel va ofera
urmatoarele trei teste statistice pentru analiza dispersiei
(variantei). Cu ajutorul acestor teste puteti verifica ipoteza nula ca mediile a
doua sau mai multor esantioane sunt egale (adica
esantioanele sunt extrase din populatii care au aceeasi medie
teoretica).
Anova:
Single Factor - Analiza simpla a dispersiei.
Anova:
Two-Factor With Replication - Analiza dispersiei, considerand
mai mult de un esantion pentru fiecare grup de date.
Anova:
Two-Factor Without Replication - Analiza dispersiei, considerand
un singur esantion pentru fiecare grup de date.
v
Covariance
(Covarianta) - Acest parametru statistic este o masura a
relatiei dintre doua serii de date de aceeasi dimensiune n. Daca notam cele doua
serii de date cu (xi)
si (yi), unde i ia valori de la 1 la n, formula dupa care se
calculeaza covarianta este urmatoarea:
unde
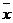 este media seriei (xi);
este media seriei (xi);
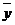 este media seriei (yi).
este media seriei (yi).
Dupa
cum reiese din formula de mai sus, covarianta este dependenta de
unitatea de masura in care sunt exprimate valorile celor doua
serii. Puteti folosi covarianta pentru a verifica daca datele
din cele doua serii variaza la fel. Daca valori mari dintr‑o
serie se asociaza cu valori mari din cealalta serie, covarianta
este pozitiva. Daca valori mari dintr‑o serie se asociaza
cu valori mici din cealalta serie, covarianta este negativa.
Daca valorile celor doua serii nu variaza la fel (nu exista
nici o relatie intre ele), covarianta este aproape de zero.
v
Correlation
(Corelatia, sau Coeficientul de corelatie) - Acest
parametru statistic este o masura a relatiei dintre doua
serii de date de aceeasi dimensiune n.
Daca notam cele doua serii de date cu (xi) si (yi),
unde i ia valori de la 1 la n, formula dupa care se
calculeaza covarianta este urmatoarea:
unde cov(x,
y) este covarianta celor
doua serii de date, iar S(x) si S(y) sunt abaterile
standard ale celor doua serii de date. Dupa cum se poate verifica in
formula de mai sus, coeficientul de corelatie r este o valoare
cuprinsa in intervalul [-1, 1]. De asemenea, valoarea coeficientului de
corelatie r nu depinde de
unitatea de masura in care sunt exprimate valorile celor doua
serii de date.
v
Descriptive
Statistics (Parametri statistici descriptivi) -
Aceasta optiune va genereaza un raport cu parametrii
statistici pentru un esantion de date corespunzator unei variabile
aleatoare. Acesti parametri statistici va ofera informatii
in legatura cu tendintele de centralitate (diferite medii),
precum si despre variabilitatea (dispersia, abaterea standard) datelor din
esantion.
v
Exponential
Smoothing (Estimare exponentiala) -
Folositi aceasta optiune pentru a obtine o prezicere (o
estimare) a unor valori pe baza valorilor din perioadele precedente. In
aceasta prezicere se acorda o pondere mai mare datelor mai recente.
v
F-Test
Two-Sample for Variances - Cu ajutorul acestei optiuni
puteti efectua testul F pentru
compararea dispersiilor a doua esantioane care provin din doua
populatii. De exemplu, puteti folosi testul F pentru a determina
daca intr‑un concurs de atletism pe echipe, exista o deosebire
semnificativa intre dispersiile timpilor obtinuti in cadrul a
doua echipe.
v
Fourier
Analysis - Cu ajutorul acestei optiuni puteti rezolva
probleme care includ sisteme liniare si analiza datelor periodice,
folosind metoda transformatei Fourier
rapide (FFT - Fast Fourier Transform) pentru a transforma datele. De
asemenea, acest instrument permite si transformari inverse, in care
prin inversarea datelor transformate se ajunge la datele initiale.
v
Histogram -
Aceasta optiune va permite sa calculati
frecventele de aparitie ale unor valori intr‑un domeniu de
celule. Puteti calcula frecvente individuale, sau frecvente
cumulate, pe grupe de valori.
v
Moving
Average - Folosind aceasta optiune puteti prevedea
anumite valori ale unei variabile aleatoare pentru o perioada viitoare, pe
baza valorilor medii ale variabilei respective, calculate pentru un numar
dat de perioade precedente. Fiecare valoare prezisa pentru viitor se
calculeaza cu ajutorul formulei:
unde
n -
este numarul de perioade precedente pe baza carora se calculeaza
valoarea prezisa pentru viitor;
Vj -
este valoarea variabilei aleatoare in momentul j.
Pj -
este valoarea variabilei aleatoare prezisa pentru momentul j.
In
felul acesta, pe baza unor simple medii efectuate asupra unor date de
arhiva, puteti obtine prognoze pentru vanzari, inventar,
profit, etc. Analizand tendintele acestor variabile aleatoare, puteti
initia anumite proiecte pentru viitor.
v
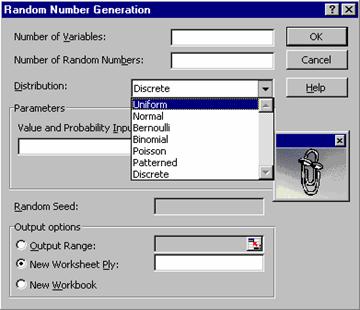
Random
Number Generation - Aceasta optiune va permite sa
umpleti un domeniu de celule cu numere aleatoare independente, generate pe
baza unei repartitii (distributii) specificate. Daca
apelati aceasta facilitate, apare o fereastra de dialog in care
trebuie sa precizati anumiti parametri. Din lista ascunsa Distribution, puteti alege repartitia
care sa stea la baza generarii numerelor aleatoare. In functie
de repartitia pe care o alegeti in fereastra de dialog, apar
anumiti parametri care determina repartitia respectiva.
Puteti alege una din urmatoarele repartitii:
Uniform
- Repartitia uniforma este caracterizata prin
o valoare inferioara si o valoare superioara. Numerele aleatoare
sunt generate in mod uniform intre cele doua limite, cu
probabilitati egale. O repartitie uniforma
standardizata genereaza valori intre limitele 0 si 1.
Normal
- Repartitia normala este caracterizata de o medie si o abatere standard. O repartitie normala standardizata
are media egala cu 0 si abaterea standard egala cu 1.
Bernoulli
- Repartitia Bernoulli este caracterizata de un
parametru p, care reprezinta
probabilitatea de a avea succes intr‑o proba. O variabila
aleatoare de tip Bernoulli poate lua valoarea 1 (succes), sau 0 (insucces).
Pentru a genera o variabila de tip Bernoulli, se poate folosi o
variabila aleatoare uniforma in intervalul [0, 1]. Daca
variabila aleatoare uniforma are o valoare mai mare decat p, variabila aleatoare de tip Bernoulli
ia valoarea 1, in caz contrar ia valoarea 0.
Binomial - Repartitia binomiala este
caracterizata de doi parametri. Primul parametru este probabilitatea p de a avea succes intr‑o
proba, iar al doilea este numarul de probe n.
Poisson - Repartitia Poisson este caracterizata
de un singur parametru, care este egal cu media variabilei aleatoare (dispersia
acestei repartitii este egala
cu media) si care se numeste Lambda.
Aceasta repartitie se
foloseste pentru a caracteriza numarul de evenimente care au loc intr‑o
unitate de timp.
Patterned - Aceasta repartitie este caracterizata de o
limita inferioara, o limita superioara si un pas.
Valorile sunt generate intre cele doua limite, la distante egale cu
pasul (al treilea parametru). Prin urmare, valorile acestei repartitii alcatuiesc o serie (o
progresie aritmetica).
Discrete - In aceasta repartitie fiecarei valori i se
asociaza o probabilitate de aparitie. Suma tuturor
probabilitatilor trebuie sa fie egala cu 1.
Random Seed - Introduceti
o valoare optionala, pornind de la care vor fi generate numerele
aleatoare. Daca ulterior reutilizati aceeasi valoare, vor fi
generate aceleasi numere aleatoare.
v
Rank
and Percentile - Acest instrument creaza un raport care
contine numarul de ordine si repartitia procentuala pentru
fiecare valoare din setul de date. Puteti folosi aceasta facilitate
pentru a analiza pozitia relativa a valorilor in setul de date.
v
Regression -
Acest instrument efectueaza o analiza de regresie liniara folosind metoda celor mai mici patrate
pentru a genera o dreapta care se apropie cel mai mult de un set de
valori. Puteti folosi aceasta facilitate pentru a vedea cum este
afectata o variabila dependenta de valorile uneia sau mai multor
variabile independente. De exemplu, puteti determina cum sunt afectate vanzarile
unei societati comerciale de cheltuielile facute pentru
marketing. De asemenea, puteti vedea cum sunt afectate performantele
unui atlet de anumiti factori, cum sunt varsta, greutatea si
inaltimea. Pentru aceasta, completati in foaia de calcul
valorile celor trei parametri in cazul unei performante cunoscute, apoi
folositi regresia pentru a prezice performantele unor atleti
noi, necunoscuti.
v
Sampling -
Acest instrument creaza un esantion, considerand ca domeniul
selectat de celule este o populatie. Daca populatia este prea
mare pentru a se face o analiza sau un grafic, puteti folosi un
esantion reprezentativ. De asemenea, puteti crea un esantion
care contine numai valori dintr‑o anumita parte a unui ciclu,
daca credeti ca datele de intrare sunt periodice. De exemplu,
daca datele de intrare reprezinta vanzari trimestriale,
puteti face esantionarea pentru acelasi trimestru folosind o
rata periodica egala cu patru.
v
t-Test:
Paired Two Sample For Means - Cu ajutorul acestei optiuni
puteti efectua testul t (numit
si testul Student) pentru
doua esantioane perechi, pentru a determina daca mediile celor
doua esantioane difera semnificativ. Aceasta forma a
testului t nu presupune ca dispersiile celor doua populatii sunt
egale. Puteti folosi acest test cand exista o imperechere
naturala a observatiilor din cele doua esantioane, cum ar
fi testarea unui esantion pentru un grup de doua ori - inainte
si dupa un experiment. De exemplu, folositi acest test cand
comparati anumite analize medicale pentru un pacient, inainte si
dupa un tratament.
Printre
alte rezultate pe care vi le ofera acest test este si o dispersie globala (pooled variance), pentru intreaga
populatie, pe baza urmatoarei
formule:
Cu ajutorul acestei dispersii globale se calculeaza parametrul
statistic t pe baza
urmatoarei formule:
Numarul
de grade de libertate in cazul acestui test este egal cu numarul de probe
din cadrul unui esantion minus unu. Esantioanele fiind perechi,
numarul de probe din cele doua esantioane sunt egale (n = nA = nB), iar
numarul de grade de libertate este df
= n-1.
v
t-Test:
Two-Sample Assuming Equal Variances - Cu ajutorul acestei
optiuni puteti efectua o alta varianta a testului t (Student) pentru doua esantioane. Aceasta forma
a testului t presupune ca
dispersiile celor doua seturi de date sunt egale (se mai numeste testul t homoscedastic). Puteti
folosi acest test pentru a determina daca mediile celor doua
esantioane sunt egale. Dispersia globala in acest caz se
calculeaza astfel:
Parametrul
statistic t se
calculeaza pe baza aceleiasi formule ca in cazul de mai sus.
Numarul de grade de libertate in cazul acestui test este dat de formula df = nA+nB-2.
v
t-Test:
Two-Sample Assuming Unequal Variances - Cu
ajutorul acestei optiuni puteti efectua o alta varianta a testului t (Student) pentru doua esantioane. Aceasta forma
a testului t presupune ca
dispersiile celor doua domenii de valori nu sunt egale (se mai
numeste testul t heteroscedastic).
Puteti folosi acest test pentru a determina daca mediile celor
doua esantioane sunt egale. Folositi aceasta varianta
cand grupurile de date care se studiaza sunt distincte.
Parametrul
statistic t se calculeaza pe baza urmatoarei formule:
Pentru a aproxima numarul gradelor de libertate se foloseste
formula:
Intrucat
valoarea rezultata din aceasta formula nu este un numar
intreg, se foloseste cel mai apropiat intreg pentru a gasi
numarul de grade de libertate.
v
z-Test:
Two-Sample For Means - Cu ajutorul acestei optiuni
puteti efectua testul z pentru
doua esantioane cu dispersii cunoscute. Folositi acest test
pentru a determina ipotezele in legatura cu diferentele dintre
mediile a doua populatii.
3. Testul t pentru doua esantioane perechi
Testul t (Student) pentru esantioane perechi il puteti
folosi cand vreti sa comparati rezultatele a doua
experimente, sau efectele a doua tratamente. De exemplu, sunt
situatii in care vreti sa comparati un tratament nou cu
unul traditional, sau un experiment nou cu unul standard. In aceste
situatii trebuie sa creati doua esantioane perechi.
Aveti doua posibilitati de a crea aceste esantioane
perechi:
Puteti folosi acelasi esantion a doua
oara, ulterior, in alte conditii;
Puteti alege doua esantioane
diferite, pe care apoi le imperecheati.
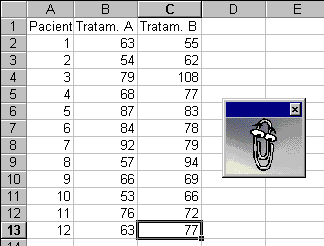
In acest exemplu
veti compara efectele pe care le au doua tipuri de tratamente cu
tarate petru tratarea diverticulozei. Studiul se face cu un
esantion de 12 pacienti de varsta intre 20 si 44 de ani,
pentru care gravitatea bolii este cam aceeasi. Pentru a crea doua
esantioane perechi de date, tuturor pacientilor li se
administreaza cele doua tratamente succesiv, in doua momente
diferite. Ordinea celor doua tratamente pentru fiecare pacient se
stabileste cu ajutorul unui tabel de numere aleatoare. Cele doua
tratamente care se compara sunt urmatoarele:
Tratamentul A - Administrarea unei
doze de tarate la o masa pe zi;
Tratamentul B - Administrarea aceleiasi doze de
tarate la trei mese pe zi.
Pentru a compara cele doua tratamente,
se socoteste dupa fiecare tratament timpul necesar pentru tranzitul
intestinal, in ore. Construiti o foaie de calcul, in care
inregistrati numarul de ore necesare pentru tranzitul intestinal,
pentru fiecare pacient si pentru fiecare tratament, ca in figura de mai sus.
Cele doua serii de numere pe care le inregistrati in coloanele
"Tratam. A" si "Tratam. B" se vor compara pentru a stabili daca
rezultatele obtinute in urma celor doua tratamente difera
semnificativ sau nu.
Pentru a obtine parametrii statistici cu
ajutorul testului t pentru
esantioane perechi, procedati in felul urmator:
Activati foaia de calcul care contine
datele pe care vreti sa le comparati.
Apelati comanda Tools | Data
Analysis . pentru a aparea fereastra de dialog Data Analysis.
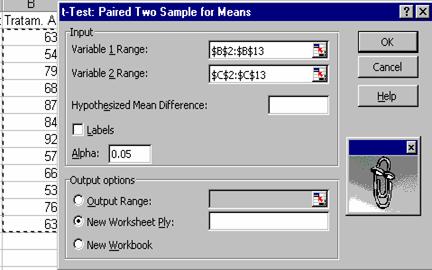
In fereastra de dialog Data Analysis parcurgeti lista Analysis Tools si alegeti optiunea. t-Test: Paired Two Sample For Means,
apoi incheiati aceasta fereastra de dialog cu OK.
Pe ecran apare imediat fereastra de dialog t-Test: Paired Two Sample For Means, in
care trebuie sa precizati anumiti parametri. In campul Variable 1 Range introduceti
domeniul de celule $B$2:$B$13 unde se afla prima serie (datele din coloana
"Tratam. A"), iar in campul Variable 2
Range introduceti domeniul de celule $C$2:$C$13 unde se afla a
doua serie (datele din coloana "Tratam. A").
In afara de
cele doua serii de date pe care trebuie sa le precizati in
campurile Variable 1 Range
si Variable 2 Range, mai
exista parametrul Alpha
pe care orice statistician il stie, el reprezentand nivelul
semnificatiei cu care vreti sa lucrati (semnificatia ipotezei nule, sau
riscul de a respinge ipoteza nula cand ea este adevarata). In
mod implicit acest parametru este egal cu 0.05,
ceea ce inseamna ca lucrati cu o probabilitate de 95%. In
chenarul Output options puteti
preciza anumite optiuni in legatura locul unde va fi generat
raportul care contine rezultatul compararii. In acest chenar sunt
prezente urmatoarele butoane radio, din care alegeti unul:
Output Range - Daca
actionati acest buton radio, se activeaza campul din dreapta in
care trebuie sa introduceti adresa domeniului de celule (din foaia de
calcul curenta) in care va fi generat raportul.
New Worksheet Ply
-
Daca actionati acest buton radio, se activeaza campul din
dreapta in care trebuie sa introduceti un nume pentru o foaie de
calcul noua, care va fi generata in registrul de lucru curent, pentru
a putea fi creat raportul. Numele foii de calcul trebuie sa nu
coincida cu numele altei foi de calcul din registrul curent.
New Workbook - Daca
actionati acest buton radio, se genereaza automat un nou
registru de lucru cu un nume standard, raportul fiind generat intr‑o
foaie de calcul a acestui registru. Cand veti salva acest registru de
lucru, puteti sa‑i dati un nume semnificativ.
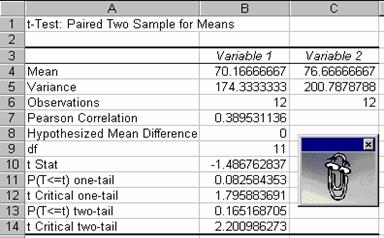
Dupa ce ati precizat toti parametrii,
actionati butonul OK. Pe
ecran va aparea imediat un raport care contine un tabel cu mai
multi parametri statistici intr‑un format standard prestabilit. Un
statistician poate sa interpreteze cu usurinta acesti
parametri. In primele trei linii se afla mediile, dispersiile si
numarul de observatii pentru cele doua esantioane.
Numarul de grade de libertate df
este egal cu 11 (numarul de probe minus 1). Parametrul t Stat defineste valoarea lui t care ne ajuta sa stabilim
daca exista sau nu diferente semnificative intre rezultatele
celor doua tratamente (parametrul t din formula
prezentata in paragraful anterior).
Pentru 11 grade de libertate, valoarea
teoretica a parametrului t este
data de parametrul t Critical two‑tail
si este aproximativ egala cu 2.201 (daca se face calculul
manual, aceeasi valoare se scoate din tabelul repartitiei t). Valoarea
calculata a parametrului t este de aproximativ 1.487 (se ia valoarea
absoluta din rubrica t Stat).
Intrucat valoarea calculata a parametrului t este mai mica decat valoarea
teoretica, este adevarata ipoteza
nula ca nu exista o diferenta semnificativa
intre mediile celor doua serii de date. Cu alte cuvinte, nu
exista diferente semnificative
intre timpii medii necesari pentru tranzitul intestinal, in urma celor
doua tratamente.
Daca aveti un tabel cu repartitia
t, observati ca valoarea calculata t =1.487 este cuprinsa
intre valorile 1.363 si 1.796, ceea ce inseamna ca
probabilitatea p (semnificatia
ipotezei nule) este cuprinsa intre 0.2 si 0,1 (0.2 > p > 0.1).
4. Testul t presupunand dispersiile egale
Pentru
a determina pH‑ul unei solutii, se fac doua serii de
masuratori repetate, cu doua aparate diferite. Bineinteles
ca se obtin valori diferite, oricat de bine ar fi reglate cele
doua aparate. Intrebarea pe care ne‑o punem este daca
exista diferente semnificative intre mediile masuratorilor
facute cu cele doua aparate. Daca diferentele sunt
semnificative, ar putea insemna ca unul din aparate este defect. Aceasta
metoda se poate folosi pentru verificarea unui aparat prin compararea cu
un alt aparat standard.
Pentru a raspunde la aceasta
intrebare, procedati in felul urmator:
Introduceti intr‑o foaie de calcul cele
doua serii de masuratori, facute cu cele doua aparate
A si B.
Apelati comanda Tools | Data Analysis . pentru a aparea fereastra
de dialog Data Analysis.
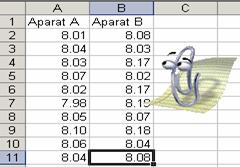
In fereastra de dialog Data Analysis parcurgeti lista Analysis Tools si alegeti optiunea. t-Test: Two-Sample Assuming Equal
Variances, apoi incheiati aceasta fereastra de dialog cu OK.
Pe ecran apare imediat fereastra de dialog t-Test: Two-Sample Assuming Equal Variances,
in care trebuie sa precizati anumiti parametri. Aceasta
fereastra de dialog este asemanatoare cu cea din paragraful
precedent, dar bineinteles ca are un titlu corespunzator.
Verificati valorile parametrilor si modificati‑le pe cele
care trebuie.
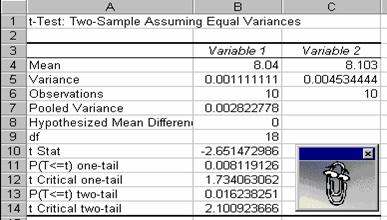
Dupa ce ati precizat toti parametrii,
actionati butonul OK. Pe
ecran va aparea imediat un raport care contine un tabel cu mai
multi parametri statistici intr‑un format standard prestabilit. Un
statistician poate sa interpreteze cu usurinta acesti
parametri. In primele trei linii se afla mediile, dispersiile si
numarul de observatii pentru cele doua esantioane. Numarul
de grade de libertate df este egal
cu 18. Acest numar se obtine din formula prezentata in
paragraful 2, considerandu‑se un esantion global prin combinarea
celor doua esantioane. Conform formulei, df = (10-1) + (10-1).
Parametrul t Stat defineste
valoarea lui t care ne ajuta sa
stabilim daca exista sau nu diferente semnificative intre cele
doua serii de masuratori (parametrul t din formula prezentata
in paragraful 2).
Pentru 18 grade de libertate, valoarea
teoretica a parametrului t este
data in rubrica t Critical two‑tail
si este aproximativ egala cu 2.101 (daca se face calculul
manual, aceeasi valoare se scoate din tabelul repartitiei t). Valoarea
calculata a parametrului t este de aproximativ 2.65 (se ia valoarea
absoluta din rubrica t Stat).
Intrucat valoarea calculata a parametrului t este mai mare decat valoarea teoretica,
diferenta dintre mediile celor doua serii de date este
semnificativa. Cu alte cuvinte, exista o diferenta
semnificativa intre valorile medii ale masuratorilor efectuate
cu cele doua aparate. Valoarea probabilitatii p (semnificatia ipotezei nule) este
cuprinsa intre 0.02 si 0,01 (0.02 > p > 0.01).
5. Coeficientul de corelatie
Pentru a studia
corelatia care exista intre cheltuielile pentru marketing si
vanzarile efectuate pe parcursul unui an, alcatuiti un tabel cu
trei coloane in care introduceti in prima coloana lunile anului, in a
doua coloana cheltuielile pentru marketing, iar in a treia coloana
vanzarile efectuate in fiecare luna (pentru a nu introduce numere prea
mari, le puteti trunchia la milioane, sau miliarde), ca in figura de mai
jos.
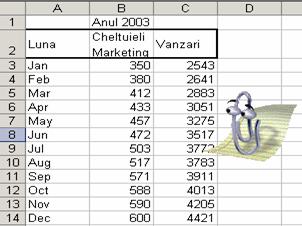
Dupa ce ati introdus cele doua
serii de date, procedati in felul urmator:
Daca foaia de calcul in care sunt prezente cele
doua serii de date este activa, apelati comanda Tools | Data Analysis .
pentru a aparea fereastra de dialog Data
Analysis.
In fereastra de dialog Data Analysis parcurgeti lista Analysis Tools si alegeti optiunea Correlation, apoi incheiati
aceasta fereastra de dialog cu OK.
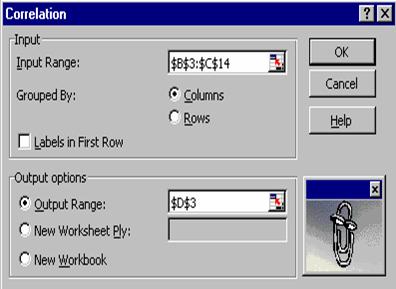
Pe ecran apare imediat fereastra de dialog Correlation, in care trebuie sa
precizati anumiti parametri.
In campul Input
Range introduceti domeniul de celule care contine cele doua
serii de date.
Datele fiind introduse pe coloane, activati
butonul radio Columns,
daca nu este activ deja.
Intrucat raportul de iesire contine
putine date, puteti sa le scoateti pe aceeasi foaie de
calcul alaturi de tabel. Activati butonul radio Output Range, iar in campul din partea dreapta
introduceti adresa celulei D3, care va fi adresa de inceput a domeniului
unde va fi scos raportul de iesire.
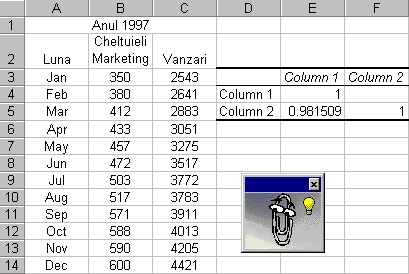
Incheiati dialogul cu OK. Pe ecran va aparea un raport care contine
coeficientul de corelatie intre cele doua serii de date. Raportul are
forma unui tabel cu doua linii si doua coloane, deoarece se
returneaza cate un coeficient de corelatie pentru fiecare
combinatie de coloane din domeniul de intrare. Cand se compara o
coloana cu ea insasi, coeficientul de corelatie este egal
cu 1, deoarece datele coincid. Coeficientul de corelatie rezultat din
compararea coloanei 1 cu coloana 2 este egal aproximativ cu 0.98. Acest coeficient de
corelatie fiind aproape de 1, rezulta ca intre datele din cele
doua coloane exista o corelatie semnificativa.
Pentru un anumit nivel de probabilitate
si un anumit numar de grade de libertate (numarul de grade de
libertate df este egal cu n-2, unde n este dimensiunea seriilor care se compara), se poate calcula
valoarea teoretica a coeficientului de corelatie r. De exemplu, pentru probabilitatea de 95% (p=0.05), in tabelul de
mai jos sunt date valorile teoretice ale coeficientului de corelatie r, in functie de numarul de
grade de libertate:
Daca valoarea r obtinuta
pentru un anumit grad de libertate este mai mare decat valoarea
corespunzatoare din tabel, exista o corelatie semnificativa
intre cele doua serii de date. In caz contrar, este improbabil sa
existe o corelatie semnificativa intre cele doua serii de date.
6. Care sunt functiile pe care vi le ofera Excel?
Functiile
pe care vi le ofera Excel sunt grupate in urmatoarele categorii:
v
Functii pentru baze de date si liste;
v
Functii pentru date calendaristice si ore;
v
Functii financiare;
v
Functii matematice;
v
Functii trigonometrice;
v
Functii statistice;
v
Functii pentru texte;
v
Functii pentru informare;
v
Functii pentru cautare si adresare;
v
Functii logice;
v
Functii ingineresti.
6.1. Functii pentru baze de date si liste
Excel va ofera o multime
de functii pentru prelucrarea bazelor de date si a listelor. Toate
aceste functii folosesc aceiasi parametri, care au urmatoarele
semnificatii:
baza de date - Acest parametru
precizeaza baza de date care face obiectul acestei functii. Ca
valoare pentru acest parametru puteti folosi un domeniu, sau numele unui
domeniu de celule. Pentru a defini numele unui domeniu de celule, folositi
comanda Insert | Name | Define . .
camp - Acest parametru
precizeaza campul (sau coloana) care contine datele asupra
carora opereaza functia. Puteti folosi numele unui camp
inclus intre ghilimele (de exemplu "Vanzari"), sau numarul coloanei
(se considera numerotarea coloanelor de la stanga la dreapta: 1, 2, 3,
etc.).
criteriu - Acest parametru
reprezinta criteriul pentru selectarea datelor din baza de date, asupra
carora va opera functia. Ca valoare a acestui parametru puteti
folosi o referinta, sau un nume.
Functiile pentru prelucrarea bazelor de
date si a listelor sunt urmatoarele:
DAVERAGE(baza
de date, camp, criteriu) - Aceasta functie calculeaza media
numerelor din campul indicat al bazei de date, pentru inregistrarile care
satisfac criteriul specificat.
DCOUNT(baza de
date, camp, criteriu) - Aceasta functie numara
inregistrarile numerice din campul indicat al bazei de date, care satisfac
criteriul specificat.
DCOUNTA(baza de
date, camp, criteriu) - Aceasta functie numara celulele
cu continut nenul din campul indicat al bazei de date, care satisfac
criteriul specificat.
DGET(baza de
date, camp, criteriu) - Aceasta functie extrage din baza de date
o singura inregistrare, dintre inregistrarile care satisfac criteriul
specificat. Daca nici una din inregistrarile bazei de date nu
satisface criteriul specificat, se returneaza valoarea de eroare #VALUE!.
Daca exista mai multe inregistrari care satisfac criteriul
specificat, se returneaza valoarea de eroare #NUM!.
DMAX(baza de
date, camp, criteriu) - Aceasta functie gaseste
numarul maxim pentru campul indicat al bazei de date, considerand
inregistrarile care satisfac criteriul specificat.
DMIN(baza de
date, camp, criteriu) - Aceasta functie gaseste
numarul minim pentru campul indicat al bazei de date, considerand
inregistrarile care satisfac criteriul specificat.
DPRODUCT(baza
de date, camp, criteriu) - Aceasta functie inmulteste
valorile pentru campul indicat al bazei de date, considerand
inregistrarile care satisfac criteriul specificat.
DSTDEV(baza de
date, camp, criteriu) - Aceasta functie calculeaza abaterea
standard pentru un esantion de date, pe baza numerelor din campul indicat al bazei de
date, considerand inregistrarile care satisfac criteriul specificat.
DSTDEVP(baza de
date, camp, criteriu) - Aceasta functie calculeaza abaterea
standard pentru intreaga populatie, pe baza numerelor din campul indicat
al bazei de date, considerand inregistrarile care satisfac criteriul
specificat.
DSUM(baza de
date, camp, criteriu) - Aceasta functie insumeaza valorile
din campul indicat al bazei de date, considerand inregistrarile care
satisfac criteriul specificat.
DVAR(baza de
date, camp, criteriu) - Aceasta functie calculeaza
dispersia (varianta) pentru un esantion de date, pe baza numerelor din campul indicat al bazei de
date, considerand inregistrarile care satisfac criteriul specificat.
DVARP(baza de
date, camp, criteriu) - Aceasta functie calculeaza
dispersia (varianta) pentru intreaga populatie, pe baza numerelor din campul indicat al bazei de
date, considerand inregistrarile care satisfac criteriul specificat.
SUBTOTAL(numar
functie, baza de date) - Aceasta functie creaza valoarea
unei functii de subtotal (identificata de primul parametru), pentru
elementele unei baze de date. Numerele de functii pe care le puteti
folosi in SUBTOTAL, precum si semnificatiile lor, sunt date in
tabelul urmator:
|
Numar functie
|
Functie
|
Semnificatie
|
|
AVERAGE
|
Media
|
|
COUNT
|
Numarul valorilor numerice
|
|
COUNTA
|
Numarul valorilor de orice tip
|
|
MAX
|
Elementul maxim
|
|
MIN
|
Elementul minim
|
|
PRODUCT
|
Produsul
|
|
STDEV
|
Abaterea standard pentru esantion
|
|
STDEVP
|
Abaterea standard pentru populatie
|
|
SUM
|
Suma
|
|
VAR
|
Dispersia pentru esantion
|
|
VARP
|
Dispersia pentru populatie
|
6.2. Functii pentru date calendaristice si ore
Cu toate ca
aveti posibilitatea de a introduce datele calendaristice si orele in
formate diferite, Microsoft Excel inregistreaza toate datele sub
forma unor siruri de numere (sau
numere seriale) si toate orele
sub forma unor fractii zecimale, pastrand si formatul pe care l‑ati
ales. In acest fel, Excel poate sa compare intre ele date
calendaristice sau ore introduse in formate diferite. In mod implicit,
Microsoft Excel pentru Windows foloseste calendarul incepand cu anul 1900
(la fel ca Lotus 1-2-3), iar Microsoft Excel pentru Macintosh foloseste
calendarul incepand cu anul 1904. Fractiile zecimale cuprinse intre 0.0
si 0.999 reprezinta orele unei zile incepand cu 00:00:00
(ore:minute:secunde), sau 12:00 AM (miezul noptii), pana la 23:59:59,
sau 11:59:59 PM. De exemplu, valoarea 0.25 reprezinta ora 6:00 AM (6/24,
sau 1/4 dintr‑o zi), iar valoarea 0.75 reprezinta ora 18:00 AM
(18/24, sau 3/4 dintr‑o zi). In Excel pentru Windows, valoarea 37980.5
reprezinta data de 25‑Dec-2003 ora 12:00 PM (amiaza). Partea
intreaga a numarului (de la stanga marcii zecimale)
reprezinta data calendaristica, iar partea fractionara (de
la dreapta marcii zecimale) reprezinta ora din ziua respectiva.
Orice data calendaristica poate fi exprimata intr‑un
format extern pentru a fi inteleasa mai bine de utilizatori si
intr‑un format intern, sub forma de numar serial, pentru a
putea opera mai bine cu ea. De exemplu, sa consideram data de
2 decembrie 2003 ora 17:30, care poate fi exprimata intr‑un
format european unitar in felul urmator: 02-12-2003 17:30. Aceeasi data poate fi exprimata in
format general, sub forma numarului
serial 37957.72917.
Functiile
pentru date calendaristice si ore pe care vi le ofera Excel sunt
urmatoarele:
v
DATE(an, luna,
zi) -
Aceasta functie returneaza numarul serial pentru data
specificata prin cei trei parametri. De exemplu, DATE(2003, 12, 24)
returneaza numarul serial 37979, sau data respectiva in formatul
ales.
v
DATEVALUE(data_text)
-
Aceasta functie efectueaza conversia unei date reprezentate sub
forma de text, in numar serial. Parametrul data_text este o data calendaristica in format
extern, care poate fi exprimata in orice format predefinit acceptat de
Excel. Parametrul poate fi o constanta de tip text, sau poate fi luat
dintr‑o celula. De exemplu, apelul functiei DATEVALUE("25-Dec-2003")
returneaza numarul serial 37980, sau data respectiva in formatul
ales.
v
DAY(data_calendaristica)
-
Aceasta functie converteste o data calendaristica
exprimata in format extern, sau sub forma de numar serial, in
numarul zilei din luna, in
intervalul dintre 1 si 31. De exemplu, functia DAY(37980)
returneaza valoarea 25, iar functia DAY("25-Dec-2003")
returneaza tot valoarea 25.
v
DAY360(data‑inceput,
data‑sfarsit [, metoda]) - Aceasta functie
afisaza numarul de zile scurs intre data‑inceput si data‑sfarsit, considerand anul de 360 de zile.
Parametrul optional metoda
are valoarea 1 pentru America si 2 pentru Europa (modifica valoarea
cand data‑inceput este
ziua de 30 sau 31 a lunii).
v
EDATE(data‑inceput,
luni)
- Aceasta functie afisaza numarul serial al datei
situate la un numar de luni
fata de data-inceput.
Aceasta functie este utila pentru calcule de imprumuturi. De
exemplu, apelul functiei EDATE("24-Dec-2003", 12) va returna numarul
serial 38345, iar daca se alege un format adecvat de data, valoarea
returnata este 24‑Dec‑2004.
v
EOMONTH(data‑inceput,
luni)
- Aceasta functie returneaza numarul serial al ultimei zile
a lunii din data care se afla la un numar de luni fata de data-inceput.
De exemplu, functia EOMONTH("24-Dec-2003", 12) va returna numarul
serial 38352, iar daca se alege un format adecvat de data, valoarea
returnata este 31‑Dec‑2004.
v
HOUR(data_calendaristica) - Aceasta
functie returneaza un numar intre 0 si 23 care
reprezinta ora din data
calendaristica transmisa ca parametru. De exemplu, functia
HOUR("24-Dec-2003 17:30") va returna valoarea 17 care reprezinta ora din
aceasta data, iar functia HOUR(379772917) va returna tot
valoarea 17.
v
MINUTE(data_calendaristica) - Aceasta
functie returneaza un numar intre 0 si 59 care
reprezinta numarul de minute
din data calendaristica transmisa ca parametru. De exemplu,
functia MINUTE("24-Dec-2003 17:30") va returna valoarea 30 care
reprezinta numarul de minute din aceasta data, iar
functia MINUTE(379772917) va returna tot valoarea 30.
v
MONTH(data_calendaristica) - Aceasta
functie returneaza un numar intre 0 si 12 care
reprezinta numarul lunii
din data calendaristica transmisa ca parametru. De exemplu,
functia MONTH("24-Dec-2003 17:30") va returna valoarea 12 care
reprezinta numarul lunii din aceasta data. Daca ora
este mai mare decat 24, Excel trece la ziua urmatoare cand face conversia
pentru a returna rezultatul. De exemplu, functia MONTH("31-Dec-2003
24:30:30") va returna valoarea 1, deoarece data de mai sus reprezinta de fapt
1 ianuarie 2004.
v
NETWORKDAYS(data_inceput,
data_sfarsit, vacanta) - Aceasta functie
returneaza numarul de zile lucratoare cuprinse intre data_inceput si data_sfarsit. Din intervalul
respectiv sunt excluse zilele de sbmbata si duminica,
precum si zilele de vacanta, sau concediu. De exemplu,
functia NETWORKDAYS("17-Nov-2003", "21-Dec-2003") va returna valoarea 25,
iar functia NETWORKDAYS("17-Nov-2003", "21-Dec-2003", "2-Dec-2003") va
returna valoarea 24.
v
NOW() - Aceasta
functie returneaza data calendaristica si ora, oferite de
ceasul intern al calculatorului. Excel actualizeaza data si ora
la fiecare activare si recalculare a foii de calcul. De exemplu, in data
de 23 septembrie 2003 ora 10 si 17 minute, aceasta functie
returneaza data si ora "9-23-2003 10:17" in format american, sau in
alt format ales. Daca se schimba formatul in unul general, valoarea
returnata este numarul serial 37887.42847.
v
SECOND(data_calendaristica) - Aceasta
functie returneaza un numar intre 0 si 59 care
reprezinta numarul de secunde
din data calendaristica transmisa ca parametru. De exemplu,
functia SECOND('23-sep-2003 10:17:37') va returna valoarea 37
care reprezinta numarul de secunde din aceasta data
calendaristica, iar functia SECOND(37887.428900463) va returna tot
valoarea 37.
v
TIME(ora,
minut, secunda) - Aceasta functie returneaza
numarul serial pentru valorile transmise prin cei trei parametri,
reprezentand ora, minutul si secunda. De exemplu, TIME(17, 30, 17)
returneaza numarul serial 0.729363426.
v
TIMEVALUE(timp_text)
-
Aceasta functie converteste o valoare de tip ora exprimata sub forma
de text, intr‑un numar serial. Parametrul timp_text este o data de tip ora in unul din formatele
externe acceptate de Excel. Parametrul poate fi o constanta de tip text,
sau poate fi luat dintr‑o celula. De exemplu, functia
TIMEVALUE("17:30:17") returneaza numarul serial 0.729363426,
functia TIMEVALUE("12.00 PM") returneaza numarul serial 0.5, iar
functia TIMEVALUE("12.00 AM") returneaza 0.
v
TODAY() - Aceasta
functie returneaza data calendaristica oferita de ceasul
intern al calculatorului. Functia TODAY() este asemanatoare cu
NOW(), dar spre deosebire de aceasta din urma, nu returneaza partea
fractionara corespunzatoare orei. Excel actualizeaza
data la fiecare activare si recalculare a foii de calcul. De exemplu, in
data de 23 septembrie 2003 aceasta functie returneaza data "9/23/2003"
in format american, sau "23-Sep-03" intr-un format european. Daca se
schimba formatul in unul general, valoarea returnata este
numarul serial 37887.
v
WEEKDAY(data_calendaristica
[, tip_calendar]) - Aceasta functie converteste o data
calendaristica in numarul zilei din saptamana,
valoarea returnata fiind intre 1 si 7. Parametrul optional tip_calendar indica ziua de
inceput a saptamanii si poate avea una din urmatoarele valori:
Valoarea 1
- Daca se foloseste aceasta valoare, prima zi din
saptamana este duminica, iar ultima zi din
saptamana este sambata. Daca parametrul
lipseste, se considera ca are valoarea 1.
Valoarea 2
- Daca se foloseste aceasta valoare, prima zi din
saptamana este luni, iar ultima zi din saptamana
este duminica.
De exemplu, functia
WEEKDAY("24-Dec-2003") returneaza valoarea 4, iar WEEKDAY("24-Dec-2003",
2) returneaza valoarea 3.
v
YEAR(data_calendaristica) - Aceasta
functie returneaza un numar care reprezinta anul din data calendaristica
transmisa ca parametru. De exemplu, functia YEAR("25-Dec-03
17:30:17") va returna valoarea 2003 care reprezinta numarul anului
din aceasta data, iar functia YEAR(37980.7293634259) va returna
aceeasi valoare 2003.
v
YEARFRAC(data_inceput,
data_sfarsit [, tip]) - Aceasta functie returneaza partea
fractionara a diferentei dintre data_sfarsit si data_inceput,
exprimata in ani. Parametrul optional tip indica tipul de an si de luna care se ia in
considerare. Acest parametru poate lua una din urmatoarele valori:
Valoarea 0 - Daca se foloseste
aceasta valoare, se considera un model american cu ani de 360 de zile
si luni de 30 de zile.
Valoarea 1 - Daca se foloseste
aceasta valoare, se considera ani calendaristici obisnuiti
si luni calendaristice obisnuite.
Valoarea 2 - Daca se foloseste
aceasta valoare, se considera ani de 360 de zile si luni
calendaristice obisnuite.
Valoarea 3 - Daca se foloseste
aceasta valoare, se considera ani de 365 de zile si luni
calendaristice obisnuite.
Valoarea 4 - Aceasta valoare se
foloseste pentru un model european cu ani de 360 de zile si luni de
30 de zile.
De exemplu, daca la
adresa A1 este data "1-6-2003", iar la adresa B1 este data "1-12-2003", functia
YEARFRAC(A1, B1) returneaza valoarea 0.5, functia YEARFRAC(A1, B1, 1)
returneaza valoarea 0.501369863, functia YEARFRAC(A1, B1, 2)
returneaza valoarea 0.508333333, functia YEARFRAC(A1, B1, 3)
returneaza valoarea 0.501369863,
iar functia YEARFRAC(A1, B1, 4) returneaza valoarea 0.5.
6.3. Functii financiare
Cele
mai importante functii financiare pe care vi le ofera Excel sunt
urmatoarele:
DB(cost, recuperare,
viata, perioada [, luna]) - Aceasta functie
calculeaza deprecierea reala a unui utilaj pe o perioada indicata, folosind metoda balantei de
depreciere fixa. Ca parametri se indica un cost initial, o valoare de recuperare, precum si durata de viata a utilajului respectiv. Parametrul optional luna reprezinta numarul
de luni din primul an, valoarea implicita a acestui parametru fiind 12.
Parametrii viata si perioada trebuie sa se
exprime in aceleasi unitati de timp (ani, luni, etc.). De
exemplu, daca un utilaj care are o durata de viata de 13
ani costa $ 200 000, iar la sfarsitul perioadei de
viata va valora $ 5 000, daca vreti sa stiti
care va fi deprecierea in anul al 7-lea al vietii sale, apelati
functia DB(200000, 5000, 13, 7) si veti obtine valoarea $
9005.27.
DDB(cost,
recuperare, viata, perioada [, factor]) - Aceasta functie
calculeaza deprecierea reala a unui utilaj pe o perioada indicata, folosind metoda balantei de
depreciere dubla. Ca parametri se indica un cost initial, o valoare de recuperare, precum si durata de viata a utilajului respectiv. Parametrul optional factor reprezinta viteza de
depreciere a balantei, valoarea implicita a acestui parametru fiind
2. Parametrii viata
si perioada trebuie
sa se exprime in aceleasi unitati de timp (ani, luni,
etc.). Daca vreti sa rezolvati problema de mai sus folosind
balanta de depreciere dubla, apelati functia DDB(200000,
5000, 13, 7) si veti obtine valoarea $11293.0
VDB(cost,
recuperare, viata, inceput, sfarsit [, factor]) - Aceasta
functie calculeaza deprecierea reala a unui utilaj pe o
perioada delimitata de inceput
si sfarsit, folosind
metoda balantei variabile de depreciere. Ca parametri se indica un cost initial, o valoare de recuperare, precum si durata de viata a utilajului respectiv.
Parametrul optional factor
viteza de depreciere a balantei, valoarea implicita a acestui
parametru fiind 2. Parametrii viata,
inceput si sfarsit trebuie sa se exprime in aceleasi
unitati de timp (ani, luni, etc.).
FV(dobanda,
nper, plata [, vp] [, tip]) - Aceasta functie calculeaza
valoarea viitoare a unei investitii, care se constituie prin
incasarea.periodica a unor sume egale cu plata, intr‑un numar nper de perioade, cu o dobanda
precizata. La inceputul operatiei se poate investi o suma
initiala vp. Parametrul
optional tip are valoarea 0
daca plata se face la sfarsitul fiecarei perioade, sau 1
daca plata se face la inceputul fiecarei perioade. Parametrii vp si tip fiind optionali, valoarea implicita a lor (daca
lipsesc) este 0. Sumele plata
si vp care se platesc, se
introduc ca valori negative. De exemplu, daca la inceputul perioadei
investiti $1700 si adaugati cate $150 la sfarsitul
fiecarei luni, considerand o dobanda medie de 7%, pentru a calcula
valoarea investitiei dupa o perioada de 3 ani (36 de luni)
folositi functia FV(0.07/12, 36, -150, -1700), care returneaza
valoarea $ 8 085.4
IPMT(dobanda,
per, nper, vp [, vv] [, tip]) - Aceasta functie calculeaza dobanda
in cazul unei investitii, pentru o perioada data per, care trebuie sa fie mai
mica decat numarul total de perioade nper. Puteti folosi aceasta functie pentru a
determina dobanda la o ipoteca pentru o perioada per din intervalul nper.
Daca parametrii vv (valoarea
viitoare, adica valoarea sumei de la sfarsitul anuitatii)
si tip (0 pentru plata la
sfarsitul perioadei si 1 pentru plata la inceputul perioadei)
lipsesc, se presupune ca au valoarea implicita 0. De exemplu,
daca faceti o ipoteca de $ 170 000 cu o dobanda de 8% pe o
perioada de 20 de ani (240 de luni), daca vreti sa
stiti ce suma veti plati pentru dobanzi dupa 7
ani si jumatate (90 de luni), apelati functia IPMT(0.8/12,
90, 240, 170000). Veti obtine valoarea ($11,332.67) in rosu,
ceea ce inseamna ca este negativa, deoarece trebuie sa fie
platita.
IRR(valori [, estimare]) - Aceasta
functie calculeaza rata interna a randamentului (internal rate
of return) pentru o serie de beneficii nete (pozitive sau negative) precizate
cu ajutorul domeniului de celule valori,
pe baza unei estimari pe care o puteti preciza prin parametrul estimare. In domeniul valori, beneficiile nete trebuie
sa fie introduse in ordine cronologica. Seria sau matricea
precizata prin domeniul valori
trebuie sa contina cel putin o schimbare de semn, in caz
contrar functia returneaza o conditie de eroare. Daca la
inceputul investitiei se plateste o suma de bani, valoarea
respectiva se introduce ca un numar negativ. Parametrul estimare este cea mai buna
evaluare pe care o puteti face pentru beneficiul final. Daca
parametrul estimare lipseste,
se considera valoarea implicita de 0.1 (adica 10%). Functia
IRR() efectueaza estimari
succesive pana in momentul cand diferenta dintre doua estimari
este mai mica decat 0.00001%. Daca parametrul estimare este prea departe de adevar, aproximatiile
succesive nu converg si functia returneaza o conditie de
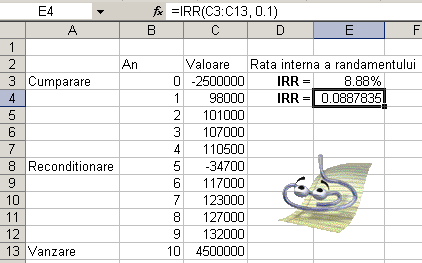
eroare. In acest caz trebuie sa modificati valoarea parametrului estimare. In tabelul figura urmatoare
este introdus pe o coloana beneficiul realizat cu ajutorul unui utilaj,
care a fost cumparat cu 2 500 000 lei, dupa 5 ani i s‑a
facut o reconditionare, apoi a fost vandut cu 4 500 000 lei. Pentru a
gasi rata interna a randamentului se introduce in celula E3 formula =IRR(C3:C13, 0.1), care returneaza
valoarea 8.88%. In celula E4 se obtine pe baza aceleiasi formule
acelasi rezultat exprimat in format general prin valoarea 0.0887835.
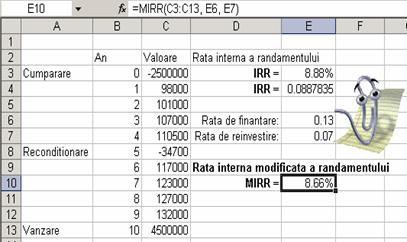
MIRR(valori,
rata_finantare, rata_reinvestire) - Aceasta functie
calculeaza rata interna modificata a randamentului (modified
internal rate of return) pentru o serie de beneficii nete (pozitive sau
negative) precizate cu ajutorul domeniului de celule valori. Parametrul rata_finantare
este costul finantarii investitiei si reprezinta
dobanda care se ia pentru banii imprumutati, necesari investitiei.
Parametrul rata_reinvestire
reprezinta rata cu care se pot reinvesti beneficiile nete pozitive intr‑un
instrument sigur, cum ar fi un CD. Seria sau matricea precizata prin domeniul
valori trebuie sa
contina cel putin o schimbare de semn, in caz contrar
functia returneaza o conditie de eroare. Pentru a vedea cum se
foloseste aceasta functie, reluati exemplul anterior
si faceti urmatoarele operatii:
Introduceti in celula E6 valoarea 0.13, care
reprezinta rata de finantare.
Introduceti in celula E7 valoarea 0.07, care
reprezinta rata de reinvestire.
Introduceti in celula E10 formula =MIRR(C3:C13,
E6, E7) pentru a calcula rata interna modificata a randamentului.
Rezultatul este 8.66, cu 0.22%
mai mic decat cel obtinut cu functia IRR(). In proiecte la care
beneficiile nete difera, sau care implica sume mari de bani,
diferenta dintre rezultatele obtinute prin cele doua
functii pot sa difere destul de mult. De obicei functia MIRR()
ofera rezultate mai apropiate de realitate.
NPER(dobanda,
plata, vp [, vv] [, tip]) - Aceasta functie calculeaza
numarul de perioade de plata necesare pentru o investitie,
pentru a realiza anuitatea in conditiile precizate prin parametri. De
exemplu, pentru a calcula numarul de perioade de plata pentru o
investitie de $ 11 000, cu o dobanda medie de 8% si o rata
de $750, apelati functia =NPER(0.8/12, ‑750, 11000). Veti
obtine valoarea 58.9828, adica 59 de perioade.
NPV(dobanda,
valori) - Aceasta functie calculeaza valoarea neta
prezenta a unei investitii, pe baza unei serii de beneficii precizate
prin sirul valoari, fiind dat
un rabat egal cu dobanda.
Sirul de valori poate fi precizat cu ajutorul unor domenii de celule, sau
printr‑o succesiune de valori constante introduse ca parametri
separati. De exemplu, sa presupunem ca ati cumparat un
utilaj cu $18 000 bani gheata (cash) cu o dobanda de 7%. In
urmatorii 6 ani utilajul va face o economie anuala respectiv de
$4000, $3000, $3000, $3000, $2000, $1500, apoi il vindeti imediat cu $10
000. Pentru a vedea daca investitia a fost rentabila,
apelati functia NPV(0.07, 4000, 3000, 3000, 3000, 2000, 11500).
Valoarea returnata de functia de mai sus este $ 20 185.12, ceea ce
inseamna ca prin investitia respectiva ati economisit
$ 2 185.12.
PMT(dobanda,
nper, vp [, vv] [, tip]) - Aceasta functie calculeaza
platile periodice care trebuie sa fie efectuate pentru o
anuitate, fiind date dobanda,
termenul nper si valoarea
prezenta vp. Daca
parametrii vv (valoarea viitoare,
adica valoarea sumei de la sfarsitul anuitatii) si tip (0 pentru plata la sfarsitul
perioadei si 1 pentru plata la inceputul perioadei) lipsesc, se presupune
ca au valoarea implicita 0. De exemplu, sa presupunem ca
vreti sa achizitionati un teren cu $ 150 000 cu plata in 20
de ani cu o dobanda de 11%. Daca vreti sa gasiti
valoarea unei plati lunare apelati functia PMT(0.11/12,
20*12, 150000). Veti obtine valoarea ($ 1 548.28) in rosu, ceea
ce inseamna ca este negativa, deoarece trebuie sa fie
platita.
Observatie. Trebuie sa aveti
grija ca parametrii care au
legatura cu perioadele de timp sa fie compatibili. De exemplu,
in functia de mai sus parametrul dobanda
se calculeaza pe luna, iar parametrul nper reprezinta numarul de luni din 20 de ani, deoarece
plata se face in rate lunare.
PPMT(dobanda,
per, nper, vp [, vv] [, tip]) - Aceasta functie calculeaza
portiunea principala a unei plati care este
facuta pentru o investitie amortizata. Aceasta
portiune este acea parte din valoarea returnata de PMT(), care reduce
echilibrul unei balante. Daca parametrii vv (valoarea viitoare, adica valoarea sumei de la
sfarsitul anuitatii) si tip (0 pentru plata la sfarsitul perioadei si 1 pentru
plata la inceputul perioadei) lipsesc, se presupune ca au valoarea
implicita egala cu 0. Daca reluam exemplul anterior, plata
principala efectuata in luna a douasprezecea este data de
functia PPMT(0.11/12, 12, 20*12, 150000). Veti obtine valoarea
($191.58) in rosu, ceea ce inseamna ca este negativa,
deoarece trebuie sa fie platita.
PV(dobanda,
nper, plata [, vv] [, tip]) - Aceasta functie calculeaza
valoarea prezenta (Present Value) a unei investitii, care este constituita prin plati egale
cu plata timp de nper perioade, cu o dobanda constanta. Daca
parametrii vv (valoarea viitoare,
adica valoarea sumei de la sfarsitul anuitatii) si tip (0 pentru plata la sfarsitul
perioadei si 1 pentru plata la inceputul perioadei) lipsesc, se presupune
ca au valoarea implicita egala cu 0. De exemplu, sa
presupunem ca vreti sa cumparati o vila pentru
care va puteti permite sa platiti in fiecare luna
$800 timp de 20 de ani. Daca imprumuturile se fac cu o dobanda de
10%, cat de mare este imprumutul pe care il puteti face pentru a
plati vila ? Raspunsul la aceasta intrebare il
obtineti prin functia PV(0.1/12, 20*12, -800), care
returneaza imediat rezultatul $ 82 896 Parametrul plata este o valoare negativa, deoarece reprezinta
rata lunara care trebuie sa fie platita.
RATE(nper,
plata, vp [, vv] [, tip] [, estimare]) - Aceasta functie
calculeaza rata dobanzii pentru perioada unei anuitati, pe baza
parametrilor precizati. Daca parametrii vv (valoarea viitoare, adica valoarea sumei de la
sfarsitul anuitatii) si tip (0 pentru plata la sfarsitul perioadei si 1 pentru
plata la inceputul perioadei) lipsesc, se presupune ca au valoarea
implicita egala cu 0. Parametrul estimare
este cea mai buna evaluare pe care o puteti face pentru rata
dobanzii. Daca parametrul estimare lipseste, se considera
valoarea implicita de 0.1 (adica 10%). Puteti obtine
rezultate diferite in functie de valoarea pe care o folositi ca estimare. Daca estimarea este prea
departe de o valoare reala, functia returneaza o conditie
de eroare. De exemplu, =RATE(12,-900,10000) returneaza o rata a
dobanzii de 1% pe luna (12% pe an). Daca alegeti un format
general pentru valoarea respectiva, obtineti 0.012043457.
SLN(cost,
valorificare, durata) - Aceasta functie calculeaza valoarea
deprecierii anuale a unui utilaj (Straight-LiNe depreciation), fiind dat un cost initial, o valorificare de la sfarsitul
ciclului de viata economica si o durata de viata economica. De exemplu, prin
apelul functiei =SLN(20000, 7000, 4) obtineti o valoare de
depreciere egala cu $ 3 250.00 pe an.
SYD(cost,
valorificare, durata, perioada) - Aceasta functie
calculeaza valoarea deprecierii pentru o perioada data, folosind asa numita metoda de
insumare a anilor (Sum‑of‑Years' Digits). Trebuie sa se
precizeze un cost initial, o valorificare de la sfarsitul
ciclului de viata economica si durata de viata economica. De exemplu, formula =SYD(20000,
7000, 4, 1) calculeaza o depreciere de $5200.00 pentru primul an, formula
=SYD(20000, 7000, 4, 2) calculeaza o depreciere de $3900.00 pentru al
doilea an, iar formula =SYD(20000, 7000, 4, 3) calculeaza o depreciere de
$2600.00 pentru al treilea an.
VDB(cost,
valorificare, durata, inceput, sfarsit [, factor] [, comut]) - Aceasta
functie calculeaza valoarea deprecierii unei proprietati pe
perioada dintre inceput si sfarsit, folosind metoda
balantei in declin (Variable Declining Balance). Parametrii cost, valorificare si durata au aceeasi
semnificatie ca la functiile anterioare. Parametrii inceput, sfarsit si durata trebuie sa fie
exprimati in aceleasi unitati de timp. Parametrul
optional factor reprezinta
rata cu care se depreciaza balanta, valoarea implicita a sa
fiind egala cu 2. Parametrul optional comut poate avea una din valorile logice FALSE (valoarea
implicita) sau TRUE, si permite sa se faca trecerea la o
depreciere liniara, daca deprecierea este mai mare decat cea
rezultata din factorul de declin. Daca parametrul are valoarea FALSE,
sau daca lipseste, se face trecerea la deprecierea liniara.
Daca parametrul are valoarea TRUE, se evita trecerea la deprecierea
liniara.
6.4. Functii matematice
Cele
mai importante functii matematice pe care vi le ofera Excel sunt
urmatoarele:
v
ABS(numar) - Aceasta
functie calculeaza valoarea absoluta a numarului precizat
ca parametru.
v
CEILING(numar,
semnificatie) - Aceasta functie calculeaza valoarea rotunjita in
sus a unui numar pana la
cel mai apropiat multiplu de semnificatie.
Daca cei doi parametri nu au acelasi semn, se returneaza o
valoare de eroare. De exemplu functia =CEILING(7.12, 0.5) returneaza
valoarea 7.5, iar =CEILING(-7.12, -0.5) returneaza valoarea -7.5.
v
COMBIN(n, k) - Aceasta
functie calculeaza valoarea care este cunoscuta din liceu ca
si "combinari de n luate
cate k". De exemplu, functia
COMBIN(7, 3) returneaza valoarea 35 (adica 7*6*5/1*2*3).
v
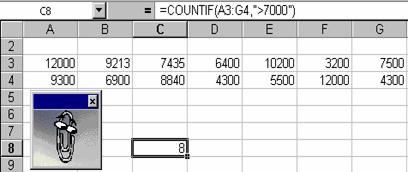
COUNTIF(domeniu,
criteriu) - Aceasta functie
numara celulele dintr‑un domeniu, care satisfac un criteriu. De
exemplu, daca in domeniul A3:G4 ati introdus vanzarile realizate
in diferite puncte de desfacere si vreti sa vedeti in cate
puncte valoarea vanzarilor este mai mare decat 7000, apelati
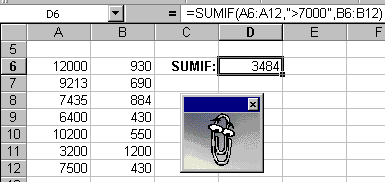
functia =COUNTIF(A3:G4,'>7000') ca in figura de mai jos.
v
EVEN(numar) - Aceasta
functie rotunjeste un numar
in sus, pana la cel mai apropiat numar par (cu sot). De exemplu
functia EVEN(7.1) returneaza o valoare egala cu 8, iar EVEN(-7)
returneaza -8.
v
EXP(x) - Aceasta
functie calculeaza valoarea exponentiala ex pentru parametrul x, unde e este baza logaritmilor naturali (valoarea lui e este aproximativ
egala cu 2.71828182845905).
v
FACT(n) - Aceasta
functie calculeaza valoarea n!,
care se numeste factorialul
numarului n, aceasta valoare fiind egala cu produsul
1*2*3* . *n.
v
FLOOR(numar,
semnificatie) - Aceasta functie calculeaza valoarea rotunjita in
jos a unui numar pana la
cel mai apropiat multiplu de semnificatie.
Daca cei doi parametri nu au acelasi semn, se returneaza o
valoare de eroare. De exemplu functia =FLOOR(7.12, 0.5) returneaza
valoarea 7, iar =FLOOR(-7.12, -0.5) returneaza valoarea -7.
v
INT(numar) - Aceasta
functie rotunjeste un numar
pana la cel mai apropiat numar intreg. De exemplu functia
=INT(7.12) returneaza valoarea 7, iar functia =INT(‑7.12)
returneaza valoarea -8.
v
LN(x) - Aceasta
functie calculeaza valoarea logaritmului natural (in baza e, care are valoarea aproximativ egala
cu 2.71828182845905) pentru parametrul x.
Parametrul x trebuie sa fie
pozitiv.
v
LOG(x, [a]) - Aceasta
functie calculeaza valoarea logaritmului in baza a din x (care se
noteaza logax). Parametrul x trebuie sa fie pozitiv.
Daca parametrul a (care este
optional) lipseste, se considera ca este egal cu 10 (baza
logaritmilor zecimali).
v
LOG10(x) - Aceasta
functie calculeaza valoarea logaritmului zecimal (in baza 10) pentru parametrul x. Parametrul x trebuie sa fie pozitiv.
v
MDETERM(matrice) - Aceasta
functie calculeaza valoarea determinantului unei matrice patrate. Parametrul matrice poate fi un domeniu de celule, sau un sir de valori.
v
MINVERSE(matrice) - Aceasta
functie calculeaza inversa unei matrice
patrate. Parametrul matrice
poate fi un domeniu de celule, sau un sir de valori. Intrucat rezultatul
acestei functii este o matrice,
trebuie sa introduceti functia MINVERSE() ca o formula de tip matrice. Pentru a
face acest lucru, selectati domeniul receptor pentru rezultat (adica
pentru matricea inversa), introduceti formula =MINVERSE(matrice),
apoi validati formula prin combinatia de taste Shift+Ctrl+Enter.
v
MMULT(matrice1,
matrice2) - Aceasta functie calculeaza produsul dintre matrice1 si matrice2. Parametrii pot fi domenii de celule, sau siruri de
valori. Numarul de coloane din matrice1
trebuie sa fie egal cu numarul de linii din matrice2. Intrucat rezultatul acestei functii este o matrice, trebuie sa introduceti
functia MINVERSE() ca o formula
de tip matrice, asa cum s‑a explicat la functia MINVERSE().
v
MOD(numar,
divizor) - Aceasta functie calculeaza modulul unui numar relativ la un divizor (adica restul
impartirii acelui numar
la divizor).
v
ODD(numar) - Aceasta
functie rotunjeste un numar
in sus, pana la cel mai apropiat numar impar (fara
sot). De exemplu functia EVEN(7.1) returneaza o valoare
egala cu 9, iar EVEN(-7) returneaza -7.
v
PI() - Aceasta
functie returneaza valoarea constantei p, a carei valoare este
egala aproximativ cu 3.1415926535897
v
POWER(n, p) - Aceasta
functie calculeaza valoarea np
(adica n la puterea p).
v
PRODUCT(numere) - Aceasta
functie calculeaza produsul unor numere
precizate ca parametri. Puteti introduce pana la 30 de parametri, care
pot fi constante, sau adresele unor domenii de celule care contin numerele.
v
RAND() - Aceasta
functie calculeaza un numar
aleator intre 0 si 1. La fiecare recalculare a foii de calcul, vor fi
generate alte numere. Pentru a provoca recalcularea foii de calcul, puteti
folosi tasta F Daca vreti sa obtineti un numar
aleator intre 0 si n, folositi formula =RAND()*n. Daca
vreti ca numarul aleator sa fie intreg, alegeti un format
numeric fara zecimale.
v
ROMAN(numar [, format])
) -
Aceasta functie converteste un numar arab in numar roman, sub forma de text.
Parametrul optional format
poate avea una din valorile 0 (valoare implicita), 1, 2, 3, 4, TRUE, sau FALSE,
avand ca efect folosirea unor conventii particulare pentru obtinerea
unor forme mai concise, sau mai simple, a unor numere romane. De exemplu,
ROMAN(499) returneaza valoarea "CDXCIX", ROMAN(499, 1) returneaza
valoarea "LDVLIV", ROMAN(499, 2) returneaza valoarea "XDIX", ROMAN(499, 3)
returneaza valoarea "VDIV", iar ROMAN(499, 4) returneaza valoarea
"ID".
v
ROUND(numar,
num_poz) - Aceasta functie rotunjeste un numar la un numar de pozitii precizat prin num_poz. Daca num_poz este pozitiv se face rotunjirea la dreapta marcii
zecimale, daca num_poz este
egal cu zero se face rotunjirea la un numar intreg, iar daca num_poz este negativ se face rotunjirea
la stanga marcii zecimale. De exemplu functia =ROUND(17.25, 1)
returneaza valoarea 17.3, iar functia =ROUND(17.25, -1)
returneaza valoarea 20.
v
ROUNDUP(numar,
num_poz) - Aceasta functie rotunjeste in sus un numar la un numar de
pozitii precizat prin num_poz.
Daca num_poz este pozitiv se
face rotunjirea la dreapta marcii zecimale, daca num_poz este egal cu zero se face rotunjirea la un numar
intreg, iar daca num_poz este
negativ se face rotunjirea la stanga marcii zecimale. De exemplu,
functia =ROUNDUP(17.27, 0) returneaza valoarea 18, iar functia
=ROUNDUP(17.27, 1) returneaza valoarea 17.3.
v
ROUNDDOWN(numar,
num_poz) - Aceasta functie rotunjeste in jos un numar la un numar de
pozitii precizat prin num_poz.
Daca num_poz este pozitiv se
face rotunjirea la dreapta marcii zecimale, daca num_poz este egal cu zero se face rotunjirea la un numar
intreg, iar daca num_poz este
negativ se face rotunjirea la stanga marcii zecimale. De exemplu,
functia din formula =ROUNDDOWN(17.27, 0) returneaza valoarea 17, iar
functia =ROUNDDOWN(17.27, 1) returneaza valoarea 17.2.
v
SIGN(numar) - Aceasta
functie returneaza semnul unui numar,
adica +1 daca numarul este pozitiv, 0 daca numarul
este nul si -1 daca numarul este negativ.
v
SQRT(numar) - Aceasta
functie returneaza o valoare egala cu radacina patrata (square root) din parametrul numar.
v
SUM(numere) - Aceasta
functie calculeaza suma unor numere
precizate ca parametri. Puteti introduce pana la 30 de parametri, care
pot fi constante, sau adresele unor domenii de celule care contin
numerele.
v
SUMIF(domeniu,
criteriu [, dom_insumare]) - Aceasta functie calculeaza suma
unor numere dintr‑un domeniu de celule, pe baza unui anumit criteriu. Datele din domeniu sunt evaluate pentru a se vedea
daca indeplinesc criteriul. Sunt insumate datele corespondente din dom_insumare daca este prezent
acest parametru, iar daca este absent se insumeaza datele din domeniu. In figura de mai jos este dat
un exemplu.
v
SUMPRODUCT(matrice1,
matrice2 [, matrice3], . ) - Aceasta functie efectueaza produsul
elementelor corespondente din matricele precizate ca parametri, apoi
insumeaza produsele respective. Toate matricele trebuie sa aiba
aceleasi dimensiuni. Numarul matricelor specificate ca parametri
poate fi intre 2 si 30.
v
SUMSQ(numere) - Aceasta
functie calculeaza suma patratelor unor numere precizate ca parametri. Puteti introduce pana la
30 de parametri, care pot fi constante, sau adresele unor domenii de celule
care contin numerele.
v
SUMX2MY2(matrice1,
matrice2) - Aceasta functie calculeaza suma diferentelor
patratelor valorilor corespondente din cele doua matrice precizate ca
parametri. Cele doua matrice trebuie sa fie de dimensiuni egale.
v
SUMX2PY2(matrice1,
matrice2) - Aceasta functie calculeaza suma sumelor
patratelor valorilor corespondente din cele doua matrice precizate ca
parametri. Cele doua matrice trebuie sa fie de dimensiuni egale.
v
TRUNC(numar,
num_poz) - Aceasta functie trunchiaza un numar la un numar de pozitii precizat prin num_poz. Daca num_poz este pozitiv se face trunchierea la dreapta marcii
zecimale, daca num_poz este
egal cu zero se face trunchierea la un numar intreg, iar daca num_poz este negativ se face
trunchierea la stanga marcii zecimale. De exemplu, apelul functiei
=TRUNC(17.77, 0) returneaza valoarea 17, apelul functiei
=TRUNC(17.77, 1) returneaza valoarea 17.7, iar apelul functiei
=TRUNC(17.77, -1) returneaza valoarea 10.
6.5. Functii trigonometrice
O
subclasa a functiilor matematice pe care vi le ofera Excel sunt functiile trigonometrice. Aceste functii
trigonometrice au ca parametri niste unghiuri,
care se pot exprima in grade, sau radiani. Pentru conversia unghiurilor
din grade in radiani si invers, puteti folosi urmatoarele
functii:
v
RADIANS(unghi) - converteste
in radiani un unghi exprimat in grade.
De exemplu, RADIANS(270) returneaza valoarea 4.712389, care
reprezinta de fapt 3p/2 radiani.
v
DEGREES(unghi) - converteste
in grade un unghi exprimat in
radiani. De exemplu, RADIANS(PI()/2) returneaza valoarea 90, deoarece un
unghi de p/2 radiani are 90 de
grade.
Functiile trigonometrice directe pe
care vi le ofera Excel sunt urmatoarele:
v
SIN(unghi) - returneaza
valoarea functiei sinus pentru
un unghi exprimat in radiani. De
exemplu, =SIN(PI()/6) returneaza valoarea 0.5. Daca aveti
unghiul exprimat in grade, trebuie sa folositi functia RADIANS,
sau sa inmultiti valoarea cu PI()/180, pentru a o transforma in
radiani. De exemplu, pentru a calcula sinus de
60 de grade se poate folosi formula =SIN(RADIANS(60)), sau formula
=SIN(60*PI()/180). In ambele cazuri veti obtine valoarea 0.866025404,
care este aproximativ egala cu SQRT(3)/2. Daca vreti sa
calculati sinus de p radiani (180 de
grade), folositi formula =SIN(PI()) si veti obtine o
valoare aproximativ egala cu 0 (de fapt veti obtine o valoare
exponentiala foarte mica, de exemplu 1.22515E-16, care este
practic egala cu zero)
v
COS(unghi) - returneaza
valoarea functiei cosinus pentru
un unghi exprimat in radiani. De
exemplu, =COS(PI()/6) returneaza valoarea 0.866025404, care este
aproximativ egala cu SQRT(3)/2. Pentru a calcula cosinus de 60 de grade se poate folosi formula
=COS(RADIANS(60)), sau formula =COS(60*PI()/180). In ambele cazuri veti
obtine valoarea 0.5.
v
TAN(unghi) - returneaza
valoarea functiei tangenta
pentru un unghi exprimat in radiani.
De exemplu, =TAN(PI()/6) returneaza valoarea 0.577350269, care este
aproximativ egala cu SQRT(3)/3. Pentru a calcula tangenta de 60 de grade se poate folosi formula
=TAN(RADIANS(60)), sau formula =TAN(60*PI()/180). In ambele cazuri veti
obtine valoarea 1.7320508, care este aproximativ egala cu SQRT(3).
Functiile trigonometrice inverse pe care vi le
ofera Excel sunt urmatoarele:
v
ASIN(numar) - este inversa
functiei sinus si
returneaza valoarea unui unghi pentru care SIN(unghi) = numar. Prin urmare, parametrul numar trebuie sa
apartina internalului [-1, 1].
Valoarea returnata se exprima in radiani si apartine
intervalului [-p p/2]. Daca vreti
sa obtineti rezultatul in grade, aplicati valorii
obtinute functia DEGREES. De exemplu, =ASIN(0.5) returneaza
valoarea 0.52359878, care este aproximativ egala cu p/6 (exprimata in
radiani), iar =DEGREES(ASIN(0.5)) returneaza valoarea 30 (exprimata
in grade).
v
ACOS(numar) - este inversa
functiei cosinus si
returneaza valoarea unui unghi pentru care COS(unghi) = numar. Prin urmare, parametrul numar trebuie sa
apartina internalului [-1, 1].
Valoarea returnata se exprima in radiani si apartine
intervalului [0, p]. Daca
vreti sa obtineti rezultatul in grade, aplicati
valorii obtinute functia DEGREES. De exemplu, =ACOS(0.5) returneaza
valoarea 1.047197551, care este aproximativ egala cu p/3 (exprimata in
radiani), iar =DEGREES(ACOS(0.5)) returneaza valoarea 60 (exprimata
in grade).
v
ATAN(numar) - este inversa
functiei tangenta si
returneaza valoarea unui unghi pentru care TAN(unghi) = numar. Valoarea returnata se
exprima in radiani si apartine intervalului [-p p/2]. Daca vreti
sa obtineti rezultatul in grade, aplicati valorii
obtinute functia DEGREES. De exemplu, =ATAN(1) returneaza
valoarea 0.785398, care este aproximativ egala cu p/4 (exprimata in
radiani), iar =DEGREES(ATAN(1)) returneaza valoarea 45 (exprimata in
grade).
6.6. Functii statistice
Excel are o
multime de functii statistice care va ajuta in rezolvarea
unor probleme clasice de analiza statistica. Cele mai importante
functii statistice pe care vi le ofera Excel sunt
urmatoarele:
AVERAGE(numere) - Aceasta
functie calculeaza media
aritmetica unor numere
precizate ca parametri. Puteti introduce pana la 30 de parametri, care
pot fi constante, sau adresele unor domenii de celule care contin numerele
pentru care vreti sa calculati media aritmetica.
COUNT(parametri) - Aceasta
functie calculeaza numarul valorilor
numerice cuprinse in parametri.
Puteti introduce pana la 30 de parametri, care pot fi constante, sau
adresele unor domenii de celule care contin valorile pe care vreti
sa le numarati.
COUNTA(valori) - Aceasta
functie calculeaza numarul valorilor
de orice tip cuprinse in parametri.
Puteti introduce pana la 30 de parametri, care pot fi constante, sau
adresele unor domenii de celule care contin valorile pe care vreti
sa le numarati.
GROWTH(y_cunosc [, x_cunosc]
[, x_noi] [, const]) - Aceasta functie calculeaza
cresterile exponentiale ale unor valori y corespunzatoare valorilor din domeniul x_noi, cunoscand perechile de valori din domeniile y_cunosc si x_cunosc. Daca x_cunosc
lipseste, se considera un sir al numerelor naturale
de dimensiune egala cu cea a domeniului y_cunosc. Este determinata functia exponentiala
y = b*ax care
exprima cel mai bine relatia dintre y si x. Daca const este TRUE (sau daca
lipseste), se determina si parametrul b, iar daca const
este FALSE, se determina numai parametrul a, valoarea lui b fiind
considerata egala cu 1 (in acest caz relatia este y = ax). Intrucat rezultatul
acestei functii este o matrice,
trebuie sa introduceti functia GROWTH() ca o formula de tip matrice, asa
cum s‑a explicat la functia MINVERSE().
LINEST(y_cunosc [, x_cunosc]
[, const] [, stat]) - Aceasta functie determina o
functie liniara de tipul y =
a*x + b care se potriveste cel mai bine cu perechile de valori din
domeniile y_cunosc si x_cunosc. Daca x_cunosc lipseste, se
considera un sir al numerelor naturale de dimensiune
egala cu cea a domeniului y_cunosc.
Daca const este TRUE (sau
daca lipseste), se determina si parametrul b, iar daca const este FALSE, se determina numai parametrul a, valoarea lui b fiind considerata egala cu 0 (relatia este y = a*x). Daca parametrul stat este TRUE, se afisaza
urmatorii parametri statistici:
Eroarea standard pentru parametrul a;
Eroarea standard pentru parametrul b;
Coeficientul de determinare (sau de corelatie)
dintre valorile estimate si cele cunoscute pentru variabila y;
Eroarea standard pentru estimarile variabilei y;
Parametrul F
care compara dispersiile, pentru a vedea daca relatia dintre x si y este intamplatoare, sau nu.
Parametrul statistic df (degrees of freedom), care determina numarul gradelor
de libertate;
Regresia sumei patratelor;
Suma reziduala a patratelor.
LOGEST(y_cunosc,
[x_cunosc] [,const] [,stat]) - Aceasta functie determina o
functie exponentiala de tipul y = b*ax care se potriveste cel mai bine cu
perechile de valori din domeniile y_cunosc
si x_cunosc. Daca x_cunosc lipseste, se
considera un sir al numerelor naturale de dimensiune egala
cu cea a domeniului y_cunosc.
Daca const este TRUE (sau
daca lipseste), se determina si parametrul b, iar daca const este FALSE, se determina numai parametrul a, valoarea lui b fiind considerata egala cu 1 (in acest caz relatia
este y = ax). Daca
parametrul stat este TRUE, se
afisaza urmatorii parametri statistici:
Eroarea standard pentru parametrul a;
Eroarea standard pentru parametrul b;
Coeficientul de determinare (sau de corelatie)
dintre valorile estimate si cele cunoscute pentru variabila y;
Eroarea standard pentru estimarile variabilei y;
Parametrul F
care compara dispersiile, pentru a vedea daca relatia dintre x si y este intamplatoare, sau nu.
Parametrul statistic df (degrees of freedom), care determina numarul gradelor
de libertate;
Regresia sumei patratelor;
Suma reziduala a patratelor.
MAX(numere) - Aceasta
functie returneaza cel mai mare dintr‑un sir de numere precizate ca parametri.
Puteti introduce pana la 30 de parametri, care pot fi constante, sau
adresele unor domenii de celule care contin numerele pentru care
vreti sa calculati valoarea maxima.
MEDIAN(numere) - Aceasta
functie returneaza mediana
(valoarea din mijloc) a unui sir de numere.
Daca sirul contine un numar par de elemente, mediana este egala cu media
aritmetica a celor doua elemente din mijloc. Puteti introduce
pana la 30 de parametri, care pot fi constante, sau adresele unor domenii
de celule care contin numerele pentru care vreti sa
calculati valoarea mediana.
MIN(numere) - Aceasta
functie returneaza cel mai mic dintr‑un sir de numere precizate ca parametri.
Puteti introduce pana la 30 de parametri, care pot fi constante, sau
adresele unor domenii de celule care contin numerele pentru care
vreti sa calculati valoarea minima.
STDEV(numere) - Aceasta
functie calculeaza abaterea standard
(standard deviation) a unei populatii pe baza unui esantion numere precizate ca parametri.
Puteti introduce pana la 30 de parametri, care pot fi constante, sau
adresele unor domenii de celule care contin numerele pentru care
vreti sa calculati abaterea standard.
STDEVP(numere) - Aceasta
functie calculeaza abaterea
standard (standard deviation) a unei populatii, cand toate elementele
populatiei sunt incluse in parametrii numere.
Puteti introduce pana la 30 de parametri, care pot fi constante, sau
adresele unor domenii de celule care contin numerele pentru care
vreti sa calculati abaterea standard relativa la intreaga
populatie.
TREND(y_cunosc [, x_cunosc]
[, x_noi] [, const]) - Aceasta functie calculeaza
tendinta liniara ale unor valori y
corespunzatoare valorilor din domeniul x_noi, cunoscand perechile de valori din domeniile y_cunosc si x_cunosc. Daca x_cunosc
lipseste, se considera un sir al numerelor naturale
de dimensiune egala cu cea a sirului din y_cunosc. Este determinata o functie liniara de
tipul y = a*x + b care exprima cel mai bine relatia dintre y si x. Daca const este
TRUE (sau daca lipseste), se determina si parametrul b, iar daca const este FALSE, se determina numai parametrul a, valoarea lui b fiind considerata egala cu 0 (in acest caz relatia
este y = a*x). Intrucat rezultatul
acestei functii este o matrice,
trebuie sa introduceti functia GROWTH() ca o formula de tip matrice, asa
cum s‑a explicat la functia MINVERSE().
VAR(numere) - Aceasta
functie calculeaza dispersia
sau varianta (variance) unei
populatii pe baza unui esantion numere
precizate ca parametri. Puteti introduce pana la 30 de parametri, care
pot fi constante, sau adresele unor domenii de celule care contin numerele
pentru care vreti sa calculati dispersia.
VARP(numere) - Aceasta
functie calculeaza dispersia
sau varianta (variance) unei
populatii, cand toate elementele populatiei sunt incluse in
parametrii numere. Puteti introduce pana la 30 de parametri, care pot
fi constante, sau adresele unor domenii de celule care contin numerele
pentru care vreti sa calculati dispersia relativa la
intreaga populatie.
Observatie
Excel are zeci de functii pentru toate domeniile si
pentru orice categorie de aplicatii. Spatiul acestei carti
este prea mic pentru a descrie toate aceste functii. Pentru a obtine
explicatii relative la o functie, apelati comanda Help | Contents and Index.
Calculul tendintelor cu ajutorul functiilor
Excel are anumite functii de extrapolare
care permit calculul functiei optime pentru cresterea liniara
sau exponentiala a unei curbe care trece prin anumite puncte. Aceste functii sunt urmatoarele:
LINEST() - calculeaza
parametrii pentru functia de interpolare liniara y = ax + b;
LOGEST() - calculeaza
parametrii pentru functia de interpolare exponentiala
y = b ax;
TREND() - calculeaza
valorile de-a lungul dreptei de crestere liniara (prognoza pe
termen scurt);
GROWTH() - calculeaza
valorile de-a lungul curbei de crestere exponentiala
(prognoza pe termen scurt).
Daca
vreti sa faceti o prognoza asupra cresterii liniare a
profitului pe anii 2004 si 2005 in functie de profitul realizat in
perioada 1999-2003, puteti folosi functia TREND() in felul
urmator:
Creati o foaie de
calcul noua in care introduceti in domeniul A4:A10 seria anilor 1999‑2005,
iar in domeniul B4:B8 profitul realizat in anii 1999-2003;
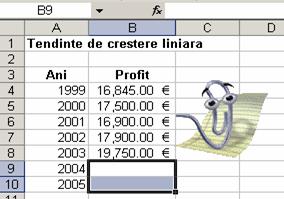
Selectati domeniul
B9:B10 in care urmeaza sa obtineti valorile pentru anii 2004
si 2005, pe baza tendintei de crestere liniara;
Introduceti formula =TREND(B4:B8, A4:A8, A9:A10), unde
parametrii au urmatoarea semnificatie:
B4:B8 - valorile cunoscute pe axa Oy, adica
valorile profitului realizat in anii 1999-2003;
A4:A8 - valorile cunoscute pe axa Ox, adica
anii 1999-2003.
A9:A10 - valorile noi de pe axa Ox, adica anii 2004-2005
pentru care doriti sa faceti prognoza pe termen scurt.
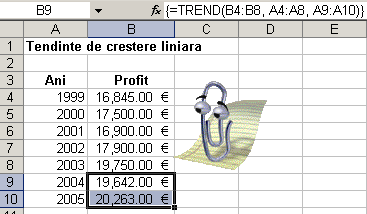
Formula pe care ati
introdus‑o este o formula
matriceala, deoarece a fost introdusa intr-un domeniu de celule (domeniul
B9:B10). Validati aceasta formula cu Shift + Ctrl + Enter;
Observatii
- In domeniul B9:B10 ati obtinut
tendinta de crestere liniata a profitului pentru anii 2004
si 2005. In linia de introducere observati formula matriceala pe care ati introdus‑o in
domeniul B9:B10. Daca vreti sa vedeti tendinta de
crestere exponentiala, urmati procedura de mai sus in
care inlocuiti functia TREND() cu functia GROWTH().
- Daca in pasul 3 al procedurii de mai
sus modificati parametrul al treilea si introduceti formula
=TREND(B4:B8, A4:A8, A4:A10),
vor fi ajustate si datele corespunzatoare anilor 1999-2003.