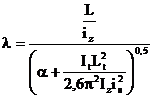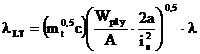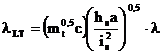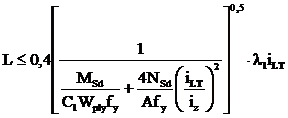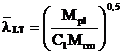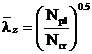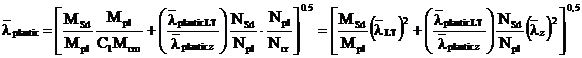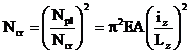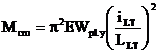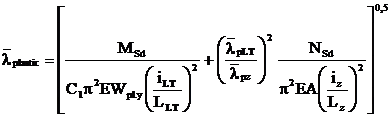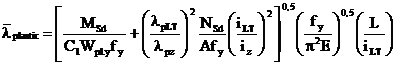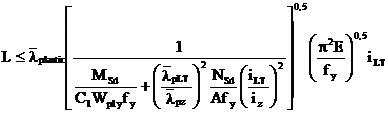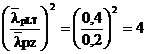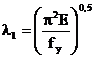Pierderea stabilitatii laterale a grinzilor
F.1 Momentul critic elastic
Momentul critic elastic pentru pierderea
stabilitatii laterale a unei grinzi cu sectiune constanta si simetrica avand talpile egale, cu legaturi de tip
standard la ambele extremitati si la care incarcarea actioneaza in planul
vertical ce trece prin centrul de forfecare al sectiunii rezulta din urmatoarea
relatie:
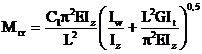
unde:
C1 se obtine din Anexa F, tabelul
F1.1 si F1.2 din EUROCODE 3 ENV 1993-1-1 pentru k=1,0
It este momentul de rasucire
libera al sectiunii transversale
Iw este momentul de rasucire
impiedicata a sectiunii transversale
Iz este momentul de inertie al
sectiunii transversale dupa axa minima de inertie
L este dinstnta dintre punctele de prindere
laterala a grinzii
Conditiile standard de prindere la extremitatile grinzii sunt
urmatoarele:
Impiedica deplasarea
laterala a sectiunii transversale
Impiedica rotirea
sectiunii transversale in jurul axei longitudinale a grinzii
Permit rotirea
sectiunii grinzii in plan orizontal
Pentru informatii suplimentare in legatura cu aceste aspecte, vezi
Anexa F a ENV 1993-1-1
F.2 Zveltetea grinzii
Generalitati
Zveltetea relativa redusa 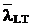 a grinzii, utilizata
in calculul de pierdere a stabilitatii laterale rezulta din urmatoarea formula:
a grinzii, utilizata
in calculul de pierdere a stabilitatii laterale rezulta din urmatoarea formula:
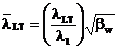
unde:
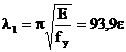
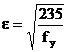 (unde fy
se exprima in N/mm2)
(unde fy
se exprima in N/mm2)
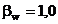 pentru sectiuni
transversale de Clasa 1 sau de Clasa 2
pentru sectiuni
transversale de Clasa 1 sau de Clasa 2
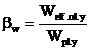 pentru sectiuni eficace de Clasa 2 (conform Anexei E)
pentru sectiuni eficace de Clasa 2 (conform Anexei E)
NOTA: In conformitate cu prevederile EUROCODE 4, daca
inima sectiunii transversale (si deci sectiunea transversala in sine) este de
Clasa 3, ea poate fi tratata ca o sectiune eficace de Clasa 2 considerand zona
centrala a portiunii comprimate a inimii ca scoasa din lucru. Zona activa pe
inaltimea comprimata a inimii de grosime "t" se considera formata din doua
portiuni de lungime 20t dispuse adiacent talpii comprimate respectiv adiacent
axei neutre a sectiunii.
Zveltetea redusa
(lLT ) a grinzii utilizata in calculul de
pierdere a stabilitatii laterale se obtine, indiferent de clasa sectiunii
transversale, din formula:
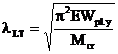
Sectiuni transversale simetrice dupa ambele axe
In cazul
grinzilor cu sectiune simetrica dupa ambele axe, in cazurile de incarcare cu
moment ccentrul de forfecare al sectiunii transversale, daca grinda nu are
extremitati fixe, valoarea (lLT ) rezulta din formula:
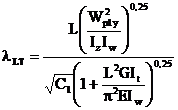
care se mai poate
scrie si sub forma urmatoare:
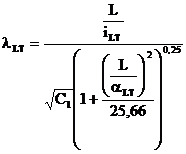
unde :
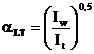
Pentru o sectiune
transversala I sau H de inaltime "h" si cu grosimea talpii tf fara
reborduri la extremitatile talpilor:
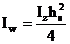
cu: 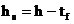
Pentru o sectiune
simetrica dupa ambele axe, valoarea (iLT) rezulta din relatia:
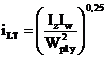
sau in forma
simplificata (cu o mica aproximare):
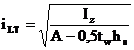
unde s-a notat cu
"tw" grosimea inimii grinzii.
Aproximatii ale zveltetii reduse utilizate in cazul
sectiunilor I sau H laminate
Pentru grinzi cu
sectiuni I sau H laminate simetrice dupa ambele axe, solicitate prin momente
concentrate aplicate la extremitati sau prin forte concentrate aplicate in
planul vertical ce trece prin centrul de forfecare al sectiunii transversale,
se poate utiliza urmatoarea formula aproximatixa acoperitoare pentru calculul
zveltetii reduse:
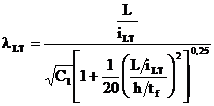
sau:
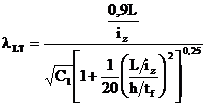
Aproximatii ale zveltetii reduse pentru alte tipuri de
sectiuni I sau H
Pentru grinzi cu
sectiune transversala I sau H de orice tip, simetrica dupa ambele axe si care
nu prezinta reborduri la extremitatile talpilor, incarcate cu momente
concentrate aplicate la extremitati sau cu forte concentrate aplicate in planul
vertical ce trece prin centrul de forfecare al sectiunii, fara fixari la
extremitati, se poate utiliza urmatoarea formula acoperitoare pentru calculul
zveltetii reduse:
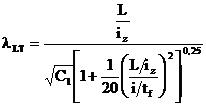
F.3 Pierderea stabilitatii laterale a barelor
incastrate la extremitati, avand talpa comprimata nelegata
F.3.1Generalitati
Aceasta sectiune
se ocupa de pierderea stabilitatii laterale a elementelor metalice sau a
portiunilor de elemente metalice cu incastrari la extremitati din punct de
vedere al rasucirii, la care talpa intinsa este legata in puncte intermediare
insa talpa comprimata este libera. (vezi Fig. F1)
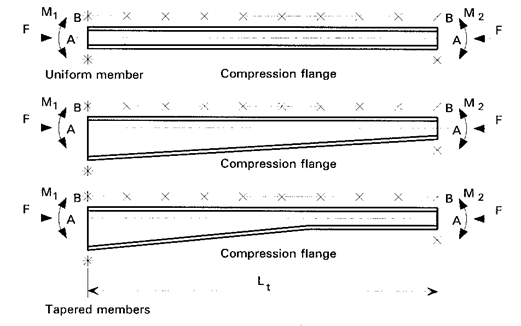
Figura
F1 - Bare incastrate la extremitati cu o talpa nelegata
Legenda:
*
= Reazeme incastrate pentru rasucire la
nivelul ambelor talpi
X
= Legaturi laterale dispuse la talpa intinsa
F
= Forta axiala (acolo unde exista)
M
= Moment concentrat direct aplicat (in ambele sensuri)
A-A
= Axa de referinta
B-B
= Axa elementelor de prindere laterala
Lt
= Lungimea libera corespunzatoare
ENV 1993-1-1 cere
sa se prevada legaturi laterale atat la talpa intinsa cat si la talpa
comprimata in zonele de aparitie a articulatiilor plastice sau daca acest lucru
nu este posibil cel putin la distanta D/2 de pozitia articulatiei plastice unde
prin "D" s-a notat inaltimea sectiunii transversale a elementului. Prinderea
este obligatorie pentru toate articulatiile in care apare rotire la valori ale
incarcarii aferente starii limita ultime, inclusiv articulatii care se
formeaza, se rotesc si apoi se opresc din rotire o data cu dezvoltarea altor
articulatii plastice.
In zonele
invecinate articulatiilor plastice, elementele vor fi verificate din punct de
vedere al capacitatii de rotire plastica in conformitate cu Anexa D.4 daca
aceste zone sunt situate intre legaturile intermediare si in conformitate cu
anexa F.3.5 daca zonele sunt situate intre legaturi incastrate la torsiune.
Elementele care nu
formeaza articulatii plastice vor fi verificate in conformitate cu
recomandarile din Sectiunea 5.5 a ENV 1993-1-1 in zonele situate intre
legaturile intermediare aplicate la talpa intinsa si respectiv conform
recomandarilor din Sectiunea 5.5 modificate in cadrul acestei anexe in zonele
situate intre prinderi incastrate pentru torsiune. Acolo unde prevederile
Sectiunii 5.5.4 din ENV 1993-1-1 nu sunt satisfacute datorita prezentei
momentelor si fortelor axiale ce produc solicitari apropiate de rezistenta plastica
a sectiunii, stabilitatea elementului respectiv se va verifica conform Anexei
F.4
In cazul barelor
cu sectiune variabila, respectiv al barelor cu vute nu se accepta aparitia
articulatiilor plastice in zonele variabile si se vor prevedea legaturi laterale
la nivelul coltului interior al cadrului. Daca in aceasta zona apare o
articulatie plastica, rigiditatea elementului de prindere prevazut va satisface
cerintele specifice.
F.3.2 Elemente de baza
Elemente cu
sectiune constanta
In cazul
elementelor cu sectiune constanta, avand sectiunea transversala simetrica in
raport cu axa minima de inertie, sarcina critica elastica pentru compresiune
axiala, Ncr, pentru conditii standard de legatura (vezi mai jos) a
fost determinata de Horne si Ajmani si are expresia:
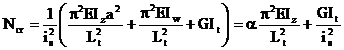
unde:
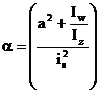
cu urmatoarele
notatii:
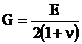
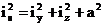
It
= momentul de rasucire libera
Iz
= momentul de inertie minim
Iw
= momentul de rasucire impiedicata care se obtine cu relatia 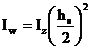
Lt
= este lungimea dintre punctele de legare laterala a ambelor talpi conform Fig.
F1
a
= este distanta dintre axa elementelor de legare laterala (de exemplu axa
centrelor de greutate ale panelor) si centrul de taiere al sectiunii riglei
(vezi Fig. F.2)
h
= este inaltimea sectiunii transversale a riglei
hs
= este distanta dintre centrele de taiere ale talpilor
In cazul
grinzilor cu sectiuni transversale simetrice sau aproximativ simetrice dupa
ambele axe principale de inertie si la care a = 0,75h se lucreaza cu a
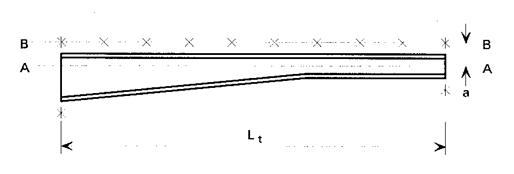
Figura
F.2 - Axa elementelor de legatura si axa elementului verificat
Legenda:
*
= Legaturi ale ambelor talpi din punct de vedere al torsiunii
X
= Legaturi laterale la o singura talpa
A
- A = Axa elementului verificat
B
- B = Axa elementelor de legatura
a
= Distanta dintre axa elementului verificat si axa elementelor de legatura
Lt
= Lungimea pe care se verifica bara
In cazul
elementelor cu sectiune uniforma, avand sectiunea transversala simetrica in raport
cu axa minima de inertie, cu prinderi de tip standard (vezi mai jos), momentul critic elastic Mcr0
pentru pierderea stabilitatii laterale a elementului in cazul unei solicitari
prin moment incovoietor uniform rezulta din formula:
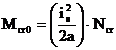
Conditiile
standard de prindere, prezentate in figura F.1 sunt urmatoarele:
(i)
La extremitatile portiunii
verificate de element, avand lungimea Lt
Deplasarea laterala a sectiunii este impiedicata
Rotirea sectiunii in jurul axei longitudinale este blocata
Rotirea sectiunii transversale in plan orizontal este permisa
(ii)
Pe lungimea talpii intinse in zona
verificata:
Deplasarea laterala este blocata
Rotirea sectiunii dupa toate axele este permisa
Legaturile
prevazute la talpa intinsa nu trebuie sa fie continue, cu conditia ca elementul
verificat sa nu isi piarda stabilitatea laterala intre aceste prinderi in
ipoteza ca ar avea legaturi laterale la ambele talpi in punctele respective.
Bare cu sectiunea variabila si bare cu vute
In cazul barelor
avand sectiuni cu talpi de latime si grosime constanta, simetrice dupa axa
minima de inertie, valorile critice Ncr si Mcr0 se
calculeaza conform Sectiunii F.3.2.1 insa cu urmatoarele modificari:
Pentru definirea
distantei "a" dintre axa elementelor de legatura (de exemplu axa centrelor de
greutate ale panelor) si centrul de forfecare al sectiunii grinzii, trebuie
precizata valoarea inaltimii sectiunii transversale a sectiunii variabile la
care se face referinta. Pentru 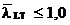 si daca se utilizeaza
coeficientii "c" din Sectiunea F.3.3, se
va lucra cu centrul de forfecare al sectiunii transversale minime conform
figurii F.2. In toate celelalte cazuri se va lucra cu centrul de forfecare al
sectiunii transversale maxime.
si daca se utilizeaza
coeficientii "c" din Sectiunea F.3.3, se
va lucra cu centrul de forfecare al sectiunii transversale minime conform
figurii F.2. In toate celelalte cazuri se va lucra cu centrul de forfecare al
sectiunii transversale maxime.
F.3.3 Formula momentului critic elastic
In cazul
sectiunilor transversale simetrice in raport cu axa minima de inertie si avand
talpi cu sectiune uniforma:
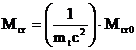
unde Mcr0
este definit in sectiunea F.3.2
In cazul
grinzilor cu sectiune variabila sau cu vute, Mcr0 se calculeaza pe
baza sectiunii transversale minime.
In cazul
grinzilor cu sectiune variabila la care 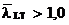 ,daca nu se adopta solutii mai precise, coeficientul "c" se
va lua egal cu 1,0 si se va lucra cu valoarea maxima
,daca nu se adopta solutii mai precise, coeficientul "c" se
va lua egal cu 1,0 si se va lucra cu valoarea maxima 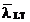 care se obtine de
obicei pentru sectiunea cu inaltime maxima.
care se obtine de
obicei pentru sectiunea cu inaltime maxima.
In cazul barelor
cu talpa interna (a treia talpa care apare de obicei la profilele europene cu
vuta sudata) se va lucra conform Sectiunii F.3.2 utilizand Iw si Iz
calculate cu ignorarea talpii interne iar It calculat cu luarea in
considerare a acestei talpi. Notatiile "mt"si "c" din formula
momentului critic se definesc mai jos.
Factorul momentului
echivalent uniform mt in cazul grinzilor cu inaltime constanta de
sectiune si fara incarcari intermediare intre legaturile de la extremitati
Acest caz nu
apare prea des deoarece cazurile de
incarcare acoperite de ENV 1993-1-1 se refera la incarcari aplicate simultan.
Din acest motiv, in aproape toate cazurile de incarcare, panele acoperisului
sau riglele de perete vor introduce prin reazemele lor forte concentrate
intermediare provenite din greutatea proprie a inchiderilor si din vant. Aceste
forte concentrate sunt incarcari intermediare, asa incat metoda prezentata mai
jos nu este direct aplicabila deoarece presupune o alura liniara (si nu
poligonala) a diagramei de moment
incovoietor intre cele doua extremitati ale elementului. Totusi, daca diagrama
de momente reala poate fi aproximata printr-o diagrama cu alura liniara,
acoperitoare din punct de vedere al stabilitatii laterale a grinzii, acest
moment aproximativ poate fi fi utilizat pentru calculul lui mt
conform prezentei sectiuni.
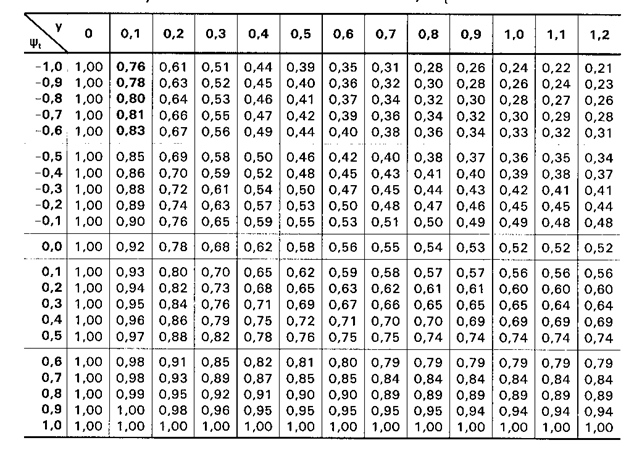
Valorile
momentului echivalent uniform mt rezulta din tabelul F.1
In capul de tabel
se utilizeaza notatia "yt" care reprezinta raportul dintre valoarea minima si valoarea maxima a
momentului. Valorile momentului care comprima talpa nelegata a grinzii se
considera pozitive. Daca valoarea raportului rezulta 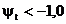 valoarea raportului se
va lua yt=-1,0 conform
celor indicate in Fig. 3
valoarea raportului se
va lua yt=-1,0 conform
celor indicate in Fig. 3
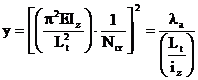
unde:
Ncr
= este incarcarea critica elastica conform Sectiunii F.3.2
la = este zveltetea axiala l definita in Sectiunea F.3.2
Factorul momentului
echivalent uniform mt pentru toate celelalte cazuri
Pentru cazul
general in care momentul incovoietor pe portiunea de bara verificata (cuprinsa
intre punctele de impiedicare a torsiunii) nu prezinta o alura liniara, se
poate aplica urmatoarea formula dedusa de Singh:
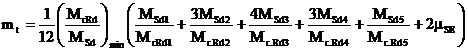
Tabelul F.1 Factorul
momentului uniform mt
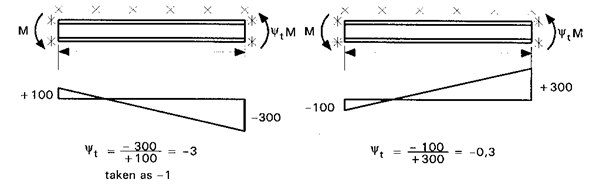
Figura
F.3 Valoarea lui yt
Notatiile MSd1
pana la MSd5 corespund valorile momentelor aplicate la extremitatile
portiunii verificate (unde se afla legaturile pentru torsiune), la sfert, la
jumatate si la trei sferturi de lungime conform Figurii F.4. Se vor lua in
considerare doar valorile pozitive MSd. Valorile lui MSd
sunt pozitive atunci cand produc compresiune in talpa fara legaturi laterale.
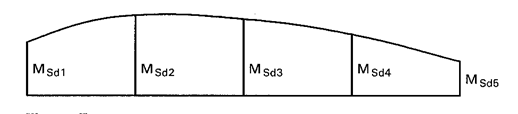
Figura
F.4 Valorile intermediare ale momentului incovoietor
Notatiile Mc.Rd1
pana la Mc.Rd5 corespund rezistentelor la incovoiere ale sectiunii
transversale, in dreptul momentelor aplicate MSd1 pana la MSd5
mentionate mai sus.
Notatia mSE rezulta din relatia:
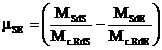
unde:
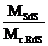 este valoarea maxima
intre
este valoarea maxima
intre 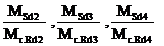
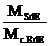 este valoarea maxima
intre
este valoarea maxima
intre 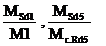
Se vor lua in
considerare numai valorile pozitive mSE
Notatia 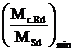
 reprezinta valoarea minima a rapoartelor
reprezinta valoarea minima a rapoartelor 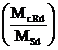 calculate in punctele
1 pana la 5 unde:
calculate in punctele
1 pana la 5 unde:
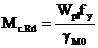 pentru sectiuni
transversale de Clasa 1 sau de Clasa 2 (vezi Sectiunea 5.4.5.2 din ENV 1993-1-1)
pentru sectiuni
transversale de Clasa 1 sau de Clasa 2 (vezi Sectiunea 5.4.5.2 din ENV 1993-1-1)
iar
Wpl reprezinta fie modulul de rezistenta plastic al sectiunilor de
Clasa 1 sau de Clasa 2 in raport cu axa y-y, fie Wef.pl.y pentru
vute ce corespund Anexei E.
Coeficientul "c" al
sectiunii echivalente
In cazul
grinzilor cu sectiune constanta, c=1,0
In cazul
grinzilor cu sectiune I variabila avand 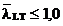 si la care nu apar articulatii plastice pe lungimea
verificata, c=c0,
si la care nu apar articulatii plastice pe lungimea
verificata, c=c0,
Unde c0
rezulta din Tabelul F.2 furnizat mai jos:
Tabelul F.2
Coeficientul sectiunii echivalente "c0"
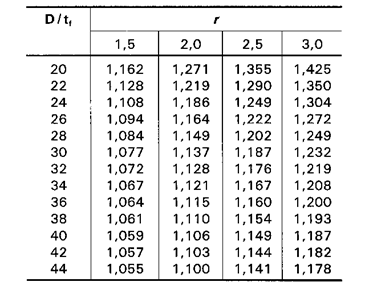
Unde:
r
= este raportul dintre inaltimile sectiunii transversale de la extremitatile
portiunii verificate a grinzii su sectiune variabila sau cu vuta
d1
= este distanta minima intre centrele de greutate ale talpilor externe (vezi
Figura F.2)
d2
= este distanta maxima dintre centrele de greutate ale talpilor externe (vezi
Figura F.2)
D
= este inaltimea minima a sectiunii transversale de la extremitatile portiunii
verificate
tf
= este grosimea medie a talpilor externe
A se observa ca c0
este valabil numai pentru 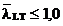 . In cazul cand
. In cazul cand 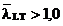 pierderea stabilitatii
laterale poate fi verificata utilizand valoarea maxima
pierderea stabilitatii
laterale poate fi verificata utilizand valoarea maxima 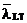 care apare de obicei
la extremitatea barei cu inaltime de sectiune maxima, daca aceasta bara are
latime de talpa constanta si nu prezinta salturi de grosime pentru inima sau
talpi.
care apare de obicei
la extremitatea barei cu inaltime de sectiune maxima, daca aceasta bara are
latime de talpa constanta si nu prezinta salturi de grosime pentru inima sau
talpi.
In cazul
grinzilor cu vuta, de sectiune I, care respecta conditia 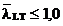 si la care nu apar
articulatii plastice pe portiunea verificata se lucreaza cu coeficientul:
si la care nu apar
articulatii plastice pe portiunea verificata se lucreaza cu coeficientul:
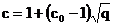
unde: "q" reprezinta
raportul dintre lungimea vutei si lungimea intregului element.
F.3.4 Zveltetea elementelor
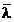 se defineste in cadrul
Sectiunii 5.5.1.2(1) din ENV 1993-1-1 pe baza valorii Ncr dedusa in
conformitate cu paragraful F.3.2
se defineste in cadrul
Sectiunii 5.5.1.2(1) din ENV 1993-1-1 pe baza valorii Ncr dedusa in
conformitate cu paragraful F.3.2
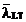 se defineste in
Sectiunea 5.5.2(5) din ENV 1993-1-1 sau
in pragraful F.2.1 in conformitate cu valoarea Mcr conform F.3.3
se defineste in
Sectiunea 5.5.2(5) din ENV 1993-1-1 sau
in pragraful F.2.1 in conformitate cu valoarea Mcr conform F.3.3
De retinut ca
pentru cazurile cu 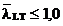 , cand se lucreaza cu factorii "c" din F.3.3, centrul de
forfecare al sectiunii transversale se ia pentru sectiunea cu inaltime minima a
barei, insa in cazurile cu
, cand se lucreaza cu factorii "c" din F.3.3, centrul de
forfecare al sectiunii transversale se ia pentru sectiunea cu inaltime minima a
barei, insa in cazurile cu 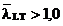 calculele se
raporteaza la sectiunea cu inaltime maxiama barei iar factorul "c" se ia egal
cu 1,0.
calculele se
raporteaza la sectiunea cu inaltime maxiama barei iar factorul "c" se ia egal
cu 1,0.
Zveltetea axiala
a barei l rezulta din formula:
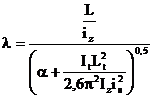
Zveltetea grinzii
lLT rezulta din formula:
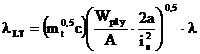
unde "l" este
zveltetea axiala a elementului, definita mai jos in mod acoperitor prin
relatia:
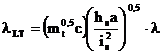
F.3.5 Stabilitatea zonelor invecinate articulatiilor
plastice
Pentru asigurarea
unei capacitati adecvate de rotire a articulatiei plastice, trebuie limitata
zveltetea elementelor de grinda adiacente acesteia in scopul evitarii pierderii
premature a stabilitatii laterale. Aceste elementele cu sectiune variabila,
verificate conform paragrafului F.3, nu vor include alte articulatii plastice
pe lungimea lor aceasta fiind o conditie de aplicabilitate a formulei Horne.
Verificarea se face cu formula:
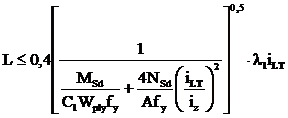
unde "L" este
distanta dintre legaturile pentru torsiune ale sectiunii grinzii (vezi
Sectiunea F.4)
F.4 Deducerea lungimii elementului stabil de grinda
In cele ce
urmeaza se deduce lungimea elementului stabil de grinda, intr-o forma
acoperitoare, corespunzatoare cazurilor in care este prezenta si forta axiala.
Formula de mai jos ia totusi in considerare si interactiunea forta axiala -
moment incovoietor, pentru toate situatiile posibile , conducand la valorile
zveltetilor relative reduse 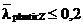 si respectiv
si respectiv 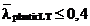 , ceea ce este in concordanta cu prevederile EC.3.
, ceea ce este in concordanta cu prevederile EC.3.
Aceasta formula
adopta o combinatie a eforturilor de tip linear, deoarece formula de
interactiune a compresiunii axiale si a
momentului incovoietor pentru cazurile de zveltete redusa a elementului este
adoptata in forma lineara in cadrul Sectiunii 5.5.4 a ENV 1993-1-1. In acest
mod prezenta procedura de verificare respecta principiile EC.3.
Zveltetile
relative reduse limita din EC.3 sunt:
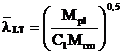
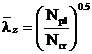
Se calculeaza:
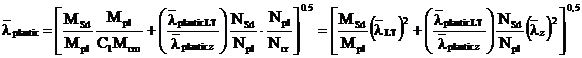
Cand zveltetile
relative reduse sunt egale cu zveltetile limita admise de ENV 1993-1-1, adica :
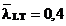 si
si 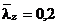 atunci relatia de mai
sus se reduce la:
atunci relatia de mai
sus se reduce la:

Pentru a obtine o
expresie ce necesita mai putine calcule, se scrie:
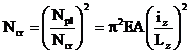
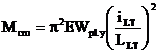


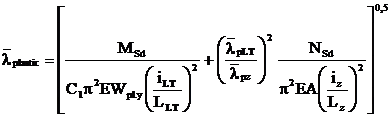
Luand LLT=Lz=L
= distanta dintre punctele de prindere ale grinzii:
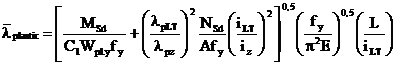
si

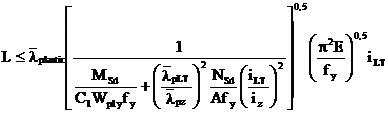
Sectiunea
5.5.2(7) din ENV 1993-1-1 defineste limita de zveltete stabilitate pentru
pierderea de stabilitate laterala prin incovoiere rasucire la valoarea 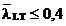 si respectiv pentru
pierderea stabilitatii laterale prin incovoiere la valoarea
si respectiv pentru
pierderea stabilitatii laterale prin incovoiere la valoarea 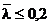
In consecinta,
pentru calculul lungimii stabile a L elementului de grinda, se ia:

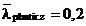
si rezulta:
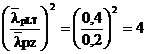
Scriind: 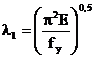
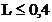
C1
poate fi luat in mod acoperitor ca egal cu 1,0
iLT
pentru cazul sectiunilor laminate la cald poate fi luat egal cu 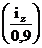


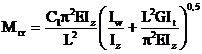
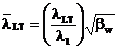
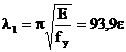
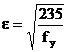 (unde fy
se exprima in N/mm2)
(unde fy
se exprima in N/mm2)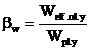 pentru sectiuni eficace de Clasa 2 (conform Anexei E)
pentru sectiuni eficace de Clasa 2 (conform Anexei E)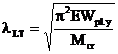
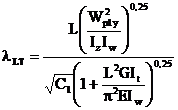
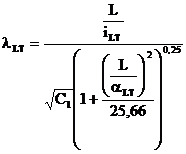
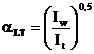
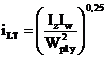
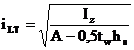
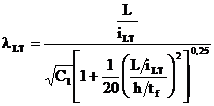
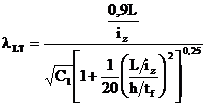
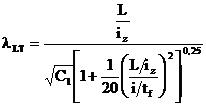

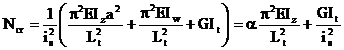
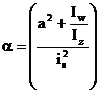
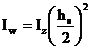

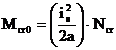
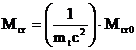
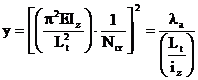
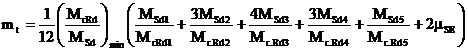



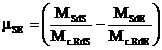
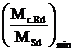
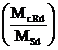 calculate in punctele
1 pana la 5 unde:
calculate in punctele
1 pana la 5 unde: