Importanta
problemelor de optim in automatica
Automatica s-a dezvoltat in principal ca
o tehnica de optimizare, intrucat s-a constatat - inca din perioada initiala a
aplicatiilor automaticii - ca o automatizare care nu este proiectata in mod
corespunzator poate conduce la rezultate mai dezavantajoase decat in absenta
automatizarii respective. Acest lucru poate fi ilustrat in mod simplu prin
faptul ca o bucla de reglare automata care nu respecta conditia de stabilitate
[3, 19] nu poate fi utilizata in practica industriala.
Tendintele de a asigura performante din ce in ce mai bine ale sistemelor
automate - in regimuri stationare si tranzitorii - si de a folosi elementele si
echipamentele de automatizare realizate prin tehnologii curente (deci relativ
ieftine) la capacitatea lor maxima au asigurat un loc central si primordial
problemelor de optimizare in cadrul automaticii si al aplicatiilor acesteia -
automatizarile industriale.
In prezentul subcapitol sunt prezentate
unele tipuri de probleme de optim din domeniul automaticii si automatizarilor
industriale, fiind ilustrata complexitatea actuala a acestor probleme -
datorita uriasei dezvoltari a proceselor tehnologice moderne si cresterii
complexitatii lor - si dificultatile care intervin in rezolvarea unor probleme
de asemenea amploare.
Paragrafele I.2.1 si I.2.2 se refera la
optimizari stationare si optimizari dinamice, doua categorii importante
intalnite in practica industriala, iar paragraful 1.2.3 ilustreaza
descompunerea unor probleme de complexitate ridicata in probleme mai simple in
scopul asigurarii unor conditii mai usoare pentru obtinerea solutiilor.
1.1. Metode
de calcul pentru optimizarea fara restrictii
Problemele de optimizare intalnite in practica sunt probleme
cu restrictii, dar metodele de calcul pentru optimizarea fara
restrictii sunt importante prin faptul ca pot fi folosite cu succes
dupa transformarea problemelor de optimizare cu restrictii in
probleme de optimizare fara restrictii.
1.1.1. Principalele categorii de metode de calcul
Dupa cum se stie, in
cazul functiilor f(x) de o singura variabila, x fiind deci scalar, conditiile
necesare si suficiente de extrem se stabilesc prin intermediul primei
derivate 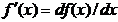 si a celei de a
doua derivate
si a celei de a
doua derivate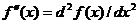 .
.
Conditia necesara pentru un extrem (maxim sau minim) este
anularea primei derivate
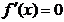 (1.1)
(1.1)
reprezentand conditia
de stationaritate.
Pentru un maxim, conditiile necesare si suficiente sunt 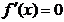 impreuna cu conditia
de concavitate
impreuna cu conditia
de concavitate
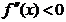 , (1.2)
, (1.2)
iar pentru un
minim conditiile necesare si suficiente sunt 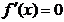 impreuna cu conditia
de convexitate
impreuna cu conditia
de convexitate
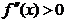 . (1.3)
. (1.3)
Conditia de stationaritate este indeplinita in punctul optim
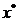 , iar conditia de convexitate este indeplinita in
jurul acestui punct.
, iar conditia de convexitate este indeplinita in
jurul acestui punct.
Conditiile mentionate sunt valabile pentru functii f(x)
cel putin de gradul doi; aceste conditii nu sunt valabile pentru functii
de gradul intai, liniare, de forma f(x) = ax
+ b, intrucat la acestea rezulta
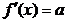 si deci prima
derivata nu depinde de variabila x.
Datorita acestui fapt, metodele de programare neliniara (folosite
pentru optimizarea functiilor criteriu neliniare f(x), unde x este un vector) nu pot fi folosite
pentru rezolvarea problemelor de programare liniara, cu functii
criteriu si restrictii liniare.
si deci prima
derivata nu depinde de variabila x.
Datorita acestui fapt, metodele de programare neliniara (folosite
pentru optimizarea functiilor criteriu neliniare f(x), unde x este un vector) nu pot fi folosite
pentru rezolvarea problemelor de programare liniara, cu functii
criteriu si restrictii liniare.
In cazul optimizarii functiilor criteriu f(x) de variabila
vectoriala, principalele categorii de metode de calcul se disting dupa
faptul ca unele fac apel la primele derivate, altele necesita
derivatele prime si secunde, iar o a treia categorie nu necesita nici
determinarea primelor derivate, nici a derivatelor secunde; cele trei categorii
de metode aproximeaza dezvoltarea in serie Taylor a functiei f(x)
prin retinerea unui numar diferit de termeni.
Metodele din prima categorie pot fi denumite metode de gradient sau metode bazate pe prima variatie,
metodele din a doua categorie pot fi denumite metode Newton sau metode bazate pe a doua variatie, iar
metodele din a treia categorie sunt denumite metode de cautare directa sau metode directe, intrucat
asigura optimizarea apeland numai la valorile functiei criteriu.
Pentru o functie scalara derivabila f(x) de variabila
vectoriala x, 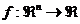 , vectorul gradient (vector linie n-dimensional), care constituie o directie, si are o
importanta esentiala in optimizare, reprezinta prima
derivata si se poate nota prin
, vectorul gradient (vector linie n-dimensional), care constituie o directie, si are o
importanta esentiala in optimizare, reprezinta prima
derivata si se poate nota prin 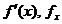 sau prin
sau prin 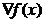 , fiind definit prin derivatele partiale ale functiei,
respectiv:
, fiind definit prin derivatele partiale ale functiei,
respectiv:
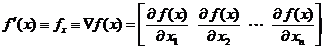 (1.4)
(1.4)
Intr-un punct x1,
gradientul 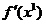 indica directia
in care, pornind din punctul x1,
are loc cea mai abrupta crestere a functiei criteriu f(x).
indica directia
in care, pornind din punctul x1,
are loc cea mai abrupta crestere a functiei criteriu f(x).
De fapt, orice vector n-dimensional
p poate servi ca directie in
spatiul 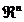 . Astfel, daca se da punctul
. Astfel, daca se da punctul 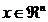 si directia p (cu
si directia p (cu 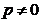 ), atunci punctul
), atunci punctul
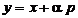 (1.5)
(1.5)
pentru variatii
ale scalarului a intre 0 si 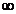 descrie o raza
care porneste din punctul x pe
directia p, iar pentru variatii
ale scalarului a intre
descrie o raza
care porneste din punctul x pe
directia p, iar pentru variatii
ale scalarului a intre 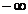 si
si 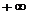 descrie toata
dreapta care trece prin x si
coincide cu directia p.
descrie toata
dreapta care trece prin x si
coincide cu directia p.
Importanta gradientului pentru optimizare rezida si in
faptul ca pentru o anumita directie data p,
produsul scalar
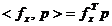 (1.6)
(1.6)
exprima
viteza de variatie a functiei f
de-a lungul directiei p. Astfel,
in analiza matematica se demonstreaza ca pentru o functie f(x)
derivabila in punctul x are loc
relatia [Cal79]
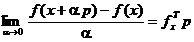 , (1.7)
, (1.7)
expresia (1.7)
fiind denumita derivata Gateaux.
Presupunand ca optimizarea urmareste maximizarea unei functii
criteriu concave f(x), relatia (2.7) permite sa
se demonstreze ca daca f(x) este derivabila in punctul x si exista o directie p pentru care
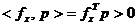 , (1.8)
, (1.8)
atunci exista
t > 0 astfel incat pentru orice valoare 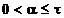 se obtine
se obtine
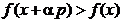 , (1.9)
, (1.9)
deci pe directia
p are loc cresterea functiei
criteriu si apropierea de maxim. Astfel, din (1.7) si (1.8) se obtine
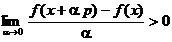 (1.10)
(1.10)
si din definitia
limitei rezulta ca trebuie sa existe t > 0 astfel incat pentru orice 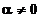 si cuprins intre
si cuprins intre 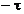 si
si 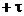 sa se obtina
sa se obtina
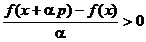 . (1.11)
. (1.11)
Se constata
ca daca se aleg valori a
pozitive care verifica inegalitatea (1.11), relatia (1.9) este
demonstrata. Toate directiile care satisfac conditia (1.8)
asigura cresterea functiei f(x) si deci apropierea de maxim.
Expresiile (1.8) si (1.9) atesta faptul ca gradientul indica
totdeauna spre maxim; in punctul maxim 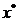 , gradientul este nul, deci:
, gradientul este nul, deci:
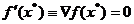 . (1.12)
. (1.12)
Relatia (2.8) arata ca unghiul dintre vectorii fx si p trebuie sa fie mai mic de 90°.
Daca in locul maximizarii unei functii concave, optimizarea
urmareste minimizarea unei functii criteriu convexe f(x),
atunci directiile p trebuie
alese dintre directiile care asigura conditia
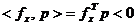 (1.13)
(1.13)
intrucat in acest
caz se va obtine
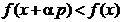 (1.14)
(1.14)
deci pe
directia p are loc
descresterea functiei f(x) si apropierea de minim.
Relatia (1.13) arata ca unghiul dintre vectorii fx si p trebuie sa fie mai mare de 90°,
deci unghiul dintre vectorii -fx
si p trebuie sa fie mai mic
de 90° pentru a se asigura descresterea functiei f(x).
Rezulta astfel ca directia
gradientului fx indica totdeauna spre maximul unei
functii concave, iar
directia -fx indica totdeauna spre minimul unei
functii convexe.
Din considerentele expuse rezulta deosebita importanta a
gradientului pentru desfasurarea procesului iterativ descris de relatiile
de forma (1.54), respectiv
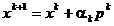 (1.15)
(1.15)
Astfel, presupunand ca iteratia se gaseste in punctul 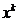 , atunci in cazul
maximizarii unei functii concave directia p a urmatoarei deplasari, spre punctul
, atunci in cazul
maximizarii unei functii concave directia p a urmatoarei deplasari, spre punctul 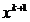 , trebuie
aleasa dintre directiile care satisfac conditia (2.8) in raport
cu gradientul fx,
adica
, trebuie
aleasa dintre directiile care satisfac conditia (2.8) in raport
cu gradientul fx,
adica 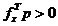 , iar in
cazul minimizarii unei functii convexe directia p a urmatoarei deplasari
trebuie aleasa dintre directiile care satisfac conditia (2.13)
in raport cu gradientul fx,
adica
, iar in
cazul minimizarii unei functii convexe directia p a urmatoarei deplasari
trebuie aleasa dintre directiile care satisfac conditia (2.13)
in raport cu gradientul fx,
adica 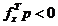
Derivatele secunde intervin in
expresia matricei Hessian, care se obtine
din gradient printr-o noua derivare in raport cu vectorul x. Notand matricea Hessian cu H(x),
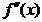 sau fxx, rezulta
sau fxx, rezulta
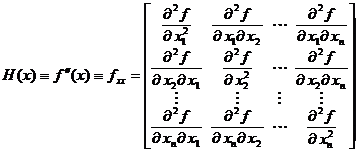 (1.16)
(1.16)
Calculul matricei 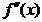 - la fiecare iteratie a
procesului de cautare a optimului - este deosebit de laborios si de
aceea cele mai multe dintre metodele folosite in practica evita acest
calcul.
- la fiecare iteratie a
procesului de cautare a optimului - este deosebit de laborios si de
aceea cele mai multe dintre metodele folosite in practica evita acest
calcul.
In anumite probleme chiar determinarea gradientului poate fi sensibil mai
complicata decat determinarea valorii functiei (uneori gradientul nu
poate fi exprimat analitic); in asemenea cazuri, se prefera metodele de cautare
directa, ilustrate in paragraful 2.5.
1.1.2. Metode de gradient
Ideea metodei gradientului, emisa de A.L. Cauchy in secolul XIX [Cau47] se bazeaza pe o aproximatie de ordinul I, liniara, 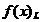 a dezvoltarii in
serie Taylor pentru functia criteriu
a dezvoltarii in
serie Taylor pentru functia criteriu 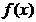 . O asemenea aproximatie pentru dezvoltarea in jurul
unui punct de maxim
. O asemenea aproximatie pentru dezvoltarea in jurul
unui punct de maxim 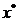 are aspectul
are aspectul
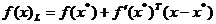 ,
,
unde s-a folosit
notatia 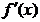 pentru gradient.
pentru gradient.
Dezvoltarea completa in serie Taylor a functiei criteriu 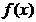 in jurul lui
in jurul lui 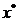 conduce la expresia
conduce la expresia
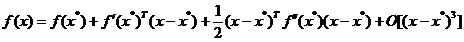 , (1.18)
, (1.18)
unde prin f'(x) s-a notat matricea Hessian din (2.16), iar restul 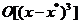 grupeaza toti ceilalti termeni
ai dezvoltarii. Definind diferenta
grupeaza toti ceilalti termeni
ai dezvoltarii. Definind diferenta
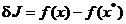 (1.19)
(1.19)
ca variatia
functiei criteriu si notand prin
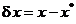 (1.20)
(1.20)
variatia
variabilei vectoriale, din (2.18) se obtine:
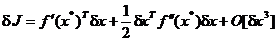 . (1.21)
. (1.21)
Adoptand aproximatia liniara din (2.17), se obtine prima
variatie descrisa prin:
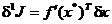 . (1.22)
. (1.22)
In punctele de maxim sau minim prima variatie este nula - avand in
vedere conditia de stationaritate (2.12) - si (2.21) devine
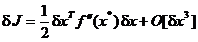 , (1.23)
, (1.23)
termenul
preponderant in aceasta expresie reprezentand-o a doua variatie:
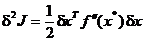 . (1.24)
. (1.24)
Pentru ca punctul 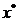 sa asigure un
maxim al functiei criteriu este necesar ca a doua variatie sa
fie negativa - intrucat, conform cu (2.19),
sa asigure un
maxim al functiei criteriu este necesar ca a doua variatie sa
fie negativa - intrucat, conform cu (2.19), 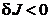 asigura relatia
asigura relatia
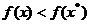 care defineste un
maxim in punctul
care defineste un
maxim in punctul 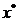 - deci este necesara
conditia:
- deci este necesara
conditia:
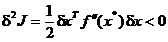 (1.25)
(1.25)
Ca urmare, valorile proprii ale matricei Hessian trebuie sa fie
negative.
In practica se folosesc diferite
variante de metode de gradient. Una din cele mai utilizate este asa numita
metoda a celei mai mari pante
sau a celei mai abrute coborari, in ipoteza
ca optimul cautat este un minim. Aceasta metoda porneste de la ideea
de a adopta in relatia 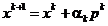 (1.15), o directie p data de
(1.15), o directie p data de
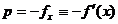 (1.26)
(1.26)
intrucat astfel se
asigura in mod simplu satisfacerea conditiei (1.13) de deplasare spre
minim, deoarece rezulta
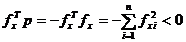 (1.27)
(1.27)
Din (1.15) si (1.26) rezulta ca procesul iterativ de cautare
a minimului este definit de relatia
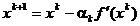 (1.28)
(1.28)
unde 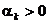
Diversele subvariante ale metodei celei mai mari pante se deosebesc prin
tehnica alegerii valorii pasului 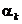 [Cal79]
[Cal79]
Pe langa metoda celei mai mari pante se folosesc si alte variante
de metode de gradient, la unele dintre aceste variante procesul iterativ de cautare
a minimului fiind descris de relatii de forma
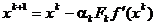 (1.29)
(1.29)
Comparand (1.15) cu (1.29) se constata ca vectorul directiei
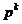 are expresia
are expresia
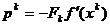 (1.30)
(1.30)
deci, pentru a obtine
din (1.30) relatia (1.26), care defineste metoda celei mai mari pante,
este necesar ca pentru Fk
sa se adopte matricea unitate.
Pentru asigurarea relatiei (1.13), matricea
simetrica Fk -
determinata la fiecare iteratie - trebuie sa satisfaca
anumite conditii.
Compararea diverselor variante de metode de gradient, din punct de vedere
al eficientei, ca si compararea diferitelor categorii de metode de
calcul, reprezinta o problema dificila. In primul rand,
compararea se poate efectua numai pe baza unuia sau mai multor criterii, iar in
practica este necesara considerarea simultana a mai multor
criterii, dintre care unele conduc la rezultate contradictorii.
Criteriile cele mai frecvent utilizate pentru aprecierea unei metode de calcul
se refera la precizia rezultatelor, viteza de convergenta a
procedeului iterativ, timpul de calcul, volumul necesar de memorie a
calculatorului. Primele doua criterii - precizia si viteza de
convergenta - sunt cele mai importante, dar ele nu pot permite o
ordonare univoca a tuturor metodelor de calcul, intrucat estimarea vitezei
de convergenta a unei metode ramane valabila numai pentru o
clasa de probleme, dar nu si pentru altele. De aceea este indicat ca
proiectantul de optimizari sa dispuna de un bagaj cat mai vast
de metode de calcul si de rezultate concrete obtinute in aplicarea
fiecarei metode la anumite clase de probleme.
In cadrul procesului iterativ (1.15), alegerea directiei 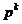 determina viteza
de convergenta, iar alegerea pasului
determina viteza
de convergenta, iar alegerea pasului 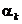 influenteaza puternic volumul de
calcul la fiecare iteratie.
influenteaza puternic volumul de
calcul la fiecare iteratie.
1.1.3. Metode Newton
Metoda gradientului se bazeaza pe aproximarea liniara f(x)L din (1.17)
a dezvoltarii in serie Taylor a functiei criteriu f(x),
deci pe cea mai grosiera aproximatie.
Metoda Newton foloseste o aproximatie patratica f(x)P,
rezultand pentru dezvoltarea in serie in jurul unui punct 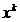 expresia
expresia
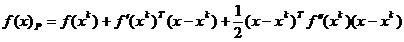 (1.31)
(1.31)
conform cu o relatie
analoaga cu (2.18) (relatia (2.18) a fost scrisa pentru
dezvoltarea in jurul punctului de optim 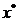 , iar relatia (2.31) - pentru dezvoltarea in jurul
punctului
, iar relatia (2.31) - pentru dezvoltarea in jurul
punctului 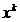 , considerat apropiat de punctul optim
, considerat apropiat de punctul optim 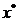 ).
).
Pentru ca punctul de optim 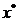 sa asigure
extremul aproximatiei patratice f(x)P este necesara anularea gradientului
acestei expresii pentru x =
sa asigure
extremul aproximatiei patratice f(x)P este necesara anularea gradientului
acestei expresii pentru x = 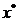 , conditie de tipul (1.12). Calculand gradientul
expresiei (2.31) se obtine
, conditie de tipul (1.12). Calculand gradientul
expresiei (2.31) se obtine
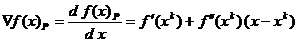 (1.32)
(1.32)
si anuland
valoarea gradientului pentru x = 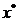 rezulta:
rezulta:
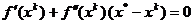 . (1.33)
. (1.33)
Considerand ca matricea Hessian 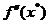 este inversabila,
din (1.33) se obtine:
este inversabila,
din (1.33) se obtine:
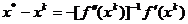 (1.34)
(1.34)
Aceasta relatie atesta faptul ca adoptand in procesul
de iteratie un vector de directie 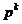 definit de relatia
definit de relatia
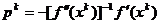 (1.35)
(1.35)
se obtine o
deplasare catre punctul optim 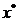 .
.
Astfel, presupunand deocamdata ca in (1.15) se adopta
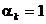 , (1.36)
, (1.36)
relatia (1.15)
devine
 , (1.37)
, (1.37)
iar din (1.34) si
(1.35) rezulta
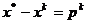 , (1.38)
, (1.38)
inlocuirea
expresiei 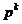 din (1.38) in (1.37)
conducand la relatia
din (1.38) in (1.37)
conducand la relatia
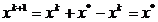 (1.39)
(1.39)
Evident, rezultatul din (1.39) nu este exact, intrucat toate expresiile
anterioare au fost obtinute pe baza aproximatiei patratice f(x)P, dar
el atesta ca deplasarea din xk
pe directia 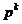 din (1.35) se
efectueaza catre punctul optim
din (1.35) se
efectueaza catre punctul optim 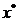 . Inlocuind (1.35) in (1.37) se obtine metoda Newton clasica de calcul:
. Inlocuind (1.35) in (1.37) se obtine metoda Newton clasica de calcul:
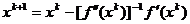 , (1.40)
, (1.40)
corespunzatoare valorii 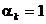 din (1.36).
din (1.36).
Daca extremul este un maxim, directia 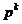 din (1.35) va
satisface conditia (1.8), iar daca extremul este un minim - va satisface, conditia (1.13).
din (1.35) va
satisface conditia (1.8), iar daca extremul este un minim - va satisface, conditia (1.13).
Astfel, facand abstractie de indicele superior k al iteratiei, cu expresia lui p din (1.35) se obtine
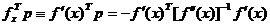 . (1.41)
. (1.41)
In apropierea unui maxim valorile proprii ale matricei Hessian 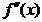 sunt negative - cum a
rezultat din (2.25) - si deci conditia (2.8) este satisfacuta,
iar in cazul unui minim valorile proprii sunt pozitive si ca urmare este
satisfacuta conditia (1.13).
sunt negative - cum a
rezultat din (2.25) - si deci conditia (2.8) este satisfacuta,
iar in cazul unui minim valorile proprii sunt pozitive si ca urmare este
satisfacuta conditia (1.13).
Daca se adopta
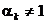 (1.42)
(1.42)
- spre deosebire
de (1.36) - (cu respectarea conditiei a > 0) si se pastreaza directia
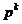 din (1.35), atunci procesul iterativ este descris
de relatia
din (1.35), atunci procesul iterativ este descris
de relatia
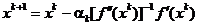 (1.43)
(1.43)
care reprezinta
metoda Newton cu pas variabil (sau metoda Newton generalizata).
Metodele Newton au avantajul ca aproximeaza functia criteriu mult
mai exact decat metodele de gradient, asigura o aproximare mai buna a
solutiilor prin deplasarile pe directia 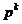 din (1.35) si deci permit obtinerea
unei convergente mai rapide a procesului iterativ decat in cazul metodelor
de gradient.
din (1.35) si deci permit obtinerea
unei convergente mai rapide a procesului iterativ decat in cazul metodelor
de gradient.
In schimb, dupa cum s-a mai mentionat, calculul matricei Hessian -
la fiecare iteratie - este foarte laborios si necesita un mare
numar de operatii aritmetice, ceea ce face ca la metodele Newton numarul
de operatii aritmetice pe iteratie sa fie mult mai ridicat decat
la metodele de gradient, reducandu-se astfel eficienta metodelor Newton. De
aceea au fost cautate metode de calcul care sa convearga aproape
ca metodele Newton, fara a necesita numarul mare de operatii
pe iteratie pe care il implica metodele Newton. Unele dintre metodele
respective, care au in prezent o utilizare din ce in ce mai larga, sunt
mentionate in paragraful urmator.
1.1.4. Metodele directiilor conjugate
Aceste metode folosesc o aproximare patratica a functiei
criteriu fara sa implice calculul explicit al matricei Hessian
la fiecare iteratie, iar informatia necesara aferenta
acestei matrice este obtinuta in decursul catorva iteratii, ceea
ce micsoreaza mult efortul de calcul la fiecare iteratie, fara
ca precizia aproximarii functiei criteriu sa scada
sensibil.
Fiind data o matrice simetrica A 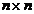 -dimensionala,
directiile reprezentate de vectorii n-dimensionali
p1, p2, , pm
- cu
-dimensionala,
directiile reprezentate de vectorii n-dimensionali
p1, p2, , pm
- cu 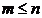 - se numesc A-conjugate daca vectorii
- se numesc A-conjugate daca vectorii 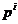 (i = 1, 2, , m) sunt liniar
independenti si daca satisfac relatia
(i = 1, 2, , m) sunt liniar
independenti si daca satisfac relatia
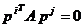 (1.44)
(1.44)
pentru 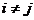 , cu i = 1, 2,, m; j = 1, 2, , m.
, cu i = 1, 2,, m; j = 1, 2, , m.
Sistemul vectorilor p1,
p2, ,
pm este liniar independent
- fiind un sistem ortogonal in metrica definita de matricea A - si ca urmare punctul
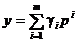 (1.45)
(1.45)
descrie un subspatiu
m-dimensional atunci cand scalarii 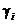 iau valori de la
iau valori de la 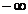 la
la 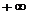 .
.
Pornind de la un punct x1
dat si cu valoarea m data,
cu 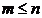 , se
considera punctul
, se
considera punctul
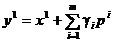 . (1.46)
. (1.46)
Pentru variatii
arbitrare ale scalarilor 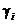 se obtine o varietate liniara m-dimensionala, rezultata din
translarea subspatiului m-dimensional.
se obtine o varietate liniara m-dimensionala, rezultata din
translarea subspatiului m-dimensional.
Daca m = n - si acesta este cazul care
prezinta cel mai mare interes - atunci punctul x1 si cele n
directii A-conjugate genereaza
o varietate n-dimensionala care
coincide cu 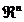 , intrucat vectorii celor n-directii
A-conjugate sunt liniari independenti.
, intrucat vectorii celor n-directii
A-conjugate sunt liniari independenti.
Se poate demonstra [Bri05] ca daca
se adopta o functie criteriu patratica, atunci maximul (sau
minimul) functiei pe varietatea mentionata, care coincide cu 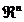 , poate fi determinat numai in n pasi, verificand cate o singura data fiecare din
cele n directii A-conjugate, ordinea verificarii
fiind indiferenta.
, poate fi determinat numai in n pasi, verificand cate o singura data fiecare din
cele n directii A-conjugate, ordinea verificarii
fiind indiferenta.
Construirea directiilor conjugate pentru minimizarea unei functii
patratice a fost propusa de W.C. Davidon [Cal79],
care a elaborat 'algoritmul cu metrica variabila', ideea
fiind dezvoltata de R. Fletcher si M.J.D. Powel [Cal79], rezultand metoda de calcul cunoscuta
sub denumirea 'algoritmul Davidon-Fletcher-Powell' (DFP).
Algoritmul propus de Davidon a introdus o metrica variabila in
relatiile iterative ale metodei celei mai mari pante, in locul expresiei (1.28)
fiind folosita relatia
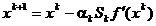 (1.47)
(1.47)
unde matricea Sk, de dimensiune 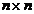 este actualizata la fiecare iteratie
printr-o relatie recursiva. Se constata ca daca in
locul matricei Sk din (1.47)
s-ar introduce matricea unitate, se obtine (1.28). De fapt, in algoritmul
lui Davidon se noteaza
este actualizata la fiecare iteratie
printr-o relatie recursiva. Se constata ca daca in
locul matricei Sk din (1.47)
s-ar introduce matricea unitate, se obtine (1.28). De fapt, in algoritmul
lui Davidon se noteaza
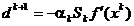 , (1.48)
, (1.48)
iar formula
recursiva pentru obtinerea matricei Sk, care asigura construirea directiilor conjugate, are aspectul
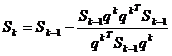 (1.49)
(1.49)
unde 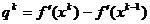 . In
calitate de matrice initiala S0
se alege de regula matricea unitate.
. In
calitate de matrice initiala S0
se alege de regula matricea unitate.
Din (1.43), (1.47), (1.48) si (1.49) se constata ca
algoritmul DFP construieste la fiecare iteratie o aproximatie a
matricei Hessian, bazata pe informatia obtinuta prin intermediul
gradientului. La fiecare iteratie se alege pentru 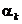 valoarea care
minimizeaza functia
valoarea care
minimizeaza functia
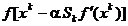 (1
(1
considerata
ca functie de o singura variabila a [Cal79], f(x)
fiind functia criteriu.
Metoda directiilor conjugate poate fi utilizata si la
minimizari de functii criteriu care nu sunt patratice, intrucat
pentru functiile convexe aproximarea patratica este buna, indeosebi
in apropierea punctului de minim.
Rezultatele teoretice ale algoritmului DFP au fost generalizate la o
clasa de algoritmi cu metrica variabila [Cal79].
O varianta interesanta de construire a directiilor conjugate
a fost propusa de Fletcher si Reeves [Cal79],
care au elaborat metoda gradientului conjugat atat pentru minimizarea functiilor
patratice, cat si pentru minimizarea functiilor care nu sunt patratice.
In cadrul acestei variante directiile conjugate sunt generate prin
intermediul relatiei
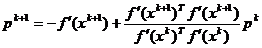 (1.51)
(1.51)
pentru
directia initiala (care porneste din punctul x0) adoptandu-se
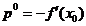
O alta caracteristica a metodei gradientului conjugat consta
in faptul ca gradientii, la diverse iteratii, sunt ortogonali, adica
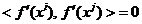 (1.52)
(1.52)
Intrucat la algoritmul DFP apare necesitatea memorarii matricei Sk, 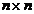 -dimensionala,
pentru problemele de dimensiuni mari, metoda gradientului conjugat apare mai
indicata, necesitand numai memorarea gradientului curent
-dimensionala,
pentru problemele de dimensiuni mari, metoda gradientului conjugat apare mai
indicata, necesitand numai memorarea gradientului curent 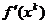 si a directiei curente
si a directiei curente 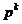 pentru generarea noii
directii
pentru generarea noii
directii 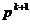 , conform cu (1.51).
, conform cu (1.51).
1.1.5. Metode de cautare directa
Metodele de cautare directa (sau
metodele directe) pot oferi numai solutii aproximative ale problemelor de
optimizare, dar in schimb asigura convergenta pentru orice punct ales
initial, in timp ce metodele care folosesc gradientul, matricea Hessian
sau o aproximatie a acesteia - asemenea metode sunt denumite uneori metode
indirecte - pot oferi solutii exacte, dar necesita un punct
initial bine ales.
In cazul metodelor indirecte, folosirea
indicatiilor date de gradient (sau de gradient si de matricea
Hessian), de exemplu, pentru determinarea unui maxim, poate fi comparata
cu o ascensiune spre un varf de munte care este vizibil in timpul
urcusului, iar folosirea metodelor directe poate fi considerata
analoaga cu o ascensiune in conditii de lipsa de vizibilitate a
varfului (de exemplu pe ceata), cand singurele informatii de
care dispune cel care cauta varful se refera la sesizarea faptului
ca urca sau coboara [Cal79].
Ilustrarea metodelor directe poate fi
facuta mai simplu prin intermediul unei functii de o
singura variabila f(x),
variabila x fiind deci scalara; o asemenea cautare
a extremului este denumita 'de-a lungul unei drepte' (in limba
engleza, 'along a line'), deoarece variabila x ia valori
in 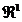 deci
pe o dreapta.
deci
pe o dreapta.
Presupunand ca se cunoaste intervalul de
variatie (a marimii x)
in care se gaseste extremul - de exemplu, se stie ca
intre 0 si 1 exista un maxim, functia f(x) fiind concava -
cautarea directa poate fi efectuata prin mai multe metode.
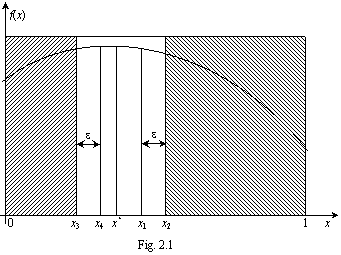 In Fig. 2.1 este ilustrata aplicarea
metodei dichotomiei (injumatatirii intervalului). Metoda prevede
alegerea a doua valori
In Fig. 2.1 este ilustrata aplicarea
metodei dichotomiei (injumatatirii intervalului). Metoda prevede
alegerea a doua valori 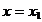 si
si 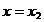 in jurul centrului intervalului, respectiv in jurul valorii x = 0.5,
cele doua valori fiind apropiate intre ele, deci diferind cu o valoare
mica e; se compara valorile
functiei f(x1)
si f(x2)
si daca rezulta, de exemplu
in jurul centrului intervalului, respectiv in jurul valorii x = 0.5,
cele doua valori fiind apropiate intre ele, deci diferind cu o valoare
mica e; se compara valorile
functiei f(x1)
si f(x2)
si daca rezulta, de exemplu
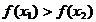
ca in Fig. 2.1, atunci poate fi eliminat intervalul 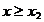 (hasurat in Fig. 2.1), intrucat functia
este concava si maximul se va gasi intre 0 si x2.
(hasurat in Fig. 2.1), intrucat functia
este concava si maximul se va gasi intre 0 si x2.
Se aleg apoi alte doua valori x = x3 si x = x in jurul centrului
intervalului ramas (dintre 0 si x2),
separate tot prin e si se
compara valorile f(x3)
si f(x4)
ale functiei criteriu; daca rezulta, de exemplu
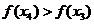
ca in Fig. 2.1, atunci poate fi eliminat si intervalul (hasurat) 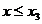 intrucat maximul se va gasi in domeniul x > x3 respectiv in intervalul ramas nehasurat
intrucat maximul se va gasi in domeniul x > x3 respectiv in intervalul ramas nehasurat
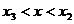
Se continua succesiv cu centrari de
perechi de valori x comparatii
ale valorilor functiei si injumatatirii de interval,
pana la obtinerea unui interval foarte mic in care se
gaseste punctul de optim  deci
pana la obtinerea solutiei aproximative cu o toleranta
admisa.
deci
pana la obtinerea solutiei aproximative cu o toleranta
admisa.
Neglijand valoarea e a
distantei dintre perechile de puncte si avand in vedere ca prin
doua testari ale valorilor functiei criteriu se asigura o
injumatatire a fiecarui interval, rezulta ca
dupa n testari intervalul In,
care ramane de explorat are expresia aproximativa:
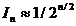 (1.56)
(1.56)
Alte metode de cautare de-a lungul unei
drepte (de exemplu, metoda Fibonacci si metoda sectiunii de aur) au o
eficienta sensibil superioara, reducerea intervalului
initial fiind mai rapida [Ray73].
Metodele de cautare de-a lungul
unei drepte au o importanta deosebita si in cautarea
extremului unei functii criteriu de variabila vectoriala,
intrucat dupa alegerea directiei 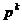 din cadrul procesului iterativ (1.15),
determinarea valorii
din cadrul procesului iterativ (1.15),
determinarea valorii 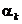 se efectueaza prin gasirea extremului unei functii de variabila
scalara a de-a lungul
directiei
se efectueaza prin gasirea extremului unei functii de variabila
scalara a de-a lungul
directiei 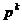 , dupa
cum s-a ilustrat si prin (1.50).
, dupa
cum s-a ilustrat si prin (1.50).
Incercari de a organiza cautarea
directa a punctului de optim, fara determinarea gradientului, au
fost facute si in cazul functiilor criteriu de variabila
vectoriala, fiind elaborate diferite strategii de explorare. In cadrul
celei mai simple strategii fiecare variabila (componenta, a
vectorului x) este succesiv
modificata pana se obtine un extrem - de exemplu, un maxim - al
functiei criteriu pe directia variabilei respective, trecandu-se apoi
la modificarea variabilei urmatoare [Dan76];
procesul este oprit cand nu se mai obtin cresteri ale functiei
criteriu pe directiile niciunei variabile.
O strategie elaborata de Hooke, Jeeve si
Wood [Cal79] prevede executarea dintr-un
punct, a unui 'pas de explorare', reprezentand modificarea
variabilelor cu o mica variatie pozitiva prestabilita;
daca se constata, o apropiere de optimul functiei criteriu, de
exemplu, de un maxim, atunci punctul obtinut devine o 'noua
baza' - spre deosebire de punctul de plecare reprezentand
'vechea baza' - din care se efectueaza noi pasi de
lucru pe directiile tuturor variabilelor (constituind un pas n-dimensional), pe fiecare directie
pasii fiind proportionali cu diferentele valorilor variabilei
respective in noua si vechea baza.
Daca pasul n-dimensional de lucru asigura apropierea de maxim,
urmeaza un nou pas de explorare s.a.m.d. Daca pasul de lucru nu
asigura cresterea functiei criteriu are loc anularea lui si
executarea unui nou pas de explorare.
Daca in directia unei variabile pasul
initial de explorare nu determina o apropiere de maxim, atunci se
efectueaza un pas negativ de explorare pe aceeasi directie; in
cazul cand se obtine o apropiere de maxim, acest pas ramane valabil, dar
daca nici pasul negativ nu marcheaza cresterea functiei
criteriu, atunci pe directia respectiva nu se mai executa nici
un pas de explorare.
O alta strategie, elaborata de Powell [Cal79], foloseste directii conjugate
si converge in n iteratii spre optimul unei functii
criteriu patratice.
Strategia elaborata de Nelder si Mead a
fost numita 'metoda simplex' [Cal79],
intr-un spatiu n-dimensional un
numar de 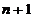 puncte formand un 'simplex'. Pentru
ilustrare, se considera cazul minimizarii unei functii criteriu f(x)
in care variabila vectoriala x
are doua componente, x1
si x ,
deci dependenta
puncte formand un 'simplex'. Pentru
ilustrare, se considera cazul minimizarii unei functii criteriu f(x)
in care variabila vectoriala x
are doua componente, x1
si x ,
deci dependenta 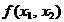 poate fi reprezentata intr-un spatiu
poate fi reprezentata intr-un spatiu 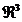 . Intrucat
asemenea reprezentari sunt dificile, se prefera intersectia
corpului care reprezinta dependenta
. Intrucat
asemenea reprezentari sunt dificile, se prefera intersectia
corpului care reprezinta dependenta 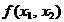 cu o serie de plane paralele cu planul
cu o serie de plane paralele cu planul 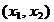 prin
intersectie rezul-tand in fiecare plan cate o curba de valori
constante ale functiei criteriu, numita si 'curba de
nivel'. Proiectand diferitele curbe de nivel in planul variabilelor
prin
intersectie rezul-tand in fiecare plan cate o curba de valori
constante ale functiei criteriu, numita si 'curba de
nivel'. Proiectand diferitele curbe de nivel in planul variabilelor 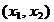 se obtine o imagine de tipul celei din Fig. 2.2, in care punctul M (de
coordonate
se obtine o imagine de tipul celei din Fig. 2.2, in care punctul M (de
coordonate 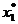
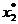 ) corespunde
minimului, deci
) corespunde
minimului, deci
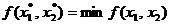 , (1.57)
, (1.57)
iar valorile constante C1,
C2, C3, C4 - ale functiei criteriu pe
diferitele curbe de nivel - sunt din ce in ce mai mici pe masura
apropierii de punctul M deci
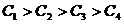
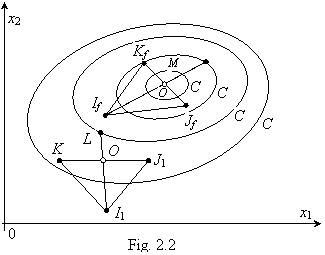 Intrucat in
Intrucat in  un 'simplex' se realizeaza
cu n + 1 puncte, in planul
un 'simplex' se realizeaza
cu n + 1 puncte, in planul  din Fig. 2.2 un
simplex va fi realizat cu 3 puncte, avand forma unui triunghi. Se porneste
de la un simplex initial, de exemplu, I , J1, K1 din Fig. 2.2 si
apoi se cauta inlocuirea punctului (din
simplex) cu cea mai mare valoare a functiei criteriu f(x)
- deci cel mai departat de minim - de exemplu, punctul I cu un alt punct de pe directia
din Fig. 2.2 un
simplex va fi realizat cu 3 puncte, avand forma unui triunghi. Se porneste
de la un simplex initial, de exemplu, I , J1, K1 din Fig. 2.2 si
apoi se cauta inlocuirea punctului (din
simplex) cu cea mai mare valoare a functiei criteriu f(x)
- deci cel mai departat de minim - de exemplu, punctul I cu un alt punct de pe directia  unde O1
se gaseste la jumatatea distantei dintre J1 si K1; in cazul unui numar
mai mare de dimensiuni, punctul O este centroidul tuturor varfurilor ramase
ale simplexului, dupa eliminarea varfului I .
unde O1
se gaseste la jumatatea distantei dintre J1 si K1; in cazul unui numar
mai mare de dimensiuni, punctul O este centroidul tuturor varfurilor ramase
ale simplexului, dupa eliminarea varfului I .
Stabilind, printr-un algoritm adecvat de verificare
a valorilor functiei criteriu, punctul de pe directia 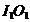 care urmeaza
sa inlocuiasca punctul I1
- de exemplu, punctul L
- se formeaza un nou simplex cu punctele J , K1, L1, continuandu-se operatiile de construire a unei
noi directii pentru inlocuirea punctului cel mai departat de minim
(din cadrul noului simplex) printr-un punct de pe noua directie.
care urmeaza
sa inlocuiasca punctul I1
- de exemplu, punctul L
- se formeaza un nou simplex cu punctele J , K1, L1, continuandu-se operatiile de construire a unei
noi directii pentru inlocuirea punctului cel mai departat de minim
(din cadrul noului simplex) printr-un punct de pe noua directie.
Cand se ajunge in apropierea minimului M, simplexul are aspectul
definit de punctele If,
Jf, Kf, cu directia IfO
pentru inlocuirea punctului If printr-un nou punct; in Fig.
2.2, punctul O coincide cu M ceea ce evident nu este obligatoriu.
Unele metode de cautare directa nu
realizeaza o explorare prin stabilirea unui algoritm de elaborare a
traseului, ca in cazurile mentionate anterior, ci selecteaza in mod
aleator punctele in care se determina valoarea functiei criteriu.
Daca punctele respective acopera complet
gamele de variatie estimate pentru toate variabilele de care depinde functia
criteriu, asemenea metode de cautare directa cu selectare aleatoare a
punctelor de explorare sunt incadrate in clasa metodelor denumite 'Monte
Carlo'. In cadrul
acestor metode, punctul in care a rezultat valoarea extrema a functiei
criteriu este considerat ca optim. De fapt, dupa o prima explorare se
poate stabili daca optimul este localizat intr-o anumita zona
restransa din cadrul celei considerate initial si se poate
calcula probabilitatea apropierii de optim, urmand apoi succesiv noi explorari
aleatoare alternand cu noi reduceri ale zonei.
Elemente de calcul statistic intervin si in
alte aspecte ale rezolvarii problemelor de optimizare, nu numai in
selectarea aleatoare a punctelor explorate. Astfel, in unele cazuri insasi
alegerea directiilor de cautare 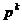 din (1.15) are un
caracter aleator, rezultand metode aleatoare de cautare - prin procedee
iterative - a optimului Cal79 . In alte cazuri, insasi variabilele de care depinde functia
criteriu (sau unii parametri care intervin in aceasta functie) sunt
variabile aleatoare. In asemenea cazuri, optimizarea urmareste gasirea
unui extrem al valorii medii a functiei criteriu, iar metodele de calcul
folosite in acest scop sunt uneori denumite metode de programare stochastica Cal79
din (1.15) are un
caracter aleator, rezultand metode aleatoare de cautare - prin procedee
iterative - a optimului Cal79 . In alte cazuri, insasi variabilele de care depinde functia
criteriu (sau unii parametri care intervin in aceasta functie) sunt
variabile aleatoare. In asemenea cazuri, optimizarea urmareste gasirea
unui extrem al valorii medii a functiei criteriu, iar metodele de calcul
folosite in acest scop sunt uneori denumite metode de programare stochastica Cal79


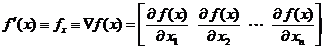 (1.4)
(1.4)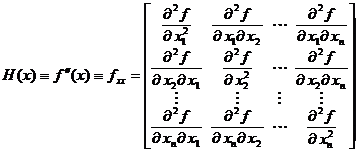 (1.16)
(1.16)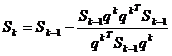 (1.49)
(1.49)
