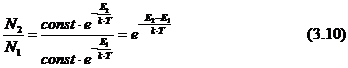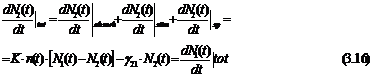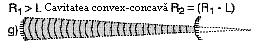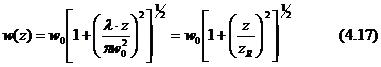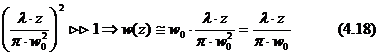Bazele fizicii in laseri

Modelul atomic al lui Bohr, Stari energetice (Nivele), fotoni si diagrame de energie, Absorbtia radiatiilor electromagnetice,Emisia spontana a radiatiilor electromagnetice, Rata de descompunere ,Echilibrul termodinamic (termic), Inversiunea de populatie, Emisia stimulata, Procese posibile intre fotoni si atomi ,Ecuatiile ratei de absorbtie , Diagrama popularii nivelelelor energetice, de absorbtie sau de amplificare, Laserii cu 3 nivele, cu patru nivele, Sistemul laser

Modelul atomic al lui Bohr

Fenomenul laser este un proces care are loc la nivelul materiei. Din moment ce material este compusa din atomi, avem nevoie de a intelege (un pic) structura de atomului, si starile energetice. Vom incepe cu un semi-model clasic, asa cum a sugerat in 1913 Niels Bohr, si l-a numit modelulul atomic al lui Bohr. In conformitate cu acest model, fiecare atom este compus dintr-un nucleu foarte masiv, cu o sarcina pozitiv electrica (Z . e),iar in jurul lui electronii se deplaseaza pe anumite trasee.
  Z este numarul de protoni din nucleu,
  e este sarcina elementara a ectronilor:
  e = 1.6 . 10-19 Coulomb

Figura 3.1 ilustreaza un atom al modelului Bohr:

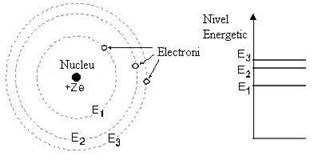
Fig. 3.1 Modelul atomic al lui Bohr

Fiecare 'traseu permis' al electronului in jurul nucleului, este conectat la un anumit nivel de energie.Nivelul de energie este mai mare cu cat distanta de la 'traseu' la nucleu creste. Deoarece pentru fiecare atom exista doar anumite 'trasee permise', numai anumite niveluri discrete de energie exista, si sunt denumite: E1, E2, E3, etc

Stari energetice (Nivele energetice)

Fiecare atom sau molecula din natura are o anumita structura pentru nivelul sau de energie. Cel mai mic nivel de energie este numit nivelul initial, care este nivelul preferat de natura. Atata timp cat atomul nu primeste energie,electronii vor ramane starea initiala. In cazul in care atomul primeste energie (energie electrica, energie optica, sau orice alta forma de energie), aceasta energie este transferata la electroni, si o ridica la un nivel mai mare de energie (in modelul nostrum, mai departe de nucleu). Atomul este apoi considerate a fi intr-o stare instabila (excitat).
Electronii pot ramane doar la anumite nivele de energie membre, care sunt specifice pentru fiecare atom.Electronii nu pot fi intre aceste 'nivele de energie permise', dar pot 'salta' de la un nivel la altul, in timp ce primesc energie, si pot emite cantitati specifice de energie. Aceste cantitati specifice de energie, sunt egale cu diferenta dintre nivelurile de energie in cadrul atomului. Fiecare cantitate de energie se numeste un 'cuantum' de energie.

Transferul de energie catre atom si de la atom

Transferul de energie catre atom si de la atom se poate face in doua moduri diferite:
1.Coliziunile cu alti atomi, si transferul de energie cinetica, ca urmare a coliziunii. Aceasta energie cinetica este transferata catre energia interna a atomului.
    2.Absorptia si emisia de radiatii electromagnetice.
Din moment ce suntem acum interesati de procesul laser, ne vom concentra pe cel de-al doilea mecanism de transfer de energie, catre si de la atom (primul mecanism de excitatie este folosit in anumite lasere, cum ar fi laserul heliu-neon, ca o modalitate de a "pompa" in energie laser).

Fotonii si diagramele energetice

Radiatiile electromagnetice,au in plus fata caracteristica de unda, unele aspecte ale 'comportamentului particulei'. In anumite cazuri,radiatiile electromagnetice se comporta ca un ansamblu de unitati de energie discrete care au impuls. Aceste unitati discrete (cuanta) a radiatiilor electromagnetice sunt denumite 'fotoni'.
Relatia dintre cantitatea de energie (E) a fotonului si frecventa lui (n) este determinata de formula (descoperita prima data de Einstein):

Constanta de proportionalitate in aceasta formula este constanta lui Planck (h): h = 6.626 . 10-34 Joule.sec.
Uneori frecventa unghiulara este folosita in locul frecventei astfel o constanta h este folosita:

Energia este data de:

Aceasta formula arata ca frecventa radiatiei (n) determina energia fiecarui foton in aceasta radiatie. Aceasta formula poate fi exprimata intr-o alta forma forma, prin utilizarea de legaturii intre frecventa (n) si lungimea de unda: c = l·n pentru a obtine:

Aceasta formula arata ca energia fiecarui foton este invers proportionala cu lungime de unda sale. Acest lucru inseamna ca fiecare foton de lungime de unda mai scurta (cum ar fi lumina violet) transporta mai multa energie decat un foton cu lungime de unda mai mare (cum ar fi culoarea rosie). Deoarece h si C sunt constantele universale, deci, fie lungimi de unda sau frecventa este de ajuns pentru a descrie complet fotonul.

Absorbtia radiatiilor electromagnetice

Am vazut ca procesul de fotoni de absorbtie de catre atom este un proces de ridicare a atomului (electroni) de la un nivel mai mic de energie la un nivel mai mare de energie (stare de excitatie), cu o cantitate de energie, care este echivalenta cu energie fotonului absorbit. Discutia noastra a implicat un sistem microscopic in care un foton interactioneaza cu un atom.
Intr-un sistem macroscopic,atunci cand radiatiile electromagnetice trec prin materie, o parte din ea este transmisa, si o parte abosorbita de atomi.
Intensitatea (I) a radiatiilor tansmise printr-un material omogen de grosime (x) din, este descris de catre ecuatia experimentala a absorbtiei exponentiale (Legea lui Lambert):

I₀ =intensitatea radiatiei incidente

a=coeficientul de absorbtie al materialului

Cu cat este mai gros materialul, cu atat este mai mica intensitate fasciculului transmis. Relatia dintre intensitatea transmisa(I) intensitatea incindenta (I₀) descrie transmisia (T) din acest material:

Din ultimele doua ecuatii obtinem tansmisia:

Este normal sa se foloseasca centimetrul ca unitate de masura pentru grosimea materialului astfel incat unitatea de masura pentru coeficientu de absorbtie (a) este cm^-1

Fiecare material reactioneaza diferit,in functie de lungimea de unda,astfel coeficientul de absorbtie este o functie de lungimea de unda: α (l) .Acest fapt este foarte important (dupa cum vom vedea) pentru a intelege interactiunea radiatiilor electromagnetice cu materia, in varietate de aplicatii laser.
  Pentru o anumita grosime (x) a materialului absorbtia depinde numai de coeficientul de absorbtie caracteristic fiecarui material.
  
Emisia spontana a radiatiilor electromagnetice

Unul dintre principiile de baza in fizica (care sta la baza unui subiect in termodinamicia) este ca:
Fiecare sistem din natura 'prefera' sa fie in cele mai mic nivel energetic.Acest nivel este numit nivelul initial. Ca un exemplu, am mentionat acest principiu in modelul atomic al lu Bohr. Atunci cand energia este aplicata unui sistem, atomii din material sunt excitati, si ridicati la un nivel mai mare de energie. (termenii 'atomi excitati', "stari excitate", precum si "electroni excitati" sunt folosite aici cu nici o distinctie) .
Acesti electroni vor ramane in starea de excitatie pentru o anumita perioada de timp, si apoi vor reveni la stari energetice mai mici si vor emite energie, de valoare exacta a diferentei dintre nivelurile energetice DE). In cazul in care acest pachet de energie este transmisa ca energie electromagnetica, aceasta se numeste foton.
Emisia fotonului individual este aleatoare, fiind efectuata individual de catre fiecare atom de excitat, cu nici o legatura cu fotonii emisi de alti atomi. Cand fotonii sunt emisi in mod aleatoriu de atomi diferiti in momente diferite,procesul se numeste emisie spontana. Deoarece aceasta emisie este independenta de influenta externa, nu exista nici o directie preferata de catre fotoni, si nu exista nici o legatura de faza intre fotonii emisi de diferiti atomi.


Rata de descompunere

Pierderea de energie de catre un atom excitat se poate face in doua moduri:

-descompunerea fara emisie de radiatie - prin transferul de energie la vibratiile mecanice ale atomilor vecini. Rata pentru acest tip de descompunere este g_nr.Efectul macroscopic al acestor vibratii este ceea ce noi numim de caldura (sau o crestere semnificativa a temperaturii).
-descompunerea prin emisie de radiatie - prin emisie spontana la o rata de g_rad .
Cateva exemple de descompunere prin emisie de radiatie:
   Intr-un material fosforescent,atomii sunt excitati de radiatii la o lungime de unda, si dupa ce se opreste excitatie, putem vedea inca (cu o iluminare corespunzatoare) o vapaie, care este generata de fotonii emisi de atomii excitati atunci cand revin la starea lor de echilibru.
  Atomii de neon in interiorul unui tub sunt excitati de o descarcare electrica. Cand acesti atomi revin la starea lor de echilibru, ei emit fotoni in spectrul vizibil. Neon-ul este transparent la radiatii in spectrul vizibil, dar spectrul emis dintr-un neon este in zona portocaliu-rosu a spectrului. Zona naturala de absorbtie a spectrului de atomi de neon este in ultra-violete (UV) , dar intr-un tub de neon,gazul este ionizat, din cauza descarcarilor electrice.Atomii ionizati ai neonului emit radiatii vizibile.
Valoarea totala a ratei de descompunere a unui anumit nivel este suma a ratelor de descompunere a doua procese:

Ordinele de magnitudine pentru timpul de descompunere pentru atomi:
  Descompunere fara emisie de radiatie: picoseconds - microsecunde (10.12 - 10.6 sec) - foarte repede.
  Descompunere cu emisie de radiatie: microsecunde - milisecunde (10.6 - 10.3 sec)


Echilibrul Termodinamic(Termic)

De la termodinamica stim ca o colectie de atomi, la o temperatura T [0 K], in echilibru termodinamic cu ce il inconjoara, este distribuit astfel incat la fiecare nivel de energie este in medie un anumit numar de atomi. Numarul de atomi (Ni) la nivelul specific de energie (Ei) se numeste numarul populatiei.
Ecuatia Boltzmann determina raportul dintre numarul populatiei de pe un anumit nivel de energie si temperatura:

Ni = Numarul populatiei, numarul de atomi pe unitatea de volum la un anumit nivel energetic, Ei.
k = constanta Boltzmann: k = 1.38 . 1023 Joule / 0K.
Ei = energie de nivel I. Presupunem ca Ei> Ei-1.
Const = constanta de proportionalitate. Nu este importanta, atunci cand vom considera un nivel de populatie, comparativ cu populatia de un alt nivel, asa cum vom vedea in curand.
T = Temperatura in grade Kelvin, 0 K (temperatura absoluta).
Ecuatia Boltzmann arata dependenta numarului populatiei (Ni) cu privire la nivelul de energie (Ei), la o temperatura T.
Din aceasta ecuatie vom vedea ca:
  1. Cu cat este mai mare temperatura, cu atat este mai mare numarul de populatie.
  2. Cu cat este mai mare nivelul de energie, cu atat este mai mic numarul de populatiei.
  Populatia relativa din doua niveluri de energie E2, comparativ cu E1 este:

 

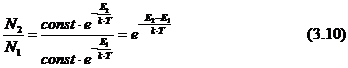
Concluzii:
1.Raportul intre doua numere de populatie (N2 / N1) nu depinde de valorile nivelurilor de energie E1 si E2,ci numai de diferenta dintre ele: E2 - E1.

2.Pentru anumite diferente de energie, cu atat este mai mare de temperatura, creste populatia relativa.
3.Populatia relativa poate fi intre 0 si 1.

Populatia la echilibru termodinamic

Figura 3.2 arata populatiei din fiecare nivel de energie la termodinamice de echilibru.

 

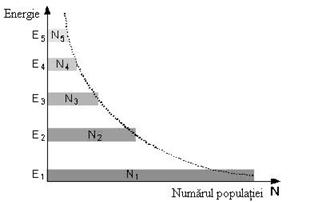Figure 3.2: Numarul populatiei in cadrul unei "populatii normale"

Figura 3.2 ilustreaza valorile nivelului de energie pe axa y, corespunzatoare populatiei pe axa x. Daca am interschimba axele, vom obtine o histograma in care inaltimea fiecarei coloane afiseaza numarul populatiei din fiecare nivel. Latimea nivelurilor de energie in aceasta figura este arbitrara, si nu corespunde cu cea reala a fiecarui nivel.
In ecuatie, cel de-al doilea termen din paranteza este intotdeauna mai putin de 1. Deci, paranteza este intotdeauna mai mica decat 1. Astfel, cele mai importante concluzii ar fi:
1.In echilibrul termodinamic , numarul de populatie al nivelurilor de energie mari este intotdeauna mai mic decat numarul populatiei a unui nivel mai mic de energie.

2.Cu cat este mai mica diferenta dintre nivelurile de energie, cu atat mai mica este diferenta intre populatia dintre aceste doua niveluri.
Fizic, electronii din interiorul atomului prefera sa fie la cel mai mic nivel posibil de energie. Chiar si atunci cand acestia sunt excitati la un nivel mai ridicat, se intorc inapoi la cel mai scazut nivel de energie, dupa o perioada scurta de timp.

Inversiunea de populatie

Am vazut ca intr-o ecuatie termodinamica de echilibru Boltzman ne arata ca:
N1> N2> N3
Astfel, numarul de populatie dintr-un nivel energetic mare sunt mai mici decat numarul populatiei din nivelele mai mici. Aceasta situatie se numeste 'populatie normala'. Intr-o situatie normala de populatie un foton ajuns pe material va fi absorbit, si un atom se ridica la un nivel superior. Prin pomparea energiei intr-un sistem de atomi, putem realiza o situatie de 'inversare a populatiei'. In inversarea populatiei, cel putin unul dintre cele mai mari niveluri de energie are mai multi atomi decat un nivel mai mic de energie.
Un exemplu este descrisa in Figura 3.3b. In aceasta situatie, exista mai multi atomi (N3), intr-un nivel ridicat de energie (E3), decat numarul de atomi (N2),aflat intr-un nivel mai redus de energie (E2).

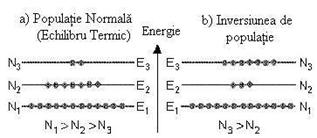
Figure 3.3: 'populatia normala' comparata cu 'inversiunea populatiei"

Emisia stimulata

Atomii stau intr-un nivel excitat numai pentru o perioada scurta de timp (in jur de 10^-8 sec), apoi se intorc la un nivel mai redus de energie prin emisie spontana .Fiecare nivel de energie are o medie de viata caracteristica, care este perioada de timp in care numai 1 / e (circa 37%) din atomii excitati raman in aceasta stare. Astfel, acesta este momentul in care 67% din atomii excitati au revenit la un nivel mai mic de energie.
In conformitate cu teoria cuantelor, trecerea de la un nivel de energie la altul este descris de probabilitatea statistica. Probabilitatea de tranzitie de la un nivel de energie mai mare catre unul mai mic este invers proportionala cu durata de viata a celui mai ridicat nivel de energie. In realitate, probabilitatea diferitelor tranzitii este o caracteristica a fiecarei tranzitie, in conformitate cu regulile de selectie.
In cazul in care probabilitatea de tranzitie este mica pentru o anumita tranzitie, durata de viata al acestui nivel de energie este mai mare (de aproximativ 10^-3 sec), iar acest nivel devine 'meta-stabil'. In acest meta-stabil o mare populatie de atomi se poate forma. Asa cum vom vedea acest nivel poate fi un candidat pentru procesul laser.
In cazul in care numarul populatiei a unui nivel mai mare de energie este mai mare decat numarul populatiei a unui nivel mai scazut de energie, o conditie de 'inversiune de populatie' este stabilita. Daca exista o inversare de populatie intre doua niveluri de energie, probabilitatea este mare, ca un foton sa stimuleze un atom excitat sa revina la o stare energetica mai mica, in timp ce emite un alt foton de lumina. Probabilitatea pentru acest proces depinde de corespondenta intre energia fotonului incident si de diferenta dintre cele doua niveluri.

Proprietatile radiatiei laser

Fotonul care este emis in procesul de emisie stimulata este identic cu fotonul incident. Ambele au:
1.lungimi de unda identice(si, astfel, frecvente) - monocromaticitatea.
2.directii identice in spatiu - directionality.
    3. faze indentice - coerenta.
Acestea sunt proprietatile de radiatie laser.
Fotonul incident nu se schimba deloc, ca urmare a procesului de emisie stimulata. Ca urmare a procesului de emisie stimulata, avem doi fotoni identici cu un foton si o stare de excitatie. Astfel avem amplificare, in sensul ca numarul de fotoni a crescut.

Procese posibile intre fotoni si atomi

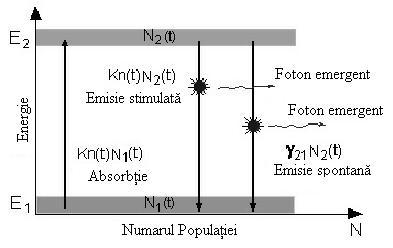
Figura 3.4 rezuma trei posibile procese intre fotoni si atomi: absorbtia, emisie spontana, precum si emisia stimulata.

Absorbtia de fotoni: Un foton cu frecventa n₁₂ loveste un atom in starea initiala, si il impinge la nivel mai mare de energie (E2), in timp ce fotonul este absorbit.

Emisia spontana a fotonilor:Un atom intr-o stare excitata (stanga) emite un foton cu frecventa n₁₂ si se indreapta catre un nivel energetic scazut.

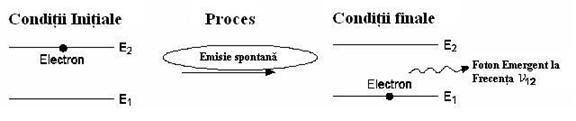
Ecuatiile emisiei spontane

Pentru simplitate vom presupune:
  1. Materialul este compus din mai multi atomi identici.
  2. Fiecare atom are doar doua nivele de energie: E1 si E2.
  3. Singurul mecanism de degradare al nivelului de energie E2 este de emisia spontana.
  4. La momentul t, un numar N1 de atomi sunt in nivelul de energie E1, si N2 atomi de energie la nivel E2.
Rata la care populatia excitata N2 (t) coboara de la nivelul mai mare de energie (E2), la nivel mai redus de energie (E1),prin emisie spontana este dat de coeficientul de g₂₁ , inmultita cu numarul de populatie instantanee al acestui nivel N2(t), astfel cum au fost descrise de primul ordin al ecuatiei diferentiale:

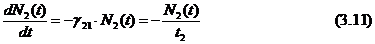
Aceasta ecuatie defineste durata de viata t₂ al nivelului de energie E₂:

Solutia ecuatiei diferentiale este:

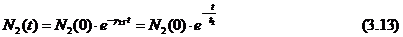
Tranzitii stimulate (fortate)

Puterea unui semnal optic (numarul de fotoni) este descrisa de intensitatea (I), ceea ce inseamna raportul dintre puterea masurata pe o anumita suprafata (cum puterea este o masura a cantitatii de energie in timp,iar intensitatea este o masura a cantitatii de energie in timp pe o suprafata).
Densitatea de energie n (t) - numarul de fotoni pe unitatea de volum, energia radiatiilor electromagnetice in unitati de hn sau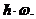
Un semnal optic este un camp electromagnetic oscilant, si un atom poate fi descris ca un dipol electric.
Cand un semnal optic de frecventa corespunzatoare (hn egal cu diferenta de energie dintre nivelurile energetice E2 - E1) se apropie de un atom, ambii atomi la nivel mai redus de energie (E1) cat si cel de la un nivel superior de energie (E2) va incepe sa oscileze.
De aceea, exista doua procese fortate: absorbtia si emisia stimulata.


Ecuatiile ratei de absorbtie

Semnalul optic incident (fotonii) determina atomii la un 'salt' de la un nivel mai redus de energie (E1), la nivel superior de energie (E2).
Rata de absorbtie este proportionala cu produsul dintre densitatea n (t) a fotonilor incidenti (numarul de fotoni intr-o unitate de volum), cu numarul de atomi N1 (t),a nivelului mai scazut de energie (E1):

Fiecare foton excita un atom catre cel mai ridicat nivel de energie.
K - constanta de proportionalitate, este o masura relativa a fortei de raspuns a atomului la radiatiile incidente in aceasta tranzitie.



Ecuatiile emisiei stimulate

Semnalele optice incidente (fotonii) determina atomii de la un nivel superior de energie (E2) sa oscileze (oscilatii fortate), si sa faca o tranzitie la nivel mai redus de energie (E1).
In acest proces doi fotoni sunt emisi impreuna: fotoniul incident si fotonul provenit din energia de tranzitie hn = E2 - E1.
Rata emisiei stimulate este proportionala cu produsul dintre densitate de energie n (t) a fotonilor incidenti (numarul de fotoni intr-o unitate de volum), cu numarul de atomi (N2 (t)) a nivelului superior de energie (E2) :

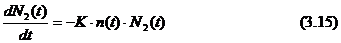
Constanta de proportionalitate (K)

Din consideratiile cuantice deducem constanta de proportionalitate (K), pentru emisie stimulata si pentru absorbtia stimulata ca fiind identica. Aceasta constanta depinde de frecventa (n) a fotonului incident. Valoarea lui K este maxima atunci cand frecventa fotonului incident este egala cu frecventa de tranzitie n₂₁
Cu cat este mai departe de frecventa de tranzitie, cu atat este mai mica valoarea constantei de proportionalitate, pana la zero. Fiecare tranzitie are o banda Dn in jurul frecventei de tranzitie. Aceasta banda arata domeniul de frecventa in care pot sa apara tranzitii. Daca frecventa fotonului de incindeta nu este in intervalul n₂₁+Dn , atunci valoarea lui K este zero.

Diagrama de energie a nivelului de populatie

Vom rezuma toate tranzitiile in diagrama de energie a nivelulului de populatiei (figura 3.5).

	Figure 3.5 Diagrama de energie a nivelului de populatie

Ecuatia pentru populatia de nivel E2 rezuma emisia spontana si doua emisii stimulate, pentru cazul simplu al unui sistem de nivelul doi:

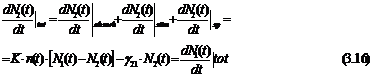
Figure 3.5: Schematic energy level diagram

Ar trebui sa ne amintim ca emisia spontana si emisia stimulata de apar in acelasi timp, si sunt independente una de cealalta, astfel incat ratele lor de emisie poate fi adunate.
Procesul de emisie stimulata este un rezultat al raspunsului in rezonanta al atomului la semnalul de forta, astfel incat acestia vibreaza la aceeasi frecventa si sunt coerente in spatiu si timp (cu aceeasi faza si amplitudine). Pe de alta parte,emisia spontana este in toate directiile in spatiu, si fiecare foton este emis in mod aleatoriu.


Amplificarea

Am vazut in ecuatie ca doua procese scad numarul populatiei al unui nivel excitat: emisia spontana si emisia stimulata.
  Un singur proces creste numarul populatiei unui nivel superior - procesul de absorbtie.Cum aceeasi cantitate de energie (hn) este implicata in fiecare tranzitie in sus sau in jos, decat rata la care energia este absorbita intr-o unitate de volum de atomi este data de rata de tranzitie de ori unitatea de energie:

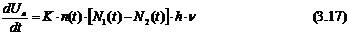
U_a este densitatea de energie in tranzitiile stimulate.Aceeasi ecuatie poate fi scrisa pentru densitatea de fotoni:

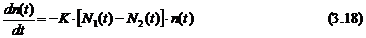
Energia incindenta este:

Energia absornita este luata din semnalul incident,asa ca pierderile din semnalul incident sunt:

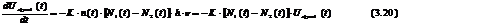
Absorbtie sau amplificare
 
Din ecuatia ratei pierderilor de energie a semnalului de intrare, vom vedea ca semnul diferentei in numarul populatiei DN = N1 (t) - N2 (t) determina daca densitatea de energie a semnalului de intrare va creste sau va scadea, in functie de timp.
Consideram doua situatii:
    1.Cand o colectie de atomi este intr-o populatie normala (echilibru termic), numarul de populatie al nivelului de energie mai mic (E1) este mai mare decat numarul populatiei din nivelul de energie mai mare (E2): N1 (t)> N2 ( t).
  In aceasta situatie, este posibila doar absorbtia, si ca un rezultat atomii vor primi energie de la semnalul de intrare, care va scadea in marime.
    2.Cand o colectie de atomi se afla intr-o inversiune de populatie, semnul in fata parantezei este minus, iar semnalul va creste, inseamna amplificare. Energie de la sistemul de atomi va fi transferat semnalului de intrare, si o amplifica la intr-un ritm care este proportional cu diferenta dintre numerele de populatie si cu intensitatea semnalului de intrare.

Concluzie:

In cazul in care un material este in echilibru termic, doar absorbtia poate aparea, si nici o amplificare.
Pentru a produce amplificare, materialul trebuie sa fie intr-o inversare a populatiei, in care mai multe atomi sunt pompati la o stare de excitatie, comparativ cu un nivel mai mic energetic.
Dupa intelegerea procesului de amplificare, la nivel microscopic al atomului,vom conecta acest process la un sistem macroscopic, asa cum am facut in procesul de absorbtie a radiatiilor electromagnetice.
In procesul de absorbtie in mediu laser, coeficientul de absorbtie (a) depinde de material, precum si cu privire la diferenta de populatie (D N = N₁(t)-N₂(t)) intre nivelele de energie E1 si E2,este:

a = K(N₁- N₂)

Constanta de proportionalitatea (K), depinde de material si de lungimea de unda a radiatiilor laser. Atata timp cat N1 (t)> N2 (t), a este pozitiv, iar procesul este de absorbtie. In situatia ' inversiunii de populatie ', N1 (t) - N2 (t) <0, astfel incat N2 (t)> N1 (t).
Conform legii Lambert: I = I₀e^-AX, factorul (-ax) este pozitiv ceea ce inseamna ca intensitatea la iesire (I) este mai mare decat intensitatea la intrare (I₀), astfel rezulta amplificarea (castig de energie ).
In cazul amplificarii, a se numeste coeficient de crestere.
Probabilitatea tranzitiei stimulate de catre radiatia incidenta este identica pentru cele doua procese (de absorbtie si de emisie stimulata).Directia in care se vor produce mai multe procese depinde de populatia din nivelul energetic in acel moment.

Concluzie:

Cu cat lungimea mediului activ este mai mare, creste amplificare.
Nu exista o limita la aceasta concluzie. In discutia de mai sus de absorbtia in mediul activ nu a fost luata in considerare.

Laserul cu 3 niveluri de energie

O diagrama schematica a nivelului de energie a unui laser cu trei nivele de energie este prezentata in figura 3.6. Cele doua nivele de energie intre care apare fenomenul laser sunt nivelul (E1) de energie mai mica, si nivelul (E2) de energie superioara.

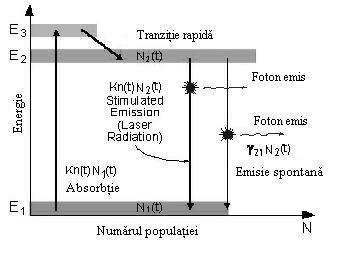
Figure 3.6: Diagrama nivelelor energetice intr-un laser cu trei nivele

Pentru a simplifica explicatia, vom neglija emisia spontana. Pentru a realiza fenomenul laser, energia trebuie sa fie pompata in sistem pentru a crea inversiunea populatiei. Asa ca mai multi atomi vor fi in nivelul de energie in E2 decat la nivelul (E1). Atomii sunt pompati de la nivelul de baza (E1) la nivelul de energie E3. Ei stau acolo pentru un timp mediu de 10^-8 sec, si dezexcitarea (de obicei cu o tranzitie fara emisie de radiatie) ii conduce la nivelul meta-stabil E2. Avand in vedere ca durata de viata a nivelul de energie meta-stabil (E2) este relativ lung (de ordinul a 10^-3 sec), multi atomi raman la acest nivel. Daca pomparea este suficient de puternica, la finalul ei, mai mult de 50% din atomi vor fi la nivelul de energie E2, o inversiune de populatie exista, si fenomenul laser poate sa apara.

Laserul cu patru nivele de energie

O diagrama schematica a nivelului de energie a unui laser cu patru nivele de energie este prezentata in figura 3.7. In comparatie cu diagrama unui laser cu trei nivele, exista un plus de energie la nivel deasupra nivelului de baza. Acest nivel de energie in plus are o durata de viata foarte scurta.

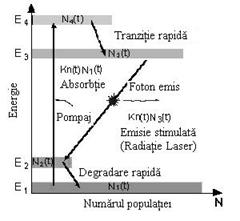
Figura 3.7. Diagrama nivelurilor energetice intr-un laser cu patru nivele

Operatiunea de pompare a unui laser cu patru nivele este similara cu pomparea unui laser cu trei nivele. O rapida populare a nivelului (E3) este posibila prin intermediul nivelului superior de energie (E4). Avantajul oferit de laserul cu patru nivele este populatia scazuta de la nivelele mai mici de energie (E2). Pentru a crea inversarea populatiei, nu este necesar pentru a pompa mai mult de 50% din atomi catre nivelul superior. Populatia nivelului inferior (N2 (t)) se dezexcita rapid si se indreapta spre nivelul 1, deci, practic, acesta este gol. Astfel, o functionare completa a laserului cu patru nivele este posibila, chiar daca 99% din atomi raman in cadrul nivelului incipient.
Avantajele laserului cu patru nivele comparativ cu laserul cu trei nivele:
Pragul de declansare a fenomenului laser este mai mic in cadrul laserului cu patru nivele.
  Eficienta este mai mare.
  Rata de pompare este mai mica.
  Functionarea continua este posibila.


Sistemul Laser

Laserul este un sistem care este similar cu un oscilator electronic.Un oscilator este un sistem care produce oscilatii fara un mecanism extern de conducere. Pentru a demonstra un oscilator, putem folosi analogia cu sistemele acustice:

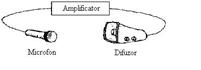
	Figure 3.8 Analogia cu un sistem audio

Un sistem de amplificare a sunetului are un microfon, un amplificator si difuzor. Cand microfonul este plasat in fata difuzorului, un circuit inchis este format, si un fluierat este emis de difuzor.Fluieratul este creat spontan, fara nici o sursa externa.
Explicatie: Zgomotul de fond al difuzorului este detectat de microfon, amplificat si semnalul amplificat este din nou colectat de microfon. Acest feedback pozitiv continua pana la un fluierat foarte puternic.
Fiecare Oscilator are 4 parti principale (asa cum se vede in figura 3.8):
  1. Amplificator.
  2. Feedback-ul pozitiv de rezonanta.
  3. Cuplajul de iesire.
  4. Sursa de energie.

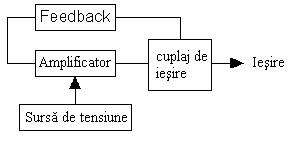
	Figura 3.9: Oscilatorul electronic

In analogie cu amplificatorul electronic, laserul poate fi descris ca fiind compus din patru unitati structurale (vezi figura 3.10):
  1.Mediul activ, care serveste ca un amplificator optic.
  2. Mecanismul de excitatie.
  3. Feedback-ul optic.

4.Cuplajul de iesire,pentru a permite radiatiei electromagnetice sa iasa din dispozitivul laser.

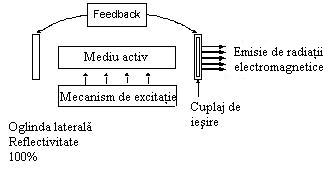
Figura 3.10 Principiul de baza al laserului

Mediul activ laser

 Mediul activ este o colectie de atomi si molecule, care pot fi excitate intr-o inversiune de populatie, si pot fi extrase radiatii electromagnetice din aceasta emisie stimulata. Mediul activ poate fi in orice stare a materiei: solide, lichide, gaze sau plasma.Mediul determina lungimile de unda, care pot fi emise de laser. Aceste lungimi de unda sunt determinate de anumite tranzitii intre nivelele de energie in acest material. Lista de materiale care determina aparitia fenomenului laser, in anumite conditii de laborator include sute de substante, iar numarul lor creste in timp.Principiul laserului este similar pentru toate tipurile de laser, si noi vom folosi termenul de 'mediu activ' si vom presupune ca este compus din 'atomi'. In realitate,mediul activ poate fi atomi, molecule, ioni, sau semiconductori, in functie de tipul de laser.

Mecanismul de excitatie

Mecanismul de excitatie este sursa de energie care ridica atomii in mediul activ in starea de excitatie, creand astfel inversiunea de populatie. In conformitate cu legea de conservare a energiei, aportul de radiatii electromagnetice care parasec laserul este intotdeauna mai mic decat aportul de energie din mecanismul de excitatie. Exista lasere cu eficienta de mult mai putin de 1% (!), in timp ce altele, cu randamente ce se apropie de 100%.
Exista cateva tipuri de mecanisme de excitatie:
a) pompare optica - excitatie de fotoni:
  In lasere medii active solide sau lichide ,este comuna furnizarea energiei de excitatie intr-o forma de radiatii electromagnetice (fotoni), care este absorbita in mediu activ.Sursa radiatiilor electromagnetice poate fi de diferite tipuri:
  - lampi flash, care sunt construite dintr-un tub de cuart, umplute cu gaz la joasa presiune. De obicei, xenon-ul este folosit, dar uneori atunci cand este necesar un aport mai mare de energie, alte gaze nobile cu masa atomica redusa, cum ar fi krypton sau heliu sunt folosite.
  - Un alt laser sau orice alta sursa de lumina
b) excitatia electrica a unui gaz:

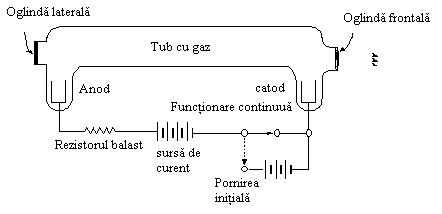
In cazul in care este mediul active este in stare gazoasa, cea mai buna este excitatia electrica de descarcare in gaze (vezi figura 3.11).
Gazul in tubu este neutru din punct de vedere electric, si atata timp cat nu este aplicata energetice din exterior, cea mai mare parte a moleculelor sunt in stare neutra. Cand , se aplica un current electric de inalta tensiune, electronii sunt eliberati de la catod si accelerati spre anod. Pe drum, acesti electroni intra in coliziune cu moleculele de gaz si transfera energie catre ei. Astfel, moleculele de gaz sunt ridicate la starea excitata.
  O tensiune mai mare este necesara pentru a incepe descarcarea electrica in tub decat pentru mentinerea descarcarii. Astfel, un prim impuls de inalta tensiune este aplicat pentru descarcarea initiala, si apoi tensiunea este redusa la valoarea de lucru.
Rezistenta de balast este folosita pentru a limita curentul in tub dupa ce descarcarea a avut loc. Cum conditiile de excitatie directa la gaze pentru a produce fenomenul laser sunt greu de gasit, o varianta acestei metode este folosita:
c) Coliziuni cu atomi
  Aceasta este cea mecanismul standard de excitatie in cu laserele comerciale cu gaze, cum ar fi laserul heliu-neon, sau laserul cu dioxid de carbon. In aceasta metoda cel putin doua gaye sunt in interiorul tubului. Un gaz primeste energie de la coliziunea cu electronii accelerati liber. Cel de-al doilea gaz primeste energie de la ciocnirile cu moleculelele excitate de la primul gaz.

Exemplu: laserul heliu-neon

Figura 3.12 arata graficul nivelului de energie la un laser heliu-neon, cu tranzitiile posibile. Masa de atomului de heliu este aproximativ o cincime din masa atomului de neon.Masa de heliu in tub este de aproximativ 6 ori masa de neon. Astfel atomii de heliu au mai multe sanse de a primi energie de la electronii accelerati, si se transfera in nivele excitate E3 si E5.

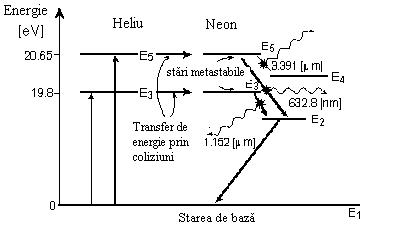
Figura 3.12. Diagrama nivelelor energetice ale laserului cu He-Ne

Atomul de neon are doua niveluri de energie (E3 si E5), care sunt foarte aproape de nivelurile de energie al atomului de heliu. Atomii excitati de heliu transfera energia lor de excitatie la atomii de neon prin coliziune - excitatie de rezonanta.
d) excitatie chimica
  In acest excitatie, energia este furnizata de o reactie chimica intre doi atomi sau molecule.
e) curentul electric in diode laser

Mecanismul de feedback

Mecanismul de feedback returneaza o parte din radiatia laser coerenta, care a fost creata in interiorul mediului activ, inapoi. De obicei, feedback-ul se face prin utilizarea oglinzilor plasate la ambele capete ale mediului activ. Aceste oglinzi sunt aliniate astfel incat radiatii se misca inainte si inapoi intre ele. In acest fel, o cavitate optica este creata.
De obicei, o oglinda reflecta in proportie de 100%, astfel incat toate radiatii care vin spre oglinda sunt reflectate inapoi la mediul activ. Celelalte oglinda este reflecta partial (10% - 99%), in functie de tipul de laser.Radiatiile care nu sunt reflectate inapoi in cavitatea optica, se transmise in afara laserului, si alcatuiesc fasciculul laser. Feedback-ul permite fiecarui foton sa treaca de mai multe ori prin mediul activ, deci va rezulta o amplificare puternica.Din cauza mecanismului de feedback, numai fotonii care circula intre oglinzi, raman in mediul activ, care ofera de directionalitatea fasciculului de iesire.

Cuplajul de iesire
Cuplajul este un mijloc de a transmite radiatiile electromagnetice din laser. de Cuplajul de iesire standard foloseste o oglinda care reflecta partial. Partea din fascicul, care nu este reflectata inapoi in activ mediu, este transmis afara. Intr-un fascicul laser continuu (in care se emit radiatii continuu), cea mai mare parte a radiatiilor este reflectata inapoi in cavitate si numai un mic procent este emis.In cazul anumitor laseri in puls marea majoritate a radiatiei din cavitate este transmisa intr-un puls la un moment dat.

Cavitatea optica, moduri de operare a laserului, componente optice
Unde stationare, moduri longitudinale,Curba de crestere, Moduri transversale,Cavitati optice laser, Criteriul de stabilitate, Numarul Fresnel, Oglinzi laser

Unde stationare

Cunoscute de la teoria ondulatorie, atunci cand doua unde similare cu aceeasi frecventa si amplitudine se deplaseaza in acelasi sens dar in directii opuse, interferenta lor creeaza o unda oscilatoare care apare ca si cum este fixa in spatiu - o unda stationara. In figura 4.1 este evidentiata aparitia unei unde stationare pe parcursul unui ciclu complet.

Figure 4.1: Producerea undelor stationare din doua unde care se deplaseaza in directii opuse

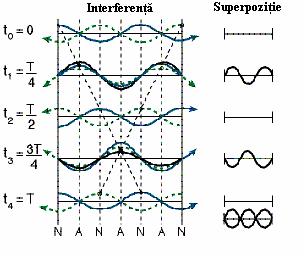
In figura 4.1 este descrisa fiecare 1 / 4 din ciclu a undei.Punctul negru arata cum perturbare varfului undei avanseaza in timpul unei perioade complete, T.Linia groasa descrie o una care se deplaseaza spre dreapta. Pe partea dreapta a figura 4.1 se afiseaza suprapunerea celor doua valuri. Ca o unda stationara intr-un sir incastrata in puncte fixe la ambele parti,punctele fixe ale unei unde stationare sunt numite noduri. Distanta dintre nodurile adiacente, este de o jumatate de lungime de unda a fiecarei unde de interferenta. Astfel, aceasta este la fel ca o jumatate de lungime de unda a undei stationare pe care o creeaza.

Unde stationare in laser

Intr-un laser cavitatea optica este creata de doua oglinzi la ambele capete ale laserului (oglinzi laser). Aceste oglinzi servesc la doua obiective:
1. Maresc lungimea mediului activ, prin trecerea fasciculului de mai multe ori prin el.
2. Ele determina conditiile-limita pentru campurile electromagnetice din interiorul cavitatii laser.
O cavitate cu doua oglinzi se numeste rezonatorul Fabry-Perot. Axa care este in prelungirea centrelor oglinzilor si perpendiculara pe ele se numeste axa optica a laserului. Fascicul laser este emis din laser in directia axei optice.
O unda electromagnetica care misca in interiorul cavitatii laser de la dreapta la stanga, este reflectata de oglinda din stanga catre oglinda din dreapta, si asa mai departe. Astfel, doua unde de aceeasi frecventa si amplitudine se misca in directii opuse, care este conditia de creere a undei stationare.Undele electromagnetice din interiorul cavitatii laser sunt 3D, si se misca de-a lungul axei optice a laserului.

Conditii pentru unde stationare

Pentru a creea unde stationare, unda trebuie sa inceapa cu aceeasi faza la oglinda. Astfel, calea optica de la o oglinda la alta si inapoi si trebuie sa fie un numar intreg de multiplicare a lungimii de unda. Avand in vedere ca lungimea dintre oglinzi este constanta L, lungimile de unda potrivite, care creeaza unde stationare, trebuie sa indeplineasca urmatoarele conditii:

L - lungimea cavitatii optice.
m - numarul modulului, care este egal cu numarul de jumatati de lungimi de unda din interiorul cavitatii optice. Primul modul contine o jumatate de lungime de unda, cel de-al doilea contine doua jumatati de lungime de unda.
m - lungime de unda del modul m in interiorul cavitatii laser.
l_m -lungimea de unda a modului m din interiorul cavitatii laser.Lungimea de unda a modului laser   l_m este masurata in interiorul mediului activ.
Lungime de unda ,in fond, este egala cu:

l - lungimea de unda a luminii in vid.
    n - indicele de refractie al mediului activ.
  c - viteza luminii in vid.
Am observat ca frecventa de lumina ramane aceeasi in vid sau in diferite materiale, numai lungimea de unda se schimba.

Lungimea de unda l_m poate fi exprimata ca:

unde c / n este viteza luminii intr-un anumit mediu cu indicele de refractie n.
Si, de la (4.3), frecventa modului longitudinal este:

Introducand l_m din 4.1 in ultima ecuatie obtinem:

Primul mod de oscilatie valabil pentru cavitatea optica este:

Acest mod este numit modul longitudinal de baza, si are frecventa cavitatii optice.
Frecventa fiecarui mod laser este egal cu numarul intreg din inmultirea lui m cu frecventa modului longitudinal de baza. Diferenta intre frecventele de baza a modurilor adiacente este egala cu frecventa de baza din cavitatea optica:

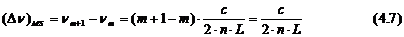
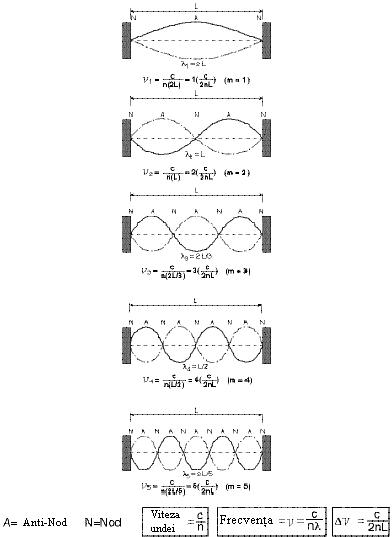
Unde stationare intr-un sir

In figura 4.2 primele 5 unde stationare sunt ilustrate.

	Figura 4.2: Modurile longitudinale intr-o cavitate de lungime L

Acestea sunt echivalente cu modurile laser longitudinale, care sunt modurile de-a lungul axei optice a laserului.
L - lungimea cavitatii optice.
n - indicele de refractie.
m - numarul de modul, care este egal cu numarul de jumatati de lungimi de unda din interiorul cavitatii optice.
l_m - lungimea de unda a modului m, care este egal cu numarul de jumatati de lungimi de unda din interiorul cavitatii.
Conditia necesara pentru aceste unde stationare este un nod la fiecare capat (oglinda).

Pana in prezent s-a asumat faptul ca indicele de refractie (n) este constant de-a lungul cavitatii optice. Acest lucru inseamna ca, lungimea mediului activ este egal cu lungimea cavitatii optice. Exista lasere in care oglinzile nu sunt la capetele mediului activ, asa ca L1 nu este egal cu lungimea cavitatii (L). In acest caz, fiecare sectiune a cavitatii este calculata separat, cu propriile sale indice de refractie:

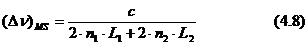
In spectrul vizibil,pentru cavitati de zeci de centimetri lungime modul m este foarte mare, de ordinul milioanelor. De fapt, acesta va fi explicat faptul ca nu toate modurile posibile in functie de formula vor aparea in fascicul laser, pentru ca exista o multime de conditii limita.

Frecvente permise in interiorul unei cavitati laser

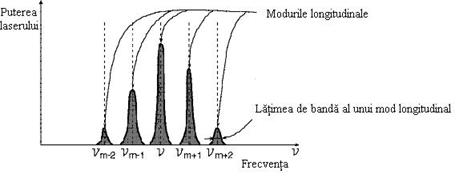
In Figura 4.3 este o reprezentare grafica a frecventelor permise intr-o cavitate laser.

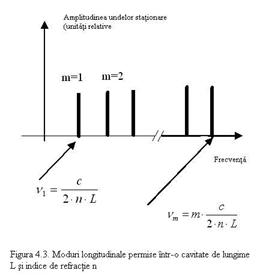
In practica, frecventele nu sunt definite matematic ca frecvente singulare, dar fiecare are o latime de banda in jurul modurilor posibile. Nu toate aceste frecvente vor fi emise de laser, deoarece exista mai multe conditii de limitare.
Modurile longitudinale in lasere sunt unde stationare de-a lungul axei optice a laserului. Undele stationare se formeaza atunci cand doua unde cu aceeasi frecventa si amplitudine se deplaseaza in sens opus. Doua oglinzi la ambele capete ale laserului creeaza cavitatea optica. Undele stationare din interiorul unei cavitati laser sunt create atunci cand radiatiile electromagnetice sunt nevoite sa se intoarca inapoi in cavitate de catre oglinzi.
Frecvente permise in interiorul unei cavitati optice sunt determinate de lungimea de cavitate (L) si indicele de refractie al mediului activ. Numai acele frecvente, care creeaza noduri la ambele oglinzi, sunt permise. Astfel, lungimea cavitatii trebuie sa fie un numar intreg de multiplicare a jumatatii lungimii de unda.

Frecventele permise sunt distantate la un interval constant, care este egal cu frecventa de baza a cavitatii.
Doar anumite frecvente sunt posibile in interiorul cavitatii optice a unui laser, in functie de conditia undei stationare. Din toate aceste frecvente posibile, numai cele care au amplificarea peste un anumit prag, pentru a invinge absorbtia(cum va fi explicat in capitolul 5) vor fi emise de laser. Acest minim de amplificare este definit ca pragul de "lasing".
Conditia minima de amplificare inseamna ca amplificarea este egala cu pierderile, pentru ca intr-un drum dus-intors in interiorul cavitatii G_L = 1.

Curba de crestere a mediului activ

In figura 4.4 este prezentata curba de randament al mediului activ, ca o functie de frecventa, marcata de pragul procesului laser si modurile longitudinale posibile.

Figura 4.4: Curba de randament a unui laser

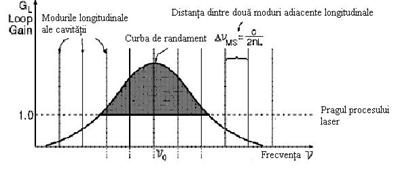
Inaltimea fiecarei linie depinde de pierderile intr-un drum dus-intors in interiorul cavitatii, inclusiv a radiatiilor emise. Forma si proprietatile curbei de randament este explicata in capitolul 5. Regiunea marcata de sub curba si mai sus de pragul lasing include zona unde fenomenul laser poate aparea.
Inaltimea curbei depinde de lungimea mediului activ si de excitatia sa.Modurile longitudinale posibile sunt marcate ca linii perpendiculare la distante egale una de alta. In sectiunea 4.1 conditia undelor stationare pentru moduri longitudinale a fost determinata de lungimea cavitatii si indicele sau de refractie. In figura 4.4 doar 5 frecvente din cele permise in interiorul cavitatii, sunt mai sus de pragul lasing. Astfel, numai aceste 5 frecventelor pot exista la iesirea din acest laser.

	Figura 4.5: Distributia spectrala a liniilor laser.

Numarul de moduri longitudinale optice

In figura 4.5 distributia spectrala a liniilor emise de laser este descrisa in figura 4.4. In acest laser 5 frecvente sunt permise, la iesire, si sunt asezate la distante egale, care sunt egale cu modul de distantiere:

Latimea liniei de fluorescenta dn_LW a unui laser

Curba de crestere este o reprezentare grafica a cresterii, in functie de frecventa si descrie latimea liniei de fluorescenta.Latimea liniei de fluorescenta dn_LW a laserului este latimea de amplificare a curbei la jumatate din inaltimea maxima. Aceasta latime a liniei de fluorescenta determina latimea maxima a tuturor liniilor emise de laser (radiatie coerenta la iesirea din laser, la toate modurile longitudinale posibile). Explicarea detaliata poate fi gasita in capitolul 5. Numarul aproximativ de moduri posibile (N) este dat de latimea liniei de fluorescenta impartita la distanta dintre modurile adiacente:

MS - Modul de spatiere.
   LW - latimea liniei.
dn_LW - latimea linie fluorescente .
Dn_MS - distanta dintre modurile longitudinale adiacente.

Controlarea numarulului de moduri longitudinale ale laserului

Pentru a controla numarul de moduri longitudinale intr-un laser trebuie controlata lungimea cavitatii laser. Acest lucru poate fi realizat in doua moduri:
1.Modificarea lungimii cavitatii prin deplasarea oglinzilor. Dublarea lungimii cavitatii reduce la jumatate distanta dintre modurile longitudinale adiacente, astfel, dubland numarul de moduri laser posibile sub curba fluorescentei. Este clar ca un singur mod laser se poate face prin reducerea lungimii cavitatii, astfel ca numai un singur mod longitudinal va ramane sub curba cu fluorescenta G_L> 1. In acest mod laser, distanta dintre oglinzi este critica, deoarece, daca nu va exista nici moduri pentru a indeplini aceasta stare, nu se va produce fenomenul laser. Dezavantajul este ca aceasta metoda de a scurta lungimea cavitatii limiteaza puterea de iesire a laserului.
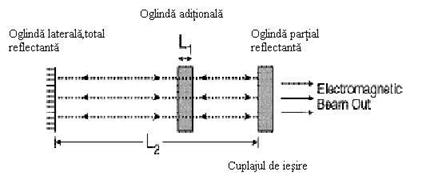
2. Adaugarea de o oglinda in interiorul cavitatii laser.
  Adaugarea unei oglinzi in interiorul cavitatii laser este descrisa in figura 4.6.
Aceasta metoda determina doua lungimi ale cavitatii in acelasi timp: L1 si L2.
Lungimea L1 este aleasa in asa fel incat doar un singur mod longitudinal va fi sub cu curba de fluorescenta laser.
De laser ca are nevoie de un sistem de a-si indeplini conditiile pentru ambele carii.
Acest aranjament necesita pozitii stabile pentru oglinzi, si este folosita oriunde este necesara putere mare intr-un singur mod, in special in laserii cu medii active solide.

  

Figure 4.6: Operarea unui laser intr-un singur mod cu trei oglinzi.

Diferenta dintre Modurile Adiacente Longitudinale.

Desi cele mai multe lasere opereaza in mai multe moduri longitudinale, noi inca le privim ca surse monocromatice. Diferenta dintre doua moduri adiacente este foarte mica. Avand in vedere un laser He-Ne care are l_m = 632.8000 nm pentru modul m,modul (m+1) va avea l_m+1 = 632.7996 nm.Diferenta in lungimi de unda intre modurile longitudinale adiacente este de 4*10^-13metri, astfel incat putem sa consideram un astfel de laser monocromatic in cele mai multe aplicatii practice.

Importanta modurilor longitudinale optice la iesirea din laser

Importanta modurilor longitudinale optice la iesirea din laser este determinata de aplicatia specifica a laserului.
    1. In aplicatiile cu cele mai mari puteri de iesire, pentru prelucrarea materialelor sau interventii chirurgicale, laserul este utilizat ca un mijloc de transfer al energiei la tinta. Astfel, nu exista nici o importanta pentru modurile longitudinale laser.
    2. In cazul in care cererile de interferenta a radiatiilor electromagnetice sunt importante, cum ar fi holografia sau masuratorile interferometrice, modurile longitudinale sunt foarte importante.
In aceste aplicatii, lungimea de coerenta a radiatiei este o proprietate importanta, si este determinata de latimea liniei de radiatie laser (invers proportionala cu acesta). In aceste aplicatii un singur modul laser este utilizat, si tehnici speciale sunt utilizate pentru a reduce latimea liniei, marindu-i astfel lungimea de coerenta.
    3. In spectroscopie si aplicatiile fotochimice, este necesara o lungime de unda foarte bine definita. Acest lucru se realizeaza prin functionarea laserului intr-un singur mod, si controlarea lungimii cavitatii, astfel va functiona la exact lungime de unda necesara. Structura de moduri longitudinale laser este critica pentru aceste aplicatii.
4. Cand sunt necesare impulsuri scurte de mare putere, modul de blocare este utilizat. Acest proces provoaca interferente constructive intre toate modurile din interiorul cavitatii laser. Structura de moduri longitudinale laser este importanta pentru aceste aplicatii.

Modurile laser

In interiorul unei cavitati laser modurile sunt caracterizate prin:
1. Frecventa (n), sau lungime de unda (l

Modurile transversale ale unui laser

In sectiunile anterioare distributia intensitatii a fost examinata de-a lungul axei optice a laserului.Modurile longitudinale au fost descrise ca fiind unde stationare intre oglinzile laser. Aceasta sectiune analizeaza distributia transversala de intensitate, in sectiunea transversala a fasciculului, perpendicular pe axa optica a laserului. Aceste moduri transversale sunt create de adancimea cavitatii, care permite cateva moduri 'diagonale' sa se dezvolte in interiorul cavitatii laser. Un pic de nealiniere a oglinzilor cauzeaza diferite raze sa aibe drumuri diferite in interiorul cavitatii. Astfel, distributia de intensitati nu este o distributie perfect Gaussiana.

Forma modurilor transversale electromagnetice

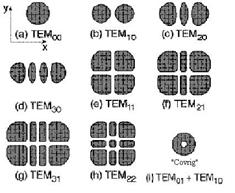
In sectiune transversala,radiatia laser are o distributie specifica in anumite regiuni cu un grad ridicat de intensitate si regiuni fara radiatie. Figura 4.7 arata distributia energiei de la primele cateva moduri transversale electromagnetice.Zonele intunecate marcheaza locurile in care a lovit radiatia laser.

Figure 4.7: Moduri tranvsersale electromagnetice

In cazul in care puterea de iesire a laserului este de ordinul de cativa wati, distributia de energie in sectiunea transversala a fasciculului poate fi masurata printr-o scurta iluminare a unui bat de lemn. Pentru puteri mici pot fi utilizate ecrane speciale, care raspund la anumite lungimi de unda ale laserului. Ecranul isi schimba proprietatile in locurile expuse la fascicul laser, si o imagine similara este figura 4.7. Forma de distributie a energiei in sectiunea transversala a fascicul se numeste: Moduri Electro-Magnetice Transversale (MET).
Modurile Electro-Magnetice Transversale (MET) descriu forma de distributie a energiei in sectiunea transversala a fasciculului. Figura 4.7 arata distributie de energie a primelor cateva moduri transversale electromagnetice.Zonele intunecate marcheaza locurile in care a lovit radiatia laser. Fiecare modul transversal (TEM) este marcat cu doi indici: TEM_mn.
m, n, sunt numere intregi. Presupunand ca fascicul avanseaza in directia z:
m - numarul de puncte zero iluminate (intre regiuni iluminate) de-a lungul axei x.
n - numarul de puncte zero iluminare (intre regiuni iluminate) de-a lungul axei y.
Exista un singur mod transversal, care nu se incadreaza in aceasta clasificare, si are o denumire speciala (in functie de forma), ca urmare a importantei sale: 'Covrig'. Acesta este compus din MET₀₁ si MET₁₀ osciland impreuna (a se vedea figura 4.7).

Distributia campului electric al modurilor MET

Intensitatea radiatiei laser, este o masura a patratului campului electric a radiatiilor electromagnetice.

Figura 4.8: Intensitatea si campul electric al catorva moduri transversale

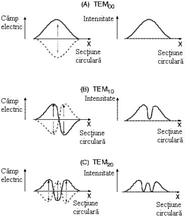
Regiunile intunecate din figura 4.7 sunt zonele cu un grad ridicat a campului electric. In figura 4.8 atat intensitatea cat si campul electric sunt afisate pentru cateva moduri transversale.

Controlul modurilor transversale ale laserului

Atunci cand un laser functioneaza in mai multe moduri transversale,intensitate totala este o suprapunere a tuturor modurilor transversale existente. Figura 4.9 descrie distributia de intensitate a 3 moduri inferioare, si suprapunerea lor. Figura 4.9 indica faptul modul transversal inferior TEM₀₀ are cel mai mic diametru in comparatie cu alte moduri. Acest lucru da un indiciu despre cum se face un laser sa unctioneze intr-un singur mod transversal de baza: se prelucreaza un orificiu circular cu diametrul potrivit in interiorul cavitatii optice. Prin alegerea diametrului egal cu diametrul modului inferior, numai acest mod poate trece prin orificiu, si restul modurilor superioare sunt attenuate . Deoarece radiatiile optice in interiorul cavitatii sunt intr-o miscare rapida, numai modul de baza va fi amplificat, si va fi emis.

Figura 4.9: Radiatia laser cu cateva moduri transversale.

Caracteristicile Modului Transversal Fundamental (TEM₀₀) din Laser

Distributia de intensitati ale modului transversal fundamental are forma unei curbe matematice numita 'Gaussiana'. Modul transversal fundamental este singurul mod in care toate radiatiile sunt in faza de-a lungul sectiunii transversale a fasciculului (a se vedea figura 4.8).

Descrierea matematica a distributiei de intensitati in functie de distanta de la centru, este:

I₀ - intensitatea in centrul fascicululului (intensitatea maxima)

r - raza fasciculului Gaussian.Aceasta este distanta din centru, unde intensitatea coboara la 1/e² din intenistatea maxima.Puterea maxima a fasciculului Gaussian este:

Se poate demonstra ca unghiul de divergenta a fasciculului Gaussian este:

Modul transversal fundamental are proprietati care il fac foarte practic,si producatorii incearca sa construiasca lasere, care opereaza in modul fundamental Gaussian.



Proprietati Modului Transversal Gaussian

Cel mai mic unghiu de divergenta decat toate celelalte moduri transversale.
Pot fi concentrate intr-un spot, mai mic decat la toate celelalte moduri transversale.
Are cea mai buna coerenta spatiala in raport cu alte moduri transversale.
Distributia spatiala a unui fascicul Gaussian ramane Gaussian in timp ce fasciculul se propaga prin spatiu.

Imagistica cu o lentila a unui fascicul Gaussian, precum si alte elemente optice,prin care trece fasciculul, creeaza din nou, un fascicul Gaussian.

Cavitatea Optica

In fiecare cavitate laser exista (cel putin) doua oglinzi la capetele laserului. Aceste oglinzi sunt indreptate una spre cealalta, si centrele lor sunt pe axa optica a laserului. Distanta dintre oglinzi determina lungimea cavitatii optice a laserului (L). Exista diferite forme de oglinzi, cu lungimi diferite intre ele. O cavitate optica este determinata de mediul activ utilizat, puterea optica, si de aplicatie specifica.
Explicatia de aici va rezuma principiile de proiectare a unei cavitati optice:
  Definitii importante.
  Pierderile din interiorul cavitatii optice.
  Cavitati optice comune
  Criteriul de stabilitate a cavitatilor laser

Definitii importante pentru cavitatea optica:

Cavitatea optica - cavitatea laser - regiunea dintre oglinzile laserului.
Axa optica - linie imaginara care leaga centrele oglinzilor, si este perpendiculara pe ele. Axa optica este in mijlocul cavitatii optice.
Diafragma - factorul care limiteaza diametrul fasciculului din interiorul cavitatii laser. De obicei, este determinata de diametrul de mediului activ, dar in unele lasere un orificiu circular se prelucreaza in cavitatea laser pentru a limita diametru fasciculului. Un exemplu este limitarea deschiderii pentru realizarea laser cu functionarea intr-un singur mod.

Pierderile din interiorul cavitatii optice - include toate radiatii care lipsesc de la iesirea din laser (emise prin cuplajul de iesire). Amplificarea din mediul activ trebuie sa depaseasca aceste pierderi.

Pierderi in interiorul cavitatii optice

Nealinierea oglinzilor laser - Cand oglinzile nu sunt exact aliniate perpendicular pe axa laserului, precum si paralel intre ele (simetric), radiatiile din interiorul cavitatii nu vor fi limitate in timpul calatoriei intre oglinzi.
Absorbtia, dispersia si pierderile cauzate de elementele optice - Deoarece elementele optice nu sunt ideale, fiecare interactiune cu un element optic din interiorul cavitatii cauzeaza unele pierderi.
Pierderi datorate difractiei- de fiecare data cand un fascicul laser trece printr-un orificiu limitator se petrece fenomenul difractiei. Nu este intotdeauna posibil modificarea orificiului pentru reducerea difractiei. Ca un exemplu, o astfel de crestere va genera un fascicul laser in moduri de transversale superioare, care nu sunt dorite.

Cavitati optice specifice

Fiecare cavitate optica are doua oglinzi la capete cu raze de curbura R1 si R2. Regiunile din interiorul mediului activ, care nu sunt incluse in mediul activ, nu participa la producerea fascicului laser. Doi parametrii determina structura din cavitatea optica:
1. Volumul modului laser din interiorul mediului activ.
2. Stabilitatea cavitatii optice.
In paginile urmatoare, fiecare tip de cavitate optica este descrisa.Regiunile intunecare din fiecare cavitate optica marcheaza volumul modului activ in acea cavitate.

a. Cavitatea optica plan paralela.

Figura 4.10 descrie cavitatea optica plan paralela

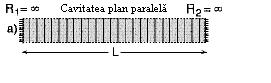
La ambele capete sunt doua oglinzi plane (R₁ = , R₂ = ) paralele intre ele si perpendiculare pe axa optica a laserului.
Avantaje:
Utilizarea optima intregului volum al mediului activ. Astfel, este folosit in cadrul laserilor in puls, care au nevoie de un maximum de energie.
Nu concentreaza radiatia laser in interiorul cavitatii optice. In cadrul laserilor de mare putere aceasta concentrare poate provoca caderi electrice sau poate deteriora elementele optice.
Dezavantaje:
Pierderi mari datorita difractiei.
Sensibilitate foarte mare la nealiniere. Astfel, este foarte dificila operarea cu un astfel de laser.

b.Cavitatea circular concentrica.

Figura 4.11 descrie cavitatea circular concentrica.

La ambele capete sunt doua oglinzi sferice cu aceleasi raze. Distanta dintre centrele oglinzilor este egala cu de doua ori raza de curbura a fiecaruia dintre ele (R1 = R2 = L / 2). Acest aranjament cauzeaza o concentrare a fasciculului la centrul cavitatii. Proprietatile acestei cavitati sunt opuse de cele ale cavitatii plan paralele:

Avantaje:
Sensibilitate foarte mica la nealiniere. Astfel, se aliniaza foarte usor.
Pierderi foarte mici cauzate de difractie.
Dezavantaje:
Utilizarea limitata a volumului mediului activ. Este utilizat in de pomparea optica continua a laserilor cu care au ca mediu activ colorant organic (vezi pct. 6.4). In aceste lasere colorantul lichid curge in directia fasciculului (directia de curgere este perpendiculara pe axa optica a laserului).Astfel,este nevoie de o mare densitate de putere pentru a pompa colorantul.

Concentrandu-se radiatia laser in interiorul cavitatii optice poate provoca descarcari electrice sau poate deteriora elementele optice.

c. Cavitatea confocala.
Figura 4.12 descrie cavitatea confocala

Aceasta cavitate este un compromis intre cavitatea plan paralela si cele circulare. La ambele capete sunt doua oglinzi sferice cu aceeasi raza. Distanta dintre centrele oglinzilor este egala cu raza de curbura a fiecareia dintre ele (R1 = R2 = L). Acest aranjament produce o concentrare mult mai mica a fasciculului in centru cavitatii.
Avantaje:
Sensibilitate redusa la nealiniere. Astfel, se aliniaza foarte usor.

Pierderi scazute datorita difractiei.
  Concentrare redusa in centrul cavitatii.
Utilizare medie a volumului mediului activ.
Principala diferenta intre cavitatea confocala si cea sferica este ca, in cavitatea confocala punctul focal al fiecarei oglinzi se afla in centrul cavitatii, in timp ce in cavitatea sferica centrul de curbura al oglinzilor se afla in centrul cavitatii.

d. Cavitatea cu raza de curbura a oglinzilor mult mai mare decat lungimea cavitatii.

Figura 4.13 descrie cavitatea cu raza de curbura a oglinzilor mai mare decat lungimea cavitatii.

	Figure 4.13: Cavitatea cu raza mare de curbura

Aceasta cavitate este un compromis mai bun decat cavitatea confocala intre cavitatea plan paralela si cavitatile optice circulare. La ambele capete sunt doua oglinzi sferice raza mare de curbura (nu este nevoie sa fie la fel). Distanta dintre centrele a oglinzilor este cu mult mai mica decat raza de curbura a fiecareia dintre ele (R1, R2>> L). Acest aranjament diminueaza concentrarea fasciculului in centrul cavitatii.
Avantaje:
  Sensibilitate medie la nealiniere.
  Pierderi medii la difractii

Lipsa unei concentrari puternice a fasciculului in centrul cavitatii.
  O buna utilizare a volumului mediului activ


e. Cavitatea emisferica.

Figura 4.14 descrie cavitatea emisferica.Cavitatea este creata dintr-o oglinda plana, si o oglinda sferica cu raza de curbura egala cu lungimea de cavitate.

	Figura 4.14: Cavitatea emisferica.

Aceasta cavitate este similara cu cavitatea confocala, cu avantajul pretulului redus a oglinzii plane.

g.Rezonatorul Instabil.

Figura 4.16 descrie un exemplu de cavitate instabila. Un exemplu de astfel de cavitate este determinat de un aranjament convex-concav a oglinzilor sferice.

Figura 4.16: Cavitate instabila

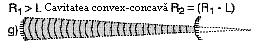
Oglinda concava este mare la fel si raza de curbura, care este mai mare decat lungimea cavitatii.Oglinda convexa este mica si raza ei de curbura este mica. Intr-o astfel de cavitate modelul unor unde stationare nu este creat in interiorul cavitatii.Radiatiile nu parcurg acelasi traseu intre oglinzi. Raza de curbura a ambelor oglinzi se intalneste in acelasi punct.
Avantaje:
Volum mare de moduri laser in interiorul mediului activ.
Toata puterea din interiorul cavitatii este emisa din laser, nu doar o mica parte.
Radiatia laser este emisa din laser in jurul marginilor oglinzii mici.
Aceasta cavitate este utilizata in lasere de mare putere, care nu pot folosi un cuplaj de iesire standard.
Dezavantaje:
Fasciculul are forma unui cerc in mijloc.



Criteriul de stabilitate a cavitatii

O cavitate stabila este o cavitate in care a radiatia este capturata in interiorul cavitatii, creand unde stationare in timp ce fasciculul se deplaseaza intre oglinzi.Geometria cavitatii determina cazul in care cavitatea este stabila sau nu. Este posibil sa utilizam rezonatorul instabil numai in cazul in care mediul activ are un randament mare, avand in vedere ca fasciculul trece prin mediul activ de mai putine ori decat in cavitatea stabila. Pentru determinarea stabilitatii, un criteriu de stabilitate trebuie sa fie definit. Mai intai un parametru geometric este definit pentru fiecare dintre oglinzi:

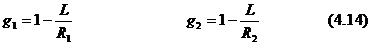
g₂ = 1 - L/R₂

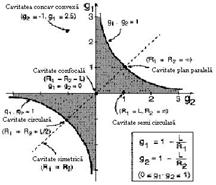
O reprezentare grafica a parametrilor geometrici este prezentata in figura 4.17.

Figure 4.17: O reprezentare grafica a parametrilor geometrici

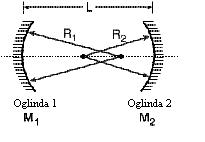
O cavitate este stabila daca: 0 < g₁· g₂ < 1 (4.15)

Diagrama de stabilitate


O cavitate este stabila in cazul in care centrul de curbura a uneia dintre oglinzi, sau pozitia sa, dar nu a amandorura, este intre cea de-a doua oglinda si centrul ei de curbura. In graficul de stabilitate parametrii geometrici a oglinzilor sunt axele x si y. Figura 4.18 arata diagrama de stabilitatea a tuturor cavitatilor laser. In diagrama de stabilitate, in figura 4.18, zona intunecata marcheaza zona de stabilitate. Stabilitatea regiunii este inconjurata de doua hiperbole definite de criteriul de stabilitate. Cateva cavitati comune sunt marcate pe diagrama de stabilitate.Acordati o atentie speciala pentru cavitatile laser care se afla pe marginea regiunii de stabilitate! Pentru aceste cavitati, produsul g₁ . g₂ este fie '0' sau '1'.

Figure 4.18: Diagrama de stabilitate a cavitatilor laser

Numarul Fresnel

Daca un rezonator stabil functioneaza intr-un mod de ordin mic sau mare, depinde in mare parte de marimea efectiva a deschiderii in raport cu lungimea cavitatii.
  Un laser cu mediu active gazos cu o constructie lunga si ingusta va tinde sa opereze intr-un ordin scazut, din cauza atenuarii a celor mai mari moduri de catre peretii interiori ai tubului.
Modurile mai mari sunt asociate cu o difractie sau cu un unghi de divergenta mare,care sunt atenuate de o deschidere limitata.
O masura a tendintei unei cavitati laser stabile de a opera intr-un ordin inferior sau superior, este data de numarul Fresnel:

unde a este raza efectiva a deschiderii,care ar trebui sa fie considerata cea mai mica raza de deschidere a sistemului, daca aceasta nu este prea departe de una din oglinzi.
Intr-un sistem in care singura limitare este datorata oglinzilor, presupunand ca au razele egale (a² = a_1·a₂, in cazul in care a₁ si a₂ sunt cele doua raze ale oglinzilor) numarul Fresnel reprezinta numarul de zone Fresnel interceptate de catre una din oglinzi in cazul in care o unda plana lumineaza cealalta oglinda.
O valoare mai mica sau egala cu 1 a numarului Fresnel rezulta o operare in cel mai mic mod, TEM₀₀.

Domeniul departat al divergentei

Pentru un fascicul Gaussian, diametrul fasciculului la o distanta z este dat de (Kogelnik si Li, Fascicule Laser si Rezonatoare, Aplicatii Optice 5, oct.1966):

unde w₀ este raza spotului la z=0 si z_R = pw₀/l,domeniul Rayleigh.Pentru z>>1

Divergenta la departare este data de raportul: