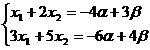Fie sistemul de m
ecuatii si n necunoscute:
 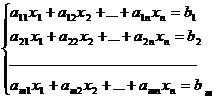 (1) (1)
Unde 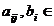 r r 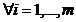 si si 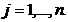 Daca Daca 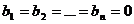 sistemul (1) se
numeste omogen. sistemul (1) se
numeste omogen.
Sistemul (1)
poate fi scris condensat sub forma:
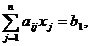 1 1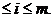
Coeficientii necunoscutelor formeaza o matrice cu m linii si n coloane:
A= 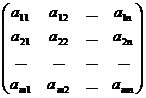
numita matricea
coeficientilor sistemului sau,
simplu, matricea sistemului. Matricea cu m linii si n+1 coloane
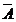 = =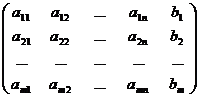
Care se obtine adaugand la coloanele matricei A coloana
termenilor liberi 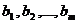 , se numeste matricea
extinsa a sistemului. , se numeste matricea
extinsa a sistemului.
Un
sistem de numere 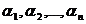 se numaste solutie a sistemului (1), daca inlocuind necunoscutele se numaste solutie a sistemului (1), daca inlocuind necunoscutele 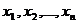 respectiv prin
aceste numere, toate solutiile acestui sistem sunt verificate, adica respectiv prin
aceste numere, toate solutiile acestui sistem sunt verificate, adica
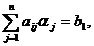 1 1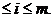
Un sistem de ecuatii care nu are solutii se
numeste incompatibil.
Un sistem de ecuatii liniare care are cel putin o
solutie se numeste compatibil. Un
sistem compatibil se numeste determinat daca are o singura solutie, si se
numeste nedeterminat daca are mai
mult decat o solutie.
In legatura cu sistemele de ecuatii liniare ne punem
problema stabilirii unor metode care sa ne permita sa decidem daca un sistem
de ecuatii dat este compatibil sau nu, iar in cazul in care este compatibil,
sa putem spune daca este determinat sau nu, si sa dam procedee de gasire a
tuturor solutiilor sale.
Pentru
rezolvarea unui sistem de ecuatii liniare de n ecuatii cu n necunoscute,
care au determinantul sistemului nenul, avem urmatoarea teorema:
Teorema ( Regula lui Cramer ). Daca d=detA
este nenul, atunci sistemul (1) are o solutie unica, anume:
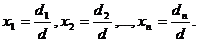
In
concluzie, un sistem de n ecuatii
liniare cu n necunoscute, al carui determinant este nenul, este compatibil determinat, iar solutia sa
este data de formulele lui Cramer.
Aplicatie. Sa se rezolve sistemul
de ecuatii liniare
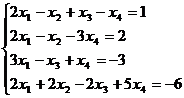
Rezolvare. Determinantul sistemului
d = 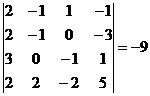
fiind nenul, solutia este data de formulele lui Cramer.
Valorile necunoscutelor vor avea la numarator
determinantii:
d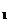 = =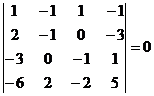 , d , d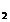 = =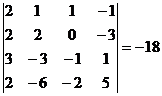
d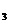 = =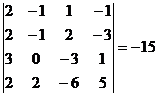 , d , d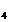 = =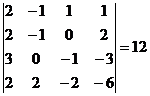
Astfel, 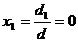 , , 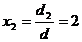 , , 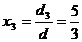 , , 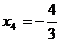 este solutia
sistemului nostru; mai mult , aceasta
este unica solutie. este solutia
sistemului nostru; mai mult , aceasta
este unica solutie.
Cazul
general
Fie un sistem
de ecuatii liniare, cu m ecuatii si
n necunoscute, cu m diferit de n:
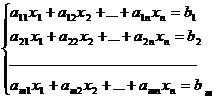 (1) (1)
Ne punem
mai intai problema compatibilitatii sistemului (1). Pentru aceasta, sa
analizam matricea A a coeficientilor sistemului si matricea extinsa 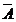 , care se obtine din A
completand coloanele sale cu coloana termenilor liberi ai sistemului (1), , care se obtine din A
completand coloanele sale cu coloana termenilor liberi ai sistemului (1),
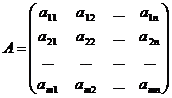 , , 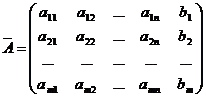 . .
Este evident ca 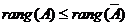 , deoarece minorii matricei A se gasesc printre minorii matricei , deoarece minorii matricei A se gasesc printre minorii matricei 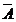 . .
Problema compatibilitatii sistemelor de ecuatii liniare
este rezolvata de urmatoarea teorema:
Teorama lui Kronecker-Cappelli. Un
sistem de ecuatii liniare (1) este compatibil daca si numai daca rangul matricei sistemului A este egal cu rangul matricei extinse 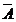 . .
Utilizarea acestei teoreme, in exemple concrete,
necesita inainte de toate, calculul rangului matricei A. Pentru aceasta trebuie sa gasim un minor nenul al lui A , fie acesta d, astfel incat toti minorii care contin pe d sa fie nuli. Orice minor de acest fel il vom numi minor principal. Apoi, este suficient
sa verificam ca orice minor al matricei A
, care contine pe d si care nu este minor al lui A , este de asemenea nul. Orice astfel
de minor de ordin r+1, obtinut prin bordarea unui minor principal cu
elementele corespunzatoare ale coloanei termenilor liberi, precum si cu cele
ale uneia dintre liniile ramase, se numeste minor caracteristic.
Astfel,
teorema lui Kronecker-Capelli se poate enunta si sub forma urmatoare:
Teorema lui Rouché . Un sistem de ecuatii (1) este compatibil daca si numai
daca toti minorii caracteristici sunt nuli.
Sa presupunem acum ca sistemul (1) este compatibil.
Teorema lui Kronecker-Capelli ne permite sa decidem daca sistemul este
compatibil sau nu, dar nu ne da un mijloc practic de aflare a tuturor solutiilor sistemului dat.
De aceasta problema ne vom ocupa in continuare.
Fie
deci un sistem de ecuatii liniare (1) compatibil. Sa presupunem ca rangA=rang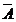 =r si ca un minor principal al sistemului se gaseste la
intersectia primelor r linii si a
primelor r coloane, adica =r si ca un minor principal al sistemului se gaseste la
intersectia primelor r linii si a
primelor r coloane, adica
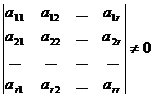 . .
Dupa
cum am observat orice linie a matricelor A si 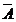 este combinatie
liniara de primele r linii. De aici rezulta ca orice ecuatie a
sistemului (1) este o combinatie
liniara de primele r ecuatii ale sistemului (1) este o combinatie liniara de
primele r ecuatii ale sistemului (1), cu anumiti coeficienti. De aceea, orice
solutie a primelor r ecuatii satisface toate ecuatiile sistemului (1). Este
suficient deci sa rezolvam sistemul este combinatie
liniara de primele r linii. De aici rezulta ca orice ecuatie a
sistemului (1) este o combinatie
liniara de primele r ecuatii ale sistemului (1) este o combinatie liniara de
primele r ecuatii ale sistemului (1), cu anumiti coeficienti. De aceea, orice
solutie a primelor r ecuatii satisface toate ecuatiile sistemului (1). Este
suficient deci sa rezolvam sistemul
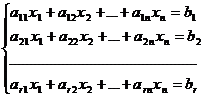 (5) (5)
care este echivalent cu sistemul (1).
Matricea
coeficientilor sistemului (5) are un minor nenul de ordin r ( format din
primele r coloane) si deci are rangul egal cu r, unde r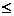 n. Distingem doua cazuri: n. Distingem doua cazuri:
1. Daca r = n,
sistemul (5) are acelasi numar de ecuatii si de necunoscute, iar
determinantul sau este nenul. In acest caz, acest sistem are o solutie unica
pe care o putem calcula cu formulele lui Cramer. Aceasta este si solutia
sistemului (1).
2. Fie r<n. Pentru a fixa ideile, vom
presupune ca mai inainte, ca minorul format din coeficientii primelor r
necunoscute este nenul, adica principal. Necunoscutele 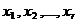 se numesc
principale. Trecem in membrul drept al ecuatiilor (5) toti termenii care
contin necunoscutele (secundare): se numesc
principale. Trecem in membrul drept al ecuatiilor (5) toti termenii care
contin necunoscutele (secundare):  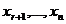 ; le atribuim valori arbitrare, respectiv ; le atribuim valori arbitrare, respectiv 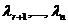 . Obtinem un sistem de r ecuatii cu r necunoscute: . Obtinem un sistem de r ecuatii cu r necunoscute: 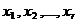 . .
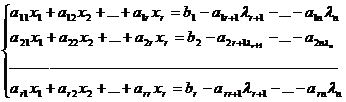 (6) (6)
Se rezolva acest sistem cu formulele lui Cramer; el are o
solutie unica 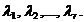 Numerele Numerele 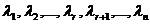 formeaza o solutie a
sistemului (5), care este si solutie a sistemului (1). Cum valorile formeaza o solutie a
sistemului (5), care este si solutie a sistemului (1). Cum valorile 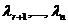 ale necunoscutelor
secundare ale necunoscutelor
secundare 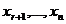 sunt alese arbitrar,
obtinem in acest mod o infinitate de solutii distincte ale sistemului (5),
care constituie multimea solutiilor sistemului (1). sunt alese arbitrar,
obtinem in acest mod o infinitate de solutii distincte ale sistemului (5),
care constituie multimea solutiilor sistemului (1).
Pe de alta parte, orice solutie a sistemului (5) poate fi
obtinuta prin acest procedeuIn concluzie, fiind dat un sistem de ecuatii
liniare (1) a carui rezolvare si cere, procedam in modul urmator:
Studiem daca sistemul
este compatibil. Pentru aceasta gasim un minor principal al matricei A a sistemului,
apoi calculam minorii caracteristici.
10 Daca exista
cel putin un minor caracteristic nenul, atunci sistemul este incompatibil.
20 Daca toti
minorii caracteristici sunt nuli, atunci sistemul este compatibil.
. Pentru gasirea solutiilor unui sistem compatibil (1),
procedam astfel:
Pastram din sistemul (1)
ecuatiile care corespund liniilor minorului principal. In aceste ecuatii,
trecem in membrul drept termenii care contin necunoscutele secundare, in
membrul stang pastrand numai termenii care contin necunoscutele principale.
Atribuim necunoscutelor secundare valori arbitrare, apoi calculam cu ajutorul
formulelor lui Cramer valorile necunoscutelor principale, obtinand astfel
toate solutiile sistemului (1).
Pentru
ca sistemul compatibil (1) sa aiba solutie unica este necesar si suficient
ca rangul matricei sistemului sa fie
egal cu numarul necunoscutelor.
Aplicatii.
.Sa se rezolve sistemul 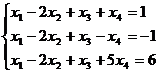
Rezolvare.
Sa scriem matricele:
A=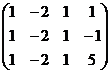 si si 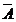 = = 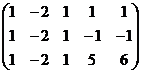 . .
Deoarece avem 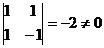 , iar , iar 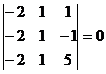 si si 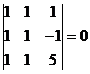 , rezulta ca rangul
matricei A este 2, iar minorul , rezulta ca rangul
matricei A este 2, iar minorul 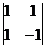 este principal. este principal.
Calculam minorii caracteristici. Avem doar un singur
minor caracteristic si anume:
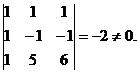
Deoarece acesta este nenul, sistemul este incompatibil.
. Sa se rezolve sistemul 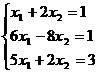
Rezolvare.
Matricea coeficientilor are rangul 2, un minor principal
al sau fiind, de exemplu: 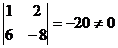
Exista un singur minor caracteristic si anume 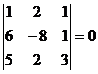 . .
Acesta fiind nul, sistemul este compatibil si are
solutie unica. Pentru gasirea solutiei, rezolvam sistemul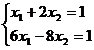 . .
Obtinem solutia: 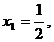 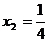 . Aceste valori satisfac si ecuatia a treia a sistemului
initial. . Aceste valori satisfac si ecuatia a treia a sistemului
initial.
. Sa se rezolve sistemul 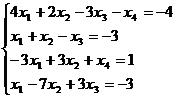 . .
Rezolvare.
Calculam determinantul sistemului si obtinem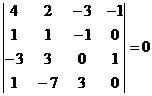
Cu toate ca numarul de ecuatii este egal cu numarul de
necunoscute, nu se pot folosi direct formulele lui Cramer, deoarece
determinantul sistemului este nul. Matricea coeficientilor este de rang 3 un minor
principal fiind, de exemplu 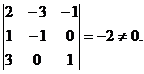
Exista un singur minor caracteristic :
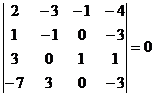
Care fiind nul sistemul este compatibil.
Consideram primele trei ecuatii cu necunoscutele
principale 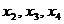 . Daca . Daca 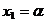 fiind necunoscuta secundara, gasim: fiind necunoscuta secundara, gasim: 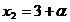 , , 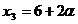 , , 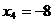 . .
Un sistem
de ecuatii liniare se numeste omogen daca termenul liber al
fiecarei ecuatii este nul ( adica fiecare ecuatie este omogena). Asadar,
forma generala a unui sistem omogen de ecuatii liniare este 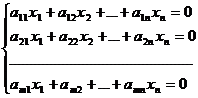 (1) (1)
In
legatura cu sistemele omogene, observam urmatoarele:
1. Un
sistem omogen este intotdeauna compatibil. Intr-adevar, termenii liberi fiind
nuli, rezulta ca adaugand la coloanele maricei sistemului coloana nula a
termenilor liberi rangul nu se
schimba. Deci, conform teoremei Kronecker-Capelli, sistemul este compatibil.
De
altfel, aceasta se vede direct, intrucat un astfel de sistem admite solutia nula: 0,0,,0.
Sa
presupunem ca matricea A a coeficientilor este de rang r.
- Daca r=n
( numarul necunoscutelor), atunci solutia nula este singura solutie
a sistemului (1).
- Daca r<n
( numarul necunoscutelor), atunci sistemul (1) are si solutii
nenule. Pentru a gasi solutiile, se utilizeaza acelasi procedeu ca in
cazul sistemelor arbitrare.
Observatii. 1). Un sistem de n ecuatii liniare omogene cu n necunoscute are solutii nenule daca si numai
daca determinantul sau este nul.
2). Daca un sistem de ecuatii liniare
omogene are numarul ecuatiilor mai mic decat cel al necunoscutelor, sistemul
are solutii nenule.
Aplicatii.
Sa se determine valorile
parametrului 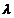 pentru care sistemul
de ecuatii are solutii nenule pentru care sistemul
de ecuatii are solutii nenule 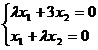
Rezolvare.
Determinantul
sistemului este 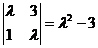 . Acesta este nul pentru . Acesta este nul pentru 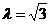 sau sau 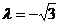 ; in aceste cazuri sistemul are solutii nenule. ; in aceste cazuri sistemul are solutii nenule.
Sa se rezolve sistemul
omogen 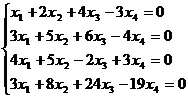 . .
Rezolvare.
Calculam
mai intai, determinantul sistemului, care este nul. Deoarece 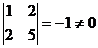 , si toti minorii de ordin trei care se obtin prin bordarea
acestuia cu una dintre coloanele si una dintre liniile ramase sunt nuli,
rezulta ca acesta este un minor principal. , si toti minorii de ordin trei care se obtin prin bordarea
acestuia cu una dintre coloanele si una dintre liniile ramase sunt nuli,
rezulta ca acesta este un minor principal.
Pentru
a obtine solutiile, dam necunoscutelor 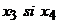 valori arbitrare valori arbitrare 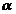 respectiv respectiv 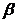 , si deducem valorile necunoscutelor , si deducem valorile necunoscutelor 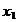 si si 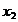 din sistemul: din sistemul:
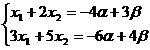
Rezulta 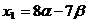 , , 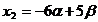 , , 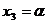 , , 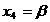 , , 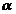 si si 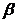 fiind numere
oarecare. fiind numere
oarecare.
|


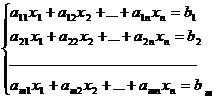 (1)
(1)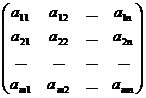
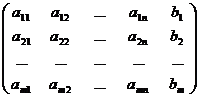
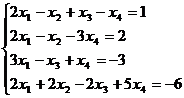
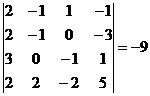
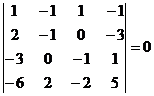 ,
,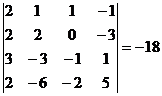
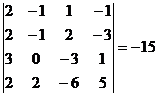 ,
,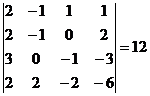
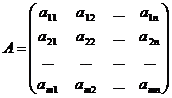 ,
, 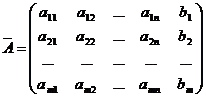 .
.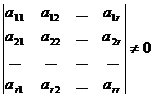 .
.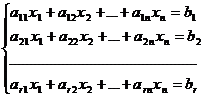
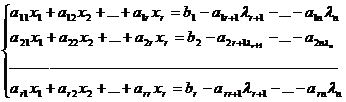
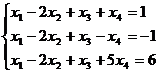
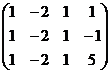
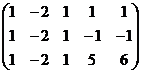 .
.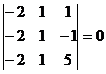 si
si 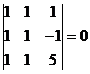 , rezulta ca rangul
matricei A este 2, iar minorul
, rezulta ca rangul
matricei A este 2, iar minorul 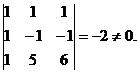
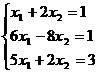
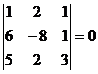 .
.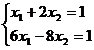 .
.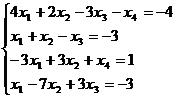 .
.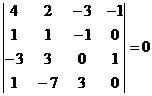
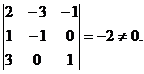
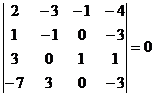
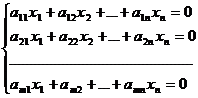 (1)
(1)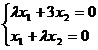
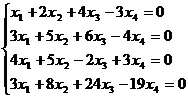 .
.