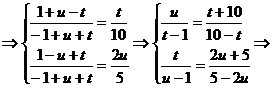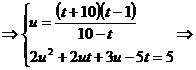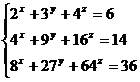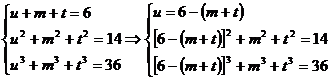Sisteme de ecuatii exponentiale si
logaritmice
Exemple
Sa se rezolve, in 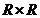 , sistemul
, sistemul

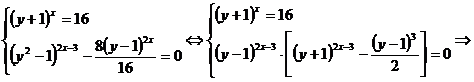
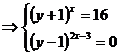 (1) sau
(1) sau 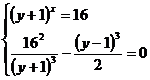 (2)
(2)
Din 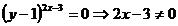 ,
, 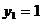 si atunci prima
ecuatie a sistemului (1)
si atunci prima
ecuatie a sistemului (1)
se scrie 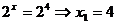
Din 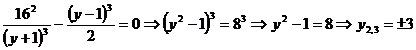
Pentru 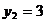 din prima ecuatie
a sistemului (2)
din prima ecuatie
a sistemului (2) 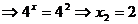 , iar pentru
, iar pentru
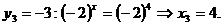 Deci solutiile sistemului sunt
Deci solutiile sistemului sunt
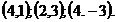

2)Sa se
rezolve, in 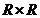 , sistemul
, sistemul
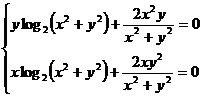
Dind factor comun pe 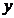 in prima ecuatie
si pe
in prima ecuatie
si pe 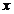 in ecuatia a
doua, sistemul este echivalent cu sistemele
in ecuatia a
doua, sistemul este echivalent cu sistemele
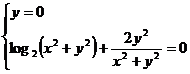 (1)
(1) 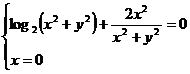 (2)
(2)
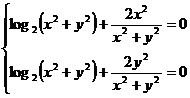 (3)
(3)
(cazul 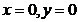 nu poate avea loc)
nu poate avea loc)
Din (1) se
obtine 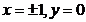 , din (2)
, din (2) 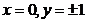 , iar din (3) sistemul echivalent
, iar din (3) sistemul echivalent
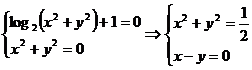 sau
sau 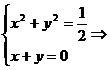
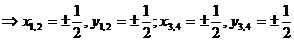
Solutiile
sistemului sunt:
3)Sa se resolve sistemul:
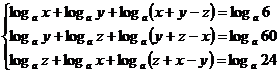 ;
; 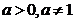
Din sistem
rezulta ca 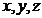 sunt numere reale strict
pozitive.Sistemul se scrie
sunt numere reale strict
pozitive.Sistemul se scrie
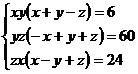
Notam 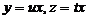 sistemul devine
sistemul devine
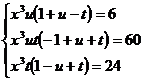 (1)
(1) 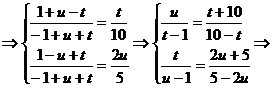
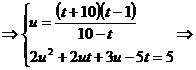
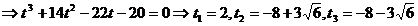
Deoarece 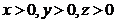 trebuie ca
trebuie ca 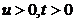 , astfel ca numai solutia
, astfel ca numai solutia
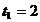 convine.Pentru
convine.Pentru 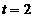 rezulta
rezulta 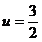 si din (1)
si din (1) 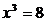 , adica
, adica 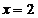 .
.
Celelalte necunoscute
sunt 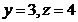
4)Sa se
rezolve, in 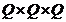 , sistemul
, sistemul
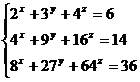
Notam 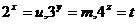 , sistemul se scrie
, sistemul se scrie
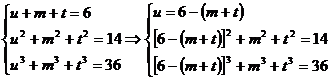
Notam 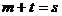 si se obtine
si se obtine
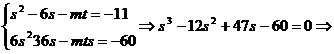
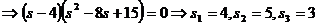
Pentru 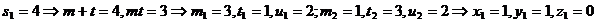
sau
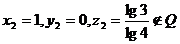
Pentru 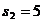 se obtine analog
se obtine analog 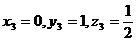 sau
sau 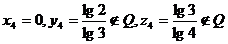
Pentru 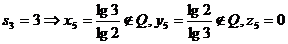 sau
sau 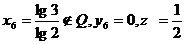
Solutiile
sistemului sunt: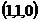 si
si 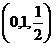



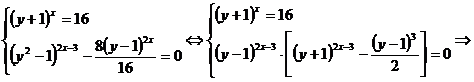
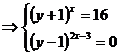
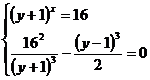 (2)
(2)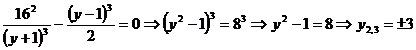
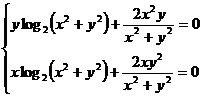
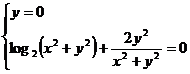
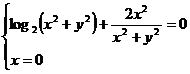 (2)
(2)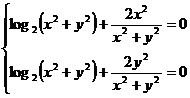 (3)
(3)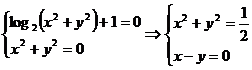 sau
sau 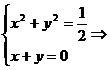
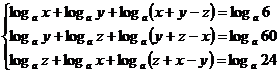 ;
; 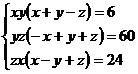
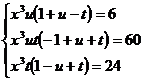 (1)
(1)