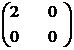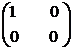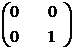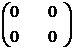INELE
Se
numeste inel o multime nevida A, impreuna cu doua
operatii algebrice, dintre care una se noteaza de regula aditiv,
iar cealalta multiplicativ, cu urmatoarele proprietati:
a) A impreuna
cu operatia aditiva este grup abelian;
b) A impreuna
cu operatia de inmultire este semigrup;
c) operatia
de inmultire este distributiva fata de adunare, deci:
a
(b+c) = ab + ac,
(b+c)
a = ba + ca
 pentru orice a, b,
c A.
pentru orice a, b,
c A.
Pe o multime formata
dintr-un singur element exista o singura structura de inel in
care acel element este elementul nul si elementul unitate. Acest inel va
fi numit inel nul. Un inel care contine cel putin doua elemente
va fi numit inel nenul.
Inelul A
- se numeste comutativ
daca operatia de inmultire este comutativa;
-
se numeste unitar sau inel cu element unitate daca operatia de
inmultire are element unitate, adica semigrupul multiplicativ este
unitar.
Daca 0 este elementul unitate
pentru operatia de adunare din A, atunci avem 0a = a0 =0, pentru orice a A. Intradevar avem a0 = a(0+0) = a0+a0 si deci, adunand la ambii membrii ai
acestei relatii pe -a0, obtinem a0 =0. Faptul ca 0a = 0 se
demonstreaza cu totul analog.
Un element a din
inelul A se numeste divizor al lui
zero la stanga ( la dreapta) daca
exista b ≠ 0, b A, astfel ca ba = 0 (respectiv ab = 0 ). Rezulta astfel
ca 0 este divizor al lui zero la stanga si la dreapta in orice inel
nenul. Un
inel nenul A comutativ,cu element unitate si care nu are divizori ai lui
zero se numeste inel integru sau domeniu de integritate. Spunem ca
inelul A nu are divizori ai lui zero daca 0 este singurul divizor al lui
zero in A si spunem ca A are divizori ai lui zero in caz contrar.
Daca a A si -a este opusul sau, atunci
pentru orice b,c A avem c(b-a) = cb - ca si (
b-a)c = bc - ac. In particular, (-a)b =
a(-b) = - (ab). Intradevar, fie b - a = d, atunci b = d + a si cb = cd + ca, adica cb - ca = cd = c(b-a). A doua relatie se
demonstreaza analog. Elementele inversabile pentru operatia de inmultire din
inelul (unitar) A se mai numesc si unitati ale lui A [ a se face distinctie intre o unitate a unui
inel (element inversabil) si elementul unitate al inelului]. Aceste elemente formeaza un grup multiplicativ.
Propozitia
I : Daca inelul unitar A este
diferit de inelul nul, atunci orice element inversabil din A nu este divizor al
lui zero, in particular este ≠ 0 si 1 ≠ 0.
Demonstratie : Sa
presupunem ca a este element inversabil in A si ca ar fi divizor al lui zero la
dreapta. Atunci ar exista b≠ 0
astfel ca ab = 0. Inmultind
aceasta relatie cu inversul lui a, care exista, obtinem b =
0, clara contradictie.
Definitie: Fiind date doua inele A,B, o
functie φ: A→B se numeste morfism (sau omomorfism) de
inele daca satisface urmatoarele doua proprietati:
1) φ(a + b) = φ(a) + φ(b), pentru orice a,b A;
2) φ(ab) =
φ(a) φ(b), pentru orice a,b A.
Prima proprietate exprima
faptul ca φ este, in particular, un morfismde grupuri de la grupul
aditiv al lui A la grupul aditiv al lui B. Deci din proprietatile morfismelor de grupuri rezulta
atunci ca φ(0) = 0 (am notat cu 0 elementul nul in A si B)
si φ(-a) = -φ(a), pentru orice a A.
Din a doua proprietate insa nu
se poate deduce ca φ(1) = 1 (cu 1 am notat elementul unitate la
inmultire din A si B) in cazul
in care A si B sunt inele unitare. Daca aceasta proprietate este
insa satisfacuta, se spune ca morfismul φ este
unitar. Se verifica
imediat ca compunerea (in sensul compunerii functiilor) a doua
morfisme (unitare) de inele este inca un morfism (unitar) de inele. De
asemenea, functia identica 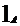 : A→A este
pentru orice inel A un morfism de inele (evident acest morfism este unitar
daca A are element unitate).
: A→A este
pentru orice inel A un morfism de inele (evident acest morfism este unitar
daca A are element unitate).
Daca A→B este un morfism unitar de inele, A fiind un inel comutativ, atunci se
spune ca B este o A-algebra, daca pentru orice a A, b B avem φ(a)b = bφ(a) (ultima
conditie este intotdeauna verificata daca B este comutativ). De obicei, atunci cand
nu se poate face nicio confuzie, pentru a A si b B produsul φ(a)b = bφ(a) se
noteaza cu ab = ba. Se
verifica imediat ca daca B este o A-algebra comutativa, iar C este
o B-algebra, atunci C este o A-algebra prin intermediul compunerii morfismelor
respective. Morfismul φ se numeste morfismul structural (sau de
structura) al A-algebrei B. Notiunea de A-algebra este mai des utilizata in cazul in
care A este corp comutativ. O A-algebra se numeste
comutativa daca B este inel comutativ. Deci, un acelasi inel B
poate sa aiba mai multe structuri de A-algebra.
Fie φ:
A→B si φ: A→C doua A-algebre. Atunci
o functie θ: B→C se
numeste
morfism
de A-algebre daca θ este un morfism
de inele si θφ =
ψ, adica diagrama 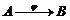
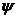
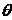

C este comutativa. Numim endomorfism al inelului A un morfism de inele de la A la A.
Un morfism de inele φ:
A→B se numeste injectiv
daca functia φ este injectiva. Morfismul
φ se numeste surjectiv daca φ este o functie surjectiva.
Spunem ca un morfism de inele
φ: A→B este izomorfism
daca exista un morfism de inele φ :B→A astfel incat
:B→A astfel incat  φ
φ φ =
φ = 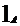 , φφ
, φφ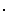 =
=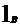 . Ca si la
grupuri si multimi este adevarata urmatoarea
propozitie: Propozitia
1.4: Un morfism de inele este
izomorfism daca si numai daca este bijectiv (adica este
injectiv si surjectiv).
. Ca si la
grupuri si multimi este adevarata urmatoarea
propozitie: Propozitia
1.4: Un morfism de inele este
izomorfism daca si numai daca este bijectiv (adica este
injectiv si surjectiv).
Demonstratie: Daca φ: A→B este izomorfism
de inele,atunci rezulta ca φ este si un izomorfism de
multimi (si de grupuri), deci dupa cum stim este bijectie.
Reciproc, daca φ este morfism bijectiv, atunci el este in particular
un izomorfism de grupuri, deci exista φ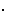 :B→A, morfism de grupuri, astfel ca φ
:B→A, morfism de grupuri, astfel ca φ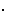 φ=
φ= 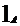 si φφ
si φφ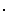 =
=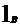 . Ramane
doar sa aratam ca φ
. Ramane
doar sa aratam ca φ este chiar morfism de inele, adica satisface
conditia 2) de mai sus. Fie
deci a `, b` B; trebuie sa aratam ca φ
este chiar morfism de inele, adica satisface
conditia 2) de mai sus. Fie
deci a `, b` B; trebuie sa aratam ca φ ( a ` b`) = φ
( a ` b`) = φ ( a `) φ
( a `) φ (b`). Avem φ(φ
(b`). Avem φ(φ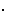 ( a ` b`)) = a ` b` si φ( φ
( a ` b`)) = a ` b` si φ( φ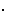 ( a `) φ
( a `) φ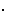 ( b`)) = φ(φ
( b`)) = φ(φ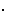 ( a)) φ(φ
( a)) φ(φ ( b)) = a ` b` si afirmatia rezulta din
faptul ca φ este functie injectiva.
( b)) = a ` b` si afirmatia rezulta din
faptul ca φ este functie injectiva.
Multimea numerelor intregi Z,
multimea numerelor rationale Q si multimea numerelor reale
R cu operatiile de adunare si inmultire formeaza inel.
Acestea sunt inele comutative cu element unitate, iar injectiile canonice
Z →Q→R sunt evident morfisme unitare de inele. Elementele
inversabile in Z sunt 1 si -1, iar in Q si R toate elementele nenule.
In inelul Z daca
consideram subgrupul nZ ale
grupului aditiv al lui Z, unde n Z,atunci este clar ca,
considerand pe acest subgrup si operatia de inmultire, avem pe nZ o structura de
inel comutativ care nu are element unitate daca n ≠ ±1 si n ≠ 0, adica nZ ≠ Z si nZ ≠ (0). Inelele
nZ pentru orice n Z, n >1, sunt evident fara divizori ai lui 0; injectiile canonice nZ→Z sunt morfisme
de inele.
n Z, n >1, sunt evident fara divizori ai lui 0; injectiile canonice nZ→Z sunt morfisme
de inele.
Fie A si B doua inele.
Atunci considerandu-le cu structura lor de grupuri abeliene, putem construi
produsul lor direct A  B, care este, de
asemenea,un grup abelian. Putem insa introduce pe A
B, care este, de
asemenea,un grup abelian. Putem insa introduce pe A  B o structura de inel dedusa din
structurile de inele ale lui A si B in modul urmator: definim pe
A
B o structura de inel dedusa din
structurile de inele ale lui A si B in modul urmator: definim pe
A  B
urmatoarea operatie de inmultire ( a , b) ( a `, b`) = (a a `,b
b`) pentru a, a ` A si b, b` B. Se verifica imediat ca,
cu aceste doua operatii algebrice, A
B
urmatoarea operatie de inmultire ( a , b) ( a `, b`) = (a a `,b
b`) pentru a, a ` A si b, b` B. Se verifica imediat ca,
cu aceste doua operatii algebrice, A  B formeaza inel (verificarea
distributivitatii inmultirii fata de adunare este
imediata,ea se face pe componente). Evident, daca A si B sunt inele comutative si produsul lor direct este un inel
comutativ, iar daca A si B sunt unitare si notam elementul
unitate ci 1 in ambele inele, atunci elementul (1,-1) este unitate in produsul
direct A × B. Daca inelele A si B sunt nenuleatunci produsul lor
direct A × B este un inel cu divizori ai lui zero. Intradevar,
daca a A, a ≠ 0, b B, b ≠ 0, atunci (a,0) (0,b) = (0,0). In particular,
inelul Z × Z are divizori ai lui zero.
B formeaza inel (verificarea
distributivitatii inmultirii fata de adunare este
imediata,ea se face pe componente). Evident, daca A si B sunt inele comutative si produsul lor direct este un inel
comutativ, iar daca A si B sunt unitare si notam elementul
unitate ci 1 in ambele inele, atunci elementul (1,-1) este unitate in produsul
direct A × B. Daca inelele A si B sunt nenuleatunci produsul lor
direct A × B este un inel cu divizori ai lui zero. Intradevar,
daca a A, a ≠ 0, b B, b ≠ 0, atunci (a,0) (0,b) = (0,0). In particular,
inelul Z × Z are divizori ai lui zero.
Aplicatiile canonice
i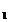 : A→ A × B, i
: A→ A × B, i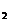 : B→ A× B
: B→ A× B
p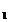 : A× B→
A, p
: A× B→
A, p : A×
B→B
: A×
B→B
definite
prin i (a) = (a,0), i
(a) = (a,0), i (b) = (0,b), p
(b) = (0,b), p (a,b) = a, p
(a,b) = a, p (a,b) = b pentru a A, b B sunt morfisme de inele, p
(a,b) = b pentru a A, b B sunt morfisme de inele, p si p
si p sunt morfisme surjective unitare daca inelele
A si B sunt inele unitare, pe cand i
sunt morfisme surjective unitare daca inelele
A si B sunt inele unitare, pe cand i , i
, i nu sunt morfisme unitare pentru A si B inele
unitare nenule, ele sunt insa injective.
nu sunt morfisme unitare pentru A si B inele
unitare nenule, ele sunt insa injective.
Fie
M o multime si R un inel. Pe
multimea R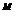 a functiilor de M la R se poate
introduce o structura de inel, indusa de structura de inel a lui R,
definind operatiile algebrice astfel:
a functiilor de M la R se poate
introduce o structura de inel, indusa de structura de inel a lui R,
definind operatiile algebrice astfel:
daca f, g R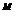
(f+g)(a)
= f(a) + g(a), pentru orice a R.
(fg)
(a) = f(a)g(a)
Este evident ca daca R este
inel comutativ, si inelul R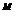 este comutativ.
este comutativ.
Aplicatia
canonica
φ:
R →R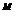 ,
,
definita
prin φ(a)(m) = a, pentru orice m M, a R, este un morfism injectiv de inele, care este
unitar daca R are element unitate si este izomorfism daca M este constituita dintr-un singur
element.
Daca , i I, este o familie de
inele, atunci putem defini pe produsul direct al grupurilor R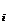 o structura de inel definind produsul pe componente; adica, pentru f, g R =
o structura de inel definind produsul pe componente; adica, pentru f, g R = 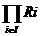
definim fg = h, unde h(i) = f(i) g(i), pentru
orice i I. Folosind
notatiile din aliniatul precedent, rezulta R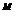 =
=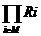 , unde R
, unde R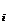 R.
R.
Fie
R un inel, M = , N = multimea primelor m, respectiv n numere naturale nenule. Consideram
multimea functiilor de la M×N cu valori in R, notata R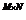 . Pe aceasta multime se poate introduce o
operatie algebrica indusa de operatia algebrica de
adunare a lui R, impreuna cu care aceasta multime formeaza
grup. Fie A R
. Pe aceasta multime se poate introduce o
operatie algebrica indusa de operatia algebrica de
adunare a lui R, impreuna cu care aceasta multime formeaza
grup. Fie A R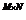 , atunci punand A(i,j) = a
, atunci punand A(i,j) = a R, i M, j N putem sa notam
pe A ca un tablou de forma
R, i M, j N putem sa notam
pe A ca un tablou de forma
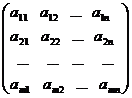
care
se numeste de obicei matrice cu elemente din inelul R, mai precis, matrice
cu m linii si n coloane cu elemente din inelul R. Importanta faptului ca se
considera matrice cu elemente dintr-un inel consta in aceea ca
intre anumite matrice se poate da o
compunere numita produsul matricelor. Anume, daca A 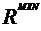 si B
si B 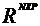 unde P = atunci cuplului A, B i se ataseaza o matrice C
unde P = atunci cuplului A, B i se ataseaza o matrice C 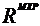 astfel: fie
astfel: fie
A
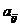
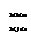
 , B = (
, B = (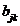
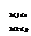 atunci C =
atunci C = 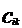
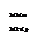
are
elementele definite astfel: 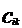
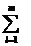 aijbjk. Asadar, pentru a obtine elementul
aijbjk. Asadar, pentru a obtine elementul
din
matricea C de pe linia i si coloana k se face suma produselor elementelor
corespunzatoare de pe linia i a matricei A cu cele de pe coloana j a matricei B. De aceea se spune uneori ca se "inmultesc
liniile cu coloanele" .
Se scrie C = AB.
Compunerea matricelor nu este o
operatie algebrica definita pe multimea tuturor
matricelor; ea este asemanatoare compunerii functiilor,
compunerii morfismelor de grupuri sau inele etc. Vom vedea ulterior
legatura strinsa care exista intre inmultirea matricelor
si morfismele de module.
Vom nota cu Mmxn(R) multimea tuturor
matricelor cu m linii si n coloane cu elemente din inelul R si vom considera pe aceasta
multime operatia dedusa din operatia de adunare pe R cu care formeaza grup comutativ (notat
aditiv).
Inmultirea matricelor are
urmatoarele proprietati: a) Daca A 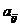
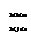
 B
= (
B
= (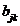
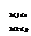 , C
, C 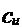
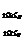
atunci
(AB)C = A(BC),
deci
o proprietate de asociativitate. Se observa mai intii ca in (1)
produsele sunt definite. Sa
demonstram acum egalitatea (1). Fie
AB = (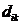
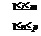 atunci
atunci 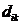 =
= 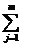
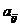
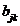 si (AB)C =
si (AB)C = 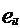 )
)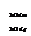
unde
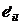
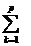
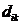
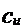
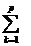
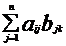
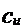
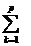
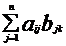
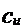
Fie:
BC = (
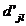
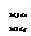 atunci
atunci 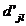 =
=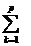
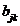
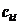 si
daca A BC) = (
si
daca A BC) = (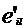 atunci
atunci
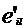
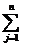
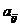
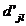
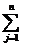
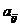
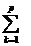
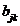
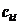
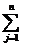
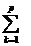
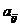
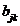
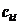 ceea ce demonstreaza
egalitatea (1). b) Daca A = (
ceea ce demonstreaza
egalitatea (1). b) Daca A = (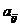 )
)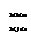 B = (
B = (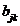 )
)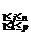 , C = (
, C = (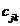
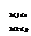
atunci A(B + C) = AB
+ AC.
In adevar, daca
A(B + C) = (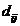
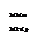 atunci
atunci 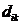 =
=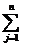
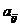
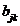
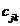
Daca AB + AC = (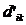 ), atunci
), atunci 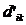 =
=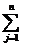
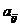
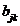
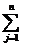
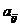
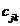
si
egalitatea ceruta rezulta din distributivitatea inmultirii
fata de adunare in inelul R.
Analog,
daca
A= 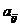
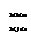 B =
B = 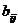 )
)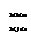 , C =
, C = 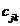
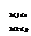
atunci
(A + B)C = AC + BC.
Este
evident, de asemenea, ca daca A este matricea din Mmxn(R) cu toate elementele nule (deci
elementul nul al grupului aditiv), atunci pentru orice matrice B Mnxp(R) avem AB = A0 . Daca B este elementul nul al .grupului Mnxp(R) iar A o matrice oarecare din Mmxn(R) atunci AB
= A0, unde A0 este elementul nul al
grupului Mmx p(R).
Daca se considera grupul
matricelor Mmxm(R) pe care il vom nota cu Mm(R), atunci operatia de compunere definita
mai sus induce pe Mm(R) o operatie algebrica notata
multiplicativ si Mm(R) impreuna cu
operatia de adunare si inmultire astfel definita
formeaza un inel, numit inelul matricelor patrate de ordinul m.
Acest lucru rezulta imediat din proprietatile produsului de
matrice, demonstrate mai sus. Daca inelul A are element unitate, atunci matricea
E = (δ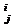 Mm(R),cu
Mm(R),cu 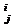
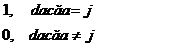
este
element unitate in acest inel, dupa cum se verifica cu
usurinta (functia δ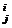 definita mai sus se
numeste simbolul lui Kronecker, uneori se scrie
definita mai sus se
numeste simbolul lui Kronecker, uneori se scrie  Matricea E are forma
Matricea E are forma
E =  Inelul
Inelul 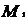 (R) este evident izomorf cu R prin morfismul
care asociaza elementului a R matricea cu o singura
linie si coloana
(a). Daca R este inel cu element unitate diferit de 0, atunci
inelul Mm(R) nu este comutativ pentru m > 0. Vom demonstra acest lucru pentru m = 2, pentru m > 2 demonstratia se face analog. Fie A =
(R) este evident izomorf cu R prin morfismul
care asociaza elementului a R matricea cu o singura
linie si coloana
(a). Daca R este inel cu element unitate diferit de 0, atunci
inelul Mm(R) nu este comutativ pentru m > 0. Vom demonstra acest lucru pentru m = 2, pentru m > 2 demonstratia se face analog. Fie A = 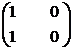 si B
si B 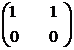 atunci AB =
atunci AB =  si BA =
si BA =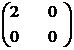
deci AB 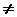 BA.
BA.
In aceleasi conditii Mm (R) are divizori ai lui zero. Vom arata acest lucru pentru matricele de ordinul 2. Se
observa ca:
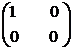
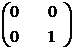
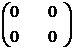
Functia φ: R →Mm(R),
definita prin φ(a) 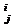 a) este un morfism
unitar de inele. In adevar, este clar ca φ pastreaza sumele si duce elementul unitate in
elementul unitate. Sa
aratam ca pastreaza si produsele. Fie a,b R, atunci φ (ab)
a) este un morfism
unitar de inele. In adevar, este clar ca φ pastreaza sumele si duce elementul unitate in
elementul unitate. Sa
aratam ca pastreaza si produsele. Fie a,b R, atunci φ (ab) 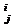 ab) iar φ(a) φ(b) =(cij unde cij =
ab) iar φ(a) φ(b) =(cij unde cij =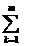
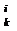 a)
a) 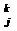 b)=
b)= 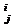 ab) . De asemenea se
verifica imediat ca, daca R este inel
comutativ, φ(a)A = A φ(a), unde a R , A Mm(R) si deci in acest
caz Mm(R) are o structura de R- algebra.
ab) . De asemenea se
verifica imediat ca, daca R este inel
comutativ, φ(a)A = A φ(a), unde a R , A Mm(R) si deci in acest
caz Mm(R) are o structura de R- algebra.
Pentru a R si A =
(aij ) o matrice din Mm(R), avem ca φ(a)A = (aaij ) si
se noteaza aceasta matrice cu aA. Analog, Rφ(a) se noteaza cu Aa. Aceasta conventie de notatie se
obisnuieste intotdeauna
pentru un
morfism de inele si generalizeaza conventia facuta
pentru R-algebre, R fiind in acel caz inel comutativ. Orice inel R cu element
unitate are o unica structura de Z-algebra,
adica
exista
un
singur morfism unitar de inele φ:
Z→R. In adevar, daca φ
atunci in mod necesar φ(n) = 1+ + 1 = n · 1 (de n ori) pentru n > 0 si φ(n) = - (1+ .. +1) = n · 1 (de -n ori) pentru n< 0 si astfel φ este complet
definita si se observa ca este morfism de inele
(adica pastreaza si produsele).
Fie R un inel care nu are element unitate. Atunci lui ii
putem asocia un inel unitar
in modul urmator: consideram produsul direct al grupurilor aditive Z
X R pe care introducem urmatoarea
operatie de inmultire:
(n, a)(n', a') = (nn', na' + an' + aa').
Se verifica imediat ca
aceasta inmultire este asociativa si distributiva
fata de adunare. Deci Z x R formeaza un inel. Acest inel are ca element
unitate elementul (1,0) si daca R este
comutativ inelul Z xR este
comutativ. Functia φ:
R→ Z X R, definita prin φ(a) = (0, a), este evident un morfism de inele, deci A se poate identifica cu un subinel al lui ZxR.
Folosind
proprietatile de mai sus, se poate constata ca multe
proprietati ale inelului R se pot
obtine din proprietati corespunzatoare ale inelului cu element
unitate ZxR
asociat lui R.


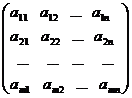

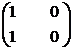 si
si 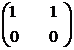
 si BA =
si BA =