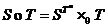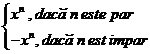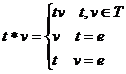Grupuri
si inele
Definitie 1. O multime G inzestrata cu o lege de compozitie interna f, se numeste grup daca legea f
indeplineste urmatoarele conditii, numite axiomele grupului :
(G1) 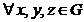 , f(f(x, y), z) =
f(x, f(y, z); (legea este asociativa)
, f(f(x, y), z) =
f(x, f(y, z); (legea este asociativa)
(G2) 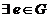 , astfel incat
, astfel incat 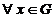 , f(x, e) = f(e, x) = x; (legea poseda element
neutru)
, f(x, e) = f(e, x) = x; (legea poseda element
neutru)
(G3) 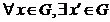 , astfel incat f(x, x')
= f(x', x) = e; (orice element din G
este simetrizabil).
, astfel incat f(x, x')
= f(x', x) = e; (orice element din G
este simetrizabil).
Daca legea este
comutativa atunci grupul se numeste comutativ (abelian).
Definitia 2. O multime G inzestrata cu o lege de
compozitie interna * asociativa, se numeste grup daca 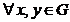 , ecuatiile a * x = b, y * a = b au solutii (unice)
in G.
, ecuatiile a * x = b, y * a = b au solutii (unice)
in G.
Observatie 3. Un semigrup este grup, daca si
numai daca ecuatiile a * x = b,
y * a = b au solutii (unice) in G,
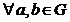 .
.
Definitie O multime G inzestrata cu o lege de compozitie interna *
asociativa, se numeste grup daca
legea * poseda element unitate la
stanga si 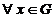 poseda
element simetric la stanga.
poseda
element simetric la stanga.
Observatie 5. In definitia 1. axiomele (G2), (G3) pot
fi inlocuite respctiv cu
(G2') 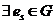 , astfel incat
, astfel incat 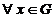 , f(es, x) =
x; (legea poseda element neutru la stanga)
, f(es, x) =
x; (legea poseda element neutru la stanga)
(G3') 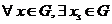 astfel incat f(xs,
x) = es; (orice element x poseda simetric la stanga)
astfel incat f(xs,
x) = es; (orice element x poseda simetric la stanga)
Un grup G se numeste grup finit daca multimea G este finita si infinit
in caz contrar.
Daca G este un grup, se numeste ordinul grupului G cardinalul lui G notat |G|; daca G este
finit, |G| este numarul natural
egal cu numarul elementelor lui G.
Propozitie 6. Fie G
un grup multiplicativ si x G. Atunci
G. Atunci 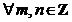 avem :
avem :
xnxm = xn + m;
(xn)m = xnm.
Definitie 7. Fie (G,*)
si (G', ◦) grupuri. O
aplicatie f : G → G' se
numeste omomorfism de grupuri
(sau morfism) daca
indeplineste conditia :
f(x * y) = f(x) ◦ f(y), 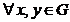
Un omomorfism de
grupuri f : G → G se
numeste endomorfism al grupului G.
Propozitie 8. Fie (G,*)
si (G', ◦) grupuri.
Daca f : G → G' este un omomorfism de grupuri, atunci f(e) = e', e si e' fiind
elementul unitate in G, respective G'.
Demonstratie :
Din relatiile x * e = e * x = x, 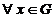 si f omomorfism avem
si f omomorfism avem
f(x, e) = f(x) ◦ f(e) = f(x) si f(e * x) = f(e) ◦ f(x)
= f(x)
Elementul unitate e' fiind unic, din f(x) ◦ f(e) = f(e) ◦ f(x) = f(x), rezulta f(e) = e'.
Propozitie 9. Imaginea simtricului unui element printr-un
morfism de grupuri este simetricul imaginii acelui element.
Demonstratie :
Fie f : G → G' un morfism de grupuri. Grupurile G si G' le presupunem fiind simplificarea scrierii multiplicative.
Avem 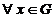 f(xx-1) =
f(x) f(x-1) = f(e) = e' si f(x-1x) = f(x-1)
f(x) = f(e) = e'.
f(xx-1) =
f(x) f(x-1) = f(e) = e' si f(x-1x) = f(x-1)
f(x) = f(e) = e'.
Din f(x) f(x-1) = f(x-1)
f(x) = e' rezulta ca f(x-1)
= [f(x)]-1.
Propozitie 10. Daca
f : G → G' si g : G' → G' sunt morfisme de grupuri, atunci g ◦ f este morfism de grupuri.
Demonstratie : Presupunem grupurile notate multiplicative. Avem 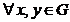
(g ◦ f)(xy) = g(f(xy)) = g[f(x)
f(y)] = g[f(x)] g[f(y)]= (g ◦ f)(x) (g ◦ f)(y).
Definitie 11. Un morfism de grupuri f : G → G' se numeste izomorfism de grupuri daca
exista un morfism de grupuri g : G' → G astfel
incat g ◦ f = 1G si
f ◦ g = 1G'.
Un morfism de grupuri este izomorfism daca si numai daca
este bijectiv.
Un izomorfism de grupuri f : G
→ G se numeste automorfism
al lui G.
Definitie 12. Fie G un grup. O
submultime nevida H a lui G se numeste subgrup al grupului G
daca legea de compozitie din G
induce pe H o lege de compozitie
impreuna cu care H este grup.
Teorema 13. O submultime nevida H
a unui grup (multiplicativ) G este
subgrup al grupului G daca
si numai daca sunt indeplinite conditiile :
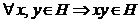 ,
,
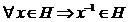 .
.
Demonstratie :
'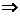 ' Presupunem H
subgroup al lui G. Din definitie
rezulta ca legea de compozitie din G induc o lege de compozitie pe H, adica are loc 1).
' Presupunem H
subgroup al lui G. Din definitie
rezulta ca legea de compozitie din G induc o lege de compozitie pe H, adica are loc 1).
Legea indusa poseda elemnt neutru e H astfel incat
H astfel incat 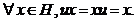 In particular uu = u si cum u este unic u = uu-1
= e; deci H contine
elemental neutru din G.
In particular uu = u si cum u este unic u = uu-1
= e; deci H contine
elemental neutru din G.
Deoarece H este subgrup orice
element x H este inversabil si inversul lui x in H
coincide cu inversul lui x in G, deoarce inversul este unic,
adica
H este inversabil si inversul lui x in H
coincide cu inversul lui x in G, deoarce inversul este unic,
adica 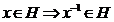 .
.
'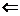 ' Presupunm 1) si 2) indeplinite. Din 1)
rezulta ca legea lui G induce
o lege pe H care este
asociativa. Din 2) rezulta ca pentru fiecare x
' Presupunm 1) si 2) indeplinite. Din 1)
rezulta ca legea lui G induce
o lege pe H care este
asociativa. Din 2) rezulta ca pentru fiecare x H avem x-1
H avem x-1 H si deci xx-1
= e
H si deci xx-1
= e H.
H.
Deci H impreuna cu legea
indusa este grup,adica subgroup a lui G.
Teorema 1 Orice submultime nevida H
a unui grup (multiplicativ) G este
subgrup al grupului G daca
si numai daca este indeplinita conditia : 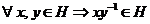 .
.
Fie G un grup si e G elmentul neutru. Submultimile G si al lui G
sunt subgrupuri, numite subgrupuri
improprii. Orice subgroup H a lui
G, diferit de G si se numeste subgrup
propriu.
G elmentul neutru. Submultimile G si al lui G
sunt subgrupuri, numite subgrupuri
improprii. Orice subgroup H a lui
G, diferit de G si se numeste subgrup
propriu.
Propozitie 15. Fie G un grup si (Hi)i I o familie de subgrupuri ale grupului G. Atunci intersectia H =
I o familie de subgrupuri ale grupului G. Atunci intersectia H = 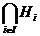 este tot un
subgrup al lui G.
este tot un
subgrup al lui G.
Definitie 16. Fie G un grup si X o submultime nevida a lui G. Se numeste subgrup a lui G genetat de X, intersctia toturor subgrupurilor
lui G care contin pe X. Multimea X se numeste sistem de
generatori al acestui subgrup notat
< X >.
Definitie 17. Un grup G se numste de tip finit sau finit generat,
daca exista o multime finita de elemente din G care genereaza pe G. Un grup generat de un singur element
se numeste grup ciclic sau monogen.
Definitie 18. Fie G un grup. Un subgrup H a lui G se numeste subgrup
invariant (sau divisor normal)
daca 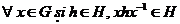 .
.
Conditia din definitie se mai scrie sub forma : 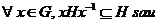 x(H)
x(H)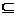 H,
unde x este
automorfismul interior al lui G
corespunzator elementului x.
Deci un subgroup este invariant, daca el contine odata cu orice
element al sau si transformatul acestuia prin orice automorfism
interior al lui G.
H,
unde x este
automorfismul interior al lui G
corespunzator elementului x.
Deci un subgroup este invariant, daca el contine odata cu orice
element al sau si transformatul acestuia prin orice automorfism
interior al lui G.
Definitie 19. Fie G un grup. Un subgrup H a lui G se numeste subgrup
invariant daca 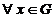 , xHx-1 = H.
, xHx-1 = H.
In orice grup G subgrupurile
improprii sunt subgrupuri invariante.
Teorema I Fie f : G → G' un
morfism de grupuri. Atunci exista un morfism injectiv de grupuri h : G / Ker f → G' astfel incat f = h ◦ p, unde p este morfismul canonic.
Demonstratie :
Fie 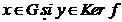 . Atunci f(xy) = f(x)
. Atunci f(xy) = f(x) G'. Deci exista o functie h : G / Ker f → G' definita prin h(x Ker f) = f(x).
G'. Deci exista o functie h : G / Ker f → G' definita prin h(x Ker f) = f(x).
Sa aratam ca h
este morfism.
Fie x Ker f, y Ker f  G / ker f. Atunci h(x
Ker f · y Ker f) = h(xy Ker f) = f(xy) =
G / ker f. Atunci h(x
Ker f · y Ker f) = h(xy Ker f) = f(xy) =
= f(x) f(y) = h(x Ker f) h(y Ker f).
Daca h(x Ker f) = h(y Ker f),
atunci f(x) = f(y) 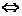 xy-1
xy-1 Ker f sau x
Ker f sau x y Ker f
y Ker f 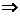
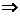 x Ker f = y Ker f. Dci morfismul h este injectiv.
x Ker f = y Ker f. Dci morfismul h este injectiv.
Fie x G. Atunci avem (h ◦ p)(x) = h[p(x)] = h(x Ker f) =
f(x).
G. Atunci avem (h ◦ p)(x) = h[p(x)] = h(x Ker f) =
f(x).
Deci, h ◦ p = f, adica
urmatoarea diagrama

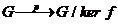


G'
este comutativa.
Teorema II Fie G un grup si H1 si H2 doua subgrupuri ale
grupului G astfel incat H1 sa fie subgrup
invariant al grupului generat in G de H1
si H2. Atunci H1 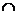 H2 este
subgrup invariant al grupului H2
si xista un izomorfism
H2 este
subgrup invariant al grupului H2
si xista un izomorfism
h : H2
/ H1 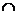 H2 →
/ H1.
H2 →
/ H1.
Demonstratie :
H2 fiind subgrup al grupului , fie H2 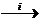
 / H1.
/ H1.
i este injectia canonica, iar p este surjectia canonica
si p ◦ i = φ.
Subgrupul
contine si pe H1
si pe H2, deci
contine si pe H1H2.
La fel H1H2 contine
si pe H1 si pe H2.
Fie xy H1H2 si zw
H1H2 si zw H1H2, unde x, z
H1H2, unde x, z  H1 si y, w
H1 si y, w H2. Atunci din egalitatea
H2. Atunci din egalitatea
yw-1H1 = H1yw-1 (pentru ca H1 este subgrup invariant in )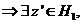 astfel ca (xy)(zw)-1
= x(yw-1z-1) = x(z'yw-1)
astfel ca (xy)(zw)-1
= x(yw-1z-1) = x(z'yw-1) H1H2. Deci H1H2 este subgrup in G care contine si pe H1
si pe H2. Prin
urmare, H1H2 contine
subgrupul .
Deci =
H1H2.
H1H2. Deci H1H2 este subgrup in G care contine si pe H1
si pe H2. Prin
urmare, H1H2 contine
subgrupul .
Deci =
H1H2.
Morfismul este injectiv.daca  H1H2, x
H1H2, x H1, y
H1, y H2 astfel ca p(xy) = p(x)p(y) =
p(y) = deoarece H1 este nucleul lui p. Atunci, (y) = (pi)(y) = p[i(y)] = p(y) =
H2 astfel ca p(xy) = p(x)p(y) =
p(y) = deoarece H1 este nucleul lui p. Atunci, (y) = (pi)(y) = p[i(y)] = p(y) =
Deci 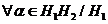 ,
, 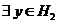 astfel incat (y) =
astfel incat (y) =
Teorema III Fie G
un grup si K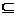 H doua subgrupuri invariante ale lui G. Atunci K este subgrup invariant al lui H,
H / K al lui G / K si
avem
H doua subgrupuri invariante ale lui G. Atunci K este subgrup invariant al lui H,
H / K al lui G / K si
avem 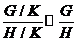 .
.
Demonstratie :
K fiind subgrup invariant in G avem K = xKx-1,
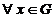 , in particular si pentru
, in particular si pentru 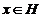 . Deci K este
subgrup invariant in H. Atunci, putem
considera grupurile factor respective,
. Deci K este
subgrup invariant in H. Atunci, putem
considera grupurile factor respective,
G / K, H / K si G / H. Consideram aplicatia f : G / K → G / H, f(xK) = xH. Acasta
aplicatie este un morfism surjectiv de grupuri. 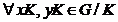 , f(xK · yK) = f(xyK) = = xyH = xH · yH = f(xK) · f(yK).
, f(xK · yK) = f(xyK) = = xyH = xH · yH = f(xK) · f(yK).
Morfismul f este surjectiv, deoarece pentru orice clasa xH G / H exista clasa xK
G / H exista clasa xK G / K astfel incat f(xK)
= xH.
G / K astfel incat f(xK)
= xH.
Aplicand teorema I rezulta ca exista un izomorfism h : (G / K) / ker f → G / H; ker f este subgrup
invariant in G / K si este
format din acele clase xK, astfel
incat f(xK) = 1 (unitatea lui G / H). Dar f(xK) = 1 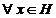 . Rezulta ker f =
= H / K.
. Rezulta ker f =
= H / K.
Deci exista izomorfismul 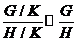 .
.
Inele
Definitie 20. O multime A inzestrata cu doua legi de compozitie interne,
notate de obicei una aditiv, iar cealalta multiplicativ, se numeste inel, daca sunt indeplinite
urmatoarel conditii :
(A1) A
impreuna cu operatia de adunare este grup ablian,
(A2) A
impreuna cu operatia de inmultire este semigrup,
(A3) Inmultirea
este distributiva bilateral fata de adunare, adica x(y + z) = xy + xz,
(y + z)x = yx + zx, 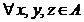 .
.
Daca
inmultirea in A este
comutativa inelul A se
numeste inel comutativ.
Daca exista
in A element neutru fata de
inmultire, atunci inelul A se
numeste inel cu element unitate sau
inel unitar.
Pe o multime
formata dintr-un singur element exista o singura structura
de inel, in care acel element este elementul nul. Acest inel il vom numi inel nul. Orice inel care contine
cel putin doua elemente il vom numi inel nenul.
Propozitie 21. Daca A
este inel si 0 A este elementul nul fata de adunare, atunci
A este elementul nul fata de adunare, atunci
x0
= 0x = 0, 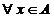 .
.
Propozitie 22. Daca A
este un inel si x, y A, atunci au loc relatiile :
A, atunci au loc relatiile :
(-x) y = x (-y) = - (xy),
(-x) (-y) = xy,
(-x)n = 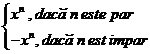
unde -x este opusul lui x A.
A.
Definitie 23. Fie A
un inel. Un element x A se numeste divizor
la stanga (la dreapta) al lui zero daca
A se numeste divizor
la stanga (la dreapta) al lui zero daca 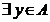 , y ≠
0 astfel incat xy = 0 (respectiv yx = 0).
, y ≠
0 astfel incat xy = 0 (respectiv yx = 0).
Definitie 2 Un inel nenul A, comutativ, cu element unitate si fara divizori ai lui
zero se numeste inel integru sau
domeniu de integritate.
Definitie 26. Fie A
si B doua inele. O
aplicatie f : A → B se
numeste omomorfism (sau morfism) de inele daca satisface urmatoarele doua
conditii :
f(x + y) = f(x) + f(y), 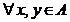 ;
;
f(xy) = f(x) · f(y), 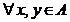 .
.
Definitie 27. Un morfism de inele f : A → B se numeste izomorfism de inele daca exista un morfism de inele g : B → A astfel incat g ◦ f = 1A si f
◦ g = 1B.
Daca exista un izomorfism de inele f : A → B atunci vom spune ca cele doua inele sunt
izomorfe si vom scrie A 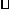 B.
B.
Teorema 28. Un morfism de inele este izomorfism de inele
daca si numai daca este bijectiv.
Definitie 29. O submultime A' a unui inel A se
numeste subinel al inelului A, daca legile de compozitie
interna din A induc legi de
compozitie interna pe A'
impreuna cu care A'
formeaza un inel.
Teorema 30. Fie A
un inel si A' o submultime
nevida a lui A. Atunci A' este subinel al inelului A daca si numai daca sunt
indeplinite urmatoarele conditii :
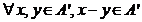
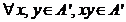 .
.
Propozitia 31. Intersectia unei familii de subinele ale
unui inel este un subinel.
Definitie 32. Fie A
un inel. O submultime nevida I
a lui A se numeste ideal stang (respectiv drept) sau ideal
la stanga (respctiv la dreapta) daca :
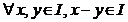
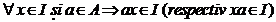 .
.
Un ideal I se numste bilateral daca este ideal la stanga si la dreapta.
Daca inelul A este comutativ notiunile de ideal
stang, ideal drept si ideal bilateral coincid.
Definitie 33. Fie A
un inel comutativ si I un ideal
al lui A. Multimea tuturor
elementelor x din A pentru care exista un intreg m > 0 astfel incat xm I este un ideal al lui A care se numeste radicalul
idealului I si se noteaza cu Rad
I sau
I este un ideal al lui A care se numeste radicalul
idealului I si se noteaza cu Rad
I sau 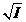 .
.
Teorema I Fie f :
A B un morfism de inele. Atunci exista un izomorfism canonic
: A / ker f → Im f, (x + ker f) = f(x).
Torema II Fie A
un inel, B un subinel a lui A si I un ideal in A. Atunci
exista un izomorfism de inele : B / (A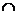 B) → (B + I) / I.
B) → (B + I) / I.
Torema III Fie A
un inel si I, J ideale
bilaterale in A, I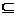 J. Atunci exista un izomorfism canonic de inele : A / J → (A / I) / (J / I).
J. Atunci exista un izomorfism canonic de inele : A / J → (A / I) / (J / I).
Produsul direct
Fie 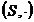 ,
, 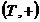 doua semigrupuri
si sa consideram produsul cartezian
doua semigrupuri
si sa consideram produsul cartezian 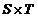 . Putem defini pe
. Putem defini pe 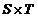 operatia
operatia 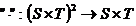 , definita astfel:
, definita astfel: 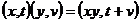 . Se observa usor ca
. Se observa usor ca 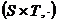 este un semigrup, el
fiind numit produsul direct al lui S cu T.
este un semigrup, el
fiind numit produsul direct al lui S cu T.
Avem asociate cu
produsul direct doua morfisme surjective de semigrupuri 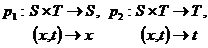 numite proiectii canonice. Impreuna
cu produsul direct, ele satisfac asa - numita "proprietate de universalitate a produsului direct":
numite proiectii canonice. Impreuna
cu produsul direct, ele satisfac asa - numita "proprietate de universalitate a produsului direct":
Teorema 3.21. 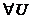 un semigrup si
un semigrup si 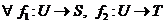 morfisme de
semigrupuri,
morfisme de
semigrupuri, 
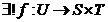 morfism astfel incat
morfism astfel incat 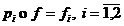 .
.
Demonstratie :
Fie 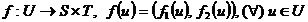 . Se constata usor ca f este un morfism de semigrupuri si
. Se constata usor ca f este un morfism de semigrupuri si 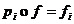 .
.
Sa
demonstram unicitatea: Fie 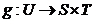 astfel incat
astfel incat 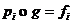 . Pentru orice
. Pentru orice 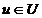 avem:
avem: 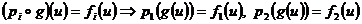 . Rezulta de aici ca
. Rezulta de aici ca 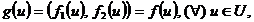 deci f este unica.
deci f este unica.
Produsul semidirect
Fie S, T
semigrupuri si sa presupunem ca avem un morfism de semigrupuri 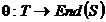 . Pe produsul cartezian
. Pe produsul cartezian 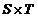 definim o noua
operatie:
definim o noua
operatie:
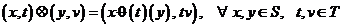 .
.
Se constata
usor ca 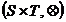 este un semigrup, el
fiind numit produsul semidirect al
lui S si T. Il vom nota
este un semigrup, el
fiind numit produsul semidirect al
lui S si T. Il vom nota 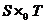 .
.
Produsul nodal (wreath product)
Notiunea de
"wreath product" este greu de tradus in limba romana. Din punct de vedere
a traducerii cuvant cu cuvant, "wreath" ar insemna "cununa". Denumirea de produs nodal a fost intrebuintata
de autorii primei carti de introducere algebrica in
informatica
Fie T semigrup. Lui ii putem asocia un
monoid 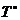 in modul urmator:
in modul urmator:
Daca T este monoid, 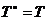 . In caz contrar, se considera un element
. In caz contrar, se considera un element 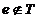 si definim pe
si definim pe 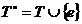 operatia
operatia 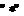 astfel:
astfel:
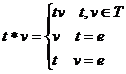
Este clar ca 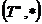 este monoid.
este monoid.
Fie S, T
doua semigrupuri, 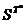 multimea tuturor
functiilor de la
multimea tuturor
functiilor de la 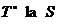 . Pe
. Pe 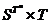 definim operatia:
definim operatia: 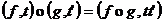 ,unde
,unde 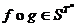 este definita prin
este definita prin 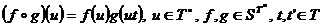
Sa
verificam asociativitatea. Fie 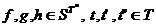 oarecare.
oarecare.
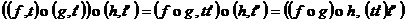
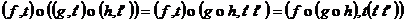
Pentru 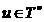 avem:
avem: 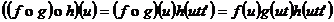 iar
iar 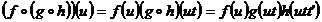 , ceea ce ne completeaza demonstratia.
, ceea ce ne completeaza demonstratia.
Asadar, 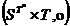 este semigrup si
va fi numit produsul nodal al lui S cu T.
este semigrup si
va fi numit produsul nodal al lui S cu T.
Intre produsul nodal
si produsul semidirect exista o stransa legatura:
Teorema 3.26. Daca S
si T sunt semigrupuri, atunci
exista 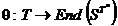 astfel incat
astfel incat