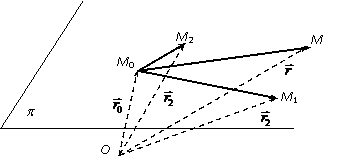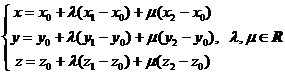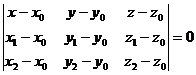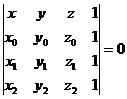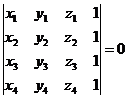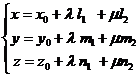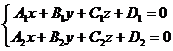|
Planul in spatiu
In spatiul
geometriei euclidiene E3,
un plan este in mod unic determinat de urmatoarele conditii:
1) trei puncte
necoliniare
2) un punct si
doua drepte neparalele
3) un punct si o
dreapta perpendiculara pe plan.
1.1.
Planul prin trei puncte
Fie M0, M1,
M2 I E trei puncte necoliniare (afin independente). Subspatiul afin p E generat de punctele M0,
M1, M2 are ca spatiu vectorial director un subspatiu de dimensiune doi in spatiul vectorial V3,
dat de
V2 =
Un punct M I p daca si numai
daca 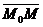 I
V2. I
V2.
Daca notam cu 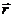 = =  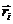 = = 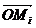 , i
= 0, 1, 2 vectori de pozitie ai punctelor M si respectiv M0,
M1, M2 in reperul cartezian R (O; , i
= 0, 1, 2 vectori de pozitie ai punctelor M si respectiv M0,
M1, M2 in reperul cartezian R (O; 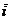  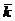 ),
(Oxyz) atunci multimea
punctelor planului p va fi caracterizat de
relatia vectoriala ),
(Oxyz) atunci multimea
punctelor planului p va fi caracterizat de
relatia vectoriala
 l, m I R (1.1) l, m I R (1.1)
numita ecuatia
vectoriala a planului prin trei puncte.
Daca (x, y, z), (xi, yi, zi) I R , i = 0, 1, 2 sunt
coordonatele punctelor M si
respectiv Mi, i = 0, 1, 2 atunci ecuatia
vectoriala (1.1) scrisa in reperul cartezian Oxyz este echivalenta cu ecuatiile
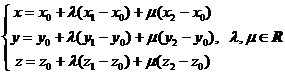 (1.2) (1.2)
numite ecuatiile
carteziene parametrice ale planului prin trei puncte.
Relatia  l l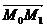 m m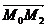 reprezinta conditia de coplanaritate a vectorilor
reprezinta conditia de coplanaritate a vectorilor 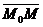  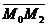 echivalenta cu anularea produsului
mixt, adica echivalenta cu anularea produsului
mixt, adica
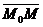  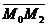 )
= 0 sau ( )
= 0 sau (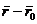   (1.3) (1.3)
In coordonate carteziene
ecuatia (1.3) se scrie sub forma
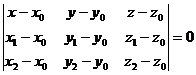 sau sau 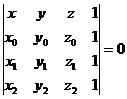 (1.4) (1.4)
numita ecuatie
carteziana a planului prin trei puncte.
In particular, punctele A (a,
0, 0), B (0, b, 0), C (0, 0, c) situate pe axele de coordonate ale
reperului Oxyz determina un
plan p, iar coordonatele punctelor
sale satisfac ecuatia
 , sau dupa
dezvoltare , sau dupa
dezvoltare
 (1.5) (1.5)
numita ecuatia prin taieturi a planului p
Remarca. Conditia
necesara si suficienta pentru ca patru puncte Mi(xi,yi, zi), 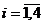 sa fie situate intr-un plan este sa fie situate intr-un plan este
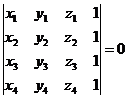 (1.6) (1.6)
1.2.
Planul printr-un punct, paralel cu doua directii date
Fie punctul M0 I E si dreptele distincte d1,
d2 E . Consideram in punctul M0 reprezentantii vectorilor  (l1, m1, n1)
, (l1, m1, n1)
, 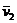 (l2, m2, n2)
paraleli dreptelor d1
respectiv d2 (fig.2) (l2, m2, n2)
paraleli dreptelor d1
respectiv d2 (fig.2)
Vectorii  si si 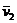 ,
liniar independenti genereaza subspatiul vectorial ,
liniar independenti genereaza subspatiul vectorial
V2 = .
fig.2
Punctul M0 I E si subspatiul vectorial V2 determina
subspatiul afin bidimensional p E . Un punct M I p daca si numai
daca 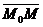 I
V2, adica vectorii I
V2, adica vectorii 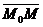  si si 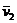 sunt coplanari. sunt coplanari.
Utilizand vectorii de
pozitie 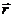 si si  corespunzatori punctelor M si respectiv M0, relatia de
coplanaritate corespunzatori punctelor M si respectiv M0, relatia de
coplanaritate 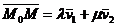 se scrie sub forma se scrie sub forma
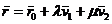 (1.7) (1.7)
numita ecuatia vectoriala a planului printr-un punct, paralel
cu doua directii.
Proiectand ecuatia
(1.7) pe axele sistemului cartezian de coordonate Oxyz obtinem:
|
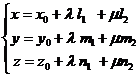
|
l m I R
|
|
numite
ecuatiile carteziene sub
forma parametrica ale planului printr-un punct, paralel cu
doua directii.
Relatia de coplanaritate a vectorilor 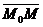 , ,  si si 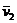 este caracterizata de anularea produsului mixt al celor trei vectori, adica ( este caracterizata de anularea produsului mixt al celor trei vectori, adica ( , ,  , ,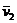 ) = 0. Obtinem astfel ecuatia ) = 0. Obtinem astfel ecuatia
 (1.9) (1.9)
numita ecuatia
carteziana a planului printr-un punct, paralel cu doua
directii.
Remarca. In particular,
ecuatia (1.9) poate fi adaptata si pentru alte situatii
cunoscute din geometria elementara, in care un plan este perfect
determinat. Anume: planul determinat de o dreapta si un punct nesituat
pe dreapta, planul determinat de doua drepte concurente si
respectiv planul determinat de doua drepte paralele.
Dreapta ca intersectie a doua plane
Se stie din
geometria elementara ca doua plane neparalele se
intersecteaza dupa o dreapta (d). In paragraful precedent aceasta situatie
geometrica este caracterizata analitic de un sistem de ecuatii
liniare compatibil nedeterminat, format cu ecuatiile celor doua
plane. Astfel, ecuatiile sistemului
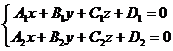 (2.7) (2.7)
vor fi numite ecuatiile
dreptei (d) data de
intersectia a doua plane.
O solutie (x0, y0, z0)
a sistemului (2.7) va caracteriza un punct al dreptei (d) iar vectorul  ,
unde ,
unde 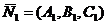 si si  sunt normalele celor doua plane ce
determina dreapta (d). sunt normalele celor doua plane ce
determina dreapta (d).
Observatie :
Ecuatiile carteziene (2.3) si
(2.6) ale unei drepte in spatiu pot fi interpretate ca un sistem de
doua ecuatii liniare, adica dreapta (d) gandita ca intersectia a doua plane.
|