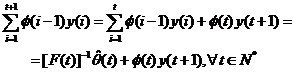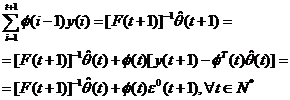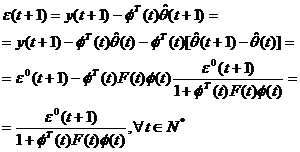Algoritm de identificare de tipul Celor Mai Mici Patrate, Recursiv (CMMPR)

Algoritm de identificare de tipul celor mai mici patrate, Recursiv (CMMPR)

Folosind algoritmul gradientului, minimizam la fiecare pas patratul erorii de predictie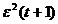, adica ne deplasam dupa cea mai rapida directie de descrestere a criteriului J din (3.16) cu un pas dependent de F. Minimizarea lui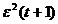la fiecare pas, nu presupune neaparat minimizarea unui criteriu de forma:

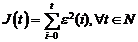    (3.25)

intr-un interval de timp de t pasi.

In vecinatatea solutiei optime, daca amplificarea algoritmului (lungimea pasului de avans) nu este convenabila, putem avea oscilatii in jurul punctului de minim. Pe de alta parte, pentru a avea o viteza buna de convergenta, atunci cand algoritmul lucreaza in faza initiala de cautare, departe de optim, ar fi de preferat sa avem o amplificare mare de adaptare. Algoritmul celor mai mici patrate recursiv asigura in fapt un profil de variatie a amplificarii de adaptare, astfel incat pe masura ce algoritmul de minimizare avanseaza, amplificarea (pasul de avans) scade in mod progresiv.

Consideram aceleasi ecuatii pentru proces, modelul de predictie si erorile de predictie folosite in algoritmul gradientului.

Scopul este de a gasi un algoritm recursiv de forma ecuatiei (3.9), folosind o matrice a amplificarii de adaptare F, ajustabila. Acest tip de algoritm minimizeaza criteriul de mai jos:

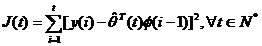(3.26)

Intr-o prima etapa, este vorba despre estimarea vectorului parametrilor la momentul t, pentru a minimiza suma patratelor abaterilor  intre proces si modelul de predictie intr-un interval de timp corespunzator unui numar de t masuratori. Valoarea lui 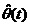care minimizeaza criteriul (3.26) se obtine cautand valoarea care anuleaza 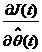, astfel:

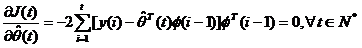(3.27)

Din ecuatia (3.27) se obtine:

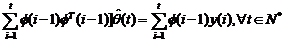(3.28)

Multiplicand la stanga cei doi termeni ai acestei ecuatii cu cantitatea 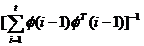, rezulta:

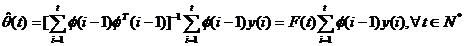  (3.29)

sau:

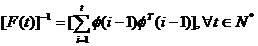(3.30)

Acest algoritm de estimare nu este recursiv. Pentru a obtine o varianta recursiva, consideram si estimatia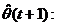

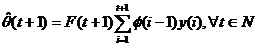(3.31)

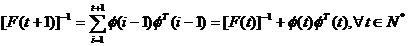(3.32)

Incercam o exprimare in functie de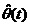

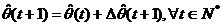(3.33)

Din ecuatia (3.31), avem:

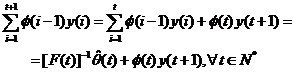
Tinand cont de ecuatiile (3.29) si (3.31), ecuatia (3.34) se poate scrie:

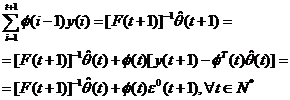    (3.35)

Multiplicand la stanga cu F (t+1), rezulta

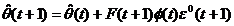, tIN^*    (3.36)

Algoritmul de estimare CMMPR din ecuatia (3.36) are o forma similara algoritmului gradientului dat in ecuatia (3.15), cu diferenta ca matricea de amplificare F este acum variabila in timp, pentru faptul ca ea depinde de masuratori (corecteaza automat directia gradientului si lungimea pasului de avans). Ramane de gasit o formula recursiva pentru F(t+1) plecand de la formula recursiva pentru F^-1(t+1) data in ecuatia (3.32). Aceasta se obtine folosind lema de inversiune matriciala cunoscuta, care pentru o matrice F patratica, de dimensiune (nxn) si un vector de dimensiune n, conduce la relatia:

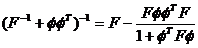(3.37)

Obtinem din ecuatiile (3.32) si (3.37), rezultatul:

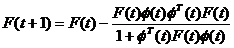tIN^* (3.38)

si regrupand relatiile obtinute anterior, dam o prima formulare a algoritmului de adaptare parametrica AAP pentru metoda celor mai mici patrate recursiva CMMPR:

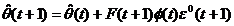tIN; (3.39)

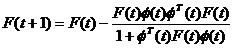tIN;   (3.40)

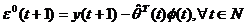(3.41)

O forma echivalenta de exprimare a acestui algoritm se obtine introducand expresia lui F(t+1) data ecuatia (3.40), in ecuatia (3.39). Obtinem astfel:

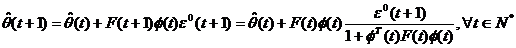(3.42)

Dar, din ecuatiile (3.7) si (3.8) avem:

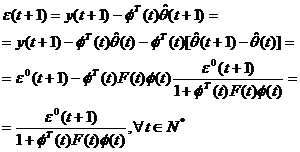(3.43)

adica relatia intre eroarea de predictie a posteriori si eroarea de predictie a priori. Folosind aceasta relatie in ecuatia (3.42) obtinem o exprimare finala a algoritmului de adaptare parametrica in conformitate cu metoda celor mai mici patrate recursiva:

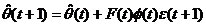, tIN;    (3.44)

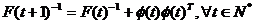  (3.45)

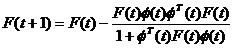, tI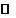; (3.46)

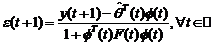  (3.47)

In practica, demaram algoritmul la t=0, punand:

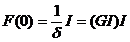, 0<d<<1,  (3.48)

O valoare tipica pentru d este d=0.001 (si deci amplificarea initiala, GI = 1000). Putem sa constatam pe expresia [F(t+1)]^-1 data de ecuatia (3.32), ca amplificarea de adaptare F, in acest caz, descreste in timp. O analiza riguroasa (pornind de la teoria de stabilitate a algoritmului) demonstreaza ca pentru toate initializarile cu matricea F(0) definite pozitiv, (F(0)>0),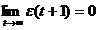

Algoritmul celor mai mici patrate recursiv CMMPR, este deci un algoritm de identificare cu amplificare de adaptare descrescatoare (pas de avans descrescator, ceea ce ii confera stabilitate in procesul de minimizare). Aceasta observatie se vede foarte clar daca consideram estimarea unui singur parametru. In acest caz F(t+1) si 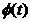sunt scalari, iar relatia (3.46) devine:

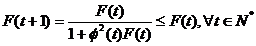
Algoritmul celor mai mici patrate recursiv acorda de fapt din ce in ce mai putina greutate noilor erori de predictie, deci noilor masuratori.

In consecinta, acest tip de variatie descrescatoare a amplificarii de adaptare nu va conveni pentru estimarea parametrilor variabili in timp. Trebuie sa fie considerate astfel si alte profile de variatie pentru amplificarea de adaptare.